关于一类广义半无限向量分式规划的对偶性研究

李　钰, 严建军, 李江荣

(1.延安大学 数学与计算机科学学院，陕西 延安 716000；2.延安职业技术学院，陕西 延安 716000)



关于一类广义半无限向量分式规划的对偶性研究

李钰1*, 严建军1,2, 李江荣1

(1.延安大学 数学与计算机科学学院，陕西 延安 716000；2.延安职业技术学院，陕西 延安 716000)

利用(F,α,ρ,d)K-V-凸性定义，讨论了一类广义半无限向量分式规划的对偶结果。

广义半无限向量分式规划； (F,α,ρ,d)K-V-凸函数；对偶；弱对偶

近些年，关于凸性理论，已有很多文献进行了研究。文献[1]引入了(F,ρ)-凸函数，文献[2]对之进行了推广，建立了广义的(F,ρ)-凸函数。文献[3]建立了更为广义的凸性条件，提出(F,α,ρ,d)-凸函数。文献[4]在(F,α,ρ,d)-凸性条件下研究了非光滑多目标分式规划问题的对偶定理。

作者利用文献[5]和[6]中广义(F,α,ρ,d)K-V-凸性定义，建立了半无限向量分式规划(FP)的Lagrange型对偶模型(FD)，得到了一类广义半无限向量分式规划的弱对偶定理。

1　预备知识和基本概念

定义1.2称泛函F:Rn×Rn×Rm→R是次线性的,如果对∀x1,x2∈Rn,有

(i)F(x1,x2;a1+a2)≤F(x1,x2;a1)+F(x1,x2;a2),∀a1,a2∈Rm;

(ii)F(x1,x2;ra)=rF(x1,x2;a),∀a∈Rm,r∈R,r≥0。

定义1.3[8]映射K:2X×X→2X称为局部渐近锥, 若对每一个集M⊆X和每一点x∈X,锥K(M,x)具有以下性质:

(i)K(M,x)=K(M-x,0);

(iv)K(M,x)=M, 对∀x∈intM;

(v)K(φ(M),φ(x))=φ(K(M,x)),这里φ:X→X为任一线性同胚;

(vi)O+M⊆O+K(M,x)。

我们已经提出了如下的定义[6]：

定义1.4设f是定义在非空开集X⊂Rn上的实向量函数,f:X→Rp,其每个分量fi是局部Lipschitz连续的,如果∃F:X×X×Rn→R是次线性函数,函数α=(α1,…,αp)Τ,αi:X×X→R+{0},d:X×X→R,ρ=(ρ1,…,ρp)Τ,ρi∈R和局部渐近锥K,如果对于∀x∈X,有fi(x)-fi(x0)≥F(x,x0;αi(x,x0)ξi)+ρid2(x,x0),∀ξi∈∂Kfi(x0),i=1,…,p,

则称f=(f1,…,fp)在x0∈X处是(F,α,ρ,d)K-V-凸的。

定义1.5设f是定义在非空开集X⊂Rn上的实向量函数,f:X→Rp,其每个分量fi是局部Lipschitz连续的,如果∃F:X×X×Rn→R是次线性函数,函数α=(α1,…,αp)Τ,αi:X×X→R+{0},d:X×X→R,ρ=(ρ1,…,ρp)Τ,ρi∈R和局部渐近锥K,如果对于∀x∈X,有

fi(x)-fi(x0)<0

⟹F(x,x0;αi(x,x0)ξi)+ρid2(x,x0)<0,

∀ξi∈∂Kfi(x0),i=1,…,p,

则称f=(f1,…,fp)在x0∈X处是(F,α,ρ,d)K-V-伪凸的。

定义1.6设f是定义在非空开集X⊂Rn上的实向量函数,f:X→Rp,其每个分量fi是局部Lipschitz连续的,如果∃F:X×X×Rn→R是次线性函数,函数α=(α1,…,αp)Τ,αi:X×X→R+{0},d:X×X→R,ρ=(ρ1,…,ρp)Τ,ρi∈R和局部渐近锥K,如果对于∀x∈X,x≠x0有

fi(x)-fi(x0)≤0

⟹F(x,x0;αi(x,x0)ξi)+ρid2(x,x0)<0,

∀ξi∈∂Kfi(x0),i=1,…,p,

则称f=(f1,…,fp)在x0∈X处是(F,α,ρ,d)K-V-严格伪凸的。

定义1.7设f是定义在非空开集X⊂Rn上的实向量函数,f:X→Rp,其每个分量fi是局部Lipschitz连续的,如果∃F:X×X×Rn→R是次线性函数,函数α=(α1,…,αp)Τ,αi:X×X→R+{0},d:X×X→R,ρ=(ρ1,…,ρp)Τ,ρi∈R和局部渐近锥K,如果对于∀x∈X,有

fi(x)-fi(x0)≤0

⟹F(x,x0;αi(x,x0)ξi)+ρid2(x,x0)≤0,

∀ξi∈∂Kfi(x0),i=1,…,p,

则称f=(f1,…,fp)在x0∈X处是(F,α,ρ,d)K-V-拟凸的。

对于半无限向量分式规划:

s.t.hj(x)≤0,j∈J,

考虑其Lagrange型对偶规划

(FD)maxG(y,μ)=

(μj)j∈J≥0,对一切j∈J,且仅有有限个μj≠0。

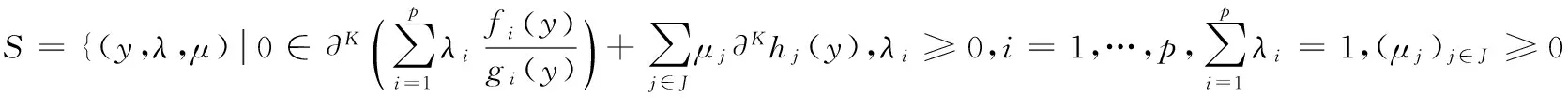
2　对偶定理定理

(ii)对于j∈J(y),h在y处是(F,β,ρ2,d)K-V-凸函数;

(iii)μjhj(y)=0,j∈J;

(iv)广义Slater条件成立,即∃x0∈X,满足hj0(x0)<0,j0∈J(y),且相应的μj0>0;

(v)α1=…=αp=β1=…=β(J)=δ;

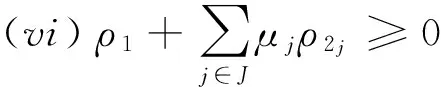
且至少∃i0,1≤i0≤p,i≠i0,使得

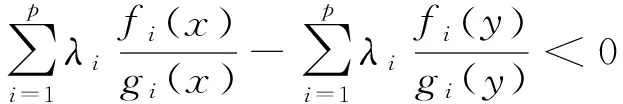
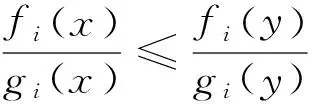
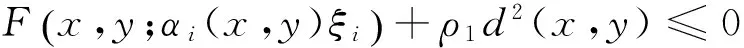
(1)

又由于hj0(x)<0=hj0(y),j0∈J(y),有hj0(x)-hj0(y)<0。

由(ii)知

F(x,y;βj0(x,y)ζj0)+ρ2j0d2(x,y)<0,

∀ζj0∈∂Khj0(y),

由μj0>0,可得

F(x,y;βj0(x,y)μj0ζj0)+μj0ρ2j0d2(x,y)<0,

∀ζj0∈∂Khj0(y),

(2)

因μj≥0,j∈J(y),hj(y)=0,有

μjhj(y)≥0,

则hj(x)≤0≤hj(y)。

又由(ii)知, 对于∀ζj∈∂Khj(y),有

F(x,y;β(x,y)μjζj)+μjρ2jd2(x,y)≤0,

j∈J(y),j≠j0,

对上式中j∈J(y)且j≠j0求和,得

(3)

当j∈JJ(y)时,取μj=0, 则有

(4)

式(1)+(2)+(3)+(4),并利用F的次线性性质和(v),可得

这与(FD)的第一个约束条件矛盾！故

(ii)对于j∈J(y),h在y处是(F,β,ρ2,d)K-V-拟凸函数;

(iii)μjhj(y)=0,j∈J;

(iv)α1=…=αp=β1=…=β(J)=δ;

且至少∃i0,1≤i0≤p,i≠i0,使得

由(iii)和(i)得

(5)

又因hj(x)≤0=hj(y),j∈J(y)和(ii),知

F(x,y;βj(x,y)ζj)+ρ2jd2(x,y)≤0,

∀ζj∈∂Khj(y),j∈J(y),

则由μj≥0,有

F(x,y;βj(x,y)μjζj)+μjρ2jd2(x,y)≤0,

∀ζj∈∂Khj(y),j∈J(y),

当j∈JJ(y)时,取μj=0, 则有

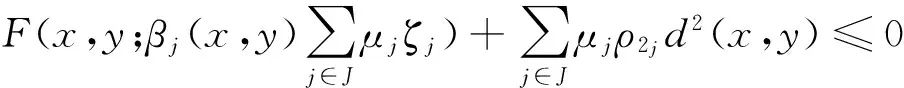
∀ζj∈∂Khj(y)

(6)

式(5)+(6),并利用F的次线性性质以及(iv)、(v),可得

这与(FD)的第一个约束条件矛盾！故

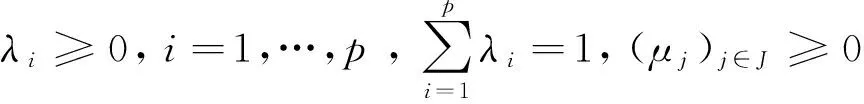
(ii)对于j∈J(y),h在y处是(F,β,ρ2,d)K-V-拟凸函数;

(iii)μjhj(y)=0,j∈J;

(iv)α1=…=αp=β1=…=β(J)=δ;

证明与定理2.2的证明类似。

[1]PredaV.Onefficiencyanddualityformultiobjectiveprograms[J].JournalofMathematicalAnalysisandApplications, 1992, 166:365-377.

[2]XUZ.Mixedtypedualityinmultiobjectiveprogramming[J].JournalofMathematicalAnalysisandApplications,1996,198:621-635.

[3]LIANGZA,HUANGHX,PardalosPM.Optimalityconditionsanddualityforaclassofnonlinearfractionalprogrammingproblems[J].JournalofOptimizationTheoryandApplication, 2001,110(3):611-619.

[4] 姚元金.(F,α,ρ,d)-凸性下的非光滑多目标分式规划问题的对偶[J]. 湖北民族学院学报(自然科学版), 2014,32(2):124-127.

[5] 李钰,张庆祥,严建军,等. (F,α,ρ,d)K-V-凸半无限分式规划的最优性条件[J]. 江西科学, 2009,27(1):31-35.

[6] 李钰,张庆祥,严建军,等. 一类广义半无限分式规划的最优性条件[J]. 河南科学, 2009,27(2):132-136.

[7]ClarkeFH.Optimizationandnonsmoothanalysis[M].NewYork:JohnWiley&Sons,Inc., 1983.

[8]ElsterKH,ThierfelderJ.Onconeapproximationsandgeneralizeddirectionalderivatives[M]//ClarkeFH,DemyanovVF,GiannessiF.Nonsmoothoptimizationandrelatedtopics.NewYork:SpringerUS,1989:133-154.

[9]ShimizuK,IshizukaY,BardJE.Nondifferentiableandtwo-levelmathematicalprogramming[M].Boston:KluwerAcademic,1997.

[10]Marcocastellani.Nonsmoothinvexfunctionsandsufficientoptimalityconditions[J].JournalofMathematicalAnalysisandApplications, 2001,255(1):319-332.

[11]LIUJC.Optimalityanddualityforgeneralizedfractionalprogramminginvolvingnonsmoothpseudoinvexfunction[J].JournalofMathematicalAnalysisandApplication, 1996(220):667-685.

[12]胡毓达,孟志青. 凸分析与非光滑分析[M]. 上海:上海科技出版社, 2000.

[13]卢厚佐,高英. 多目标分式规划逆对偶研究[J]. 数学的实践与认识, 2014,44(23):172-178.

[14]李钰,严建军,李江荣. 具有广义凸性的一类半无限向量分式规划的鞍点准则[J]. 贵州大学学报(自然科学版), 2015,32(5):1-4.

(责任编辑：周晓南)

Duality for a Class of Generalized Semi-infinite Vector Fractional Programming

LI Yu1*, YAN Jianjun1,2, LI Jiangrong1

(1.College of Mathematics and Computer Science, Yan’an University, Yan’an 716000, China;2.Yan’an Vocational and Technical College, Yan’an 716000, China)

Some duality theorems based on the definition of the(F，α，p，d)k-V-convex function for a class of generalized semi-infinite vector fractional programming were studied.

generalized semi-infinite vector fractional programming;(F，α，p，d)k-V-convex function; duality; weak duality

1000-5269(2016)02-0006-04

10.15958/j.cnki.gdxbzrb.2016.02.02

2015-11-06

国家自然科学基金项目资助(11471007)；陕西省高水平大学专项资金项目资助(2012SXTS07) ；陕西省教育厅科研计划项目资助(14JK1827)；延安市科技计划项目资助(2014KG-05)；延安大学科研基金项目资助(YD2011-09)

李钰(1982-)，女，讲师，研究方向：运筹学、最优化理论、算法与应用，Email:jsjxy419@126.com.

李钰, Email:jsjxy419@126.com.

O221.6

A