基于Al-Cu-Li合金流变行为的动态再结晶动力学与形核机制

杨胜利，沈 健，闫晓东，李锡武，孙宝庆，毛柏平



基于Al-Cu-Li合金流变行为的动态再结晶动力学与形核机制

杨胜利1, 2，沈 健1，闫晓东2，李锡武1，孙宝庆2，毛柏平1

(1. 北京有色金属研究总院 有色金属材料制备加工国家重点实验室，北京 100088；2. 北京有色金属研究总院 有色金属加工中心，北京 100088)

对Al-Cu-Li合金进行温度300~500 ℃、应变速率0.001~10 s−1的等温热压缩，分析合金的流变行为；结合TEM和EBSD研究合金热变形过程中的组织演变。结果表明：合金流变曲线分为3个阶段：加工硬化阶段、过渡阶段和稳态变形阶段；变形温度越高，流变应力达到动态平衡所需应变量越小。基于应变硬化率()与流变应力()之间的关系，确定动态再结晶的临界应变(c)；不同热变形条件下的临界应变(c)与峰值应变(p)之比为0.30342~0.92828；临界应力(c)与峰值应变(p)之比为0.88492~0.99782。引入最大软化率应变(*)和中间变量/，建立c和*与/的关系表达式。构建Al-Cu-Li合金动态再结晶动力学模型，模型表明，温度越高或应变速率越低，越有利于促进动态再结晶分数的增加；显微组织分析结果与模型预测规律一致。Al-Cu-Li合金动态再结晶形核机制主要为晶界突出形核机制、亚晶合并长大机制以及粒子促进形核机制，随温度升高和应变速率的降低，晶内亚晶合并长大机制得到加强。

Al-Cu-Li合金；临界应变；动态再结晶模型；再结晶形核机制

铝锂合金因其低密度、弹性模量高、比强度和比刚度高、良好的抗损伤性等特点在航空航天领域得到广泛应用[1−3]。Al-Cu-Li合金作为第三代铝锂合金，减少Li元素的含量，从而改善其热加工性，并减弱了合金的各向异性[4−5]。热加工过程中产生的动态再结晶影响合金显微组织演化和宏观力学性能[6]。研究不同变形条件下合金的动态再结晶动力学和形核机制对合金最终组织性能的控制具有重要意义。国内外针对铝合金动态再结晶行为的研究已有诸多报道，陈学海等[7]采用线性回归方法建立了7085铝合金的动态再结晶动力学方程，并采用金相测定法建立其峰值应变方程和临界应变方程；郭海龙等[8]运用统计回归的方法建立了挤压态7050合金的动态再结晶经验模型，最终获得加载路径对工件晶粒尺寸特性的影响规律。杨栋 等[9]依据唯象理论的指数模型，采用线性回归法获得了7075合金热变形过程的动态再结晶晶粒度演化模型。CHO等[10]研究了Al-5%Mg(质量分数)合金热变形行为与动态再结晶，把应变、应变速率和温度用Zener-Hollomon参数定量表达，从而构建合金的动态再结晶模型。MOMENI等[11]基于亚晶尺寸演化构建了合金不连续动态再结晶过程中新晶粒的形核与长大模型，该模型为研究动态再结晶过程中显微组织的演化提供了理论支持。张飞等[3]研究了2099铝锂合金热变形过程中的动态软化机制，分析了不同Z值条件下合金的动态软化行为。但多数研究主要集中在不同合金的本构行为和相应组织演化分析，而对Al-Cu-Li合金动态再结晶的临界条件和动态再结晶形核机制的研究却鲜有报道。合金开始产生动态再结晶所对应应变称为临界应变，该应变是判断是否发生再结晶的主要依据，对热加工变形具有重要意义。真应力−应变曲线反映合金在塑性变形过程中的组织演化[12]，拟合流变曲线中反映合金显微组织状态的潜在条件，构建动态再结晶模型，可以减小主观因素影响，准确反映合金组织演化规律。

本文作者基于Al-Cu-Li合金的真应力­­−应变曲线，结合应变硬化率()与流变应力()之间的关系，确定流变曲线的特征点：动态再结晶临界应变(c)；峰值应力(p)；最大软化率应变(*)。利用变形参数和设计的中间变量(/)，建立变形条件与动态再结晶分数之间的动力学关系模型；对变形组织进行TEM和EBSD分析，验证动力学模型，讨论Al-Cu-Li合金热变形过程的动态再结晶形核机制。

1 实验

实验材料为由国内某铝业公司提供的铝锂合金半连续铸锭，其化学组成如下：Cu 2.42，Li 1.49，Mn 0.28，Mg 0.032，Ti 0.026，Zr 0.092，Si 0.015，Al 余量(质量分数，%)。热压缩实验前对合金进行(460 ℃, 20 h)+ (525 ℃, 24 h)均匀化处理，消除枝晶偏析。热压缩试验在Gleeble−1500型热模拟机上进行，试样规格为10 mm×15 mm，试样与压头接触面采用石墨润滑以减小摩擦。变形温度为：300~500 ℃，间隔温度40 ℃；压缩变形量为60%；应变速率()分别如下：10、1、0.1、0.01和0.001 s−1。以5 ℃/s的升温速率升至变形温度后，保温3 min消除温度梯度；压缩方向与铸锭厚度方向一致，热变形完成后立即用水冷却，保留合金高温变形组织。水冷试样沿压缩方向对称切开，经砂纸打磨后进行电解抛光，电解液成分为酒精和高氯酸(体积比9:1)，参数为20 V/12 s，之后进行EBSD分析。透射试样经机械减薄至50 μm，后采用体积比1:3的硝酸甲醇溶解双喷减薄，双喷参数如下：−30 ℃、55~60 mA。

2 结果与讨论

2.1 流变行为分析

图1所示为试验合金在不同变形温度和应变速率下的真应力−应变曲线。由图1可以看出，不同变形条件下，流变应力先快速增加至峰值，而后逐渐趋于稳定，预示合金动态再结晶的发生和由此引起的应变硬化率的变化[12]。流变应力变化的实质是位错的增殖与消减以及由动态再结晶引起的组织演化。图1中所示的流变曲线变化可分为3个阶段[13]：加工硬化阶段、过渡阶段和稳态变形阶段。加工硬化阶段，随应变增加，位错快速增殖，位错间的交互作用也增加其运动阻力，导致流变应力急剧增加，当达到动态再结晶所需临界值，出现动态再结晶。应变进一步增加，动态回复和动态再结晶程度逐渐增加，流变应力增速减缓，达到峰值后逐渐下降。当加工硬化和动态软化达到动态平衡，流变应力进入稳定阶段。由不同温度下流变曲线可以看出，当温度高于380 ℃(420~500 ℃，=0.001~10 s−1)，过渡阶段不明显，因变形参数中的变形温度对流变应力的影响高度显著[14]。随温度升高，动态回复与再结晶程度增加，更高的动态软化率致使加工硬化和动态软化在更小的应变程度达到动态平衡阶段，即变形温度越高，流变应力达到动态平衡所需的应变量越小。

图1 不同应变速率下Al-Cu-Li合金的真应力­­−真应变曲线

2.2 动态再结晶临界条件表征

临界应变(c)是表征动态再结晶开启与演变过程的重要参数之一，准确描述变形条件对临界应变的影响规律是建立动态再结晶动力学模型的关键。通过金相组织观察确定合金动态再结晶开始的临界应变比较困难，需要大量分析动态再结晶前后的组织变化。通常采用POLIAK等[15]提出的应变硬化率(=d/d)和流变应力()关系曲线的拐点确定动态再结晶临界点，该方法以峰值应力为上限，通过−的三次多项式拟合经二阶求导后确定临界应变。图2所示为Al-Cu-Li合金不同变形条件下合金的−曲线，由图2(a)和(b)可以看出，部分变形条件下(见图2中未标示“□”的曲线) 应变硬化率的突变点并不明显，这可能是因为部分变形条件下−不符合三次多项式拟合关系，导致临界点的确定和计算出现误差。

图2 不同温度和应变速率下峰值应力前应变硬化率(θ)与流变应力(σ)的关系曲线

为更精确地确定动态再结晶的临界点，可通过(d/d)−和(d2/d2)−关系曲线方法确定[16]。以380 ℃、0.1 s−1变形条件下的流变曲线举例说明，图3(a)和(b)所示分别为该变形条件下合金的−和−曲线；图3(c)和(d)分别为(d/d)−和(d2/d2)−关系曲线。图3(b)所示的−曲线表明此变形条件下合金的应变硬化率()出现动态再结晶的拐点但不明显，通过(d/d)−(见图3(c))和(d2/d2)−(见图3(d))关系曲线可以看出，当应变超过一定值(见图3(d)中“□”所示) d2/d2值突变。将突变不明显的所有变形条件均采用上述方法确定动态再结晶临界点，结合POLIAK等提出的方法，可确定临界应变(c)和相应的临界应力(c)，最终确定不同变形条件下的临界应力与峰值应力比值、临界应变与峰值应变之间的关系：c/p= 0.30342~ 0.92828；c/p=0.88492~0.99782。

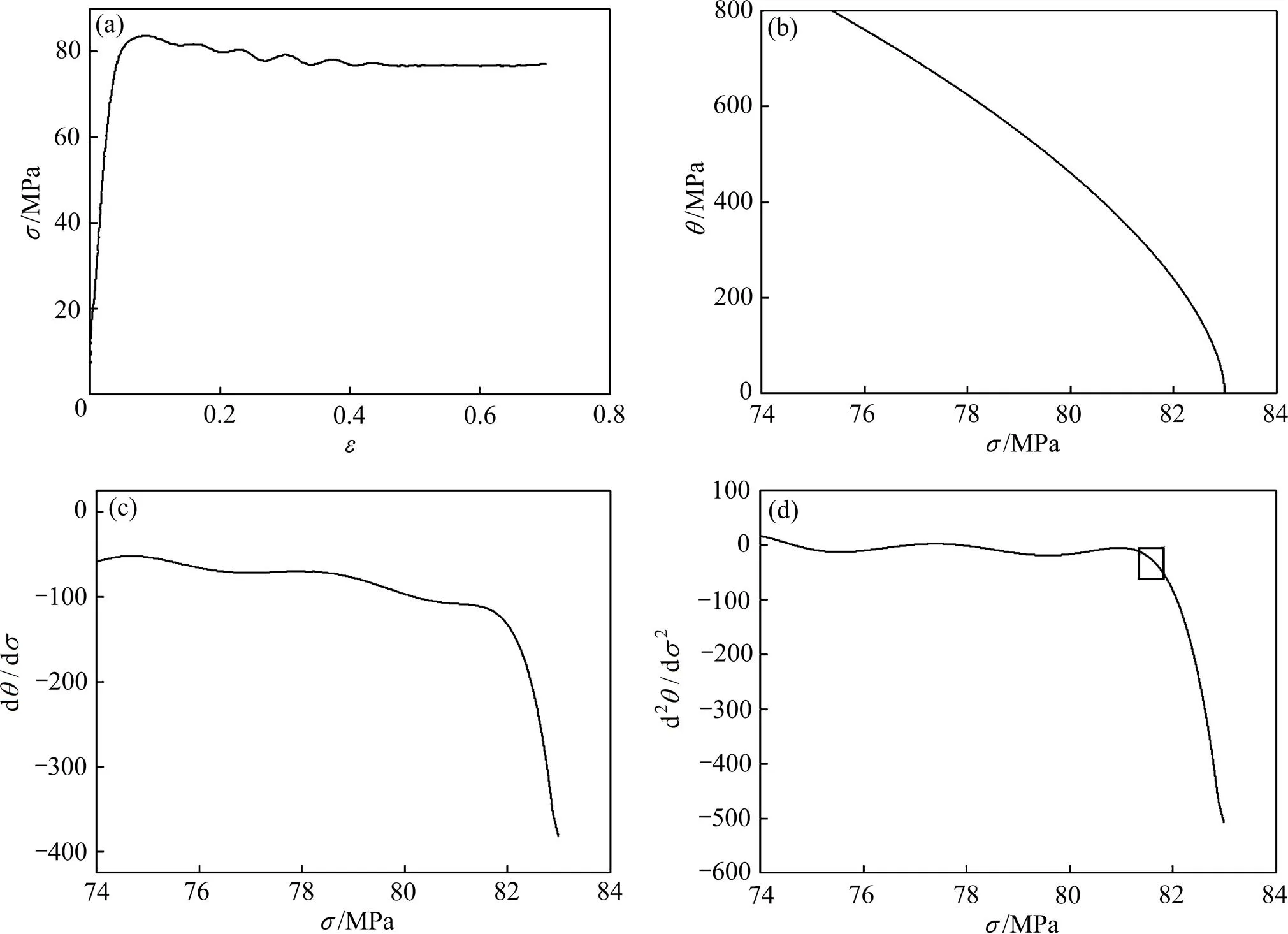
图3 Al-Cu-Li合金380 ℃、0.1 s−1变形条件下应变硬化率和流变应力之间的关系图

根据临界应变与Zener-Hollomon参数(=exp[/()]。其中，为变形激活能；为变形温度；为摩尔气体常数)之间的关系，可分析变形温度与应变速率对动态再结晶临界点的影响。如图4所示为lnc与ln间的关系曲线，通过线性回归分析得式(1)：

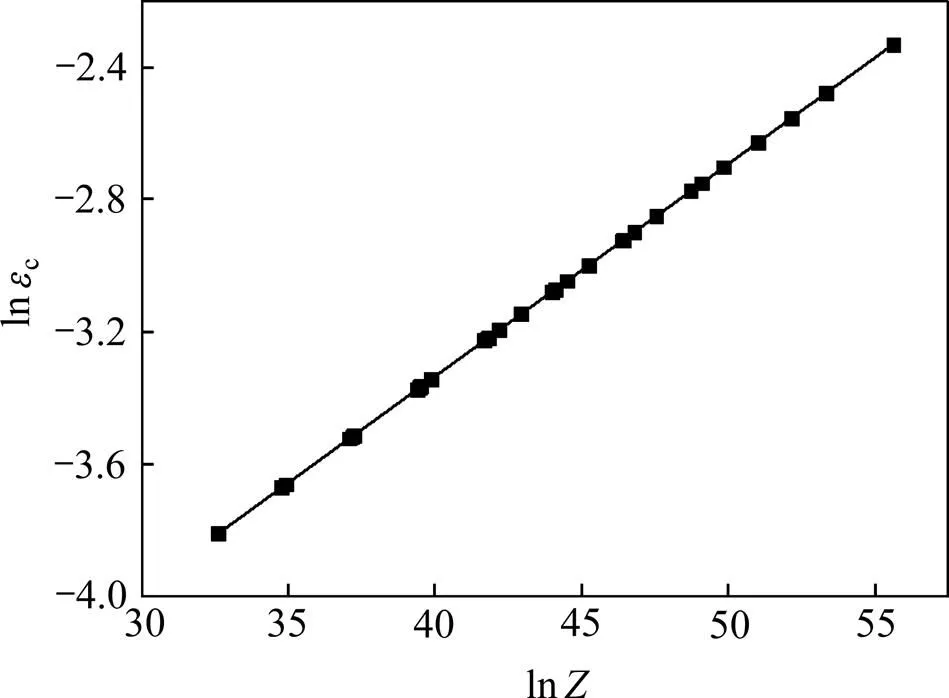
图4 临界应变与ln Z参数的关系

确定临界应变(c)与关系，如式(2)所示：

分析式(2)可知，临界应变对变形条件敏感，随变形温度的降低或应变速率的增加而增加。因为变形温度越高，合金原子的振幅越大，扩散速率越高，有助于促进刃型位错的攀移和螺位错的交滑移，有利于合金动态再结晶的产生，即减小临界应变。随着应变速率的增加，位错可运动的时间缩短，合金组织未能充分进行动态再结晶的形核与长大，不利于动态再结晶的软化作用，促使动态再结晶软化和应变硬化达到平衡所需的应变量增加[17]。

2.3 动态再结晶动力学模型

合金的动态再结晶的动力学模型常采用JMAK模型描述[18]，即动态再结晶体积分数表示为有关变形时间的函数，即：

式中：r为动态再结晶分数；为热处理时间；0.5为动态再结晶分数为50%对应的时间；为Arami指数。该模型需要在多个时间间隔条件下，经不同变形条件变形后快速冷却，然后统计分析不同时间间隔下合金的金相组织，计算合金的再结晶体积分数。统计结果受主观因素影响较大。本研究中通过结合合金流变行为，把模型中关于时间的参数用有关应变的函数代替，减小组织观察过程中主观因素的影响，则动态再结晶分数可用式(4)表示：

式中：为Avrami常数(1＜＜2)；c为临界应变；*为最大软化率对应的应变，可通过应变硬化率()的最小值确定，如图5所示。图5(a)、(b)所示分别为Al-Cu-Li合金在0.001 s−1和1 s−1不同温度变形的−曲线。由最小应变硬化率确定所有变形条件下的最大软化率应变(*)，结果如表1所列。由表1可以看出，应变速率一定时，随温度的升高，ε*不断减小；当温度一定，随应变速率的增加，*不断增加。设计中间变量：/，则临界应变(c)和最大软化率应变(*)与/的关系如图6所示，通过最小二乘法拟合可得式(5)和(6)：

为确定式(4)中的值，令不同变形条件下的r≈1，即流变应力进入稳定阶段，如图1所示，取应变为0.7，合金流变应力均进入稳定阶段，计算不同变形条件下的值，得平均值为1.031578，可确定Al-Cu-Li合金的动态再结晶动力学模型。结合式(4)、(5)、(6)可知，应变速率一定时，随着变形温度的升高动态再结晶体积分数逐渐增加，达到相同体积分数所需应变更小，时间更短。当温度为定值，随着应变速率的升高，达到相同动态再结晶体积分数所需应变更大，时间更长；当温度和应变速率确定，随着应变量的增加，合金的动态再结晶分数逐渐增加。

图5 不同变形条件下合金应变硬化率(θ)的最小值

图6 和与的关系