铝电解槽下料过程对电解质温度场的影响

丁培林，王 恒，黄 俊，王紫千，曹 斌



铝电解槽下料过程对电解质温度场的影响

丁培林1，王 恒1，黄 俊2，王紫千2，曹 斌2

(1. 华中科技大学 力学系，武汉 430074；2. 贵阳铝镁设计研究院有限公司 技术研发中心，贵阳 550081)

铝电解槽内保持良好的热平衡可以减少铝电解过程中的能耗，而氧化铝周期性的下料会破坏电解槽热平衡。建立铝电解槽电解质浓度−热场瞬态模型，在精确模拟氧化铝浓度分布的基础上，研究下料期间电解质温度及热平衡的变化趋势。结果表明：氧化铝下料时，电解质极距层局部温度降低5 ℃左右，上表面附近区域最多降低十几度；下料结束20 s内，逐渐恢复到正常温度；氧化铝下料会打破电解质内的热平衡，其中部分热量(最高达300 kW)用来加热氧化铝颗粒；20 s后，电解质会达到新的热平衡状态。

铝电解槽；氧化铝浓度分布；浓度；热场；热平衡

铝电解是高能耗工业，在氧化铝电解生成金属铝的过程中需要消耗大量的电能，同时，电流生成的热量维持电解所需要的温度。电解槽生产时，热量的生成区域主要集中在阳极与铝液间的极距层，极间生成的热量随着电解质的流动而散发，通过电解质与内衬界面的对流传热向内衬传递，再通过内衬材料的热传导向槽外表面传递[1]。电解质作为主要的产热源，其温度变化对全槽热平衡影响很大，因此，正确认识电解质温度场一直是铝电解行业亟待解决的重要课题。

实践证明，铝电解质温度的高低，与电流效率的高低有直接关系。电解质温度每降低10 ℃，电流效率将提高1%~1.5%。在下料过程，由于常温氧化铝的添加，会对电解槽原有的热平衡产生干扰；随着氧化铝下料的结束，氧化铝颗粒在流动电解质的带动下逐渐扩散到全槽，并被加热到电解温度950 ℃左右，然后达到新的热平衡状态[2]。在电解槽运行过程中，每隔几十秒就要打壳下料一次，这势必会频繁地改变电解质的温度场，进而打破电解槽的热平衡。因此，为了保持良好的热平衡，提高电流效率，迫切需要了解下料期间电解质的温度场的变化规律。

对于电解质温度场，不少学者已做了大量深入的研究，TABSH等[3]和DUPUIS等[4−5]采用ANSYS软件建立了电解槽的三维半槽和全槽模型，对400、500以及600 kA级大型电解槽进行了数值仿真研究。崔希凤等[6−7]采用ANSYS电−热场耦合模块计算了300 kA级电解槽3D槽帮形状，同时考察其温度分布以及各部分压降，计算结果与实际情况相符，但其只考虑了1/4槽的情况。对氧化铝颗粒在电解质中的扩散，有很多学者运用仿真软件对其进行了模拟研究。例如，THOMAS[8]对氧化铝颗粒的溶解过程进行了数值模拟，但其计算方法过于复杂，不便于工程应用。詹水清等[9]通过Fluent软件对铝电解槽内气液两相流多组分模型进行了数值计算，但他们采用氧化铝均一消耗模型。张翮辉等[10−12]通过CFX软件建立了420 kA和500 kA铝电解槽氧化铝输运过程的多组分多相流模型，并引入了涡结构分析方法来研究电解质流场和下料过程，但其计算时间较短，氧化铝浓度未呈现出周期性稳定变化。关于下料过程对电解质温度场的影响，国内外很少有人做过相关的研究。基于这些认识，本文作者结合电解质温度场、流场和氧化铝浓度场，建立电解质浓度−热场瞬态模型，采用仿真模拟手段来研究氧化铝下料对电解质温度场的影响。

为此，本文作者首先在ANSYS Workbench电−热场模块中建立了3D全槽电−热场模型，求解电解质热量及电解质底面电流分布；然后，在Maxwell平台上建立了电磁场模型，求解电解质区域的电磁力分布；

最后，基于CFD计算软件CFX，建立了电解质浓度−热场瞬态模型，分析研究下料过程中电解质温度场变化规律以及电解质热平衡状态的变化，旨在为铝电解槽生产设计提供技术指导。

1 电解质浓度−热场计算模型

1.1 模型简化

铝电解槽内的熔体流动及氧化铝扩散是一个复杂的过程，受很多因素的影响。为了方便对电解质进行计算模拟，对其简化是必要的。为此，本文作者做如下假设：1) 电解质视为由冰晶石和氧化铝两种组分组成的均相、不可压缩流体，且炉帮形状一定；2) 阳极底掌平整；3) 只考虑电解质层，忽略铝液层的存在；4) 阳极气体为直径不变的气体颗粒，气泡直径当量取为6 mm[13−14]。

1.2 电解质壁面传热及焦耳热

由于流体流速在壁面附近迅速下降并趋于0，因而近壁面区域的流动状况与流体主体有很大区别，一般采用壁函数对流体流动的边界层进行近似处理[15]。对于电解质与内衬的换热，采用牛顿表面冷却定律进行描述和计算，其形式如下：

式中：、b、w和f分别为热流密度、换热系数、表面温度和流体温度。

铝电解槽的电解质区域是铝电解槽中的主要产热源，其产热规律符合焦耳定律，发热功率按下式计算：

式中：为通过电解质的电流，A；为电解质电阻，Ω；为压降，V。

为了得到电解质产热效率，本文作者在ANSYS平台上建立了三维全槽电−热场模型，模型包括阳极部分、炉帮、覆盖料、保温内衬、电解质、铝液、阴极部分等，通过加载电流载荷和对流散热边界条件进行求解，然后根据式(2)提取每个单元内的焦耳热，最后求和得到整体电解质的产热效率为600 kW。

1.3 欧拉−欧拉非均相流模型及控制方程

均相流模型认为气液两相混合的很好，具有相同的流动速度和温度，但这与实际中的流动不符合。为此，本文作者基于欧拉−欧拉非均相多相流模型来描述电解质−气泡的两相流动。在模拟中，将电解质视作连续相；考虑到阳极气泡直径很小且体积分数很小，将阳极气泡视作离散相。

在模拟中，将电解质区域中的电解质定义为1相，气泡定义为2相，则控制电解质流场连续性方程和动量守恒方程分别为[10]

本文作者通过仿真软件MAXWELL建立铝电解槽的电磁场模型，求解得到了铝电解槽电解质区域的电场和磁场分布；然后，根据得到电解质区域内的电磁力的分布；在此基础上，采用CFX软件进行流场计算时，将电磁力以质量源项的方式进行加载。

1.4 氧化铝消耗与下料模型

基于李劼等[9−11]提出的电解质−铝液界面氧化铝发生还原反应的理论，本文作者在电解质−铝液界面上设置氧化铝消耗分布函数。为了保证氧化铝流入和消耗的平衡，通过氧化铝消耗函数计算得到氧化铝的消耗量，并将其作为氧化铝颗粒的下料量。

1) 氧化铝消耗模型

根据法拉第定律、氧化铝电解方程，氧化铝的质量消耗速率可表达为[10]

式中：loc为氧化铝的局部消耗速率；b为底面电流密度分布；为电化学当量；为电流效率。

由式(5)可知，电解质局部消耗速率loc和电流密度分布b有关，因此，本文作者在电磁场模型中提取底面电流密度分布，根据式(5)得到氧化铝消耗的分 布。然后根据消耗量及物料平衡计算出下料量约为 0.07 kg/s。

2) 氧化铝下料模型

氧化铝下料后，首先形成一个料堆漂浮在电解质表面，随后被阳极气泡击碎搅动，逐渐分散并没入电解质中。因此，本文作者认为氧化铝进入电解质有时间滞后性，且氧化铝溶入电解质相也需要一定的时间，假设为10 s。

为此，本文作者采用的基准周期为72 s，每个周期的下料量根据全槽氧化铝消耗量得到。假设下料点为6个(见图1)，按照工艺设计要求，下料期间6个点同时下料，氧化铝的扩散系数设为1.5×10−9m2/s。

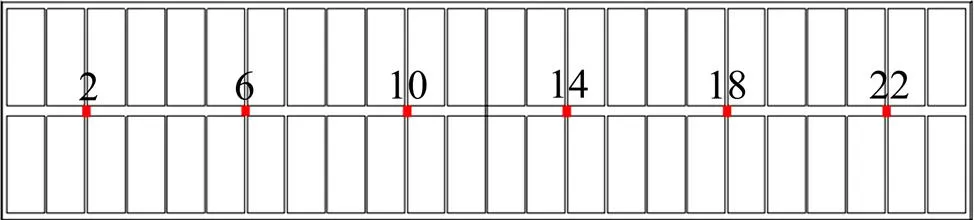
图1 铝电解槽下料点位置示意图

1.5 材料属性与边界条件

在热场和流场计算中，需要给定材料属性包括电解质和阳极气泡的密度、黏度、比热容、导热系数等。参考以前的研究工作[10, 16−18]，本研究中的材料属性设置如表1所列。

表1 铝电解槽流体相关物性参数

1) Heat.

为了瞬态计算收敛性，本文作者首先建立稳态电解质浓度−热场模型，并将稳态计算结果作为瞬态浓度−热场计算的初始条件，然后进行计算。在稳态模型计算时，舍去氧化铝下料、消耗边界，计算类型由瞬态改为稳态，初始流体域内电解质相的体积分数1=1，氧化铝占电解质比例为2.5%，气相的体积分数2=0，其他条件不变。

1.6 物理模型

本文作者以某420 kA铝电解槽作为研究对象，实现电解质浓度−热场模型的求解计算。在建模及计算过程中所需的基本结构与工艺参数如表3所示。

表3 某420kA铝电解槽工艺与结构参数

根据设计图纸在SolidWorks平台上建立电解质的物理模型，并在CFD ICEM上划分结构化网格，在阳极间缝、中缝等位置进行局部加密，网格数量约为30万，网格质量如图2。

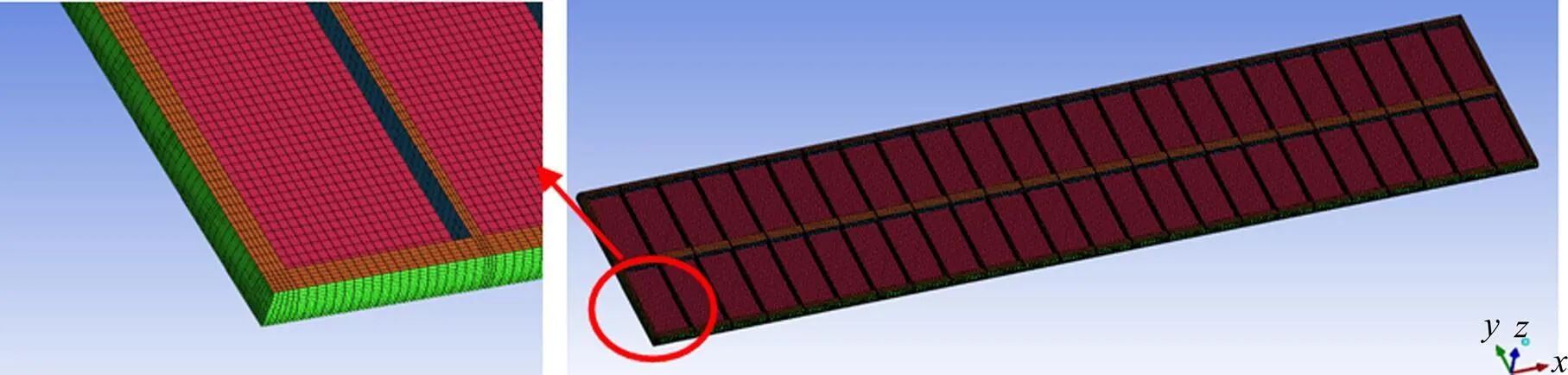
图2 420 kA电解质浓度−热场计算网格

2 结果与分析

2.1 电解质稳态浓度−热场模型结果分析

为了保证电解质瞬态浓度−热场模型的准确性，本文作者计算稳态结果作为瞬态模型的初始条件，提取稳态电解质温度场、流场及氧化铝浓度分布进行简单分析，如图3所示(面为极距中间截面)。由图3可以发现，电解质温度中间稍高、四周稍低，由于电解质的流动，整体温度分布比较均匀；在阳极炭块下方，温度有些许变化，这是阳极炭块底部产生阳极气体的原因。电解质区域的水平流速存在较大的差异，在阳极投影四周和槽子角部区域流速较大，且在小面附近形成两个漩涡，这与文献[10,18]结果一致。在稳态模型中，全槽氧化铝浓度为2.5%(质量分数)，并作为瞬态模型的初始浓度。

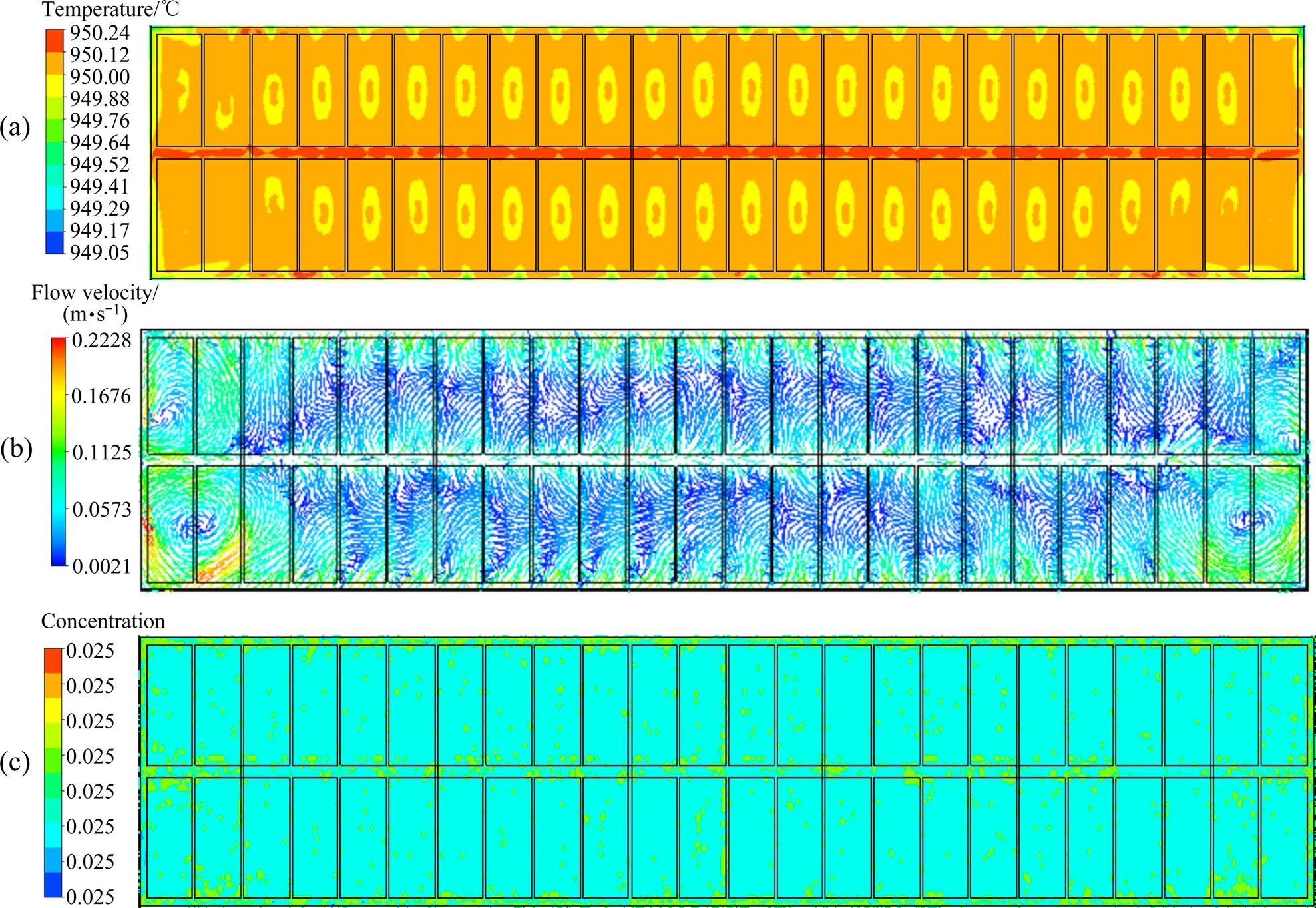
图3 稳态浓度−热场电解质区域XY面温度分布、流速分布及浓度分布图

2.2 氧化铝浓度分布及周期稳定性分析

在铝电解槽运行过程中，氧化铝浓度分布随着下料过程呈周期性变化，为了验证计算中氧化铝浓度场是否达到了周期性稳定变化状态，本文作者给出面氧化铝最大、最小浓度随时间变化曲线。由图4可以看出，随着氧化铝下料，其最大浓度由2.65%上升到3.65%，但随氧化铝的消耗，其浓度又逐渐降低到2.65%，且很快呈现出周期性稳定变化；最小浓度则由2.5%一直降低，在400 s(第5个周期)左右趋于平缓，并随下料周期的变化稍有波动。由最大、最小浓度可知，在400 s之后，氧化铝浓度场的计算结果已趋于稳定的周期性变化状态，可视作已达到收敛。

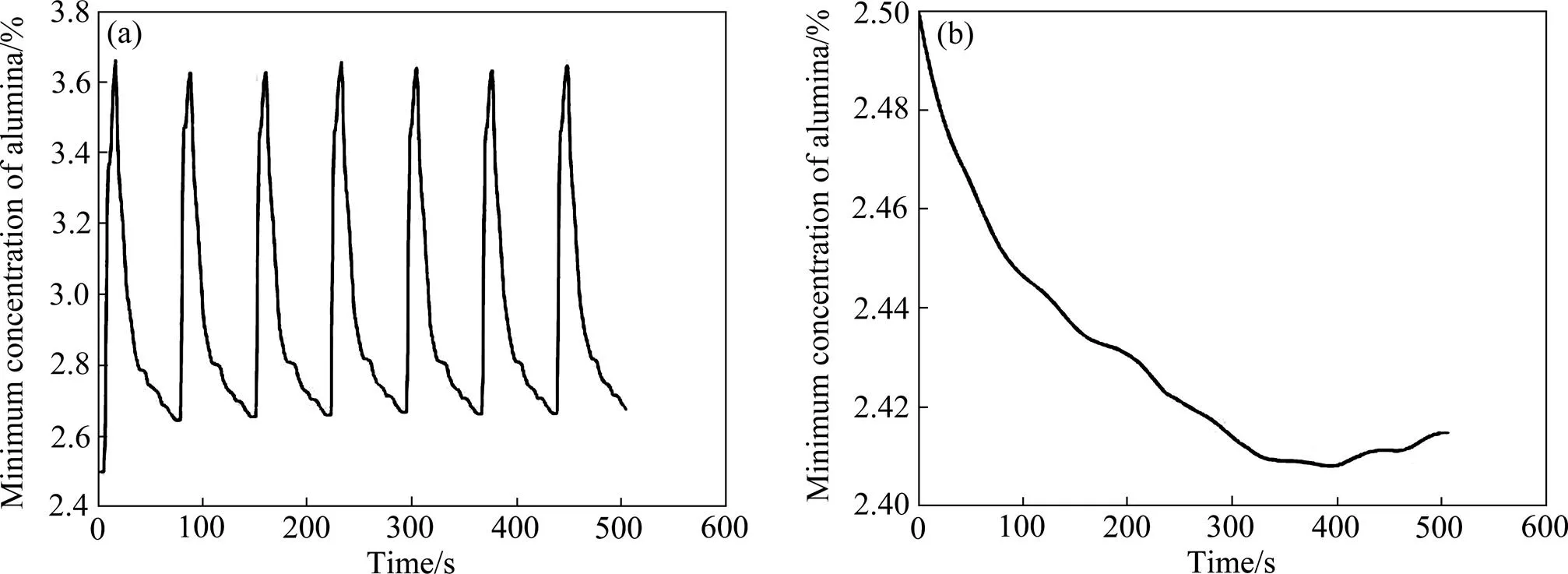
图4 XY面氧化铝浓度最大、最小浓度随时间周期性变化图

面(距离电解质上表面0.175 m)在极距中间，氧化铝颗粒到达面时温度已经升高较多，为了更全面地分析电解质上层区域温度变化趋势，本文作者进一步给出了1面(距离电解质表面0.08 m)上的最小温度及特征点(下料点附近)的温度随下料周期的变化曲线，分别如图7(a)和(b)所示。从图7(a)可以看出，在1面内，温度最多降低19 ℃左右；从图7(b)可以发现，点在下料期间温度迅速降低16 ℃左右，然后快速升温10 s左右，最后温度缓慢升至950 ℃保持不变。电解槽的过热度一般在10 ℃左右，在下料期间1面最小温度会降低超过10 ℃，这只是在电解质上表面附近很小的一部分区域，且很快会被加热到正常温度；极距层电解质温度场是电解槽正常运行的主要因素，在极距层温度最多降低5 ℃左右，属于正常范围内，不会影响电解槽的正常运行。

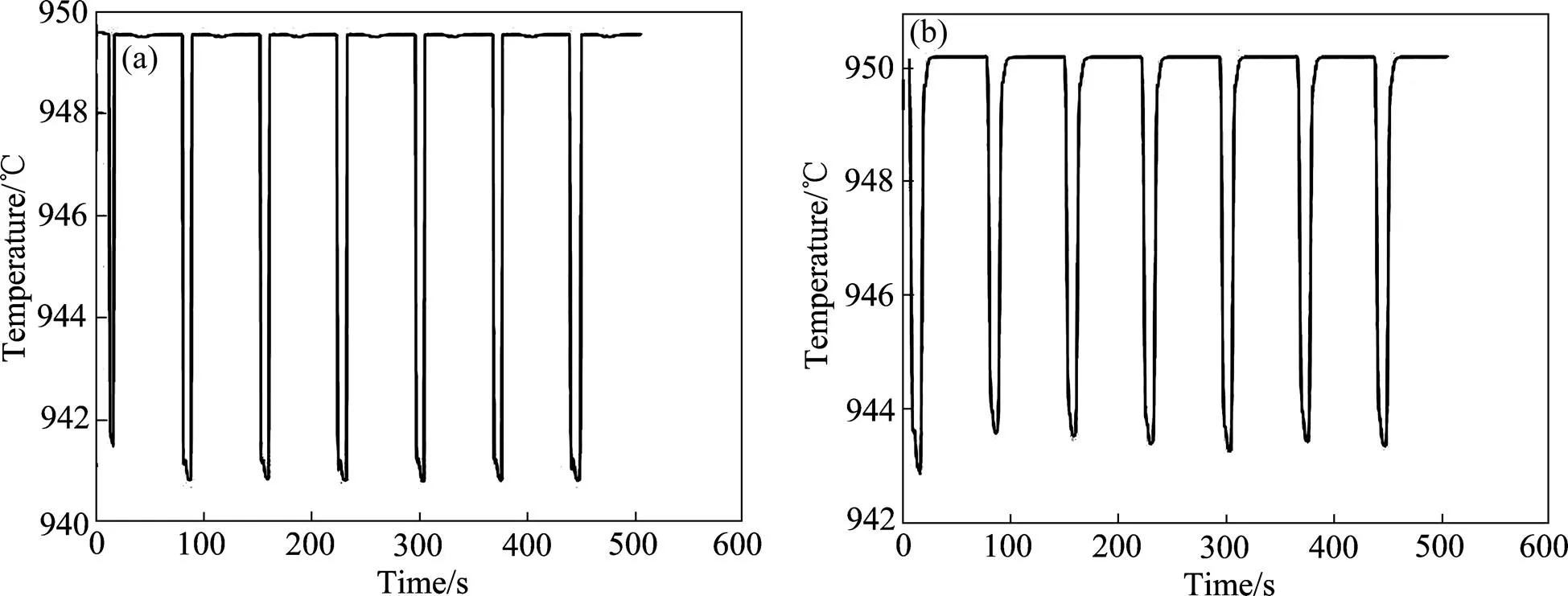
图7 电解质XY最小面温度和特征点P的温度随时间变化曲线

为了分析铝电解槽的热平衡，本文作者采用生热量(h)减去散热量(d)，即作为电解质的热平衡衡量指标。图8所示为电解质热平衡指标随时间的变化曲线。由图8可以看出，正常情况下电解质保持很好的热平衡，但下料过程会破坏原有的热平衡，部分产热量用来加热常温氧化铝，最高可达到300 kW(见图8(a))。随着氧化铝温度达到电解温度，电解质在下料后20 s左右达到新的热平衡(见图8(b))。

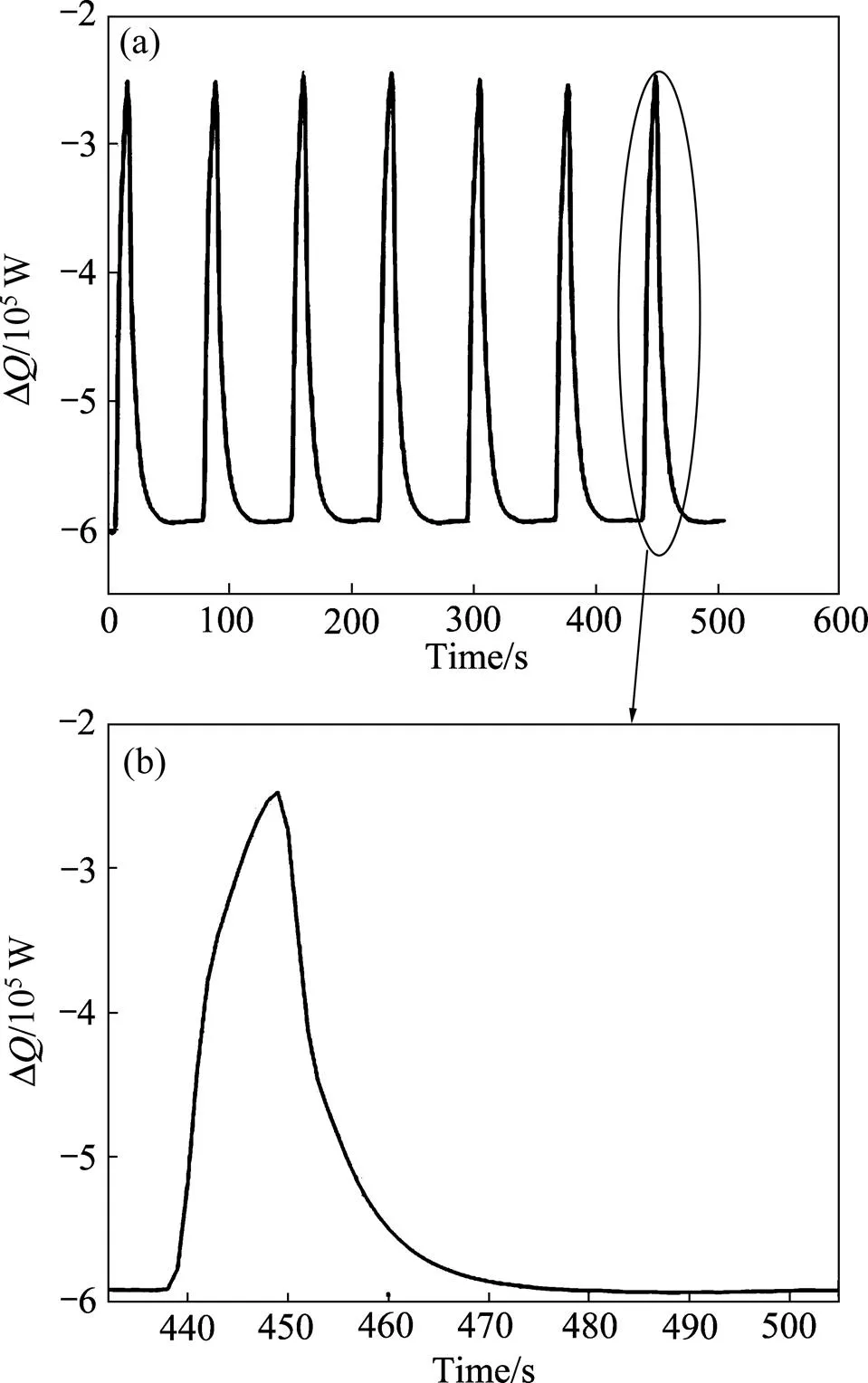
图8 电解质热平衡随时间变化曲线

基于以上分析可以发现，下料期间极距层的电解质温度最多降低5 ℃左右，电解质上表面小部分区域会降低到十几度，但很快会被加热，下料结束十几秒内，常温氧化铝会被加热到正常的电解温度。温度降低的电解质部分与氧化铝的浓度分布相关，且在氧化铝扩散过程总会被加热，因此，距离下料点较远的区域电解质温度几乎不受影响。下料会破坏电解质的热平衡，部分产热量会用来加热常温氧化铝颗粒，不过在下料结束20 s左右会形成新的热平衡。

4 结论

1) 本研究模型很好地模拟全槽氧化铝浓度分布。电解质流动带动氧化铝向全槽输运，同时氧化铝由高浓度区域向低浓度区域扩散，并且氧化铝浓度分布在时间和空间上呈现周期性稳定变化。

2) 在下料过程中，下料点下方的电解质温度，在电解质上表面附近降低十几度；下降过程中逐渐加热，在极距层只有5 ℃左右的下降变化。下料结束后，温度降低的电解质先快速升温10 s，然后缓慢上升，20 s左右电解温度达到950 ℃。

3) 下料期间热平衡会被破坏，部分热量用来加热氧化铝颗粒，最多每秒可达到300 kW。随后20 s左右，电解质温度会被加热到电解温度，且形成新的热平衡。

REFERENCES

[1] 杨 帅, 张红亮, 邹 忠, 赖延清, 李 劼. 铝电解槽内电解质与内衬界面换热系数的数值仿真研究[J]. 中国有色金属学报, 2015, 25(2): 515−522.
YANG Shuai, ZHANG Hong-liang, ZOU Zhong, LAI Yan-qing, LI Jie. Calculation of heat transfer coefficient between aluminum reduction cell surface and surroundings[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 515−522.

[2] 龙凤翔. 铝电解槽热平衡控制技术的开发[J]. 轻金属, 2002(10): 44−45.
LONG Feng-xiang. Development of heat balance control technique of aluminum reduction pot[J]. Light Metals, 2002(10): 44−45.

[3] TABSH I, DUPUIS M, GOMES A. Process simulation of aluminum reduction cells[R]. Warrendale, PA: Minerals, Metals and Materials Society, 1996.

[4] DUPUIS M, BOJAREVICS V, FREILBERGS J. Demonstration thermo-electric and MHD mathematical models of a 500 kA aluminum electrolysis cell: Part 2[C]// Light Metals-Warrendale- Proceedings. Warrendale: TMS, 2004: 453−460.

[5] DUPUIS M, BOJAREVICS V. Retrofit of a 500 kA cell design into a 600 kA cell design[J]. International Aluminum Journal, 2011, 87(1/2): 52−55.

[6] 崔喜风, 邹 忠, 张红亮, 李 劼, 徐宇杰. 预焙铝电解槽三维槽帮形状的模拟计算[J]. 中南大学学报(自然科学版), 2012, 43(3): 815−820.
CUI Xi-feng, ZOU Zhong, ZHANG Hong-liang, LI Jie, XU Yu-jie. Simulation calculation of 3D freeze profile in prebaked aluminum reduction cells[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 815−820.

[7] CUI Xi-feng, ZHANG Hong-liang, ZOU Zhong, LI Jie, LIU Yan-qing, XU Yu-jie, LIU Xiao-jun. 3D Freeze shape study of the aluminum electrolysis cells using finite element method[C]// JOHNSON J A. Light Metals 2010. Warrendale, PA: TMS, 2010: 447−452.

[8] THOMAS H. Numerical simulation and optimization of the alumina distribution in an aluminium electrolysis pot[D]. Lausanne: École Polytechnique Fédérale de Lausanne, 2011.

[9] 詹水清, 李 茂, 周孑民, 周益文, 杨建红. 铝电解槽熔体内氧化铝浓度分布的数值模拟[J]. 中国有色金属学报, 2014, 24(10): 2658−2667.
ZHAN Shui-qing, LI Mao, ZHOU Jie-min, ZHOU Yi-wen, YANG Jian-hong. Numerical simulation of anodic bubble distribution in aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2658−2667.

[10] 张翮辉. 铝电解槽内熔体涡运动与氧化铝输运过程的数值模拟研究[D]. 长沙: 中南大学, 2012.
ZHANG He-hui. Numerical study of vortex flow of melts and transport process of alumina in aluminum reduction cells[D]. Changsha: Central South University, 2012.

[11] ZHANG Hong-liang, YANG Shuai, ZHANG He-hui, LI Jie, XU Yu-jie. Numerical simulation of alumina-mixing process with a multicomponent flow model coupled with electromagnetic forces in aluminum reduction cells[J]. JOM, 2014, 66(7): 1210−1217.

[12] 江 南, 邱泽晶, 张翮辉, 张红亮, 杨 帅, 李 劼, 刘庆生. 500 kA级铝电解槽内氧化铝浓度场的数值模拟[J]. 中国有色金属学报, 2015, 25(3): 799−805.
JIANG Nan, QIU Ze-jing, ZHANG He-hui, ZHANG Hong-liang, YANG Shuai, LI Jie, LIU Qing-sheng. Numerical simulation of alumina concentration field in 500 kA aluminum reduction cell[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(3): 799−805.

[13] 薛玉卿. 铝电解槽阳极气泡的生成机理和运动规律[D]. 长沙: 中南大学, 2006.
XUE Yu-qing. Theory studies on the growth mechanics and velocity of anodic bubbles[D]. Changsha: Central South University, 2006.

[14] 詹水清, 周孑民, 李茂, 董 英, 周益文, 杨建红. 铝电解槽熔体内阳极气泡分布特性的数值模拟[J]. 中南大学学报(自然科学版), 2014, 45(7): 2424−2431.
ZHAN Shui-qing, ZHOU Jie-min, LI Mao, DONG Ying, ZHOU Yi-wen, YANG Jian-hong. Numerical simulation of anodic bubble distribution in aluminum reduction cells[J]. Journal of Central South University (Science and Technology), 2014, 45(7): 2424−2431.

[15] 岑可法, 樊建人. 工程气固多相流动的理论及计算[M]. 杭州: 浙江大学出版社, 1990.
CEN Ke-fa, FAN Jian-ren. Theory and calculation of gas solid multiphase flow[M]. Hangzhou: Zhejiang University press, 1990.

[16] TAYLOR M P, ZHANG W D, WILLS V, SCHMID S. A dynamic model for the energy balance of an electrolysis cell[J]. Chemical Engineering Research and Design, 1996, 74(8): 913−933.

[17] KOLENDA Z S, NOWAKOWSKI J, OBĿAKOWSKI R. Measurements of thermophysical properties of liquid electrolyte by modified heat pulse technique[J]. International Journal of Heat and Mass Transfer, 1981, 24(5): 891−894.

[18] 李 劼, 张翮辉, 张红亮, 徐宇杰, 杨 帅, 赖延清. 大型铝电解槽电解质流场涡结构的数值模拟[J]. 中国有色金属学报, 2012, 22(7): 2082−2089.
LI Jie, ZHANG He-hui, ZHANG Hong-liang, XU Yu-jie, YANG Shuai, LAI Yan-qing. Numerical simulation on vortical structures of electrolyte flow field in large aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 2082−2089.

(编辑 李艳红)

Effect of feeding in aluminum reduction cell on electrolyte temperature

DING Pei-lin1, WANG Heng1, HUANG Jun2, WANG Zi-qian2, CAO Bin2

(1. Department of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China;2. Guiyang Aluminum-Magnesium Design and Research Institute Co., Ltd., Guiyang 550081, China)

Keeping good heat balance in the aluminum reduction cell can decrease the energy consumption in the process of aluminum electrolysis, but the feeding can destroy the heat balance. The transient model of alumina concentration and thermal field in cell was established. Based on the accurate simulation of the alumina concentration distribution, the temperature and heat balance were studied. The results show that the local electrolyte temperature decrease about 5 ℃ in the electrolyte space layer and the dozen degrees around the bath surface, and gradually restored to the original temperature after 20 s. The feeding can break the heat balance of the cell, and heat at 300 kW is used to heat the alumina particles. After 20 s, the cell reaches a new heat balance state.

aluminum reduction cell; alumina concentration distribution; concentration; thermal field; heat balance

Project(2013DFB70220) supported by the National Science and Technology Cooperation of China

2015-08-11; Accepted date: 2015-12-02

DING Pei-lin; Tel: +86-13387545829; E-mail: dingpeilin@hust.edu.cn

1004-0609(2016)02-0430-09

TF821

A

国家国际科技合作专项项目(2013DFB70220)

2015-04-08；

2015-12-08

丁培林；电话：13387545829；E-mail：dingpeilin@hust.edu.cn