氧化铝颗粒的溶解控制机制及其临界特征
李 茂,白 晓,李 远,侯文渊,高玉婷
氧化铝颗粒的溶解控制机制及其临界特征
李 茂,白 晓,李 远,侯文渊,高玉婷
(中南大学 能源科学与工程学院,长沙 410083)
在铝电解工艺中,氧化铝在电解质中的溶解同时受传热与传质的控制。通过建立氧化铝颗粒溶解的传热控制模型、传质控制模型以及收缩核模型,基于OpenFOAM开源软件平台,采用自编程的方法开发氧化铝溶解求解模块,对氧化铝颗粒在两种控制机制下的溶解进行数值模拟。结果表明:在传质机制控制下,其颗粒的质量溶解速率及其速率的变化梯度均随粒径的减小而降低;在传热机制控制下,其颗粒质量溶解速率也随颗粒粒径的减小而减小,但速率梯度变化不大。为了区分氧化铝溶解过程中传热与传质两种控制机制中哪种机制占主导作用,提出临界直径的定义及其判定。研究得出氧化铝颗粒临界直径为560 μm,小于560 μm的氧化铝颗粒溶解受传质机制的控制,大于560 μm的氧化铝颗粒溶解受传热机制的控制。
铝电解;氧化铝溶解;传质控制机制;传热控制机制;临界直径
氧化铝是铝电解过程中最主要的原料之一,加入电解槽后溶于电解质中并在电解作用下在阴极附近生成铝液,在阳极炭块附近生成二氧化碳[1]。氧化铝在电解质中的溶解过程非常复杂,与周围的氧化铝浓度、电解质流场和温度有关,且氧化铝在电解质中溶解的好坏直接决定了电解工艺的稳定性[2]。如果氧化铝颗粒聚集、周围氧化铝浓度过高或因局部吸热过多导致电解质温度过低造成氧化铝结块,溶解不了的结块沉降就会在阴极炭块表面形成沉淀(软泥)和结壳,沉淀会侵蚀阴极,增大电阻,降低电流效率,增加阳极效应次数,增加耗能并造成热场不均,最终造成铝液层的不稳定,此外过多的沉淀还会增加过热度,破坏电解槽的热平衡[3−4]。
目前国内外学者对氧化铝溶解过程的反应机理以及影响氧化铝溶解的因素进行了大量实验与机理研究,也在此基础上提出了许多溶解模型。ROLSETH等[5]和WELCH等[6]根据实验数据拟合提出氧化铝溶解半经验模型,但由于受实验条件和槽型的影响较大,此模型实际应用的较少;HAVERKAMP等[7]和徐宁 等[8]运用化学反应动力学的方法建立了氧化铝溶解化学反应控制模型,相关参数及反应机理不完善,且模型较为复杂,计算难度较大;POI等[9]和VERHAEGHE等[10]认为氧化铝溶解的驱动力是氧化铝浓度差,以此提出氧化铝传质控制溶解模型;而LILLEBUEN等[11]和BEREZIN等[12]则认为电解质温度与初晶温度差,即过热度为驱动氧化铝溶解的主要因素,从而提出了氧化铝传热控制溶解模型。传热控制模型和传质控制模型能够比较准确地反映氧化铝溶解过程,因此被多数学者认可[13]。近年来一些学者认为氧化铝颗粒溶解受传质与传热两种机制的综合控制,其中TAYLOR 等[14]基于实验预测粒径大于400 μm的颗粒受传热机制的控制,小于400 μm的颗粒受传质机制的控制;而ZHAN等[15−16]提出TPPBM方法研究氧化铝颗粒群的溶解,并将500 μm的颗粒粒径作为两种控制机制作用的区分粒径,利用数值模拟的手段进行分析求解。然而以上特征粒径均为根据实验结果提出的猜想,或未进行实际验证和理论推导,或未考虑固相氧化铝颗粒的不同尺寸在电解质中对溶解的影响[17−18],因此有待进一步深入研究。
基于上述文献研究成果,本文作者从传质与传热的角度出发,分别建立通用的氧化铝传质控制和传热控制溶解模型,运用OpenFOAM开源软件开发氧化铝溶解求解模块,同时考虑氧化铝浓度与电解质温度变化对颗粒溶解的影响,重点研究区分传质与传热两种机制哪种机制占主导控制作用的临界直径,为氧化铝溶解控制机制的微观特征研究提供实际理论依据。
1 氧化铝颗粒溶解模型
目前国内外学者虽提出了多种氧化铝溶解模型,但模型相对复杂且不适宜进行仿真计算,相关参数获取较困难,因此本研究不采用现已提出的溶解模型,而是从传质与传热的角度出发,经过理论分析与数学推导计算,建立氧化铝传质、传热溶解模型,以此解决模型的通用性问题。
1.1 传质控制模型
假设氧化铝颗粒为球形颗粒,则氧化铝颗粒在电解质中的流动与传质过程满足如下无量纲方程[19−21]:
由式(1)可求得传质系数:
通过求得的传质系数,并结合传质控制方程的原理:氧化铝溶解的驱动力是电解质中的氧化铝浓度差,即氧化铝颗粒表面浓度(饱和浓度)与电解质中氧化铝浓度差,得到氧化铝颗粒在传质控制下的质量变化速率如式(3)所示[22]:
式中:sat和分别为电解质中氧化铝的饱和体积浓度和表面体积浓度,%;L为电解质密度,kg/m3。
由式(1)~(3)可以求得在传质机制下氧化铝颗粒的收缩核模型表达式如式(4)所示:
1.2 传热控制模型
氧化铝颗粒在电解质中的流动与传热过程满足如下无量纲方程[19−20]:
由式(5)可求得对流换热系数:
根据传热控制机理:电解质过热度是氧化铝溶解驱动力,得到氧化铝颗粒在传热控制下的质量变化速率如式(7)所示[7]:
式中:Lliq和Al分别为电解质温度、电解质液相线温度和氧化铝颗粒的温度,K;c.Al为氧化铝颗粒比热容,J/(kg·K);Δdiss为氧化铝颗粒溶解热,J/kg。
由式(5)~(7)联立求得在传热机制下氧化铝颗粒收缩核模型表达式如下:
2 模型求解
2.1 物理模型
着重研究氧化铝颗粒在传质、传热机制控制下的溶解,同时计算氧化铝溶解造成的电解质温度、电解质中氧化铝浓度以及颗粒粒径的变化规律,在保证求解精度以及反映客观规律的前提下,将实际电解槽结构以及流场区域进行如下简化假设:
1) 氧化铝颗粒为均匀的球形颗粒;
2) 电解质流动区域为10 m×1 m×0.1 m(长× 宽×高),下料区为1 cm正方体区域,俯视图如图1所示;

图1 计算区域示意图
3) 实际电解槽中电解质平均流速为0.1 m/s[23],假设整个电解质流场初始速度为0.1 m/s,从左侧流入,右侧出口流出;
4) 忽略颗粒对电解质流动的影响;
5) 假定壁面是绝热的,电解质与外部环境没有能量交换,仅与氧化铝溶解吸热有关。
由于本模型为规则的几何体,为提高计算精度,网格间距设为1 cm,共生成1×106个六面体网格。
2.2 数学模型
2.2.1 曳力模型
在多数颗粒−流体两相流动过程中,曳力是控制颗粒流动的主要作用力,对于氧化铝颗粒,选用曳力模型如下式所示[19]:
利用拉格朗日的方法对氧化铝颗粒运动进行追踪,通过对单个氧化铝颗粒进行受力分析,运用牛顿第二定律:
将式(9)~(12)联立求解,可获取氧化铝颗粒每一时刻的位置以及速度,即氧化铝颗粒的运动轨迹。
2.2.2 输运模型
氧化铝颗粒一旦溶解,溶解区域电解质中氧化铝浓度会升高,此后氧化铝颗粒在浓度梯度以及对流的共同作用下会发生扩散,建立氧化铝浓度输运方程如式(13)所示:
氧化铝在溶解过程中吸收热量,包括溶解热以及将冷的氧化铝颗粒加热到电解质温度所需的热量,因此在氧化铝溶解过程中电解质温度会下降,建立如下能量方程:
2.3 边界条件
1) 入口边界条件
入口边界设置为速度入口,现场测试以及数值模拟结果表明电解质平均流速为0.1 m/s左右,入口速度设置为0.1 m/s[23],同时设定初始电解质温度为1233 K,氧化铝的饱和浓度为10%,初始浓度为3%。
2) 出口边界条件
出口采用压力出口边界,设置出口压力为0。
3) 壁面边界条件
电解质下部与铝液接触,上部与空气接触,因简化模型未考虑铝液和气泡对电解质的影响,因此将上下壁面设置为对称面[23],即垂直于上下壁面的速度分量为0,且沿上下壁面法线方向所有变量的梯度为0,即:
其余壁面设置为无滑移固定壁面,即壁面上各速度分量为0。
2.4 计算工况
实际铝电解工业中所用的氧化铝颗粒粒径一般在40~200 μm之间,这些氧化铝颗粒在加入到电解质后,一部分颗粒快速分散而迅速溶解,另一部分则会聚集到一起形成结块,这部分结块粒径在1~15 mm之间。考虑到计算成本,本文作者选取1 mm结块氧化铝颗粒作为研究对象,对其溶解过程进行模拟计算以分析氧化铝颗粒质量溶解速率随粒径的变化关系。电解质中初始氧化铝浓度取为3%,在实际电解过程中浓度一般控制在1.5%~3.5%[24],为了控制氧化铝浓度波动的范围,在图1的下料区内加入10.34 g氧化铝,相当于增加下料区浓度1%。
结块氧化铝颗粒密度为2975 kg/m3[22],经计算,10.34 g氧化铝中有10000个1 mm的单个氧化铝颗粒。数值计算10000个颗粒耗时较长,在不影响计算准确度的情况下进行简化,只计算一个颗粒在电解质中的运动,但在计算输运方程时,所计算的质量源项和热源项扩大10000倍来代表10000个颗粒溶解造成的质量浓度和温度的变化。这样既减少了计算费用,也不影响计算结果的准确性。
3 结果与讨论
3.1 传质机制下氧化铝溶解分析
3.1.1 传质机制下质量溶解速率分析
氧化铝颗粒质量溶解速率受颗粒粒径的大小影响较大,图2所示为传质机制控制下的氧化铝质量溶解速率随粒径的变化关系曲线。由图2可知,氧化铝颗粒在溶解过程中,溶解速率从900 μm时的2.37×10−8kg/s下降到200 μm时的0.07×10−8kg/s,质量溶解速率及其变化梯度均随粒径的减小而降低。质量溶解速率与氧化铝颗粒反应表面积密切相关,初始时刻,氧化铝颗粒粒径较大,由式(3)可知此时反应表面积较大,故氧化铝溶解速率较大,即单位时间内能溶解的氧化铝质量越大,随着氧化铝逐渐溶解,颗粒粒径减小导致反应表面积减小,质量溶解速率逐渐降低。
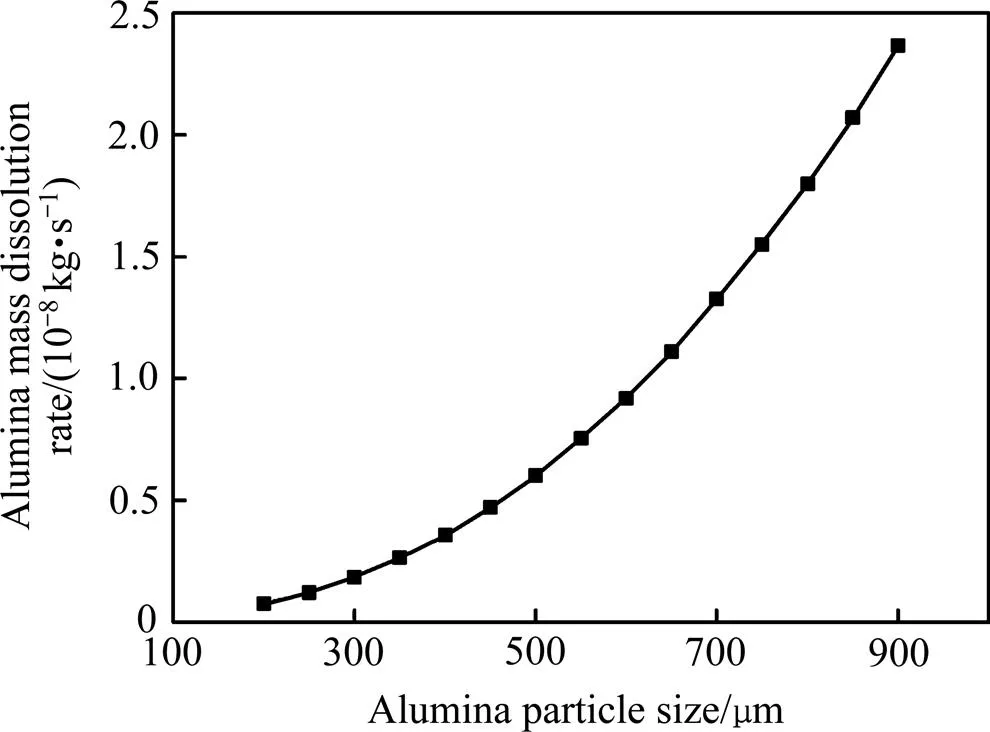
图2 传质机制控制下的氧化铝质量溶解速率随粒径的变化曲线

图3 传质机制控制下的氧化铝溶解质量及粒径随时间变化曲线
3.1.2 传质机制下氧化铝浓度分布
氧化铝颗粒的溶解致使电解质中氧化铝浓度升高,而传质机制是利用浓度差来控制氧化铝的溶解速率。传质机制控制下不同时刻计算区域内氧化铝浓度分布云图如图4所示。1~3 s内,由于结块较大的氧化铝颗粒密度比电解质密度大,这一阶段氧化铝颗粒处于下沉状态,高氧化铝浓度区随颗粒不断下移,同时已溶解的氧化铝在电解质流动以及浓度梯度的共同作用下扩散,氧化铝溶解所形成的高浓度区与颗粒处于同一竖直区域内,说明氧化铝颗粒的速度在曳力作用下基本接近电解质流速;3 s后,氧化铝颗粒到达底部,因与下壁面碰撞造成能量损失,颗粒的运动速度小于电解质流速,电解质带动已溶解的氧化铝向右侧快速流动扩散,致使颗粒右侧氧化铝浓度高于3%。此外,计算单元最大氧化铝浓度在前3 s逐渐增加,最高达到3.63%;随着氧化铝颗粒沉入底部,氧化铝浓度逐渐减小,原因有二:一是前3 s内氧化铝颗粒运动速度与电解质流速基本相同,氧化铝颗粒一直处于高浓度区,新溶解的氧化铝可增加氧化铝浓度,但在3 s以后由于与下壁面碰撞,氧化铝颗粒运动速度减小,氧化铝颗粒一直处于从低浓度区流过来的电解质区域中,导致氧化铝浓度不能累积增加;二是随着氧化铝颗粒的逐渐溶解,颗粒粒径越来越小,从图2可以看出颗粒质量溶解速率随粒径的减小而降低,故溶解的氧化铝质量就越来越少,因此浓度逐渐减小。在实际铝电解过程中,为促进氧化铝溶解,可增大电解质的搅动,使电解质中氧化铝浓度更加均匀,避免因局部浓度过高引起溶解速率下降。

图4 传质机制控制下不同时刻氧化铝浓度场分布云图
3.2 传热机制下氧化铝溶解分析
3.2.1 传热机制下质量溶解速率分析
氧化铝溶解是一个吸热过程,电解质温度会由于氧化铝的溶解吸热而下降。式(8)表明,温度的变化会影响氧化铝的溶解速率,而在已公开文献中,学者对氧化铝溶解的模拟均非动态模拟,没有考虑氧化铝溶解的温度响应过程。因而本研究利用传热控制模型求解氧化铝溶解过程时,需要同时考虑氧化铝溶解吸热对电解质温度的影响。
1 mm氧化铝颗粒在传热机制控制下的质量溶解速率与粒径的关系曲线如图5所示。其溶解速率变化总体趋势与传质机制控制下的类似,均随氧化铝颗粒粒径的减小而缓慢减小。在传热机制控制下氧化铝颗粒的溶解速率从900 μm时的1.05×10−8kg/s下降到200 μm时的0.43×10−8kg/s,比传质机制下结块氧化铝颗粒的溶解速率变化范围要小,且质量溶解速率梯度变化不大。此外,不论氧化铝颗粒受传质机制还是传热机制控制,颗粒粒径决定了质量溶解速率的大小,粒径越大,其质量溶解速率就越大。

图5 传热机制控制下的氧化铝质量溶解速率随粒径的变化曲线
图6所示为传热机制控制下的氧化铝溶解累积质量分数及粒径随时间的变化曲线。由图6可知,1 mm氧化铝颗粒完全溶解需要110 s,而在其完全溶解时间的一半左右,即在55 s时氧化铝颗粒溶解的质量分数为55%,与传质控制下的氧化铝颗粒在30 s时溶解60%形成鲜明对比,说明传热机制控制下的溶解速率较传质机制下的小。图6中氧化铝颗粒粒径随时间的下降曲线表明,虽然颗粒的质量溶解速率变化比较平缓,但颗粒粒径变化梯度较大,颗粒尺寸溶解速率随粒径的减小而逐渐增大,粒径从400 μm到完全溶解仅用10 s左右的时间,比传质控制下的溶解时间要短得多。

图6 传热机制控制下的氧化铝溶解累积质量及粒径随时间变化曲线
3.2.2 传热机制下氧化铝浓度分布
传热机制控制下的氧化铝溶解规律和传质机制的溶解情况类似,如图7所示。在前3 s内氧化铝颗粒处于下落状态,电解质中氧化铝高浓度区域逐渐下降;3 s以后由于电解质流速大于颗粒运动速度,已溶入电解质的氧化铝relationcentageer成分在对流扩散作用下快速向右侧移动,因此颗粒右侧区域氧化铝浓度高于3%,且沿轴方向浓度逐渐减小。前3 s内计算单元最大氧化铝浓度为3.3%,比传质机制下达到的最大氧化铝浓度(3.63%)小,图2和图5对比可知,在单一机制控制作用下,大粒径的氧化铝颗粒在传质机制控制下的溶解速率要高于传热机制下溶解速率,因此两种机制何时起主导控制作用值得深入探究。

图7 传热机制控制下不同时刻氧化铝浓度场分布云图
3.2.3 传热机制下电解质温度分布
氧化铝溶解吸热会引起电解质温度下降,因此溶解过程中氧化铝颗粒周边电解质温度会下降。图8所示为传热机制控制下不同时刻计算区域电解质温度分布云图。氧化铝颗粒所在单元温度较低,在1 s时该单元电解质温度下降较明显;3 s时颗粒下沉到底部,这段时间内氧化铝继续溶解吸热,吸热量积累使得电解质温度进一步下降,但是下降量不大。当氧化铝颗粒落在底部时,由于电解质流速大于氧化铝颗粒运动速度,温度较低的电解质快速向右侧移动,同时与周围温度高的电解质进行对流换热,右侧电解质温度逐渐升高;在氧化铝颗粒不断溶解过程中,颗粒粒径逐渐减小,质量溶解速率也随之减小,可以看出3 s以后的电解质低温区处于氧化铝颗粒周边,且计算单元最低温度随着氧化铝颗粒的溶解不断升高,110 s时氧化铝已经基本溶解,颗粒周边温度仅下降4 ℃左右。图8中氧化铝周边的温度较其他地方温度低,由式(8)可知,电解质过热度降低会使得氧化铝溶解速率下降,因此在实际生产中为了提高氧化铝溶解速率,要促进因氧化铝溶解而形成的颗粒周边低温电解质的扩散。

图8 传热机制控制下不同时刻电解质温度分布云图
4 临界直径
根据上述传质和传热控制下氧化铝的溶解结果可以看出,在不同机制控制下氧化铝的溶解情况是不同的,那么氧化铝颗粒溶解到底受传质机制还是传热机制的控制,就需要根据哪种机制起主导控制作用来判断。
4.1 临界直径的定义
在铝电解槽中,氧化铝颗粒在电解质中的溶解过程受传质机制与传热机制双重控制作用,区分两种溶解控制机制中哪种机制占主导作用的粒径为临界直径。TAYLOR等[14]和ZHAN等[15]分别根据实验和计算提出了相应的400 μm和500 μm,但缺乏明确的基础分析和理论支撑。为深入研究铝电解槽中氧化铝颗粒的溶解控制机理,数值模拟提供了一个实际可行的理论分析手段。
4.2 临界直径的判定
通过对1 mm氧化铝颗粒分别进行传质控制、传热控制的溶解模拟,得到了氧化铝在不同粒径下的质量溶解速率如图9所示。无论是传质机制还是传热机制控制,溶解速率均随粒径的增加而增大。在560 μm左右,两种机制下的氧化铝颗粒质量溶解速率基本相同,氧化铝颗粒直径小于560 μm时,传热机制控制下的溶解速率大于传质机制控制下的溶解速率;颗粒直径大于560 μm时则相反,传热机制控制下的氧化铝质量溶解速率小于传质机制控制下的氧化铝质量溶解速率。

图9 氧化铝质量溶解速率与粒径的关系曲线
氧化铝颗粒的溶解是一个复杂的物理化学反应过程,可以描述为氧化铝与氟化铝的反应,反应方程式如式(16)和(17)所示[1]:
氧化铝浓度较低时:
氧化铝浓度较高时:
化学反应速率受内扩散与外扩散的控制,内扩散控制是指在氧化铝颗粒表面化学反应速率比氟化铝向氧化铝表面扩散速率大,溶解速率取决于氟化铝扩散速率;而外扩散控制是指氧化铝颗粒表面化学反应速率比氟化铝向氧化铝表面扩散速率小,溶解速率取决于化学反应速率[26]。
溶解反应属于吸热反应,化学反应速率与温度有关,电解质温度越高,过热度越大,根据传热控制理论可知,氧化铝溶解速率越大。而由Arrhenius公式也可得知,氧化铝溶解化学反应速率随电解质温度升高而增大,因此,传热机制类似于从氧化铝化学反应速率的角度进行控制。
Fick定律表明,氟化物向氧化铝表面扩散速率与氟化铝浓度梯度有关。当氧化铝溶解后氧化铝浓度升高,根据传质控制理论可知氧化铝饱和浓度与当地浓度差减小,溶解速率减慢,而氧化铝溶解反应使得当地氟化铝浓度降低,导致氟化铝浓度与颗粒表面氟化铝浓度差减小,扩散速率减慢,因此传质机制是从扩散速率的角度进行控制。
在氧化铝颗粒粒径小于560 μm时,传质控制机制下的质量溶解速率低于传热控制机制下的质量溶解速率,即扩散速率小于化学反应速率,属于内扩散控制。所以在颗粒粒径小于560 μm阶段,传质控制机制下的质量溶解速率成为氧化铝溶解速度的律速步骤,氧化铝受传质机制的控制;同理可知,在颗粒粒径大于560 μm的阶段,氧化铝受传热机制的控制。
5 结论
1) 分别从传热与传质的角度出发,建立氧化铝颗粒溶解的传热控制模型、传质控制模型以及收缩核模型,基于OpenFOAM开源软件平台,通过自编程的方法建立氧化铝溶解求解模块,计算研究氧化铝颗粒在两种机制控制下的溶解特征。
2) 氧化铝颗粒在传质机制和传热机制控制下的溶解,其颗粒质量溶解速率均随颗粒粒径的减小而减小,但传质机制下质量溶解速率的变化梯度随粒径的减小而降低,而传热机制下质量溶解速率梯度变化不大。
3) 提出传质与传热两种溶解机制综合作用下临界直径的定义及其判定,区分两种机制中哪种机制占主导控制作用的临界直径为560 μm。小于560 μm的氧化铝颗粒溶解受传质机制的控制,大于560 μm的氧化铝颗粒溶解受传热机制的控制。
REFERENCES
[1] 冯乃祥. 铝电解[M]. 北京: 化学工业出版社, 2006.
FENG Nai-xiang. Aluminum electrolysis[M]. Beijing: Chemical Industry Press, 2006.
[2] YANG You-jian, Gao Bing-liang, WANG Zhao-wen, SHI Zhong-ning, HU Xian-wei. Effect of physiochemical properties and bath chemistry on alumina dissolution rate in cryolite electrolyte[J]. JOM, 2015, 67(5): 973−983.
[3] 徐君莉, 石忠宁, 高炳亮, 邱竹贤. 氧化铝在熔融冰晶石中的溶解[J]. 东北大学学报: 自然科学版, 2003, 24(9): 832−834.
XU Jun-li, SHI Zhong-ning, GAO Bing-liang, QIU Zhu-xian. Dissolution of alumina in molten cryolite[J]. Journal of Northeastern University: Natural Science, 2003, 24(9): 832−834.
[4] 刘世英, 石忠宁, 邱竹贤, 任必军, 曹全红. 铝电解槽中沉淀的形成及分析[J]. 轻金属. 2006(7): 34−36.
LIU Shi-ying, SHI Zhong-ning, QIU Zhu-xian, REN Bi-jun, CAO Quan-hong. Sludge formation and analysis in aluminium reduction cells[J]. Light Metals, 2006(7): 34−36.
[5] ROLSETH S, HOVLAND R, KOBBELTVEDT O. Alumina agglomeration and dissolution in cryolitic melts[C]// MANNWEILER U. Light Metals1994. San Francisco, CA: TMS (The Minerals, Metals &Materials Society), 1994: 351−357.
[6] WELCH B J, KUSCHEL G I. Crust and alumina powder dissolution in aluminum smelting electrolytes[J]. JOM, 2007, 59(5): 50−54.
[7] HAVERKAMP R G, WELCH B J. Modelling the dissolution of alumina powder in cryolite[J]. Chemical Engineering and Processing: Process Intensification, 1998, 37(2): 177−187.
[8] 徐 宁, 杨振海, 邱竹贤, 程 涛. 氧化铝在冰晶石熔体中溶解的动力学模型[J]. 东北大学学报, 1999(3): 93−96.
XU Ning, YANG Zheng-hai, QIU Zhu-xian, CHENG Tao. Kinetic model of dissolution of alumina in molten cryolite[J]. Journal of Northeastern University, 1993(3): 93−96.
[9] POI N W, HAVERKAMP R G, KUBLER S. Thermal effects associated with alumina feeding in aluminium reduction cells[C]// MANNWEILER U. Light Metals1994. San Francisco, CA: TMS (The Minerals, Metals &Materials Society), 1994: 219−225.
[10] VERHAEGHE F, BLANPAIN B, WOLLANTS P. Dissolution of a solid sphere in a multicomponent liquid in a cubic enclosure[J]. Modelling and Simulation in Materials Science and Engineering. 2008, 16(4): 45007.
[11] LILLEBUEN B O R, BUGGE M, HOIE H. Alumina dissolution and current efficiency in Hall-Heroult cells[C]// BEARNE G. Light Metals2009. San Francisco, CA: TMS (The Minerals, Metals & Materials Society), 2009: 389−394.
[12] BEREZIN A I, ISAEVA L A, BELOLIPETSKY V M, POSKAZHOVA T V, SINELNIKOV V V. A model of Dissolution and Heating of Alumina Charged by Point-Feeding System in “Virtual Cell” program[C]// KVANDE H. Light Metals 2005. San Francisco, CA: TMS (The Minerals, Metals & Materials Society), 2005: 151−156.
[13] 张家奇. 基于数学模型的铝电解槽动态过程及其预报系统研究[D]. 长沙: 中南大学, 2011.
ZHANG Jia-qi. Principal electrolysis processes and corresponding prediction system for aluminum electrolysis cells based on mathematical models[D]. Changsha: Central South University, 2011.
[14] TAYLOR M P, WELCH B J, MCKIBBIN R. Effect of convective heat transfer and phase change on the stability of aluminium smelting cells[J]. AIChE Journal, 1986, 32(9): 1459−1465.
[15] ZHAN Shui-qing, LI Mao, ZHOU Jie-min, YANG Jian-hong, ZHOU Yi-wen. CFD simulation of dissolution process of alumina in an aluminum reduction cell with two-particle phase population balance model[J]. Applied Thermal Engineering. 2014, 73(1): 803−816.
[16] ZHAN Shui-qing, LI Mao, ZHOU Jie-min, YANG Jian-hong, ZHOU Yi-wen. Analysis and modeling of alumina dissolution based on heat and mass transfer[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(5): 1648−1656.
[17] 詹水清, 李 茂, 周孑民, 周益文, 杨建红. 铝电解槽熔体内氧化铝浓度分布的数值模拟[J]. 中国有色金属学报, 2014, 24(10): 2658−2667.
ZHAN Shui-qing, LI Mao, ZHOU Jie-min, ZHOU Yi-wen, YANG Jian-hong. Numerical simulation of alumina concentration distribution in melts of aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2658−2667.
[18] 江 南, 邱泽晶, 张翮辉, 张红亮, 杨 帅, 李 劼, 刘庆生. 500 kA级铝电槽内氧化铝浓度场的数值模拟[J]. 中国有色金属学报, 2015, 25(3): 799−805.
JIANG Nan, QIU Ze-jing, ZHANG He-hui, ZHANG Hong-liang, YANG Shuai, LI Jie, LIU Qing-sheng. Numerical simulation of alumina concentration field in 500 kA aluminum reduction cell[J]. The Chinese Journal of Nonferrous Metals. 2015, 25(3): 799−805.
[19] 胡道和, 徐德龙, 蔡玉良. 气固过程工程学及其在水泥工业中的应用[M]. 武汉: 武汉理工大学出版社, 2003: 146−148.
HU Dao-he, XU De-long, CAI Yu-liang. Gas-solid process engineering and its application in the cement industry[M]. Wuhan: Wuhan University of Technology Press, 2003: 146−148.
[20] WELTYJ R, WICKS C E, WILSON R E, RORRER G L. 动量、热量和质量传递原理[M]. 马紫峰, 吴卫生, 译. 北京: 化学工业出版社, 2005.
WELTY J R, WICKS C E, WILSON R E, RORRER G L. Fundanmentals of momentum, heat, and mass transfer[M]. MA Zi-feng, WU Wei-sheng, transl. Beijing: Chemical Industry Press, 2005.
[21] 侯文渊, 李 茂, 李 远, 白 晓. 氧化铝颗粒在传质机制控制下的溶解模拟[J]. 轻金属, 2015(5): 24−28.
Hou Wen-yuan, LI Mao, LI Yuan, BAI Xiao. Simulation of alumina particle dissolution under the control of mass transfer mechanism[J]. Light Metals. 2015(5): 24−28.
[22] THONSTAD J, SOLHEIM A, ROLSETH S, SKAR O. The dissolution of alumina in cryolite melts[C]// BOXALL L G. Light Metals 1988. Phoenix, AZ: The Metallurgical Society of AIME, 1988: 105−111.
[23] 夏小霞. 铝电解槽内电解质流场的数值模拟研究[D]. 长沙: 中南大学, 2005.
XIA Xiao-xia. study on numerical simulation of the flow field in aluminum reduction electrolyte cells[D]. Changsha: Central South University, 2005.
[24] 任晓宁. 铝电解过程氧化铝浓度自适应控制研究[D]. 北京: 北方工业大学, 2012.
REN Xiao-ning. Study on adaptive control model to control alumina concentration in aluminum electrolysis[D]. Beijing: North China University of Technology, 2012.
[25] KUSCHEL G I, WELCH B J. Further studies of alumina dissolution under conditions similar to cell operation[C]// ELWIN R. Light Metals 1991. New Orleans, Louisiana: TMS (The Minerals, Metals & Materials Society), 1991: 112−118.
[26] 李洪桂. 冶金原理[M]. 北京: 科学出版社, 2005: 307−309.
LI Hong-gui. Metallurgical principle[M]. Beijing: Science Press, 2005: 307−309.
(编辑 王 超)
Control mechanisms and critical characteristics in dissolution of alumina particles
LI Mao, BAI Xiao, LI Yuan, HOU Wen-yuan, GAO Yu-ting
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
In the aluminum electrolytic process, alumina was dissolved in the electrolyte under the control of both heat and mass transfer mechanism. Heat transfer control model, mass transfer control model and the shrinking core model of alumina dissolution were established, Based on the OpenFOAM open source software platform, alumina dissolution solution module was set up by the custom code. Numerical simulations of the dissolution of alumina particles under the two mechanisms were conducted. The results show that under the control of mass transfer mechanism, the mass dissolution rate and the varying gradient of the mass dissolution rate of alumina particles reduce with decreasing the particle size. Under the control of heat transfer mechanism, the mass dissolution rate decreases with decreasing the particle size, while the varying gradient of the mass dissolution rate shows little change. In order to distinguish the dominance of the heat transfer or mass transfer control mechanism, the definition and judgement of the critical diameter were put forward. Considering the dissolution process of alumina particle is governed by mass transfer as well as heat transfer mechanism together, the critical diameter is 560 μm. The dissolution of alumina particles with the size of less than 560 μm is governed by mass transfer mechanism, while the dissolution of alumina particles with the size of more than 560 μm is under the control of the heat transfer mechanism.
aluminum reduction; alumina dissolution; mass transfer mechanism; heat transfer mechanism; critical diameter
Project(2010AA065201) supported by the National High Research Development Program of China
2015-06-29; Accepted date: 2015-10-28
LI Mao; Tel: +86-13055169363; E-mail: limao89@163.com
1004-0609(2016)02-0455-10
TF821;TP391
A
国家高技术研究发展计划资助项目(2010AA065201)
2015-06-29;
2015-10-28
李 茂,副教授,博士;电话:13055169363;E-mail: limao89@163.com

