数据不平衡分类研究综述

李元菊

（四川大学计算机学院，成都　610065）

数据不平衡分类研究综述

李元菊

（四川大学计算机学院，成都610065）

数据不平衡；抽样；代价敏感；集成方法

0　引言

在许多有监督的方法中，不同类别的先验概率有显著的差异，这种问题被称为类别不平衡问题[1-2]。这种问题在很多领域都经常出现，例如电信领域、网络、金融领域、生态学、生物学、医学等。在数据挖掘中，类别不平衡问题被认为是重要的待解决问题[3]。一般来说，少数类称为正类，多数类被称为负类，正类往往是我们研究的重点，当它不能很好地分类时往往需要花费较大的代价。

不平衡数据集的一个关键问题是标准的分类学习算法经常偏置向多数类。因此，对于少数类的样例来说有很高的误分类比率，为了解决这个问题专家们提出了很多办法。有数据层面的方法，也有算法层面的方法。主要分为三种：数据抽样，算法层面，代价敏感学习。

1　分类中的不平衡问题

1.1不平衡数据冀问题

在分类中，不平衡数据分类经常出现。这种分类问题的主要特点是某一种类别的样本数目明显多于其他类别样本数量[4]。然而少数类往往是我们重点学习的东西，在大多数情况下，不平衡数据分类通常指二分类，但是多分类也会出现这种情况，因为多分类会有多个少数类所以这种情况研究更困难[5-6]。

绝大多数标准学习算法针对的是平衡训练集，用这种学习算法来训练不平衡数据集往往产生的是次优的分类模型，例如这个模型可能覆盖了大多数的多数类样本，然而少数类样本经常被误分类。因此，这种算法在不平衡数据集上往往不能得到最好的效果。主要归因于下面几种原因：

①算法的度量指标如精确率、召回率对多数类有优势。

②预测正类的分类规则是高度专业化的，同时他们的覆盖率很低。因此，我们通常抛弃这些规则，取而代之的是可以预测负例的一般规则。

③非常少的少数类簇可以被定义为噪声，因此它们可能被分类器错误丢弃。相反，因为少数类有很少的训练集，所以少量真正的噪声实例可以降低少数类的识别。

1.2评估指标

在评估分类器的性能和指导分类器建模方面，评估标准发挥了关键作用。在传统的分类方法中，准确率是常用的指标。然而在不平衡数据分类中，准确率不再是恰当的指标[7-8]。在两类问题中，正例数目很少但具有很高的识别重要性，另一类为负例。样本经过分类处理后可以分为四组如下表混合矩阵[25]（表1）。

表1　混合矩阵

从该表我们可以得到下列度量指标：

真阳性率：TPrate=TP/（TP+FN），真阴性率：TNrate=TN/（TN+FP）

假阳性率：FPrate=FP/（TN+FP），假阴性率：FNrate= FN/（TP+FN）

阳性预测值:PPvalue=TP/（TP+FP），假性预测值：NPvalue=TN/（TN+FN）

上述度量指标都不能很好的评估不平衡数据分类，针对不平衡数据分类我们用几个新的度量指标如下：

（1）F-measure

在信息检索领域，真阳性率被称为recall，阳性预测值被称为精确率分别定义如下：

F-measure[9]是Precision和Recall的调和平均值。两个数值的调和平均更加接近两个数当中较小的那个，因此如果要使得F-measure很高的话那么Recall 和Precision都必须很高。

当两个类别的性能都需要考虑时，TPrate和TNrate需要同时高，Kubat等人[10]提出了G-mean。

G-mean评估一个学习算法的综合性能。根据之前的研究，为了能够获得尽可能多的关于每个类别对最终性能的贡献大小信息，并且考虑到数据的不平衡率，很多研究者试图在不平衡领域提出新的度量指标。如论文[11-12]调整了G-mean，提出了Adjusted G-mean。

G-mean评估一个学习算法的综合性能。根据之前的研究，为了能够获得尽可能多的关于每个类别对最终性能的贡献大小信息，并且考虑到数据的不平衡率，很多研究者试图在不平衡领域提出新的度量指标。如论文[11-12]调整了G-mean，提出了Adjusted G-mean。

（3）ROC曲线以及AUC

ROC曲线指受试者工作特征曲线（receiver operating characteristic curve）,是反映敏感性和特异性连续变量的综合指标,用构图法揭示敏感性和特异性的相互关系。在分类中每个样本属于不同类别对应的有概率值，最终类别预测根据设置的不同概率阈值，类别也会变化。每一个阈值对应的有一组衡量指标（FPrate, TPrate）,将FPrate为x轴，TPrate为y轴，在坐标轴上绘制图形。即可得到ROC曲线，曲线下方形成的面积即为AUC[13-14,24]。AUC从总体上度量了分类器的性能，一般来说面积越大，算法性能越好。图1 是一个ROC曲线的例子。

图1　ROC曲线

2　不平衡数据分类解决策略

2.1重新臭样技术

在一些专业文献中，我们发现一些文章采用重新抽样技术来改变不平衡数据集的类分布来调整数据平衡度。重新抽样技术主要有两种类型。

（1）欠抽样方法

欠抽样方法通过减少多数类样本的数目来平衡数据集。最简单的方法就是随机抽取多数类样本。但是由于这种方法具有随机性，所以可能丢失一些重要的信息。因此人们提出了一些改进的方法。

对于欠抽样技术，绝大多数是基于数据清洗技术。一些有代表性的工作有ENN规则[15]，该方法首先找到一个样例的k个邻居，当该样例的类标与2/3个k个近邻类标不同时，删除该样例。OSS算法[16]和Tomek Links算法[17]都是基于ENN技术。

（2）过抽样方法

通过增加少数类样本的数目来平衡数据，也是目前最常用的方法。通过复制原始少数类样本或者创造新的少数类样本来增加少数类样本的数目，来达到数据平衡的目的。

最简单的处理技术就是非启发式的方法例如随机过采样，这种方法因为它复制已有的实例所以很大可能会导致过度拟合。为了解决这种问题，出现了一些新的复杂方法。其中SMOTE算法[18]是最有名的、应用最广泛的方法。SMOTE算法利用线性插值的思想来创建少数类样本。主要思想如下：该方法首先为每个稀有类样本随机选出几个邻近样本,并且在该样本与这些邻近的样本的连线上随机取点,生成无重复的新的稀有类样本。SMOTE算法示意图如下：

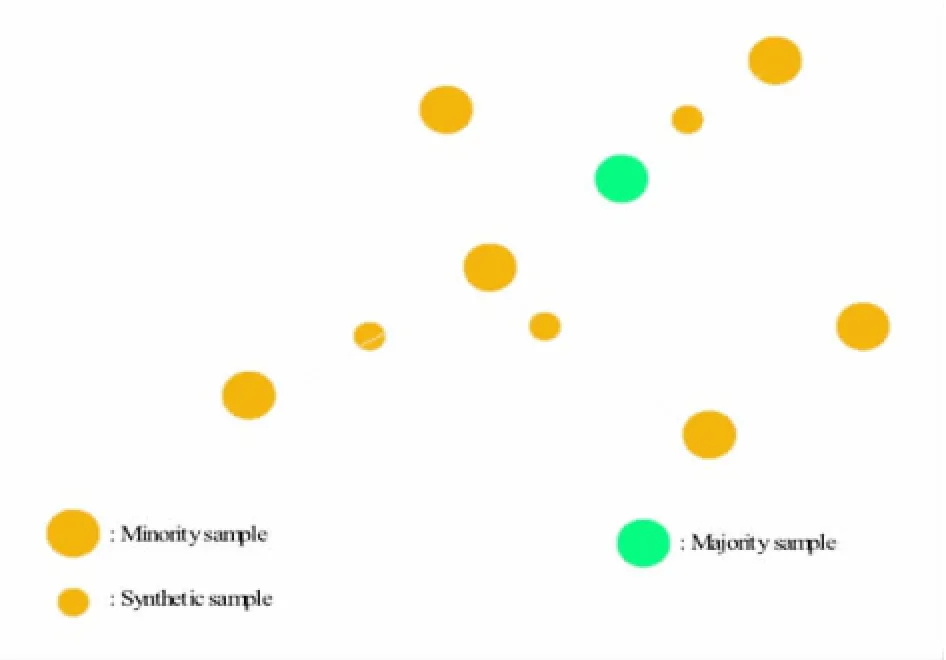
图2　SMOTE算法

2.2代价敏感算法

代价敏感学习赋予每个类别不同的误分类代价[19]，用C（i，j）表示将类别i误分为j的惩罚因子。针对二元分类我们定义一个代价矩阵如下表2所示。图中C（i，j）的值可以由专家给定，也可以通过方法学习得到[20-21]。具体地说当处理不平衡数据时我们感兴趣的是识别出正例而不是负例，所以误分类正例的代价要大于误分类负例代价。

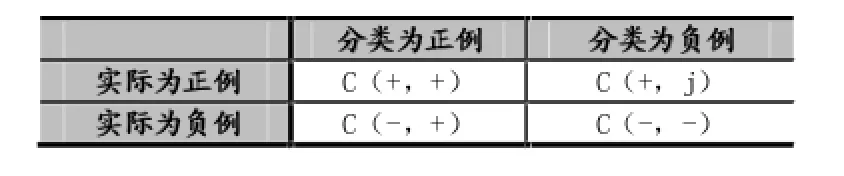
表2　代价矩阵

2.3集成算法

集成分类器将多个独立的分类器集成起来得到一个新的分类器，最终得到的模型优于独立的分类器。因此，基本的想法是用原始的数据集构造多个分类器，然后预测新样例时综合初始构造的多个基本分类器的最终结果。

近些年，集成分类器被用来解决数据不平衡分类。集成方法将集成算法与之前讨论的技术相结合，也就是数据层面和算法层面的方法。权重投票算法[14]提出了一个概率框架来进行分类器集成，这篇文章提出了四种结合方法，并给出了严格的最优条件即最小的误差。EasyEnsemble算法和BalanceCascade算法[22]利用了集成的方法，EasyEnsemble算法首先从多数类中欠抽样多个数据集，然后用AdaBoost算法分别训练抽样得到的多个数据集和少数类样本组成的多组训练集，EasyEnsemble是个无监督的算法。BalanceCascade算法是个有监督的算法，该方法仍然采用Adaboost算法，只不过每次从总的多数类数据集样本中去掉上次已被正确分类的样本。Cost-sensitive boosting[23]仍然采用boost算法，只不过给不同的样例分配不同的代价敏感因子。

3　结语

现实应用中存在着大量不平衡分类问题，迫切的需求激发了对不平衡分类的研究和分析。随着新的技术不断被提出，这一领域的工作也是越来越成熟。但是针对不平衡分类的研究并没有停止，近年来仍然有越来越多的研究者研究这一领域，同时不平衡数据分类仍然面临新的挑战和机遇。

[1]N.V.Chawla,N.Japkowicz,A.Kotcz,Editorial:Special Issue on Learning from Imbalanced Data Sets,SIGKDD Explorations，2004，6（1）：1-6.

[2]H.He,E.A.Garcia,Learning from Imbalanced Data,IEEE Transactions on Knowledge and Data Engineering，2009，21（9）：1263-1284.

[3]Q.Yang,X.Wu,10 Challenging Problems in Data Mining Research,International Journal of Information Technology and DecisionMaking，2006，5（4）：597-604.

[4]Y.Sun,A.K.C.Wong,M.S.Kamel,Classification of Imbalanced Data:a Review,International Journal of Pattern Recognition and Artificial Intelligence，2009，23（4）：687-719.

[5]A.Fernandez,V.Lopez,M.Galar,M.J.del Jesus,F.Herrera,Analysing the Classification of Imbalanced Data-Sets with Multiple Classes:Binarization Techniques and Ad-hoc Approaches,Knowledge-Based Systems 42，2013：97-110.

[6]M.Lin,K.Tang,X.Yao,Dynamic Sampling Approach to Training Neural Networks for Multiclass Imbalance Classification,IEEE Transactions on Neural Networks and Learning Systems，2013，24（4）：647-660.

[7]G.Weiss,Mining with Rarity:a Unifying Framework,SIGKDD Explorations Special Issue on Learning from Imbalanced Datasets, 2004，6（1）：7-19.

[8]M.V.Joshi,V.Kumar,R.C.Agarwal,Evaluating Boosting Algorithms to Classify Rare Classes:Comparison and Improvements,in: Proceedings of the First IEEE International Conference on Data Mining（ICDM’01），2001.

[9]D.Lewis,W.Gale,Training Text Classifiers by Uncertainty Sampling,in:Proceedings of the Seventeenth Annual International ACM SIGIR Conference on Research and Development in Information,New York,NY,August 1998：73-79

[10]M.Kubat,R.Holte,S.Matwin,Machine Learning for the Detection of Oil Spills in Satellite Radar Images,Mach.Learn.30，1998：195-215.

[11]R.Batuwita,V.Palade,AGm:a New Performance Measure for Class Imbalance Learning.Application to Bioinformatics Problems,in: Proceedings of the 8th International Conference on Machine Learning and Applications（ICMLA 2009）,2009：545-550.

[12]R.Batuwita,V.Palade,Adjusted Geometric-Mean:a Novel Performance Measure for Imbalanced Bioinformatics Datasets Learning, Journal of Bioinformatics and Computational Biology，2012，10（4）.

[13]Victoria LopezAlberto Fernandez.An Insight into Classification with Imbalanced Data:Empirical Results and Current Trends on Using Data Intrinsic Characteristics,Information Sciences，2013，250：113-141.

[14]叶志飞,文益民.不平衡分类问题研究综述.智能系统学报，2009，4（2）.

[15]D.L.Wilson,Asymptotic Properties of Nearest Neighbor Rules Using Edited Data,IEEE Transactions on Systems,Man and Cybernetics，1972，2（3）：408-421.

[16]M.Kubat,S.Matwin,Addressing the Curse of Imbalanced Training Sets:one-Sided Selection,in:Proceedings of the 14th International Conference on Machine Learning（ICML'97）,1997：179-186.

[17]I.Tomek,Two modifications of CNN,IEEE Transactions on Systems Man and Communications，1976，6：769-772.

[18]N.V.Chawla,K.W.Bowyer,L.O.Hall,W.P.Kegelmeyer,SMOTE:Synthetic Minority Over-Sampling Technique,Journal of Artificial Intelligent Research，2002，16.

[19]P.Domingos,Metacost:a General Method for Making Classifiers Cost-Sensitive,in:Proceedings of the 5th International Conference on Knowledge Discovery and Data Mining（KDD'99）,1999：155-164.

[20]Y.Sun,M.S.Kamel,A.K.C.Wong,Y.Wang,Cost-Sensitive Boosting for Classification of Imbalanced Data,Pattern Recognition 40 2007（12）：3358-3378.

[21]Y.Sun,A.K.C.Wong,M.S.Kamel,Classification of Imbalanced Data:a Review,International Journal of Pattern Recognition and Artificial Intelligence 23

[22]X.-Y.Liu,J.Wu,Z.-H.Zhou,Exploratory Undersampling for Class-Imbalance Learning,IEEE Transactions on System,Man and Cybernetics B，2009，39（2）：539-550.

[23]Y.Sun,M.S.Kamel,A.K.C.Wong,Y.Wang,Cost-Sensitive Boosting for Classification of Imbalanced Data,Pattern Recognition 40, 2007，12：3358-3378.

[24]倪黄晶，王蔚.多类不平衡数据上的分类器性能比较研究.计算机工程，2011，37（10）.

[25]董元方，李雄飞.一种不平衡数据渐进学习算法.计算机工程，2010，36（24）.

Imbalanced Data;Resample;Cost-Sensitive Learning;Ensemble Technique

Survey of Classification with Imbalanced Data

LI Yuan-ju
（College of Computer Science,Sichuan University,Chengdu 610065）

李元菊（1990-），女，河南人，硕士研究生，学生，研究方向为自然语言处理和数据挖掘

2015-12-08

2016-01-10

在分类领域中，当数据集不平衡时，传统的分类算法和评估指标都不能很好地对数据分类。因此，多年来不少学者针对这一领域进行研究。主要分为三大类，即抽样方法、代价敏感方法、集成方法。同时针对这个领域枚举一些评估指标。

In classification field,when the data is imbalanced,the traditional classification algorithms and evaluation criteria are not good for it.So, a lot of researchers study it recent years.Mainly divides into three categories,such as resample technique,cost-sensitive learning and ensemble techniques.At the same time,puts forward some new standards to evaluate the algorithms in this field.