改良的Manning-Rosen势Schrödinger方程散射态解

陈文利，史艳维，鱼　翔

(西安培华学院通识教育中心，陕西 西安　710125)



·基础学科·

改良的Manning-Rosen势Schrödinger方程散射态解

陈文利，史艳维，鱼翔

(西安培华学院通识教育中心，陕西 西安710125)

对改良的Manning-Rosen势的径向薛定谔方程任意l波散射态进行解析求解，得到按“K/2π标度”的相移公式和归一化的超几何函数表示的径向波函数。通过对散射振幅在极点解析性质的研究得到束缚态能级, 而特征值的数值结果与先前结果的比较进一步验证了本文结果的精确性。

改良 Manning-Rosen势场 ;散射态; 近似解析解

随着量子理论的发展，对于不同势场含有离心项l(l+1)/r2的径向薛定谔方程的求解一直是研究的热点，然而，能够解析求解的势场大多被约束在s(l=0)态。近年来，研究者提出了近似求解方法在大多可解势场中得以应用, 诸如指数近似办法[1]、 Pekeris近似办法[2]和改良的指数近似办法[3]等近似表示离心项。有些近似办法被应用到超几何函数方法[4]中，有些学者利用超对称[5]、形状不变形方法[6]求解薛定谔方程解析解，这些方法进一步地丰富了求解的计算方法。在Manning-Rosen 势基础上,有显著改良 Manning-Rosen 势场被提出来[7]，它的表达式为

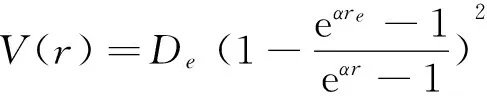
(1)

其中：De是离解能；re是势函数的最小值点； α是可调节的势参数。该势场被广泛的应用于分子物理和化学物理。对于改良Manning-Rosen 势场，Jia等计算了Klein-Gordon方程束缚态解析解[8]、自旋对称的狄拉克方程[9-10]，Oluwadare等计算了魔自旋对称Klein-Gordon和狄拉克[11]，Dong等利用近似办法求解了束缚态解析解，推导出了近似特征值方程[12]；然而散射态的求解一直很少被涉及。在我们先前工作的基础上，本文利用更合适的近似公式求解改良Manning-Rosen 势场散射态波函数解析解，同时，利用散射态波函数渐进行为求出归一化常数N和相移θl的解析表达式。 最后，给定不同的势参数和量子数，数值求解特征值，并和先前求解数据及MATHEMAITC 程序包所得数据进行对比。

1　散射态的近似解析解

含改良Manning-Rosen势的径向薛定谔方程可表示为

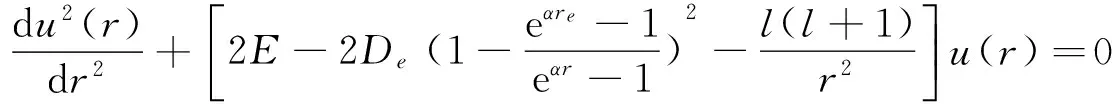
(2)

由于离心项l(l+1)/r2的存在，方程(2)的求解大都被要求在s波(l=0)条件下求解。 像我们先前工作一样[1-2，13]，大多作者提出对离心项做合适的近似，继而将薛定谔方程的求解推广到任意l波。对于改良的Manning-Rosen势本文应用文献[8]中的Greene-Aldrich近似表达式

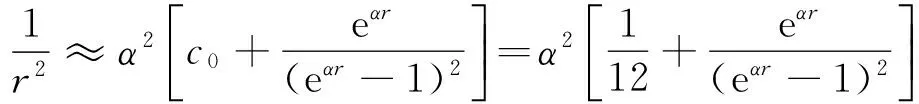
(3)

近似表示离心项，当c0=0时，近似表达式就变成惯用的Greene-Aldrich 近似。将方程(3)代入方程(2)可得

(4)

对上式自变量作指数变换，即引入新变量x=1-e-αr(r∈(0,),x∈(0,1))，并代入方程(4)化简得到量纲一方程

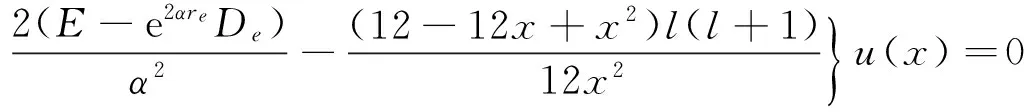
(5)

满足边界条件方程(5)的径向波函数可按“K/2π标度”归一化的超几何函数表示[14-16]。设波函数的形式为

u(x)=(1-x)-ikxδF(x)，

(6)

其中

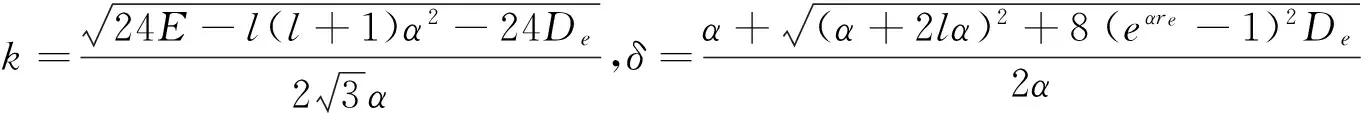
(7)

把方程(6)代入方程(5)可得

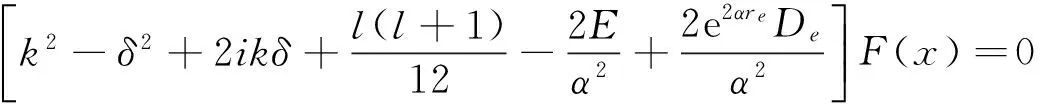
(8)

方程(8)为超几何微分方程，其解可表示为

F(x)=C12F1(a;b;c;x)+C2x1-c2F1(a-c+1;b-c+1;2-c;x)，

(9)

其中参数

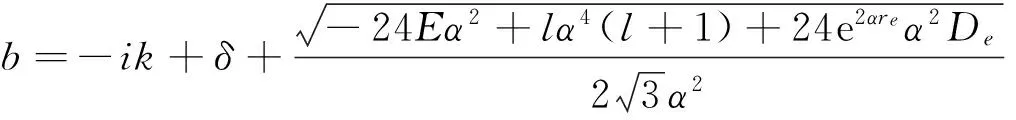
c=2δ。

(10)

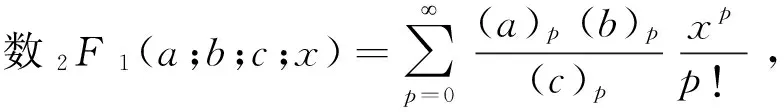
u(r)=N[1-e-αr]δeikαr2F1(a;b;c;1-e-αr),

(11)

其中，N是归一化常数。

下面利用散射态波函数渐进行为确定归一化常数N 和相移θl的解析表达式, 从方程(10)可以得到参数a,b,c满足

(12)

利用超几何函数的变换公式

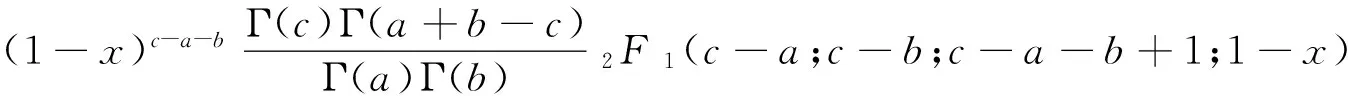
(13)

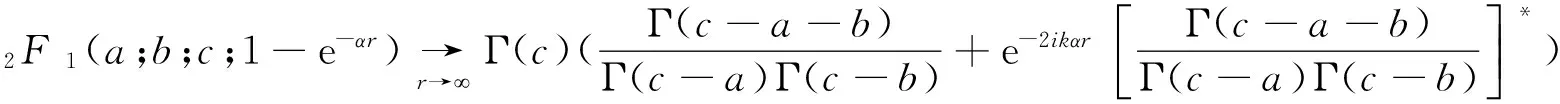
(14)

令

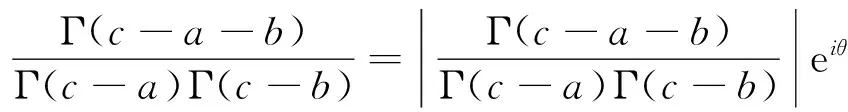
(15)

其中θ为常数。把方程(15)代入方程(14)可得

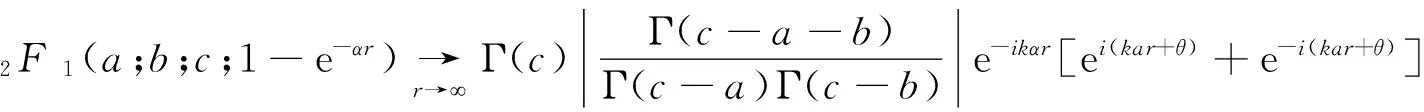
(16)

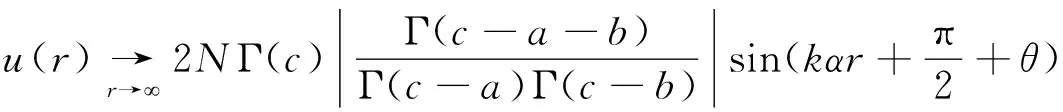
(17)

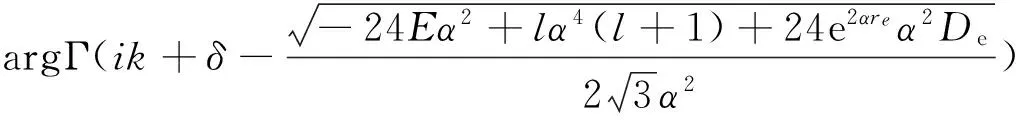
(18)

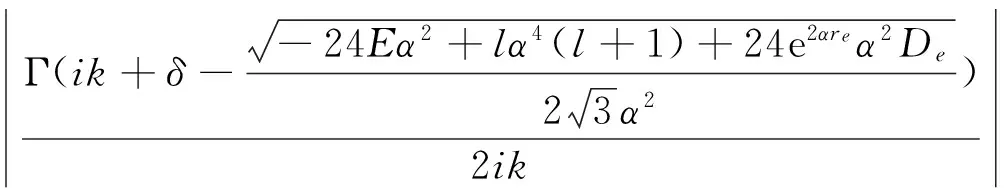
(19)

对于s波(l=0)，离心项l(l+1)/r2等于零；因此，对于改良的Manning-Rosen势s波的归一化常数N0和相移近似解析解θ0，只需取方程(18)、(19)公式中l=0即可得。

根据散射态和束缚态的关系，结合方程(18)中伽马函数的性质，可得

(20)

结合方程(7)，解析求解方程(20)，即得到特征值表达式

(21)

本文求解出的特征值方程(21)和文献[12]中特征值方程(20)化简相应的参数所得的特征值方程本质是相同的。

2　数值结果

为了说明本文结果的精度，把公式(21)计算所得特征值和先前文献[13]中的数值及公认最接近精确值的Lucha,et al程序包所得数据作对比(见表1)。对所得数据进行对比分析可知，本文所得的特征值比先前计算所得数据更好地逼近精确值。

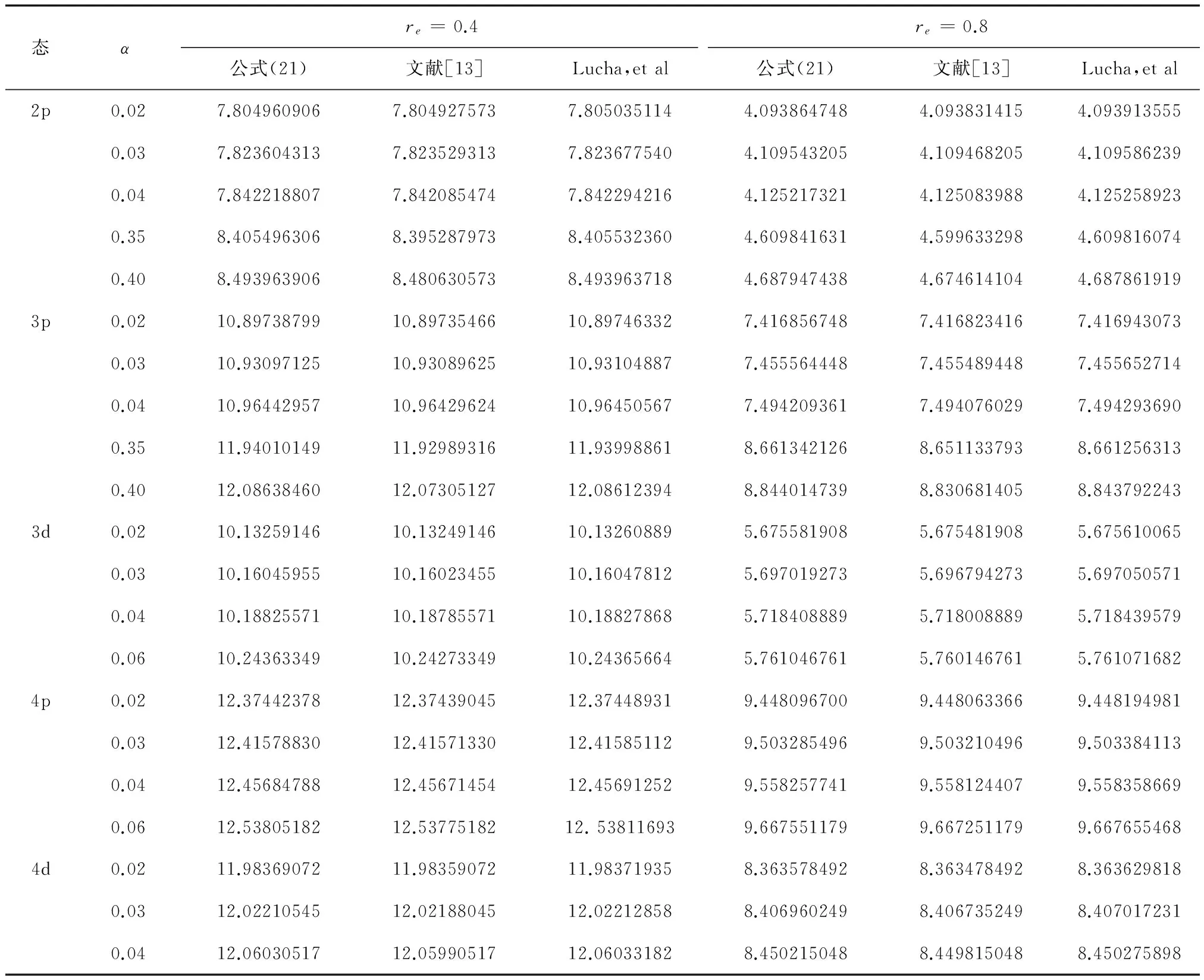
表1　2p, 3p, 3d, 4p, 4d, 4f, 5p, 5d, 5f, 5g, 6d和6f态特征值数值表, 其中势参数取为De=15

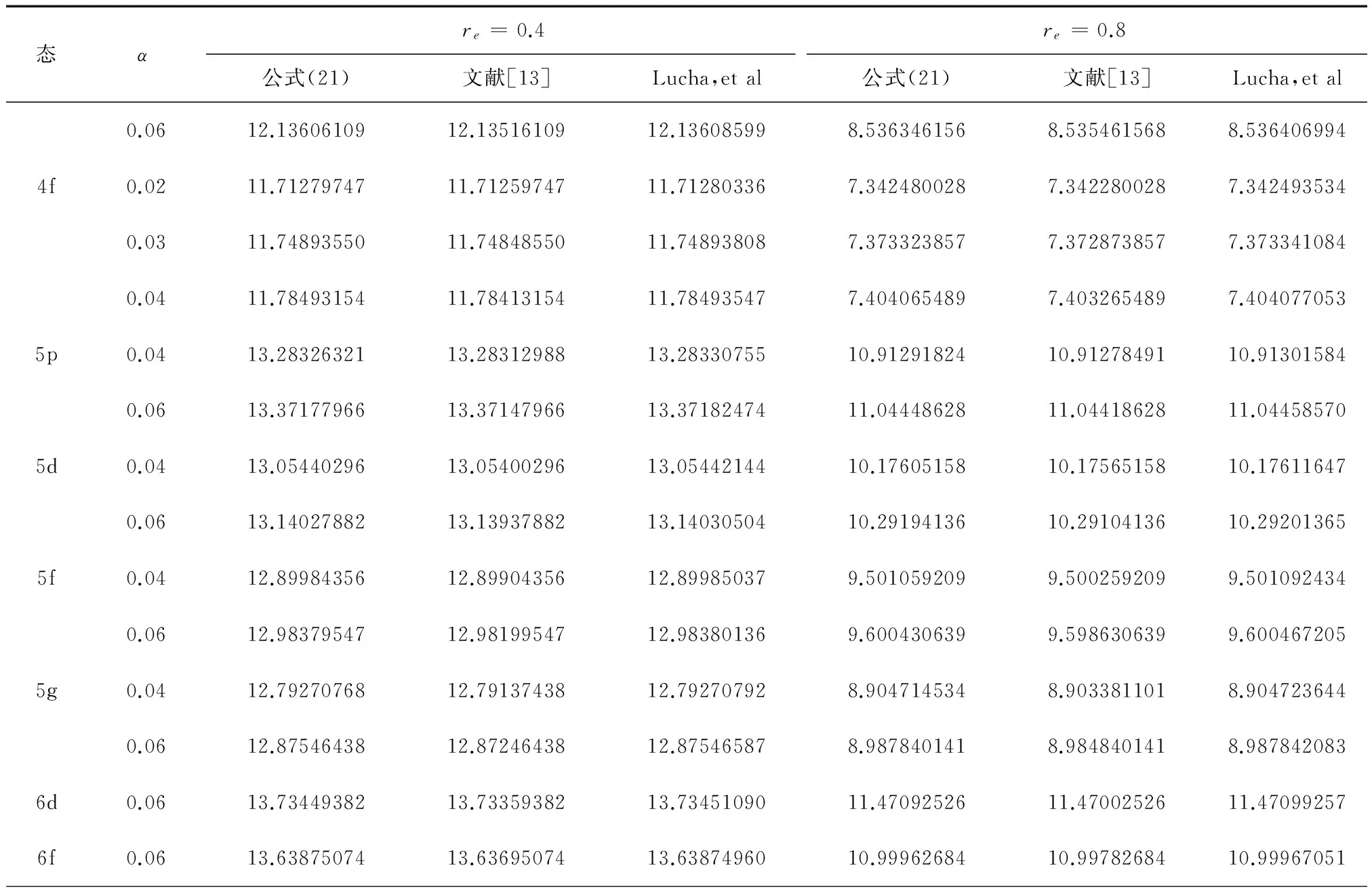
表1(续)

3　结论

对短势场改良的Manning-Rosen势利用合适的近似办法近似表示离心项，求解了任意l波薛定谔方程散射态解析解，得到了相应的相移公式和按“K/2π标度”归一化的超几何函数表示的径向波函数，印证我们所计算出的特征值方程和先前计算出的表达式本质是相同的。为了进一步说明近似精度，我们数值计算了特征值方程，所得的特征值数据较先前数据更好地逼近了MATHEMATICA程序包所得数据。

[1]Wei Gao-Feng, Chen Wen-Li, Wang Hong-Ying, et al. The Scattering States of The Generalized Hulthén Potential with an Improved New Approximate Scheme for The Centrifugal Term[J].Chinese Physics B,2009,18(09):1674.

[2]Qiang Wen-Chao, Chen Wen-Li, Li Kai, et al. The Scattering States of The l-wave Schrödinger Equation with The Second Pöschl-Teller-like Potential[J].Physica Scripta,2009,79:025005.

[3]You Yuan, Lu Fa-Lin, Sun Dong-Sheng, et al. Improved Analytical Approximation to The Scattering Solutions of The Schrödinger Equation with a Hyperbolical Potential[J].Communications in Theoretical Physics,2014,62:315.

[4]Wei Gao-Feng, Long Cha-Yun, Dong Shi-Hai. The Scattering of The Manning-Rosen Potential with Centrifugal Term[J].Physics Letters A,2008,372:2592.

[5]Daniel A Morales. Supersymmetric Improvement of The Pekeris Approximation for The Rotating Morse Potential[J].Chemical Physics Letters,2004,394:68.

[6]Jia Chun-Sheng, Wang Jia-Ying, He Su, et al. Shape Invariance and The Supersymmetry WKB Approximation for a Diatomic Molecule Potential[J].Journal of Physics A: Mathematical and Theoretical,2000,33:6993.

[7]Wang Ping-Quan, Zhang Lie-Hui, Jia Chun-Sheng, et al. Equivalence of The Three Empirical Potential Energy Models for Diatomic Molecules[J].Journal of Molecular Spectroscopy,2012,274:5.

[8]Jia Chun-Sheng,Chen Tao, He Su. Bound State Solutions of The Klein-Gordon Equation with The Improved Expression of The Manning-Rosen Potential Energy Model[J].Physics Letters A,2013,377:682.

[9]Jia Chun-Sheng, Zhang Lie-Hui, Liu Jian-Yi. Stability Analysis of The Solution of The Dirac Equation for The Vibrational Energies of The SiF+ Molecule[J].The European Physical Journal Plus,2016,131:2.

[10]Jia Chun-Sheng, Dai Jian-Wei, Zhang Lie-Hui, et al. Relativistic Energies for Diatomic Molecule Nucleus Motions with The Spin Symmetry[J].Physics Letters A,2015,379:137.

[11]Oluwadare O J, Oyewumi K J, Akoshile C O, et al. Approximate Analytical Solutions of The Relativistic Equations with The Deng-Fan Molecular Potential Including a Pekeris-type Approximation to The(pseudo or) Centrifugal Term[J].Physica Scripta,2012,86:035002.

[12]Dong Shi-Hai, Gu Xiao-Yan. Arbitrary l State Solutions of The Schrödinger Equation with The Deng-Fan Molecular Potential[J].Journal of Physics: Conference Series,2008,96:012109.

[13]Wei Gao-Feng, Chen Wen-Li. Continuum States of Modified Morse Potential[J]. Chinese Physics B,2010,19(9):090308.

[14]曾瑾言.量子力学[M].3版.北京: 科学出版社,2000:547.

[15]陈昌远,陆法林,孙东升. Hulthén势散射态的解析解[J].物理学报, 2007,56(11):6204.

[16]Landau L D,Lifshitz E M .Quantum Mechanics (Non-Relativistic Theory) [M]. 3rd ed. New York: Pergamon Press,1977:122.

(编校：叶超)

The Scattering States of Schrödinger Equataion with the Improved Manning-Rosen Potential

CHEN Wenli, SHI Yanwei, YU Xiang

(GeneralEducationCenter,Xi’anPeihuaUniversity,Xi’an710125China)

We obtianed the scattering state analytical solutions of the Schrödinger equation for the improved Manning-Rosen potential. The explicitly calculation formula of phase shift is derived and the normalized radial wave functions of scattering states on the“K/2π scale” are presented. The energy levels of the bound states are also obtained by studying analytical properties of scattering amplitude. All data calculated by the above approximate analytical formulae are compared with those obtained by the previous. Numerical results show the accuracy of our results.

the improved Manning-Rosen potential; scattering states; approximately analytical solutions

2016-02-12

陕西省教育厅科学研究项目(15JK2093)。

陈文利(1981—)，男，讲师，硕士研究生，主要研究方向为计算物理。

O365

A

1673-159X(2016)04-0039-5

10.3969/j.issn.1673-159X.2016.04.008