基于对立度算法的瓦斯涌出量预测

岳晓光，曹　涌

(1. 武汉大学土木建筑工程学院，湖北 武汉　430072；2. 西南林业大学计算机与信息学院，云南 昆明　650224)



·建筑与土木工程·

基于对立度算法的瓦斯涌出量预测

岳晓光1，曹涌2

(1. 武汉大学土木建筑工程学院，湖北 武汉430072；2. 西南林业大学计算机与信息学院，云南 昆明650224)

为减轻煤矿瓦斯灾害危害，对瓦斯涌出量进行预测具有十分重要的现实意义。为进一步提高预测精度，将对立度算法应用到实际案列中，并与其他预测算法进行对比分析。基于对立度算法的基本原理，构建对立度算法数值计算算子的基本步骤；通过引入煤矿瓦斯数据，对瓦斯涌出量进行了预测；在同等条件下，与采用其他经典方法预测所得结果进行对比。对比结果表明，对立度算法平均误差均小于其他经典方法，最小可低于1%；因此，应用对立度算法应用到瓦斯涌出量预测中可提高预测精度。

对立度算法；瓦斯涌出量；数值计算算子；预测算法

随着煤矿开采强度的增加，瓦斯涌出量会进一步增大，而瓦斯涌出量和瓦斯灾害息息相关；因此，瓦斯涌出量预测预警研究具有十分重要的现实意义。目前，已经有了许多智能预测算法应用到相关领域。其中，智能算法及其改进算法非常多，常见的有遗传规划、神经网络、遗传算法、支持向量机、粗糙集、模糊聚类等方法。为了进一步提高预测精度，本文引入对立度(opposite degree，OD)算法。对立度算法是一种新的算法，在多因素预测分析中已经有了部分应用，且取得了较好的效果[1-2]；因此，本文研究重点是将对立度算法数值预测应用到实际案例中，主要包括以下几个步骤：首先，构建对立度算法数值计算算子；其次，采用数值计算算子预测瓦斯涌出量；最后，分析相关预测结果。

1　对立度算法

对立度算法是一种基于对立度计算的新算法，目前已经应用在了金属磨损安全[1]、材料稳定性[2]、软土地基沉降[3]、煤矿工程数据处理[4]等方面。

对立度(opposite degree，OD)主要涉及以下3个基本信息。

1.1先验数值

先验数值是指已用于训练学习的数值。先验数值是已经事先获得的数值。

1.2后验数值

后验数值是指用来预测分析的数值。后验数值是一组和先验数值具有一定关联性的数值。

1.3数值的对立度计算

对立度表示先验数值和后验数值之间差别的程度，取值范围是(-,+)。

一般情况下，定义先验数值是A，后验数值是B，称为B相对于A的对立度，简称为对立度，记为O(A,B)，如下所示：

其中：O越趋近于0，B和A越接近；O等于0时，A和B相等。

2　数值计算算子构建

已知，一个先验矩阵

其对应的先验数值列向量是

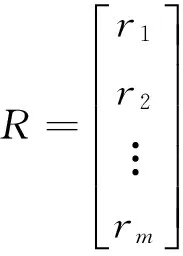
对立度算法可以通过矩阵运算进行数值预测，由于篇幅有限，则数值计算算子的主要步骤如下所示。

2.1求训练样本的对立度数据

对立度矩阵Oi(1≤i≤m)表示Am×nR的第i行数据与Am×nR的m行数据进行对立度计算所得的对立度矩阵，即计算矩阵Am×nR每行与其他行的对立度。其中，Am×nR是由Am×n和R组成的矩阵，具有m行、n+1列。对立度矩阵计算公式如下：

(1)

2.2求权重

求权重wi。wi表示第i行对应到每个数据项(aij)的权重。

1)删除掉Oi中值为全0的行(由对立度的性质可知，矩阵存在全0的行)，得到OD。这OD个矩阵可以组成矩阵O′。

2)剔除最后一列作为预测值的参考值，得到O″。

3)求绝对值。由于权重表示aij的重要程度，这里全部取正值。

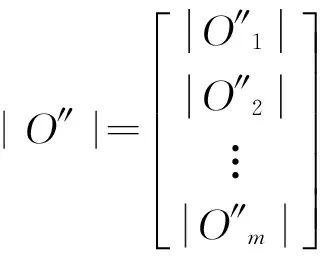
(2)

5)求权重。先求平均值的倒数，然后求和，最后用倒数除以总和得到权重。其中，wi为每一列的权重。如公式3所示：

(3)

2.3求预测数据的对立度计算

2.4求测试样本的对立度平均值及加权对立度之和

…

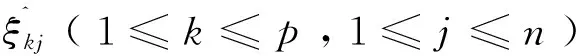
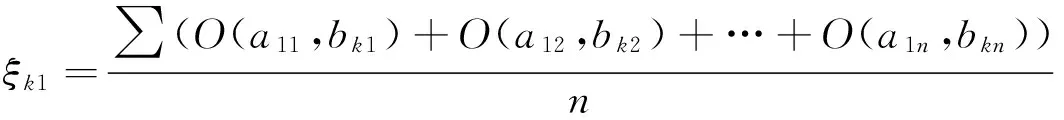
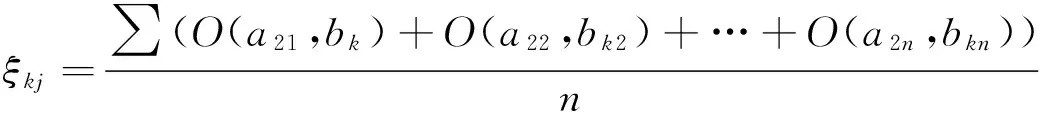
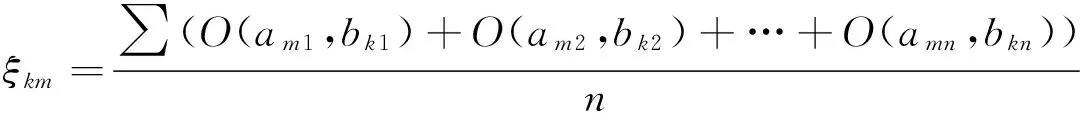
(4)

…

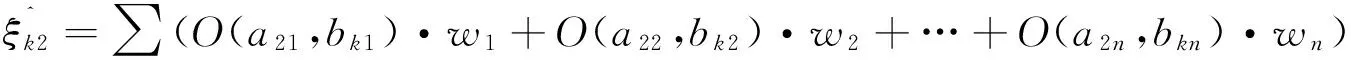
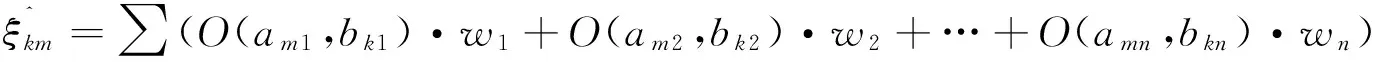
(5)

2.5求备选数据行

βkj=min(|O(a1n,bkn)|,

|O(a2n,bkn)|,…,|O(amn,bkn)|)

(6)

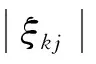
2.6求绝对差值

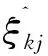
(7)

同时，为了控制γk的误差，应设置绝对差值控制阈值y，如果γk大于y，则算法需要考虑从min(γk)(γk最小)对应的数据行中选择合适的数据。

2.7确定计算的依据行

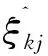
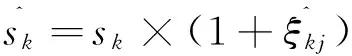
(8)

2.8求预测值

重复步骤2.1到2.7，直到求出预测的数值矩阵，如下式所示。

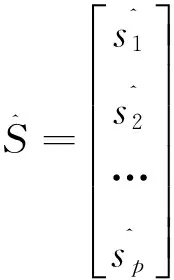
(9)

3　瓦斯涌出量数值预测实验

为了验证算法数值预测的有效性，选取某矿的一部分瓦斯监测数据[5-6]，如表1所示。N代表序号，A代表煤层深度(m)，B代表煤层厚度(m)，C代表煤层瓦斯含量(m3·t-1)，D代表煤层间距(m)，E代表日进度(m·d-1)，F代表日产量(t·d-1)，G代表绝对瓦斯涌出量(m3·min-1)；煤层深度、煤层厚度、煤层瓦斯含量、煤层间距、日进度、日产量等都是影响瓦斯涌出量的主要因素。为了验证算法稳定性(可重复性)，这里采用2组实验。其中，实验一是学习前15组，预测后3组；实验二是学习前13组，预测后5组。

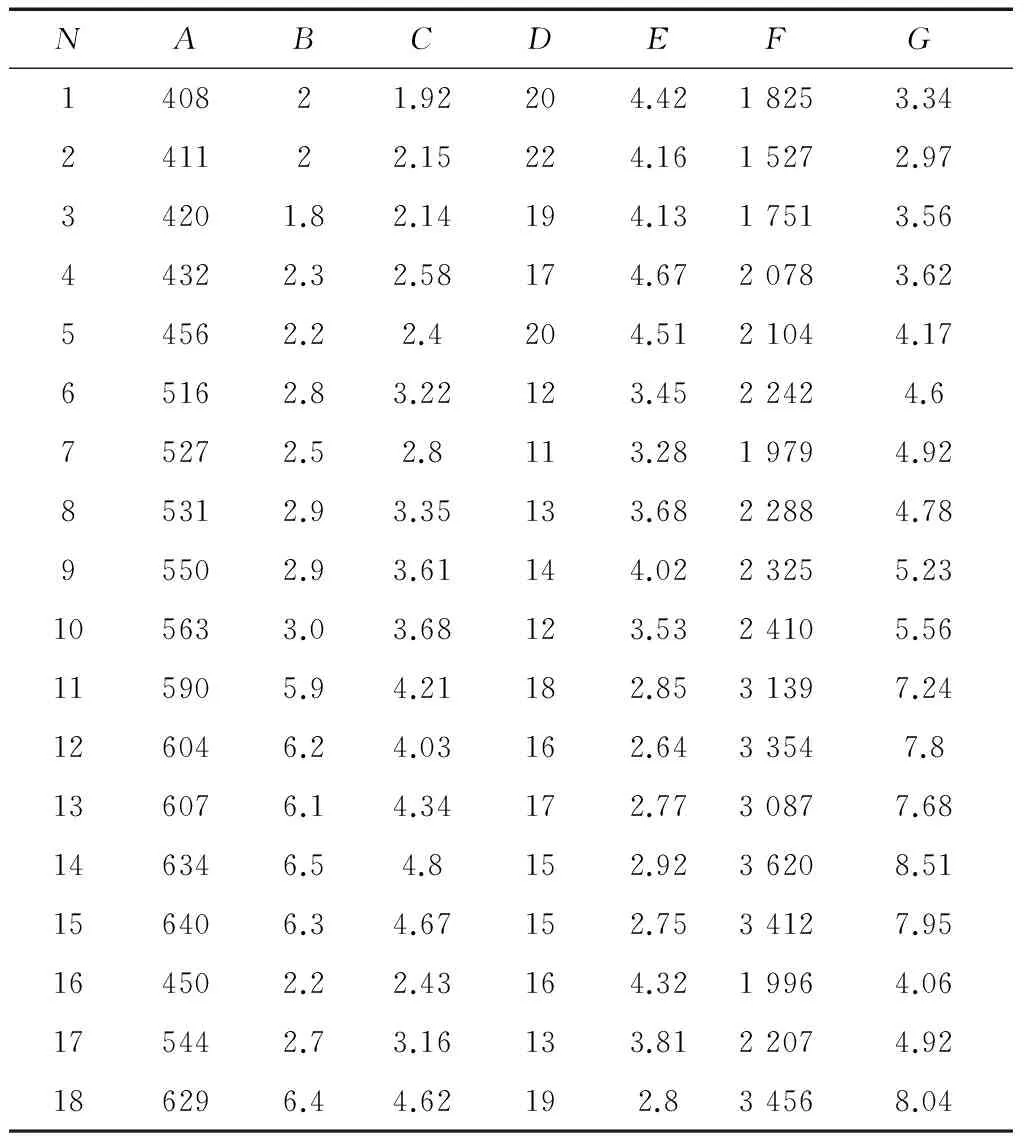
表1　实验样本

3.1实验一

实验一选择前15组(表1中第1至15行)数据为训练样本，后3组(表1中第16至18行)数据为测试样本。

3.1.1确定计算的依据行

根据第2部分的计算步骤，可以获取备选数据，从备选数据里面选择绝对差值最小的那行作为近似值计算的依据行，选定依据行对应的值用于求预测值。3组预测数据的依据行如表2所示。

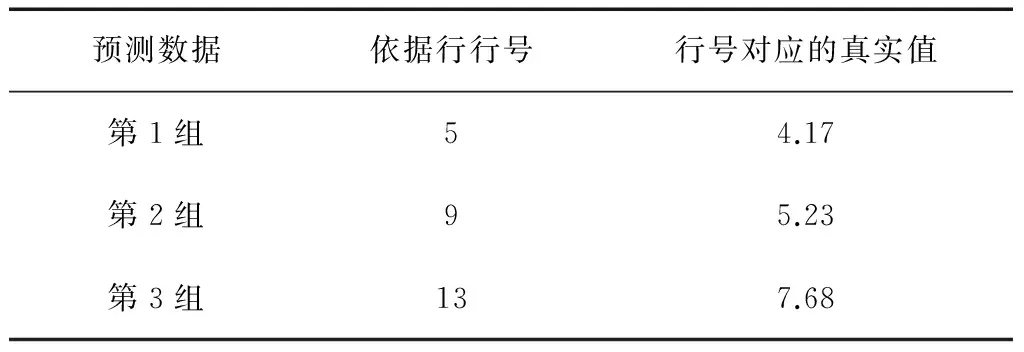
表2　预测数据的依据行数据

3.1.2求预测值

采用公式(8)和式(9)，求出所有的预测值，如表3所示。

表3　预测值

3.2实验二

考虑到不同的训练样本和测试样本比例的情况，预测结果精度的偏差可能会比较大。实验二选择前13组(表1中第1至13行)数据为训练样本，后5组(表1中第14至18行)数据为测试样本。计算步骤同实验一，具体计算过程不再赘述。预测结果如表4所示。

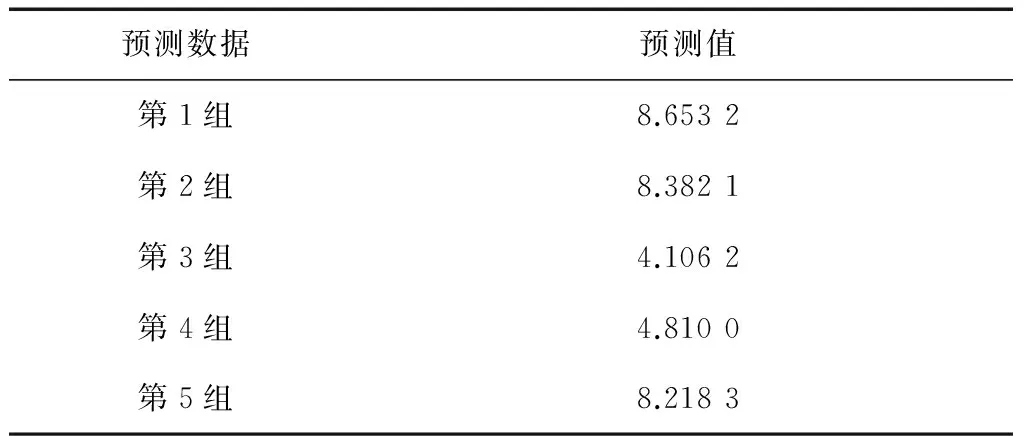
表4　预测值

4　结果分析

下面分别对两组实验进行分析。

4.1实验一的结果分析

为了对OD算法的预测精度进行评估，引用文献[5-9]中的几种方法的预测结果与OD算法进行比较分析(均基于表1中的数据)。同时，这些文献中采用的有同样的模型，但是由于各种参数设计的不同，导致结果并不相同。另外，考虑到不同参数设置情况下的同一种方法之间的比较仍然具有一定意义，因此，这里把不同文献下的同样方法分别命名。

文献[5]采用神经网络的方法，简称为方法一；文献[6]采用GP(genetic programming，遗传规划)的方法，简称为方法二；文献[7]采用神经网络和BP-GA(back propagation-genetic algorithm，BP神经网络与遗传算法结合)的方法，分别简称为方法三、方法四；文献[8]采用神经网络方法，简称为方法五；文献[9]采用SMO-M5P(sequential minimal optimization-M5-prime，序贯最小优化与M5模型树结合)、SMO[10]、M5P[11]、神经网络等4种方法，分别简称为方法六、方法七、方法八、方法九。各种方法及OD算法之间的预测结果比较如图1所示。

方法一是神经网络方法，采用的是较为常见的BP(back propagation)网络模型。方法二是遗传规划算法，通过随机生成初始群体、计算个体适应度、选择最佳个体等步骤进行计算，最终得到新一代的群体(计算结果)。方法三、方法五、方法九仍然是神经网络方法，但是，考虑到其参数设置等细节不同(从预测结果可以反映这方面的设置问题)，这里也将他们引入进行比较。方法四是BP-GA方法，即通过BP神经网络与遗传算法结合，采用遗传算法优化BP神经网络的权值和阈值，改进收敛速度和预测结果。方法七是SMO回归模型，是由Shevade等[10]提出的；方法八是M5P回归模型，是由Wang等[11]提出的；而方法六是将二者结合，即序贯最小优化与M5模型树结合的算法，分别通过SMO回归模型和M5P回归模型进行预测，然后计其平均值为目标值进行预测。

其中，方法一、方法二、方法三、方法四、方法五、方法六、方法七、方法八、方法九、OD算法的预测结果(预测值及平均相对误差)分别如表5—14所示。

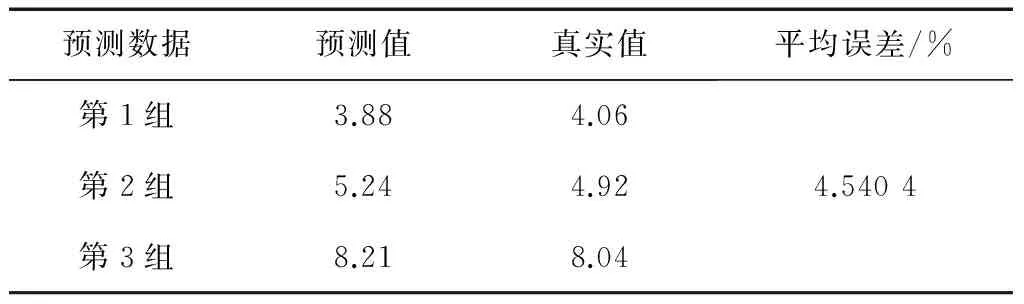
表5　方法一预测结果

表6　方法二预测结果

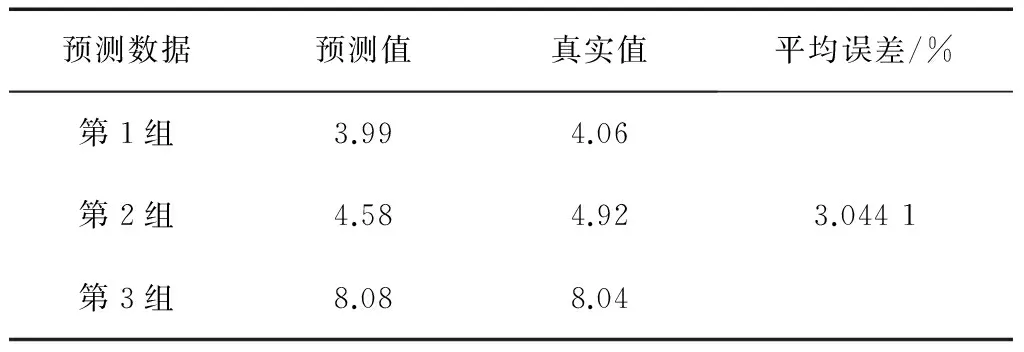
表7　方法三预测结果

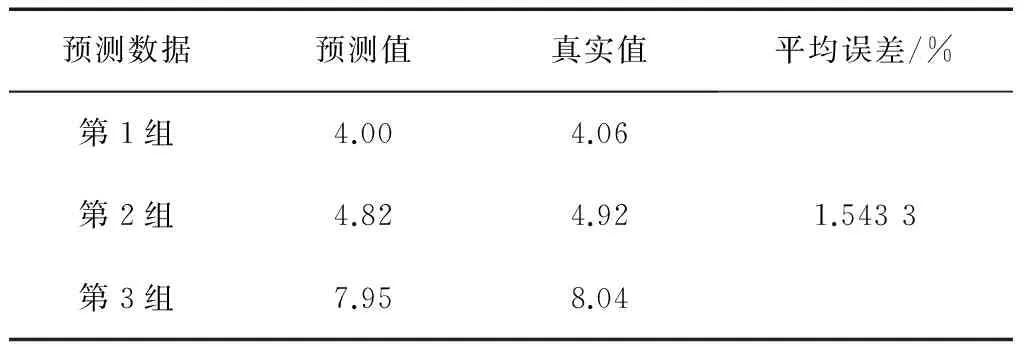
表8　方法四预测结果

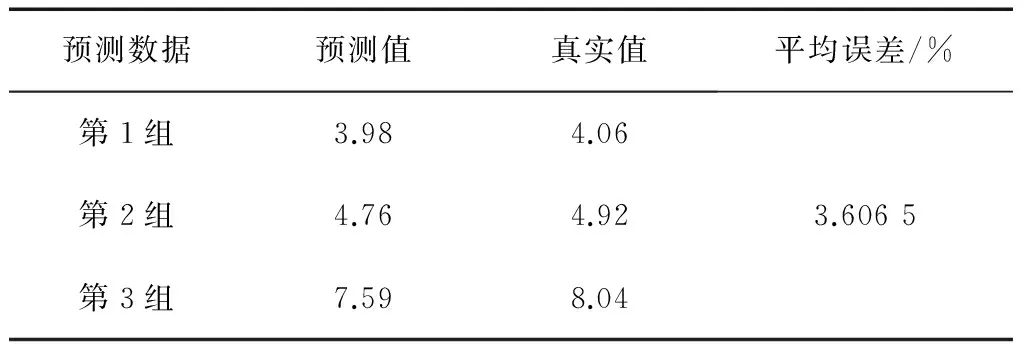
表9　方法五预测结果

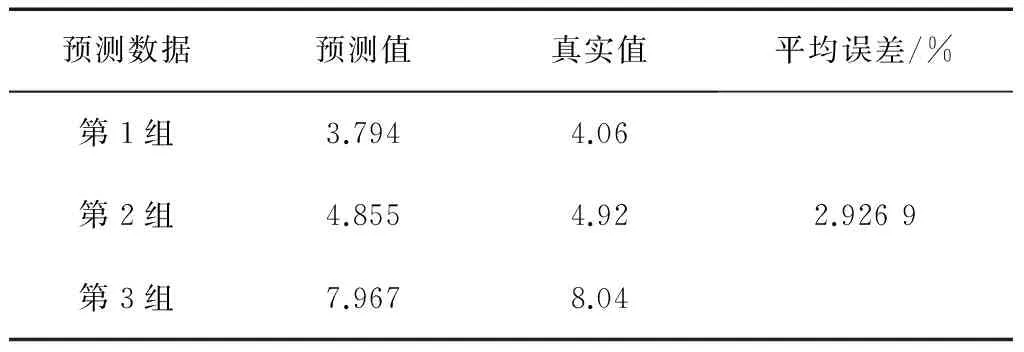
表10　方法六预测结果

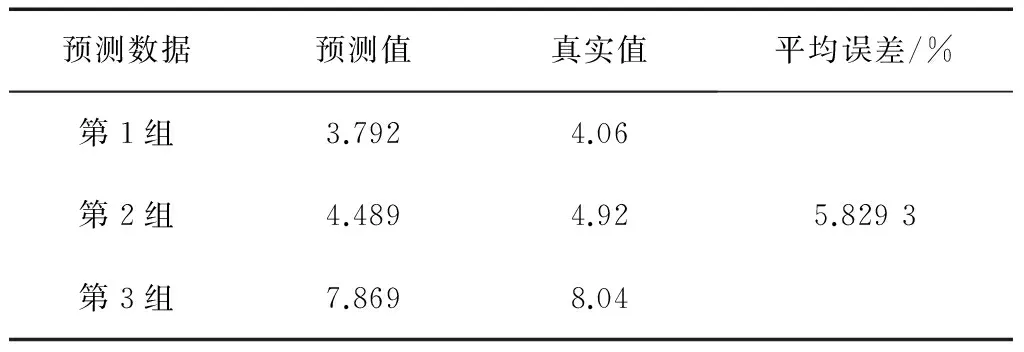
表11　方法七预测结果

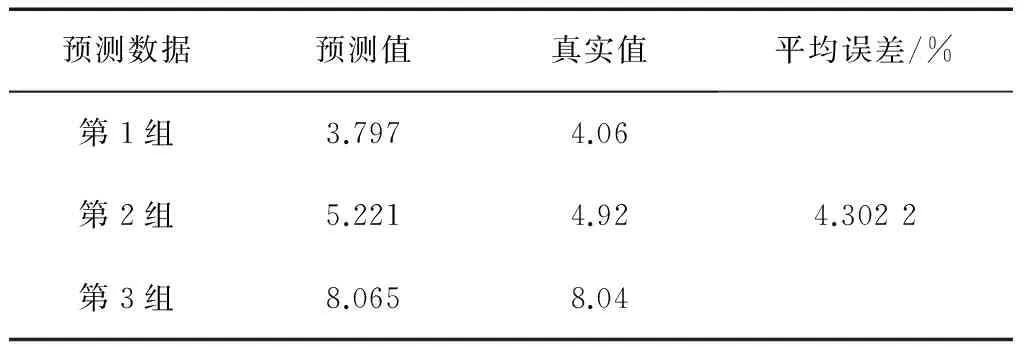
表12　方法八预测结果

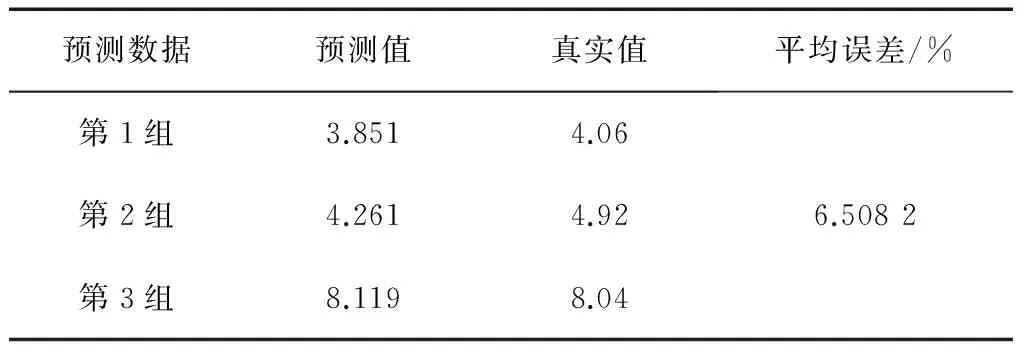
表13　方法九预测结果

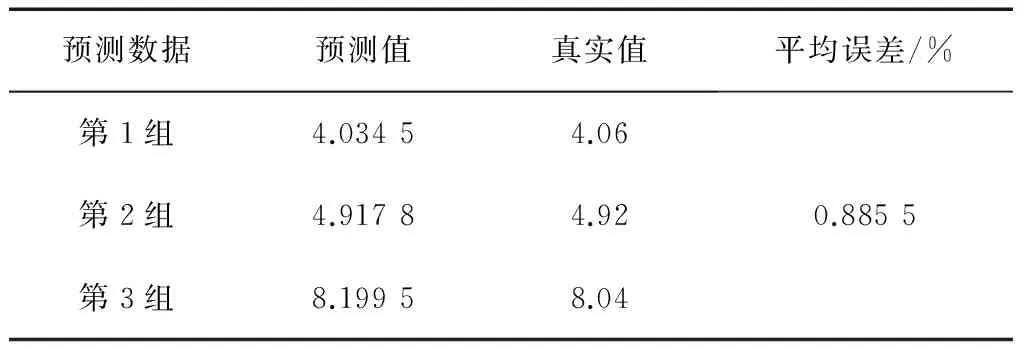
表14　OD算法预测结果

从图1可以明显看出，OD算法的预测值在平均误差上是最小的，低于1%。

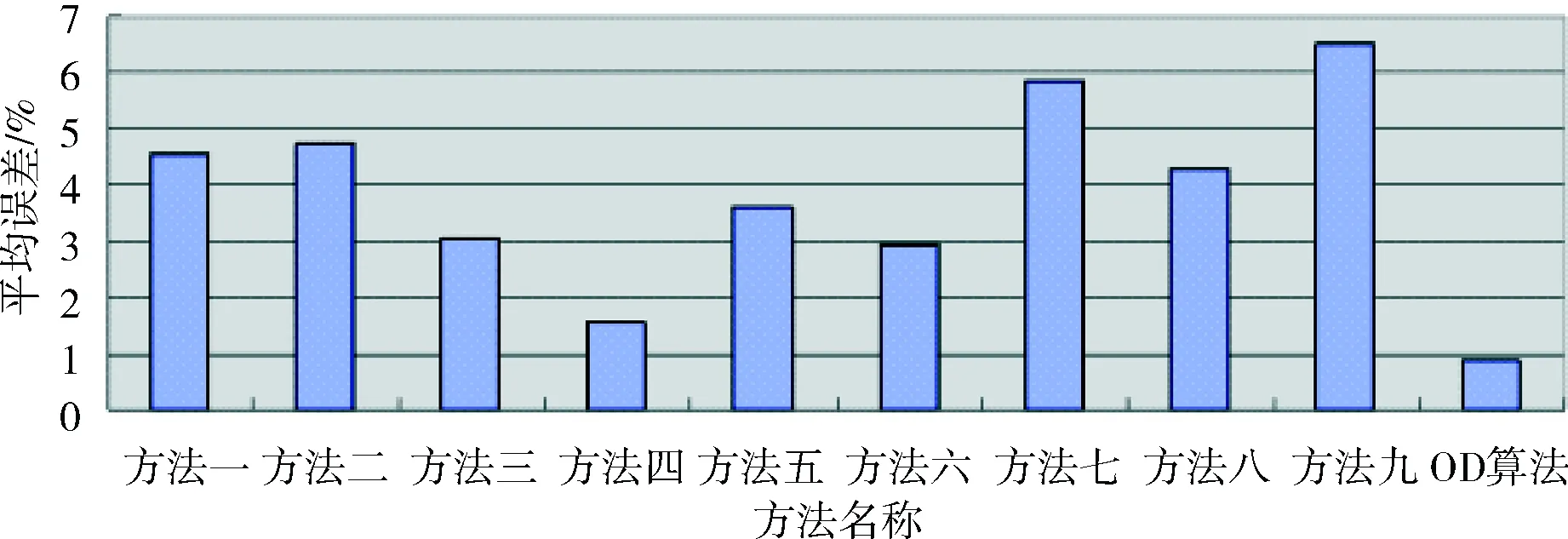
图1　10种方法在平均误差上的比较

综上所述，实验一初步表明了OD算法在数值预测精度方面具有明显的优势，初步验证了OD算法的数值预测适应性。

4.2实验二的结果分析

为了从另外一个角度与OD算法的预测精度进行比较分析，引用文献[9]、文献[12]、文献[13]中的几种方法的预测结果与OD算法进行比较分析(均基于表1中的数据)。

文献[9]采用SMO-M5P、SMO、M5P、神经网络等4种方法，分别简称为方法一、方法二、方法三、方法四；文献[12]采用基于模糊粗糙集与支持向量机的方法，简称为方法五；文献[13]采用SVM(support vector machine，支持向量机)、基于模糊聚类和SVM结合的方法，分别简称为方法六、方法七。各种方法的预测结果比较如表15至表22所示。

表15　方法一预测结果

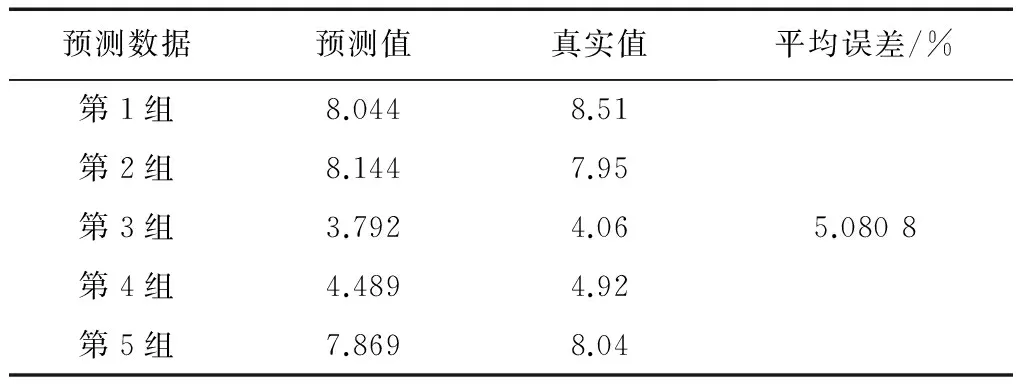
表16　方法二预测结果

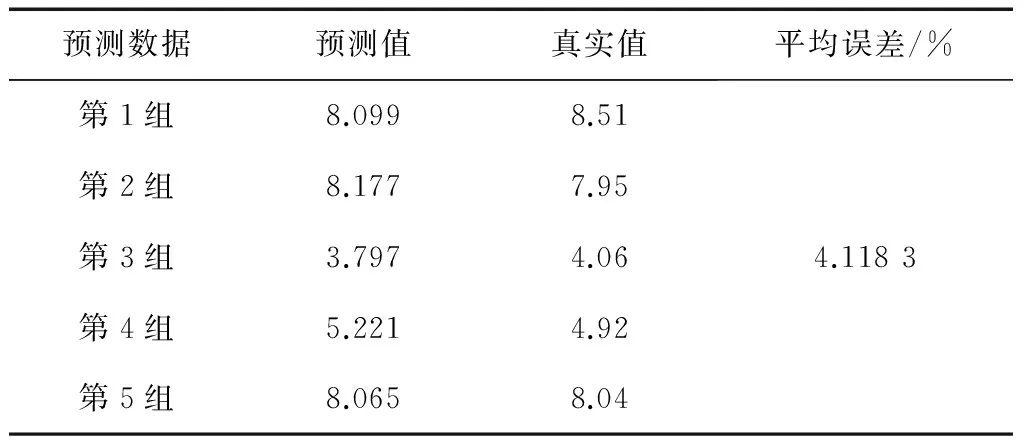
表17　方法三预测结果

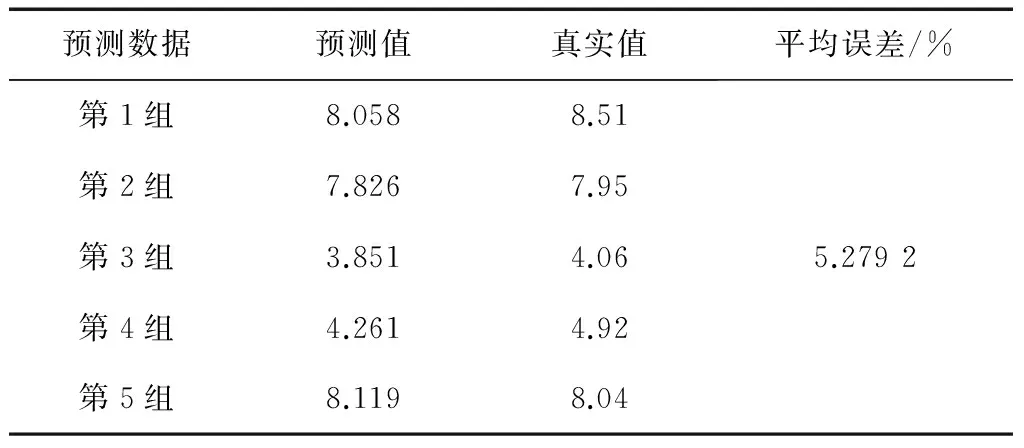
表18　方法四预测结果

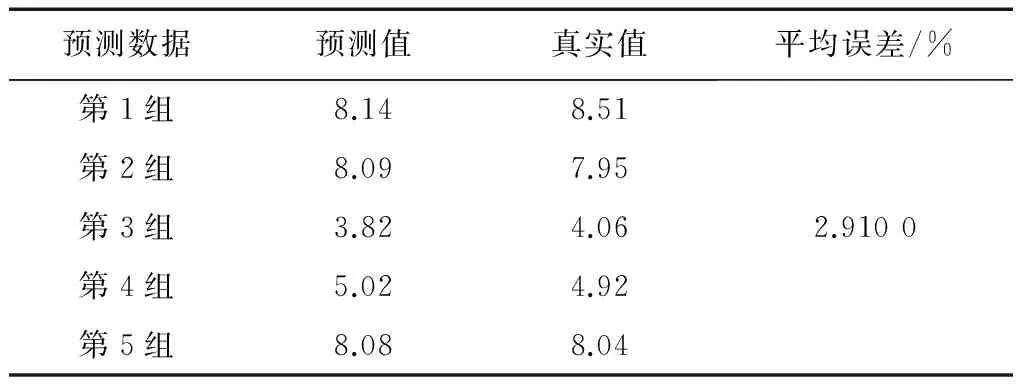
表19　方法五预测结果

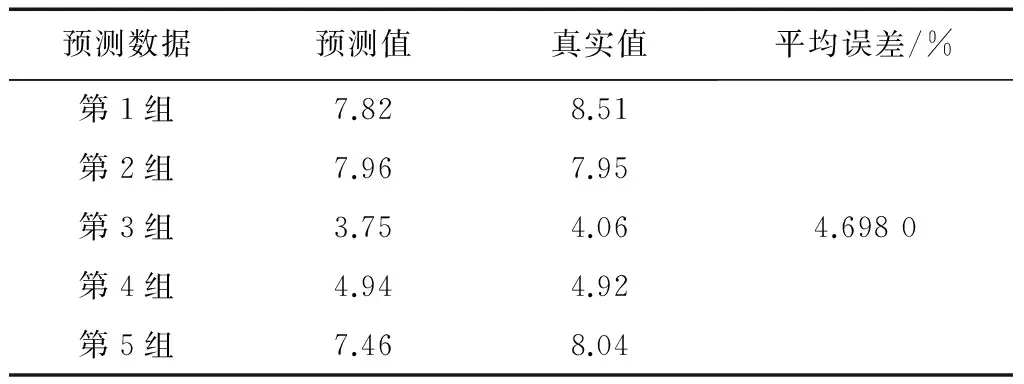
表20　方法六预测结果

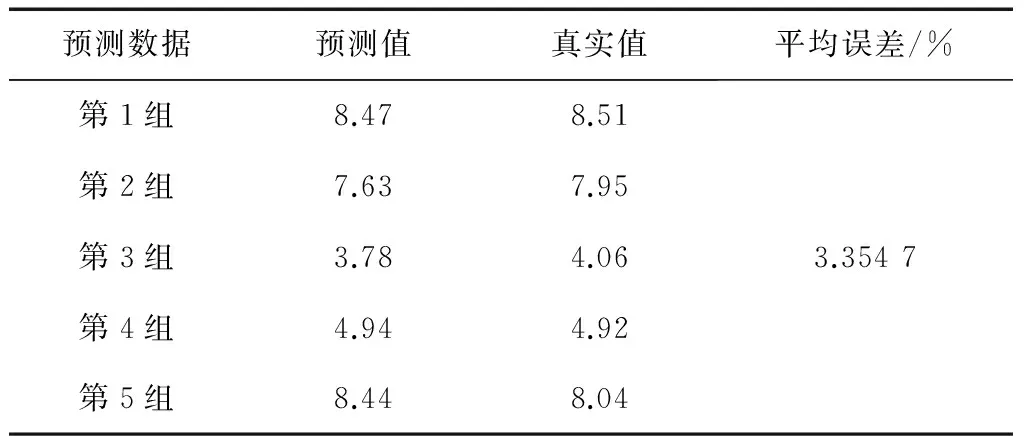
表21　方法七预测结果

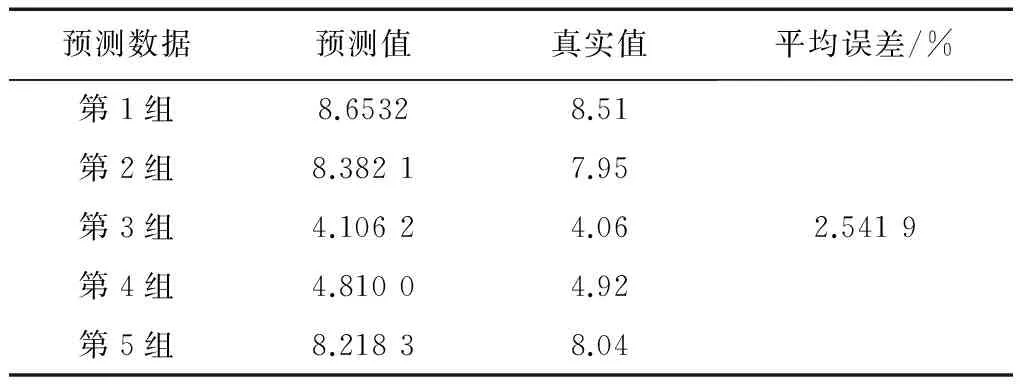
表22　OD算法预测结果

各种方法及OD算法之间的预测结果比较如图2所示。

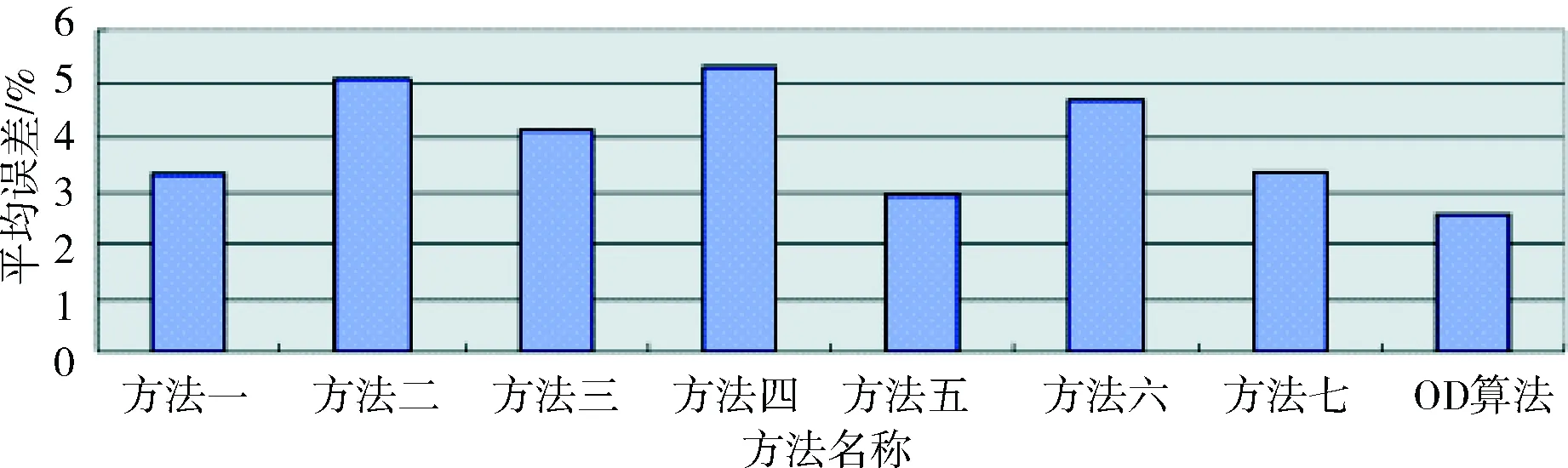
图2　8种方法在平均误差上的比较

可以明显看出，OD算法在平均误差上是最小的，明显低于3%。

综上所述，实验二进一步表明了OD算法在数值预测精度方面具有明显的优势，进一步验证了OD算法的数值预测适应性。

5　结论

对立度算法预测过程可重复，且其原理及模型已经应用到了金属磨损[1]、材料稳定性[2]、地基沉降[3]、矿山安全[4]等多个方面，是一种计算稳定的预测方法。基于OD算法的基本原理，通过计算数值之间对立度，设计具体的数值计算算子，从而达到数值预测的目的。同时，为了初步验证算法的有效性，采用瓦斯涌出量数据，运用OD算法的数值计算算子进行数值预测，其预测结果正确率高，具有较强的实用性。在瓦斯涌出量数值预测的实验一中，OD算法明显优于做比较的其他9种方法；OD算法的平均误差控制在了1%以内，低于其他9种方法。在瓦斯涌出量数值预测的实验二中：OD算法明显优于做比较的其他7种方法；OD算法的平均误差控制在了3%以内，低于其他7种方法。因此，OD算法在煤矿瓦斯涌出量的数值预测上具有可行性和有效性。未来进一步的工作重点是优化其参数设计，并且将该算法应用到更多领域的实证研究。

[1]Xiao Guang Yue, Guang Zhang, Qu Wu, et al. Wearing Prediction of Stellite Alloys Based on Opposite Degree Algorithm [J]. Rare Metals, 2015, 34(2): 125.

[2]Guang Zhang, Xiao Guang Yue, Fei Li, et al. Partially Stabilised Zirconia Stability Prediction Based on Opposite Degree Algorithm for Safety Engineering [J]. Materials Research Innovations, 2015, 19(S2): 671.

[3]Shun Zhou, Xiao Guang Yue. Soft Soil Foundation Settlement Prediction and Economic Cost Management Analysis based on New Algorithm [C]// Proceedings of the ICEMCS. Shenyang:[s.n.], 2015, 17: 395.

[4]Wang XueChen, Yue XiaoGuang, Mostafa Ranjbar, et al. Opposite Degree Algorithm and Its Application in Engineering Data Processing [J]. Computer Modelling and New Technologies, 2014, 18(11): 482.

[5]朱川曲. 采煤工作面瓦斯涌出量预测的神经网络模型 [J]. 中国安全科学学报, 1999, 9(2): 42.

[6]赵朝义, 袁修干, 孙金镖. 遗传规划在采煤工作面瓦斯涌出量预测中的应用 [J]. 应用基础与工程科学学报, 1999, 7(4): 387.

[7]李洪彪. 基于BP神经网络的瓦斯涌出量预测的研究 [D]. 昆明: 昆明理工大学, 2008.

[8]刘健, 刘泽功, 马俊枫. 基于神经网络的矿井瓦斯涌出预测系统及应用研究 [J]. 煤炭技术, 2008, 27(11): 71.

[9]李超群, 李宏伟. 一种基于支持向量机和模型树的回归模型及其在采煤工作面瓦斯涌出量预测中的应用 [J]. 应用基础与工程科学学报, 2001, 19(13): 370.

[10]Shevade S K, Keerthi S S, Bhattacharyya C, et al. Improvements to the SMO Algorithm for SVM Regression [J]. IEEE Transactions on Neural Networks, 2000,11(5)：1188.

[11]Wang Yong, Ian H Witten. Induction of Model Trees for Predicting Continuous Classes [C]// Proceedings of the Poster Papers of the European Conference on Machine learning. Prague:Czech Republic, 1997:128.

[12]任晓奎, 侯洪涛, 江海朋. 基于模糊粗糙集与支持向量机的瓦斯涌出量预测研究 [J]. 计算机测量与控制, 2012, 20(9): 2369.

[13]王晓路. 基于模糊聚类和PQN的瓦斯涌出量预测 [J]. 煤炭技术, 2011, 30(9):93.

(编校：叶超)

Prediction of Gas Emission Based on the Opposite Degree Algorithm

YUE Xiaoguang1, CAO Yong2

(1.SchoolofCivilEngineering,WuhanUniversity,Wuhan430072China;2.SchoolofComputerandInformation,SouthwestForestryUniversity,Kunming650224China)

In order to reduce the hazard of coal mine gas disaster, it is very important to predict the quantity of gas emission. In order to improve the prediction accuracy, the contrast algorithm was applied to the actual case, and compared with other prediction algorithms. Based on the basic principle of opposite degree algorithm, opposite degree algorithm numerical operators were constructed. Through the introduction of coal mine gas data, the gas emission was predicted; and the prediction results were compared under the same conditions with other classical methods. The comparison results show that the average relative error of the algorithm is less than other classical methods, and the minimum error is less than 1%. Therefore, the application of the algorithm can be applied to the prediction of gas emission, which can improve the prediction accuracy.

opposite degree algorithm; gas emission; numerical operator；prediction algorithm

2016-01-18

国家自然科学基金(51404178，51404179，61363061)。

岳晓光(1986—)，男，讲师，博士，博士后，主要研究方向为岩土工程、安全工程。

TP301.6；TD712+.5；X936

A

1673-159X(2016)04-0051-6

10.3969/j.issn.1673-159X.2016.04.011