An Efficient Construction of Secure Network Coding

ZHANG Jing-li，TANG Ping，MA Song-ya

（1.School of Science，Henan University of Technology，Zhengzhou 450001，China；2.School of Mathematics and Statistics，Henan University，Kaifeng 475004，China）



An Efficient Construction of Secure Network Coding

ZHANG Jing-li1，TANG Ping2，MA Song-ya2

（1.School of Science，Henan University of Technology，Zhengzhou 450001，China；2.School of Mathematics and Statistics，Henan University，Kaifeng 475004，China）

Under the assumption that the wiretapper can get at most r（r＜n）independent messages，Cai et al.showed that any rate n multicast code can be modified to another secure network code with transmitting rate n-r by a properly chosen matrix Q-1.They also gave the construction for searching such an n×n nonsingular matrix Q.In this paper，we find that their method implies an efficient construction of Q.That is to say，Q can be taken as a special block lower triangular matrix with diagonal subblocks being the（n-r）×（n-r）and r×r identity matrices，respectively.Moreover，complexity analysis is made to show the efficiency of the specific construction.

secure network coding；global encoding kernel；local encoding kernel；wiretap；block lower triangular matrix

2000 MR Subject Classification:90B18

Article ID:1002—0462（2016）01—0060—09

Chin.Quart.J.of Math.

2016，31（1）：60—68

§1.　Introduction

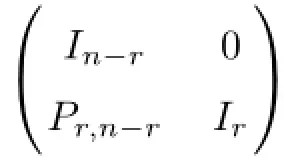
This paper is organized as follows.In the next section，we give the preliminaries that include CSWN model and some notations.Section 3 presents our main results which supply an efficient construction to transform a linear network code to a secure network code.Furthermore，in view of the specific construction of secure network coding，the complexity analysis is made to show its efficiency.In section 4，an example is given to illustrate the result and the last section concludes this paper.

§2.　Preliminaries

A communication network is represented by an acyclic directed graph G=（V，E），where V is the set of nodes and E is the set of edges.Each edge in E represents a communication channel.Assume that all the channels are noiseless and have unit capacity.Denote s as the unique source node and U⊂V as a set of user nodes.A user node is fully accessed by a legal user who is required to receive the random message with zero error.The set of incoming edges and outgoing edges of node t are represented by In（t）and Out（t），respectively.Denote tail（e）=t if e is an outgoing edge of node t and head（e）=t if e is an incoming edge of node t.While the source transmits information across the network at the rate ω，we install a set of incoming imaginary edges at s.A pair of edges（d，e）is called an adjacent pair when there exists a node t with d∈In（t）and e∈Out（t）.A sequence of edges e1，e2，···，enform a path if（ei，ei+1）is an adjacent pair for all 1≤i≤n-1，where e1may be the imaginary channel. Two paths are edge-disjoint if they do not have any edge in common.

Li et al［8］proved that linear network coding can achieve the max-flow bound of multicast. Linear network coding has been widely studied due to its simple structure and desirable properties.In this paper，we mainly discuss linear network coding and adopt the terminologies in Ref.［9］.The global description of a linear network code is described as follows.

Definition 1［9］Let Fqbe a finite field and ω be a positive integer.An ω-dimensional Fq-valued linear network code on an acyclic communication network consists of a scalar kdefor every adjacent pair（d，e）in the network as well as an ω-dimensional column vector fefor every edge e in the network such that：

（ii）The vectors fefor imaginary channels e∈In（s）form the standard basis of the vector space

The vector feis called the global encoding kernel for the edge e，the local encoding kernel at the node t refers to the|In（t）|×|Out（t）|matrix Kt=［kde］d∈In（t），e∈Out（t）.

Let the transmission alphabet be a finite field Fq.In other words，a symbol in Fqcan be transmitted on each channel in the network.Let the source generate a message x in the form of an ω-dimensional row vector.A node receives the symbols x·fd，d∈In（t），from which it calculates the symbol x·fefor sending onto each edge e∈Out（t）via the linear formula

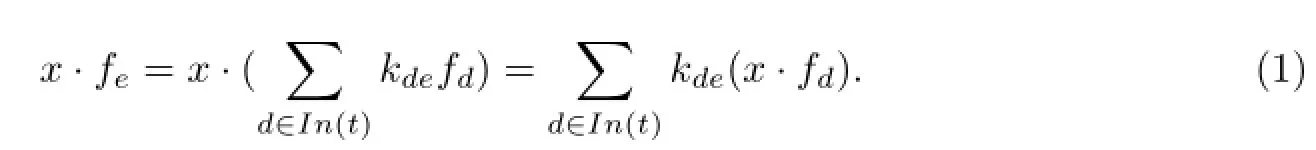
In the following，we introduce the model of a communication system on a wiretap network，and secure or admissible network codes for a wiretap network［2，7］.

A wiretap network consists of a network and a collection of sets of wiretap edges.A is a collection of subsets of the edge set E.Each member of A may be fully accessed by a wiretapper，but no wiretapper may access more than one member of A.In order to ensure the wiretapper obtain no information about the messages transmitted in the network，the transmission must be randomized.Assume that the wiretapper knows the coding scheme and may choose a wiretap subset.

For the given network code，let M be the message and K be the independent random key generated by the source s.Here，we assume that both the source message and the random key have the uniform distribution.Let X=（M，K），then the random output of a wiretap subset A is x·fe，e∈A.Let Yebe the symbol transmitted on the channel e.For a subset B of E，let YB=｛Ye：e∈B｝.We use〈·〉to denote the linear span of a set of vectors and let

A code is said to be decidable if any two message are distinguishable at every user node. A code for a CSWN is said to be secure if a wiretapper can not obtain any information about the secure message by accessing any wiretap subset A.A code for a CSWN is admissible if it satisfies both decidable condition and secure condition.

§3.Main Results

Assume there exists an n-dimensional linear network code over Fqsuch that for all the user nodes u∈U，dim（Vu）=n and for all the wiretap sets A∈A，dim（VA）≤r.Let the multicast message be（m，k）with|m|=n-r and|k|=r.Cai et al［2，7］have proved that a linear network code can be turned into a linear admissible network code by Q-1over Fqand given the construction method for searching the matrix Q.

In this section，we prove that such a nonsingular matrix can be chosen to have the simple form.It implies the specific construction of secure network coding.Then the complexity analysis is given to show the efficiency of the specific construction.

3.1 A Specific Construction of Secure Network Coding

be a maximally independent set of the vectors in｛fe，e∈A｝.Denote

be the corresponding global encoding kernels in the image code，whereIt can be easily seen that for any A∈A，ε1，···，εn-r，are linearly independent is a necessary and sufficient condition for the network code to be secure when both the source message and the random key have the uniform distributions［2，7］.Here，εjdenotes the ndimensional unit column vector whose j-th component is 1 and all the other components are 0.

Before introducing the main results，we first give two lemmas.In the following Lemma 1 and Lemma 2，L1，···，Ldare the non-trivial subspaces ofand dim（Li）=ri≤r，1≤i≤d. Here d，r are positive integers.

Lemma 1If q＞d，there exists an n-dimension vector α=（1，0，···，0，an-r+1，···，an）T∈such that

Proof Let

then|C1|=（q-1）qr.

The lemma is proved in two cases.

Case 1d=1.

The existence of α is proved by contradiction.If such a vector α doesn’t exist，C1⊆L1. From the fact that L1is a non-trivial subspace of，one can get

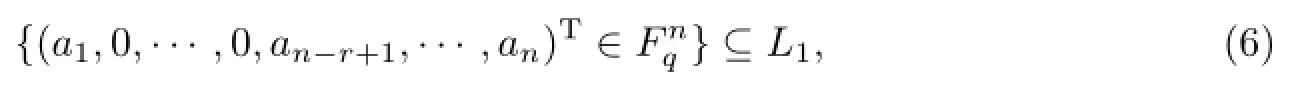
This is a contradiction to dim（L1）≤r.

Case 2d＞1.

Since

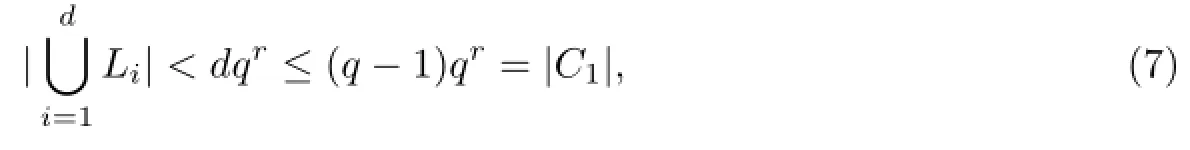
Therefore，from the proofs of Case 1 and Case 2，we can get the conclusion.

Lemma 2Let α1（i），···，αri（i）be a basis of the subspace Li，i=1，···，d.If q＞d，there exists n-dimension column vectors β1，···，βn-rsuch that for any i=1，···，d，β1，···，βn-r，α1（i），···，αri（i）are linearly independent.Moreover，β1，···，βn-rhave the form：

where In-ris the（n-r）×（n-r）identity matrix，Pr，n-ris some r×（n-r）matrix.

Proof The lemma is proved by induction.

From the Lemma 1，one can get a column vector β1satisfying Eq（8）.Assume β1，···，βjsatisfying Eq（8）have been chosen such that β1，···，βj，α1（i），···，αri（i）are linearly independent，where i=1，···，d，1≤j≤n-r-1.

Now，we prove that some βj+1of this form can be chosen such that β1，···，βj，βj+1，α1（i），···，αri（i）are linearly independent.

Let

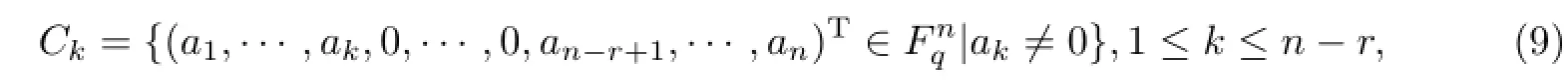
then|Ck|=（q-1）qk-1+r.

Two cases are discussed to complete the proof.

Case 1d=1.

The existence of βj+1is proved by contradiction.If such βj+1doesn’t exist，

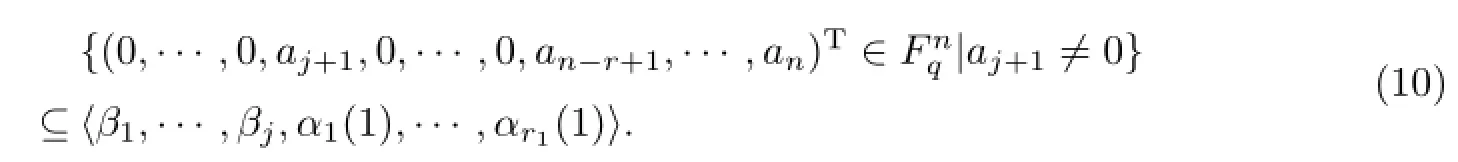
Together with｛β1，···，βj｝⊆〈β1，···，βj，α1（1），···，αr1（1）〉，one can get

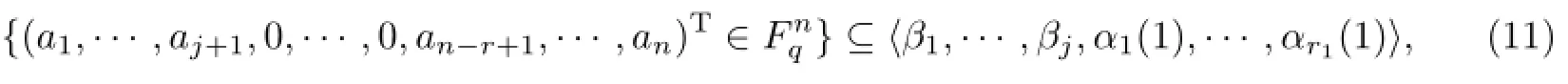
this is a contradiction to

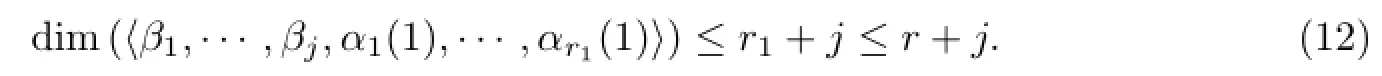
Case 2d＞1.

Since

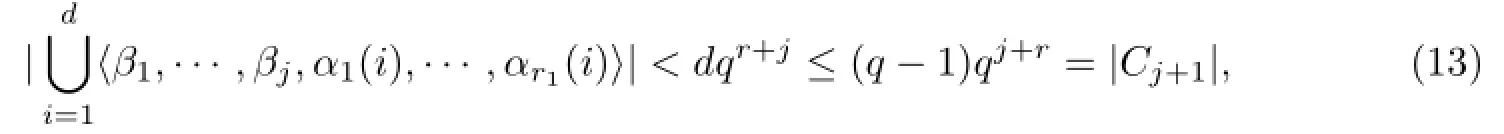
we can get

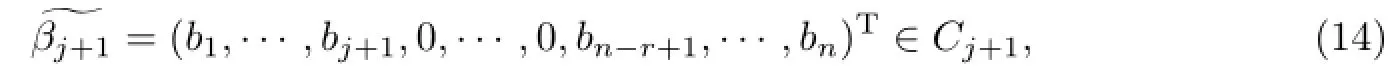
such that

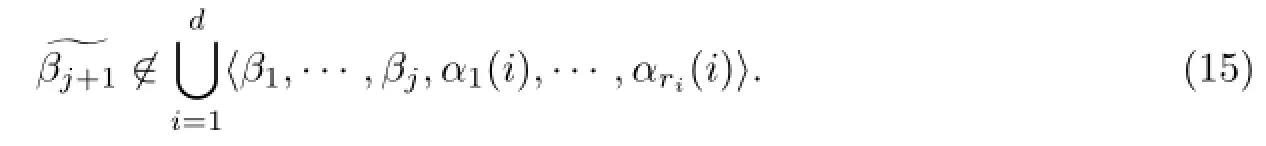
It is sufficient to take

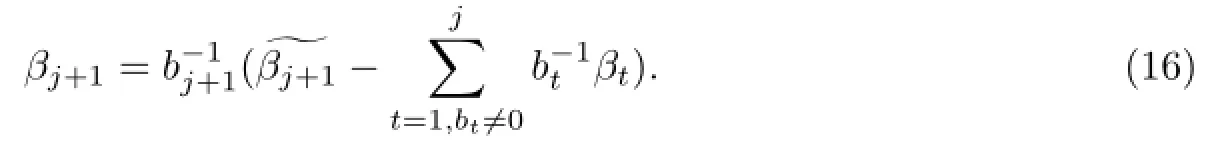
Therefore from the proofs of Case 1 and Case 2，we can get the conclusion.

Theorem 1If there exists an n-dimensional linear network code over Fq（q＞|A|）satisfying that for all the user nodes u∈U，dim（Vu）=n，and for all the wiretap sets of channels A∈A，dim（VA）≤r，the linear network code can be transformed into a linear admissible code

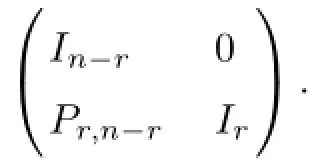
Let

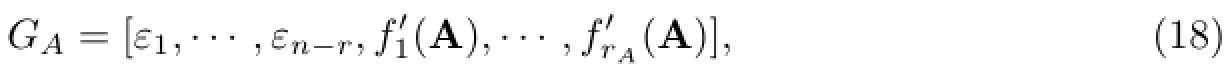
then the columns of

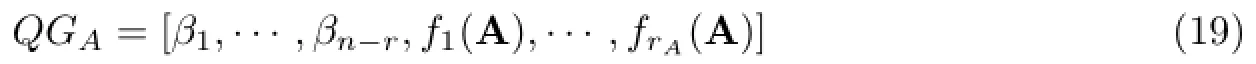
are linearly independent.Since rank（GA）=rank（QGA）=n-r+rA，then ε1，···，εn-r，are linearly independent for any A∈A.

Therefore，the given linear network code can be transformed into a secure network code by Q-1.

Since for all the user nodes u∈U，dim（Vu）=n and Q is a nonsingular matrix，we can get the image code is also decidable.Therefore，the given linear network code can be transformed into a linear admissible code by Q-1where Q has the form in Eq（17）.

Remark The transformation can also be regarded as its only being done at the source node and the operations at the intermediate nodes remain unchanged.In fact，for the image code，the transmitted information at the source node can be regarded as（m，k）Q-1while the global encoding kernelfor edge e∈E.

The sufficient condition in the Theorem 1 depends on a linear network code satisfying certain properties whose existence is hard to verify.Cai et al［2，7］get a more explicit sufficient condition which depends only on the graph G and the collection of wiretap channels A.

Let G∗=（V，E∗），where E∗⊆E，be a subgraph of satisfying

（i）For any u∈U，there are n disjoint paths in G∗from the source node s to the user node u.

（ii）For any A∈A，there are at most r disjoint paths in E∗from the source node s to the channels in A⊆E∗.

If q＞|U|，there exists an n-dimensional linear network code over Fqsatisfying that for all the user nodes u∈U，dim（Vu）=n，and for all the wiretap sets of channels A∈A，dim（VA）≤r. According to the sufficient condition over graph and Theorem 1，we can efficiently construct an n-dimensional linear admissible code.

3.2 Complexity Analysis

For the specific nonsingular matrix Q in Eq（17），it is evident that

The complexity of computing the matrix Q-1is O（1）.While for a general n×n nonsingular matrix，the complexity of calculating its inverse matrix is O（n3）.Moreover，since the matrix Q-1in Eq（20）is a special block lower triangular matrix，the complexity of computing Q-1feis O（r（n-r）），while for a general nonsingular n×n matrix，the complexity is O（n2）.From the complexity analysis，the specific construction of secure network coding is efficient.Its advantage is more evident when n becomes larger.

§4.Example

In this section，an example is given to illustrate the construction.Consider the CSWN shown in the Fig.1 with the set of user nodes U=｛u1，u2｝and the collection of sets of wiretap edges A=｛（y1，u1），（z，w），（y2，u2）｝.There are two disjoint paths from the source node s to theuser node u1and u2，respectively.However，there is only one path from s to any set of wiretap channels A.Thus，for a sufficiently large number q，an admissible code exists for n=2，|k|=1 and|m|=1.For this example，q=3 is enough.We can firstly construct the linear network coding by the global kernels

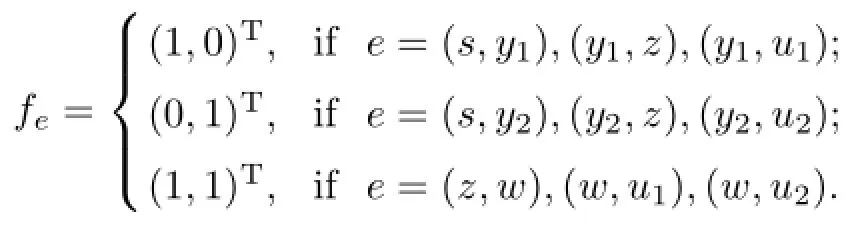
At the source node s，a message M and an independent random key K are generated according to the uniform distribution on the finite field F3.Denote the values taken by m and k，respectively.The source node s sends m+k and k to the nodes y1and y2，respectively.Then node y1sends m+k to the nodes z and u1and node y2sends k to the nodes z and u2.Upon receiving m+k and k，the node z sends m-k to the node w.Finally，the node w sends m-k to the two user nodes u1and u2.It is easy to check that such a code satisfies the decodable condition and the secure condition，which means it is an admissible code.

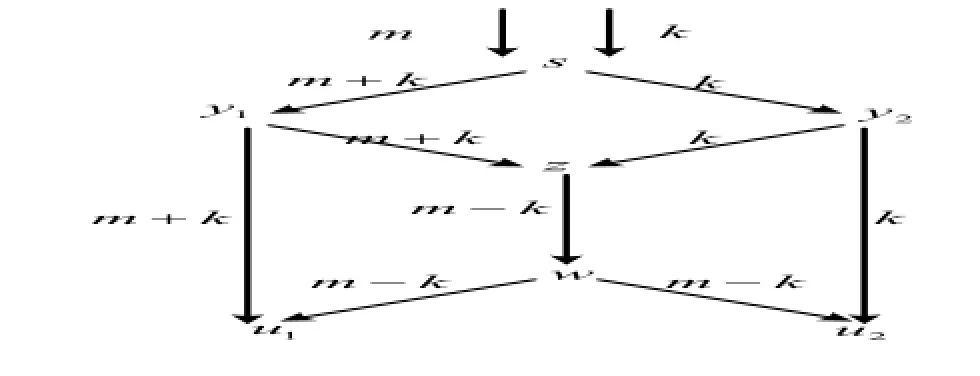
Fig.1　An Admissible Code for a Wiretap Network

§5.　Conclusions

We have found that the method of［2，7］implies an effective construction of secure network code over the CSWN Actually，it is proved that a linear network code can be transformed into a secure network code by a properly chosen nonsingular matrix Q-1which has the simple form in Eq（20）.From the complexity analysis，one can see the specific construction is more effective than the general construction method.Moreover，a secure network code can be constructed while keeping the random key unchanged at the source node since the transformation can also be regarded as to be done only at the source node and the operations at the intermediate nodes remain unchanged.It means that the linear network code can be transformed into a secure network code on the same network，while each non-source node only need to store one copy of the local encoding kernel with in a session.

［References］

［1］AHLSWEDE R，CAI Ning，LI S-Y R，et al.Network information flow［J］.IEEE Transactions on Information Theory，2000，46（4）：1204-1216.

［2］CAI Ning，YEUNG R W.Secure Network Coding［C］.Lausanne Switzerland：IEEE International Symposium on Information Theory，2002：323.

［3］FELDMAN J，MALKIN T，STEIN C，et al.On the Capacity of Secure Network Coding［C］.Monticello：Proc 42nd Annual Allerton Conference on Communication，2004.

［4］JAIN K.Security based on network topology against the wiretapping attack［J］.IEEE Wireless Communications，2004，11（1）：68-71.

［5］BHATTAD K，NARAYANAN K R.Weakly Secure Network Coding［C］.Rivapel Garda：Proc Winmee Rawnet and Netcod Workshops，2005：281-285.

［6］CAI Ning，YEUNG R W.A Security Condition for Multi-source Linear Network Coding［C］.Nice France：IEEE International Symposium on Information Theory，2007：561-565.

［7］CAI Ning，YEUNG R W.Secure network coding on a wiretap network［J］.IEEE Transactions on Information Theory，2011，57（1）：424-435.

［8］LI S-Y R，YEUNG R W，CAI Ning.Linear network coding［J］.IEEE Transactions on Information Theory，2003，49（2）：371-381.

［9］YEUNG R W，LI S-Y R，CAI Ning，et al.Network Coding Theory［M］.Foundations and Trends in Comunations and Information Theory：IEEE Information Theory Society，2005：11-25.

TP393Document code:A

date：2015-10-19

Supported by the National Natural Science Foundation of China（61201253）

Biographies：ZHANG Jing-li（1979-），female，native of Xuchang，Henan，a lecturer of Henan University of Technology，M.S.D.，engages in the theory of Coding；TANG Ping（corresponding author）（1979-），female，native of Nanyang，Henan，a lecturer of Henan University，M.S.D.，engages in the theory of coding.