A Remark on Global Existence，Uniqueness and Exponential Stability of Solutions for the 1D Navier-Stokes-Korteweg Equations

ZHANG Jian-lin，CAO Jie，SU Xing

（1.College of Information Science and Technology，Donghua University，Shanghai 201620，China；2.Department of Applied Mathematics，Zhongyuan University of Technology，Zhengzhou 450007，China）



A Remark on Global Existence，Uniqueness and Exponential Stability of Solutions for the 1D Navier-Stokes-Korteweg Equations

ZHANG Jian-lin1，2，CAO Jie1，SU Xing1

（1.College of Information Science and Technology，Donghua University，Shanghai 201620，China；2.Department of Applied Mathematics，Zhongyuan University of Technology，Zhengzhou 450007，China）

In this paper，we investigate non-isothermal one-dimensional model of capillary compressible fluids as derived by M Slemrod（1984）and J E Dunn and J Serrin（1985）.We establish the existence，uniqueness and exponential stability of global solutions in H2× H1×H1for the one-dimensional Navier-Stokes-Korteweg equations by a priori estimates，which implies the existence and exponential stability of the nonlinear C0-semigroups S（t）on H2×H1×H1.

Navier-Stokes equations；capillarity；Korteweg stress tensor

2000 MR Subject Classification:35Q35，35Q30，76N10

Article ID:1002—0462（2016）01—0027—12

Chin.Quart.J.of Math.

2016，31（1）：27—38

§1.　Introduction

In this paper，we study compressible fluids endowed with internal capillarity.We shall consider the following one-dimensional non-isothermal Navier-Stokes-Korteweg equations，which comes from Slemrod［19］and Dunn and Serrin［7］，

where u，v，σ，e and Q stand for the specific volume，velocity，stress，internal energy and heat flux，respectively.The stress σ is given by Korteweg’s theory of capillarity，i.e.，

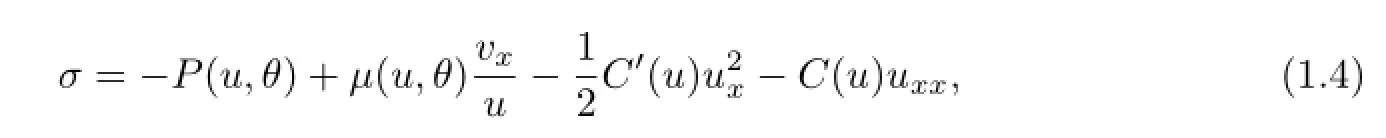
where C（u）is the capillarity coefficient，µ（u，θ）is the viscosity coefficient，P is the pressure，θ is the absolute temperature.We take the heat flux Q satisfying Fourier’s law

and let the capillarity C（u）=κ be a positive constant and hence the Korteweg tensor K= K（uxx）=-κuxxin order to simplify calculations.Thus，system（1.1）～（1.3）can be read as

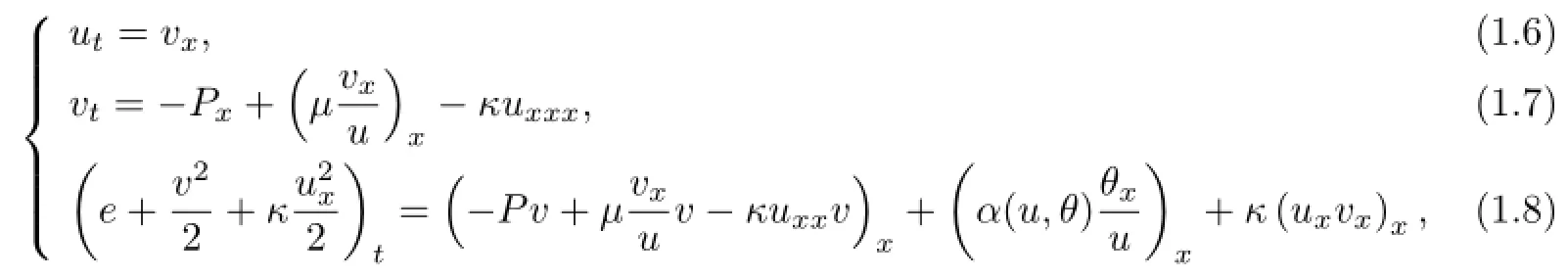
in the region｛0≤x≤1，t≥0｝under initial conditions

and the boundary conditions，namely，homogeneous Dirichlet conditions for the velocity

and the Neumann conditions for the specific volume

and the temperature

Now we mention some known results concerning the Korteweg type system.In the corresponding isothermal model，Danchin and Desjardins［6］studied the well-posedness of the model in spaces with critical regularity indices with respect to the scaling of the associated equations. In a functional setting as close as possible to the physical energy spaces，they proved the existence of solutions close to a stable equilibrium，and local in time existence for solutions when the pressure law may present spinodal regions.Bresch et al［1］considered a global existence of weak solutions in dimension 2 or 3 using the regularity of the density in a periodic domainΩ=Tn.Subsequently，they discussed the case of a smooth bounded domain depending on the choice of the diffusion term and on the boundary conditions，with a positive result in the caseΩ=（0，1）×Tn-1.Haspot［8］improved the existence of global weak solutions in dimension 2 for initial data in the energy space，close to a stable equilibrium and with specific choices on the capillary coefficients.Kotschote［13］proved existence and uniqueness of local strong solutions for this system by Dore-Venni theory，real interpolation，H∞-calculus and the contraction mapping principle.Tan，Wang and Xu［22］proved the global existence of a strong solution withthe small initial perturbation in R3.In the non-isothermal model，Kotschote［14］addressed the existence and uniqueness of strong solutions on bounded domain with compact boundaries by refined methods of maximal regularity.Recently，Kotschote［15］established global existence and uniqueness of strong solutions for initial data near equilibria and showed exponential stability of equilibria in the phase space.

The purpose of this paper is to establish the existence and exponential stability of time globally defined solutions to problem（1.6）～（1.12）.Compared with the case of compressible Navier-Stokes system［9-11］，the main difficulty we encounter here is the appearance of the higher order of the specific volume u which brings more difficulties to deduce the uniform a priori estimates for solutions of the initial boundary value problems.The main difficulty arises from the higher-order nonlinearities of θ and partial derivatives of u in system（1.6）～（1.8）.In order to overcome them，we make full use of corollaries 2.1 and 2.2 to reduce the higher order of θ and interpolation technique，and our main idea comes from Qin［16-18］.

In the present paper，our main novelties are as follows.（i）Slemrod［19］only considered the thermal conductivity α（u，θ）is positive constant，but here we consider the thermal conductivity α（u，θ）depends not only on the specific volume but also on the absolute temperature.（ii）In the proof of existence and exponential stability of global strong solutions，we make full use of the higher-order partial derivatives of the specific volume.Moreover，our method and initial value space are different with those in Kotschote［14］.Kotschote［14］only proved the existence and uniqueness of strong solutions when the initial data（u0，v0，θ0）∈W3-2/p，p×W2-2/p，p× W2-2/p，p（n+2＜p＜+∞，n≥1）.

In what follows，spaces Lp，1≤p≤+∞ denote the usual Lebesgue spaces on（0，1）and‖·‖Bdenotes the norm in the space B，‖·‖：=‖·‖L2.The mean valueLetter C will denote the general constant，but may be different from time to time and letter C1will denote the universal positive constant depending on the norms of initial datum（u0，v0，θ0）inu0（x）andθ0（x），but being independent of t，respectively.

We organize our present paper as follows.In Section 2，we will state our main result.In Section 3，we will complete the proof of our theorem.

§2.Main Result

In this section，we will state our main theorem.Firstly，we give some assumptions.The internal energy e and the pressure P are coupled by the standard thermodynamical relation

Assume that e，P，σ and α are smooth sufficiently on 0＜u＜+∞and 0≤θ＜+∞and there exist the exponents q and r satisfying one of the following relations

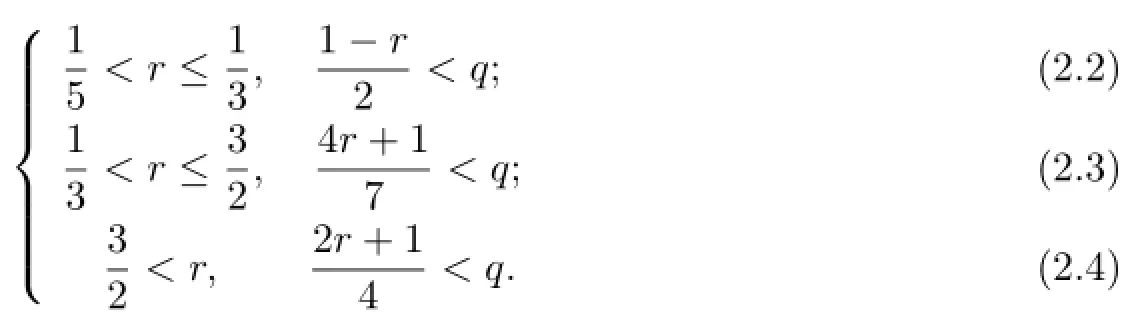
In order to describe clearly growth conditions with respect to the temperature，we require that there be positive exponents r and positive constants ν，p1，p2，α0and that for any＞0，there be positive constantssuch that forw∈R and θ≥0，the following growth conditions hold

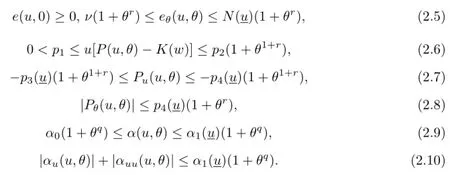
In addition，we suppose that the viscosityµ（u，θ）is independent of θ，uniformly positive and bounded，i.e.，

Now we define the space as

which become the metric space when equipped with the metrics induced from the usual norms. Here Hi=Wi，2（i=1，2）are the usual Sobolev spaces.

We are in a position to state our main result.

Theorem 1Assume that e，P，σ and α are C2functions on u∈（0，+∞）and θ∈［0，+∞）and the assumptions（2.1）～（2.11）hold.Then the problem（1.6）～（1.12）admits the unique generalized global solution（u（x，t），v（x，t），θ（x，t））in，which defines a nonlinear C0-semigroup S（t）on.Moreover，for any（u0，v0，θ0）∈，there exists a constant γ1= γ1（C1）＞0 such that for any fixed γ∈（0，γ1］and for any t∈（0，+∞），the following estimate holds

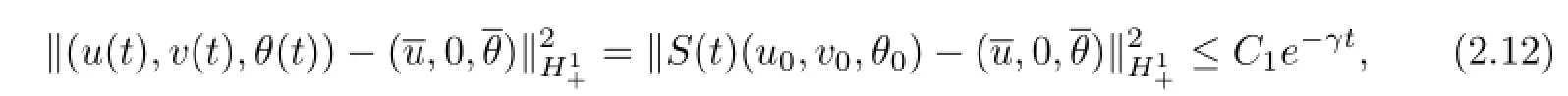
that is，the semigroup S（t）is exponentially stable on.Hereand the constantsatisfiesis the unique solution to the corresponding stationary problem to（1.6）～（1.12）.

Remark 1Here we consider the non-isothermal case and our model is the more generalized than those in［20-21］.

Remark 2We have not obtained the similar results within this work，so we may study this case by the other technique in the future.

§3.Proof of Theorem

In this section，we shall show the global existence，uniqueness，asymptotic behavior and exponential stability to the problem（1.6）～（1.12）.That is，we shall complete the proof of Theorem.First，we give some a priori estimates.

Noting that（1.8）is the parabolic equation，we can obtain the positivity of θ（x，t）.Using the similar method as in lemmas 2.1.1～2.1.2 of Qin［16］，we can establish the following estimates with a minimal modification，for any（x，t）∈［0，1］×［0，+∞），

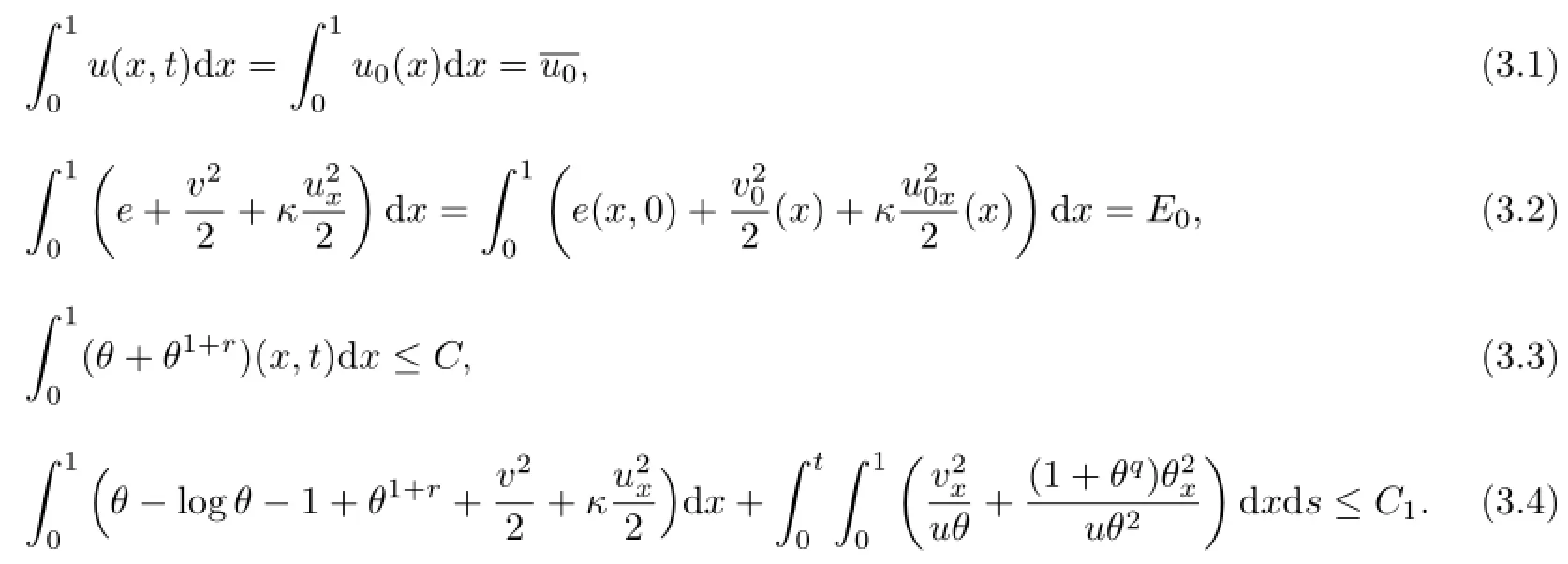
Replacing p by P-K and going along the line of argumentation in the proof of Lemma 2.1.3 in Qin［16］，we can see that，for any t∈［0，+∞），there exists one point x1=x1（t）∈［0，1］such that the solution u（x，t）to problem（1.6）～（1.12）can be expressed as

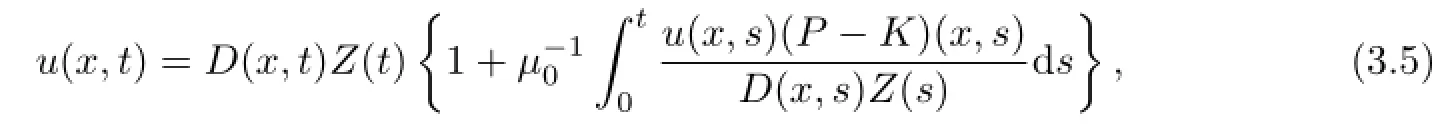
where

By virtue of the similar method of Lemma 2.1.5 in Qin［16］，we can deduce from（3.5）the upper and positive lower bounds of solution u（x，t），that is，for any（x，t）∈［0，1］×［0，+∞），

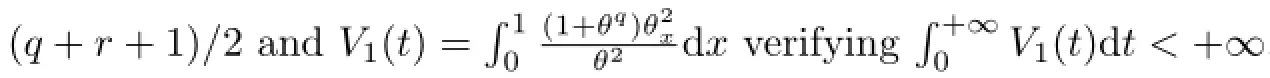
which，combined with（3.4）and the weighted H¨older inequality，leads to

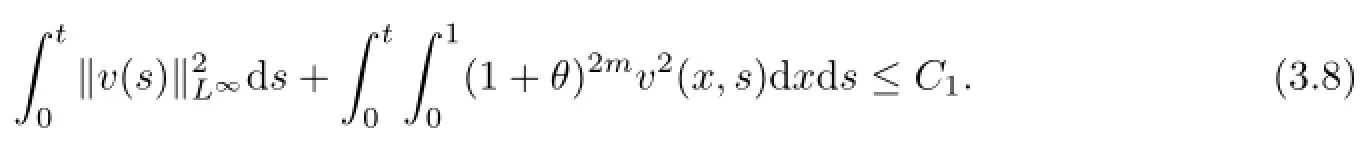
Using an integration by parts，we can obtain

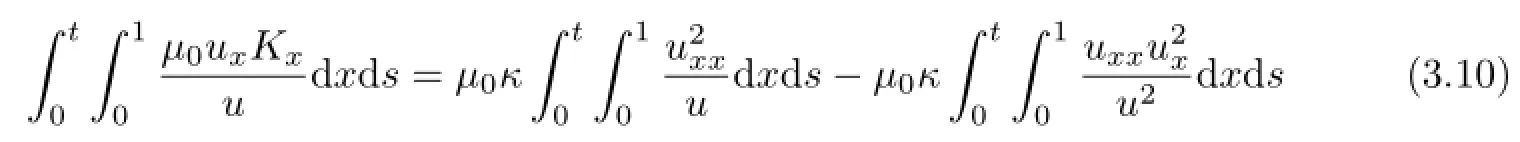
and

Using（3.4），the Sobolev embedding theorem and the Cauchy inequality，we have

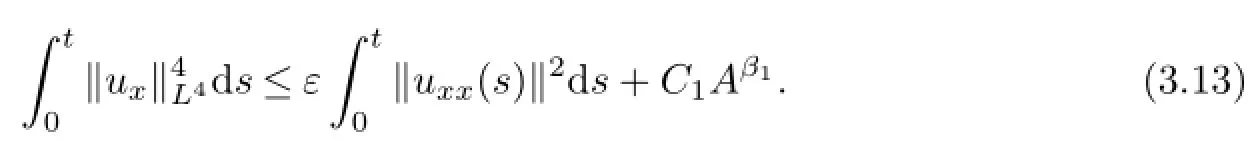
Using the Cauchy inequality，（3.10）～（3.13）and（2.7），we can deduce from（3.7），

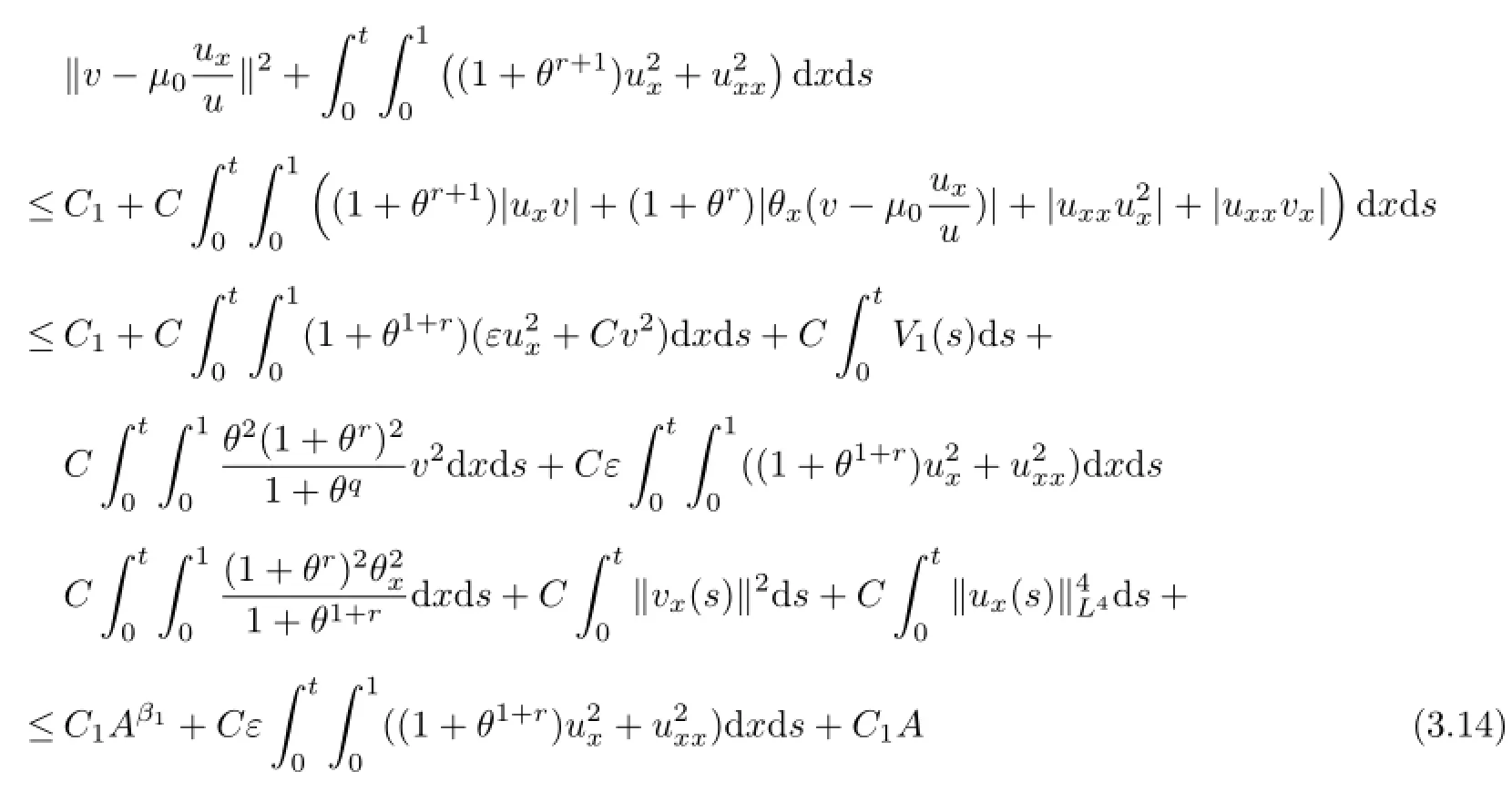
with β1=max（r+1-q，0）.Taking ε＞0 small enough，we obtain

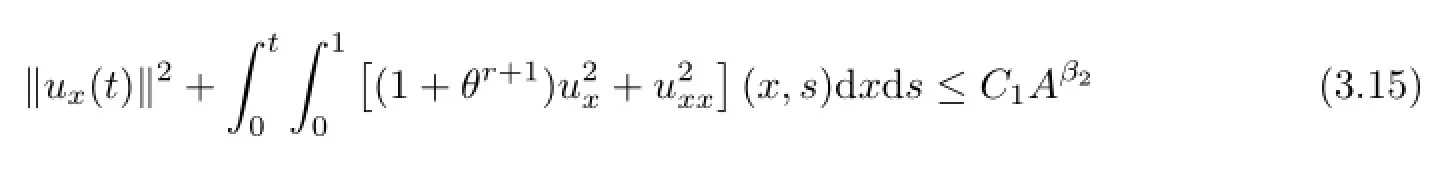
with β2=max（1，β1）.

Using（3.15）and（3.7），by the Sobolev embedding theorem，we can easily obtain the following estimates

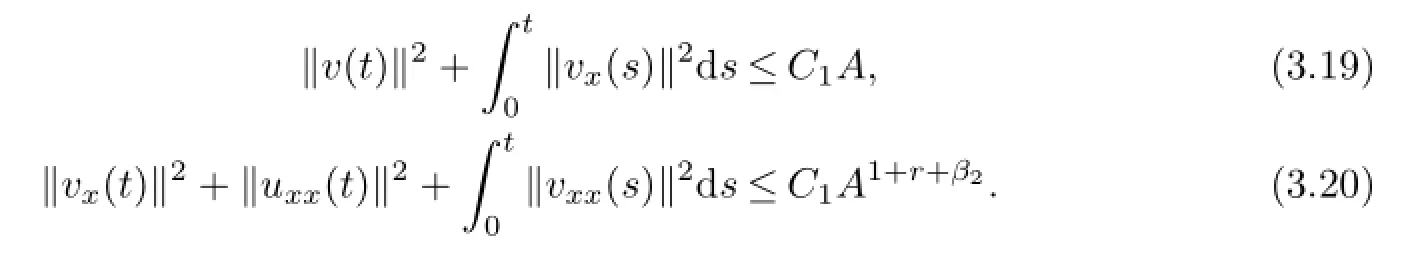
Using the method of Lemma 2.1.8 in Qin［16］，we can deduce from the H¨older inequality that

which，combined with（3.19）～（3.20），we can derive from the Gagliardo-Nirenberg inequality that

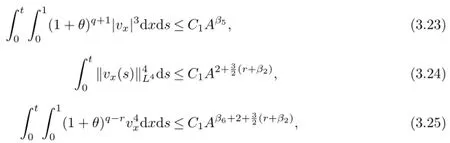
Using the similar method as the proofs of lemmas 2.1.9～2.1.10 in Qin［16］，we can establish the following estimates with a minimal modification，we omit the detailed proof

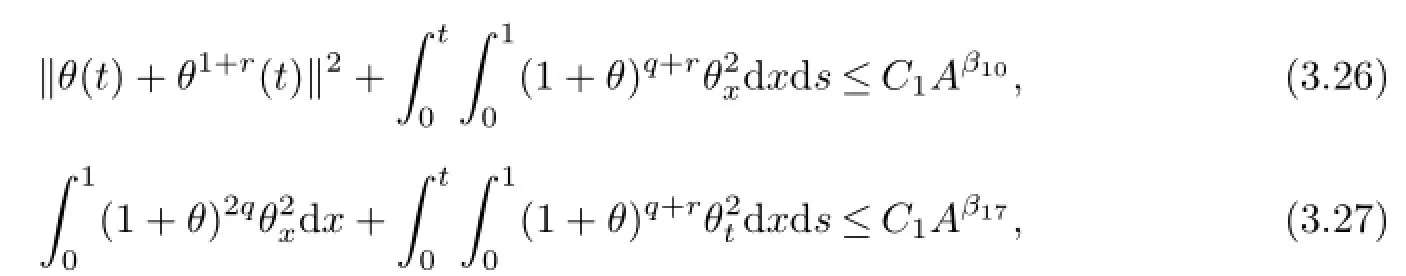
where

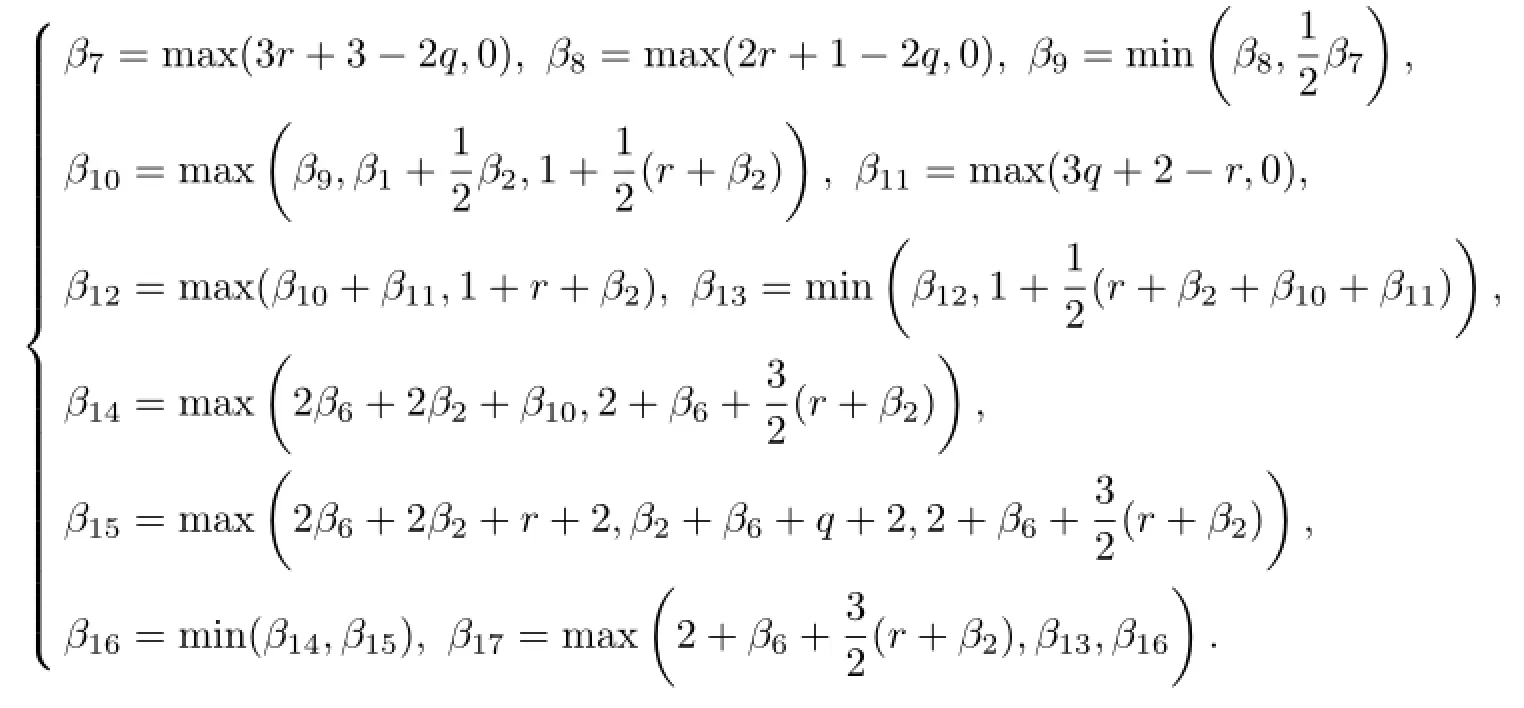
Similarly to the proof of Lemma 2.1.11 in Qin［16］，using the Sobolev embedding theorem，（3.27）and the Young inequality，we can obtain

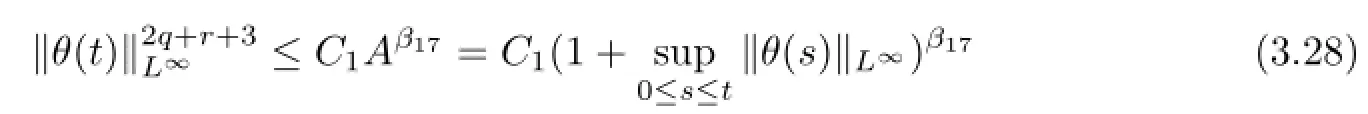
and

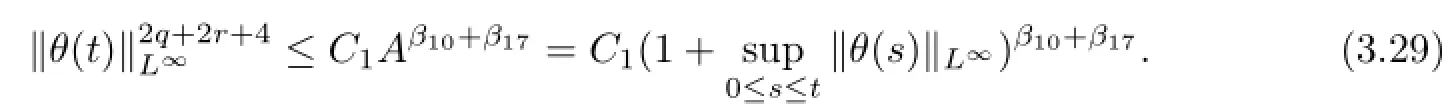
After a lengthy calculation，we can derive from the assumptions（2.2）～（2.4）that β10+β17＜2q+2r+4 or β17＜2q+r+3.Therefore，using the Young inequality，we deduce from（3.28）or（3.29）that

which，furthermore，combined with（3.4），（3.6），（3.8），（3.12），（3.15）～（3.16），（3.20），（3.26）～（3.27）and（3.30），we obtain the desired estimate

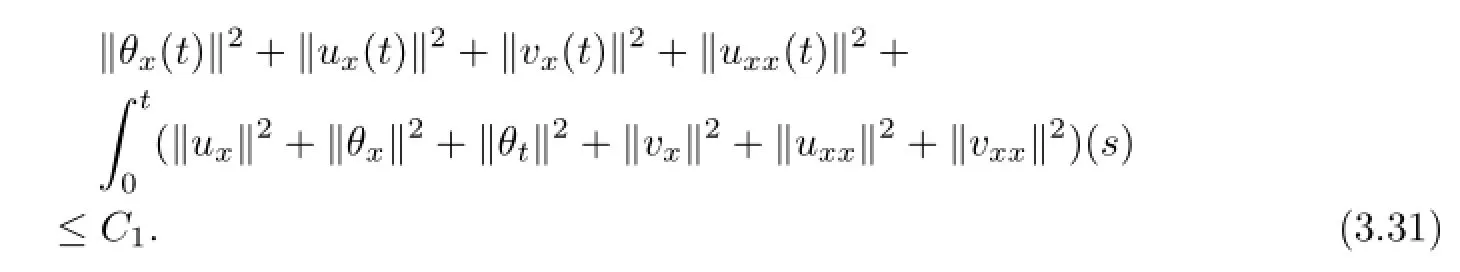
We deduce from（1.8）and（3.31）that

Based on the above estimates，we can now show the asymptotic behavior of solutions to the problem（1.6）～（1.12）in.Similarly to the proof of Lemma 2.1.14 in Qin［16］，we have，as t→+∞，

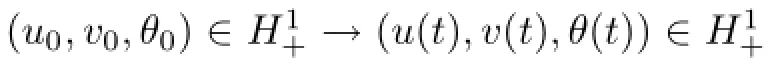
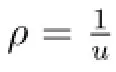
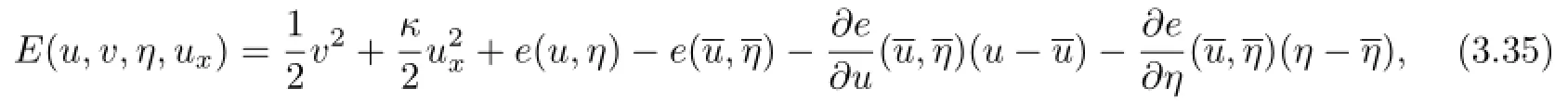
Similarly to the proof of Lemma 2.4 in Qin［17］，we can obtain that，for the unique generalized global solution（u（t），v（t），θ（t））to the problem（1.6）～（1.12），the following estimate holds

It follows from equations（1.6）～（1.8）that（ρ，v，η）satisfies

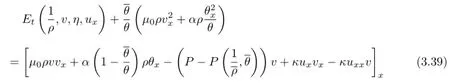
and

Multiplying（3.39）～（3.40）by eγt，βeγt，respectively and then adding the results up，we can get

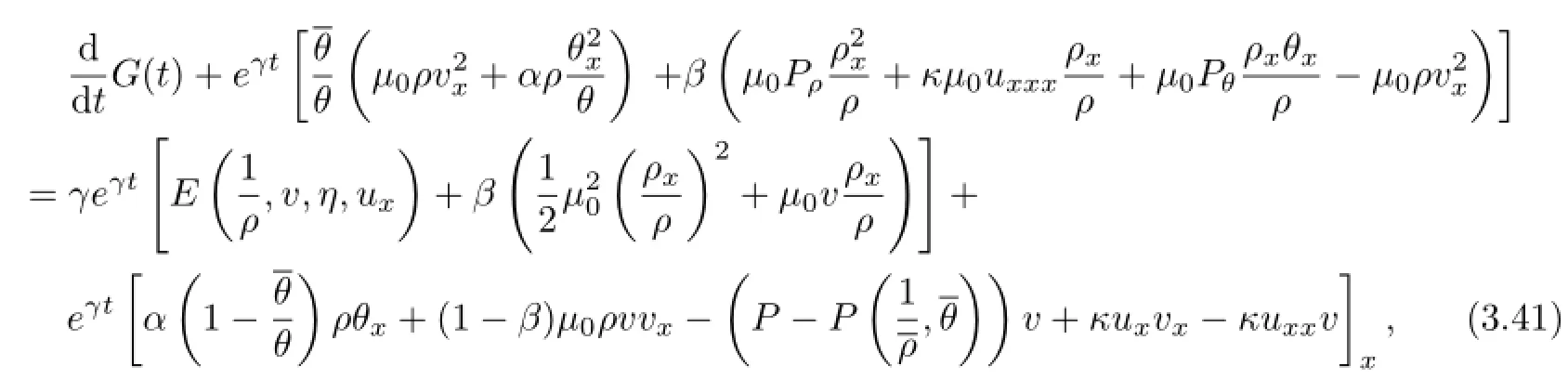
Multiplying（1.7）by vxxin L2［0，1］，we have

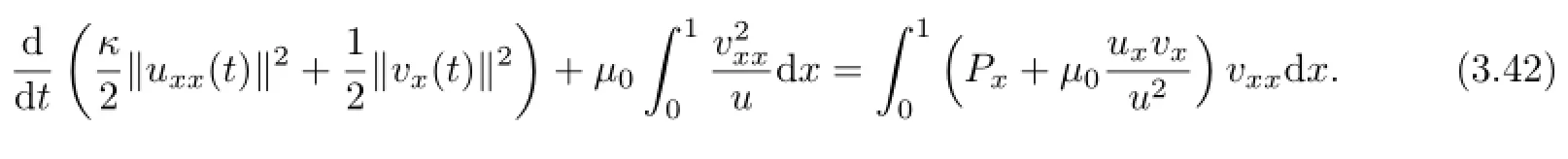
Integrating（3.41）over［0，1］with respect to x，multiplying（3.42）by eγt，adding the results up and then using the Cauchy inequality and the Poincar`e inequality，we deduce from（3.31）～（3.32），（3.34）and（3.36）that for small β＞0 and for any γ＞0，

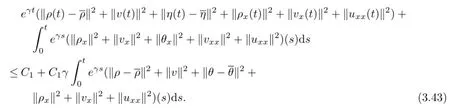
Similarly to the proof of Lemma 2.5 in Qin［17］，we know from（3.43）that there exists a constant γ′1=γ′1（C1）＞0 such that for any fixed γ∈（0，γ′1］，the generalized global solution（u（t），v（t），θ（t））to the problem（1.6）～（1.12）satisfies for any t∈（0，+∞），

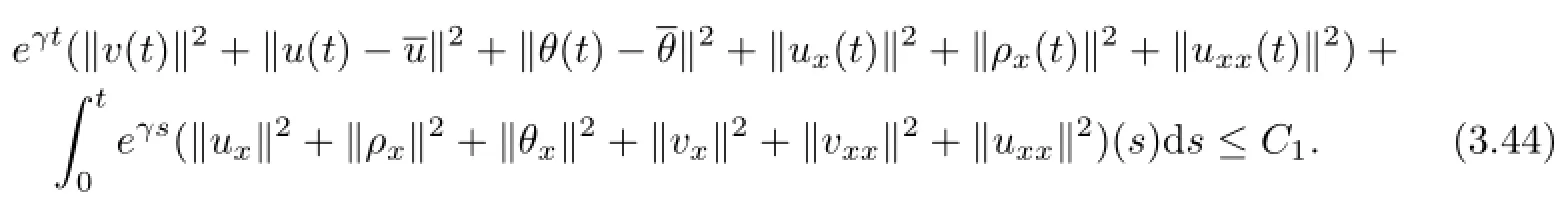
Noting the fact that similarly to the proof of Lemma 2.6 in Qin［17］，we can deduce that there exists a positive constant γ1=γ1（C1）≤γ′1such that for any fixed γ∈（0，γ1］，the generalized global solution（u（t），v（t），θ（t））into the problem（1.6）～（1.12）satisfies for any t∈（0，+∞），

which，combined with（3.44），yields（2.12）.Thus we complete the proof of Theorem.

［References］

［1］BRESCH D，DESJARDINS B，LIN C K.On some compressible fluid models：Korteweg，lubrication and shallow water systems［J］.Comm.Partial Differential Equations，2003，28（3-4）：843-868.

［2］BONA J L，SACHS R L.Global existence of smooth solutions and stability of solitary waves for a generalised Boussinesq equation［J］.Commun Math Phys，1988，118（1）：15-29.

［3］CHARVE F，HASPOT B.Existence of global strong solution and vanishing capillarity-viscosity limit in one dimension for the korteweg system［J］.SIAM J Math Anal，2013，45（2）：469-494.

［4］CHEN Zheng-zheng.Asymptotic stability of strong rarefaction waves for the compressible fluid models of Korteweg type［J］.J Math Anal Appl，2012，394：438-448.

［5］CHEN Zheng-zheng，XIAO Qing-hua.Nonlinear stability of viscous contact wave for the one-dimensional compressible fluid models of Korteweg type［J］.Mathematical Methods in the Applied Sciences，2013，36：2265-2279.

［6］DANCHIN R，DESJARDINS B.Existence of solutions for compressible fluid models of Korteweg type［J］. Ann Inst H Poincar´e Anal Non Lin´eaire，2001，18（1）：97-133.

［7］DUNN J E，SERRIN J.On the thermomechanics of interstitial working［J］.Arch Rat Mech Anal，1985，88（2）：95-133.

［8］HASPOT B.Existence of global weak solution for compressible fluid models of Korteweg type［J］.J Math Fluid Mech，2011，13：223-249.

［9］HUANG Fei-min，LI Jing，MATSUMURA A.Asymptotic stability of combination of viscous contact wave with rarefaction waves for one-dimenional compressible Navier-Stokes system［J］.Arch Rat Mech Anal，2010，197：89-116.

［10］HUANG Fei-min，MATSUMURA A，XIN Zhou-ping.Stability of contact discontinuities for the 1-D compressible Navier-Stokes equations［J］.Arch Rat Mech Anal，2006，179：55-77.

［11］HONG Hakho.Global stability of viscous contact wave for 1-D compressible Navier-Stokes equations［J］.J Differ Equ，2012，252：3482-3505.

［12］KATO T.Quasi-linear Equations of Evolution，with Applications to Partial Differential Equations［M］. Berlin：Springer，1975.

［13］KOTSCHOTE M.Strong solutions for a compressible fluid model of Korteweg type［J］.Ann I H Poincar´e-AN，2008，25：679-696.

［14］KOTSCHOTE M.Dynamics of compressible non-isothermal fluids of non-Newtonian Korteweg type［J］. SIAM J Math Anal，2012，44（1）：74-101.

［15］KOTSCHOTE M.Existence and time-asymptotics of global strong solutions to dynamic Korteweg models［J］. Indiana Univ Math J，2014，63：21-51.

［16］QIN Yu-ming.Nonlinear Parabolic-Hyperbolic Coupled Systems and Their Attractors［M］.Basel-Boston-Berlin：Birkhauser Verlag AG，2008.

［17］QIN Yu-ming.Exponential stability for a nonlinear one dimensional heat-conductive viscous real gas［J］.J Math Anal Appl，2002，272：507-535.

［18］QIN Yu-ming.Universal attractor in H4for the nonlinear onedimensional compressible Navier-Stokes equations［J］.J Differ Equ，2004，207：21-72.

［19］SLEMROD M.Dynamic phase transitions in a Van Der Waals Fluid［J］.J Differ Equ，1984，52：1-23.

［20］TSYGANOV E.Global existence and asymptotic convergence of weak solutions for the one-dimensional Navier-Stokes equations with capillarity and nonmonotonic pressure［J］.J Differ Equ，2008，245：3936-3955.

［21］TAN Zhong，GUO Rong-cong.Global existence of weak solutions for the Navier-Stokes equations with capillarity on the half-line［J］.Nonlinear Differ Equ Appl，2011，18：459-481.

［22］TAN Zhong，WANG Hua-qiao，XU Jian-kai.Global existence and optimal L2decay rate for the strong solutions to the compressible fluid models of Korteweg type［J］.J Math Anal Appl，2012，390：181-187.

O175.29Document code:A

date：2015-12-20

Supported by the National Natural Science Foundation of China（11271066）；Supported by the Shanghai Education Commission（13ZZ048）

Biographies：ZHANG Jian-lin（1977-），male，native of Luoyang，Henan，an associate professor of Zhongyuan University of Technology and a Ph.D.candidate of Donghua University，engages in nonlinear evolution equations and infinite-dimensional dynamical systems.