Vertex Algebra Sheaf Structure on Torus

SUN Yuan-yuan

（Department of Public，Guangzhou Huaxia Technical College，Guangzhou 510900，China）



Vertex Algebra Sheaf Structure on Torus

SUN Yuan-yuan

（Department of Public，Guangzhou Huaxia Technical College，Guangzhou 510900，China）

In this paper，we first give a 1-1 corresponds between torus C/Λ and cubic curve C inAs complex manifold，they are isomorphic，therefore we can treat C/Λ as a variety and construction a vertex algebra sheaf on it.

torus；vertex algebra；sheaf

2000 MR Subject Classification:14A99，17B69

Article ID:1002—0462（2016）01—0044—07

§1.　Introduction

Chin.Quart.J.of Math.

2016，31（1）：44—50

Vertex algebras have been studied by mathematicians for more than a decade，but still very little is known about the general structure of vertex algebra.H Li［10］B Feigin and E Frenkel［6］，I Frenkel and Y Zhu［11］give some examples respectively.Vadim Schechtman［2］proved that we can define certain sheaves of vertex algebras on smooth manifolds in 1999.As an example，we construct a vertex algebra sheaf structure on torus.

To prepare for our work，we begin in section 2 by reviewing the basic concepts of torus and Heisenberg vertex algebra.In section 3，we construct a vertex algebra sheaf on torus.

§2.Torus and Heisenberg Vertex Algebra

2.1 Torus

We will define torus as C/Λ，which Λ≡｛mω1+nω2|m，n∈Z｝≡（（ω1，ω2））is a lattice.（ω1，ω2∈C and linear independent）.It is not difficult to prove that C/Λ isomorphic to C⊂， which is a cubic curve.

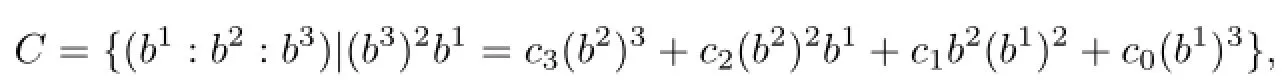
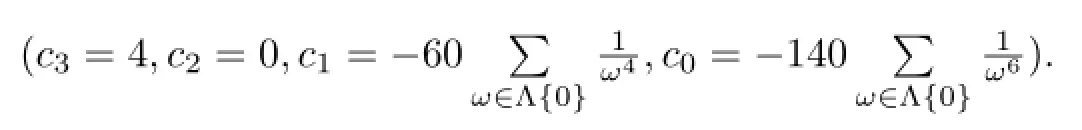
C is a variety and C is also a scheme.Projective subschema inalways are ProjC［x0，x1，x2］ /I，where I is a homogeneous ideal.So we have C=ProjC［b1，b2，b3］（f），f=（b3）2b1-c3（b2）3-c2（b2）2b1-c1b2（b1）2-c0（b1）3，it means C/Λ～=C=ProjC［b1，b2，b3］/（f）.Now，we can define our vertex algebra sheaf on C/Λ.

2.2 Heisenberg Vertex Algebra

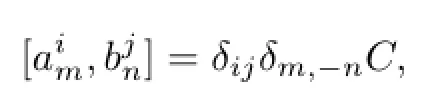
all other brackets being zero.

As an H3-module，V3=〈1〉，subject to the relations：

Let us define the structure of a conformal vertex algebra on V3.

•（Vacuum Vector）1；

•（Translation Operator）L-11=0，［L-1，an］=-nan-1，［L-1，bn］=-（n-1）bn-1；

•（Vertex Operators）

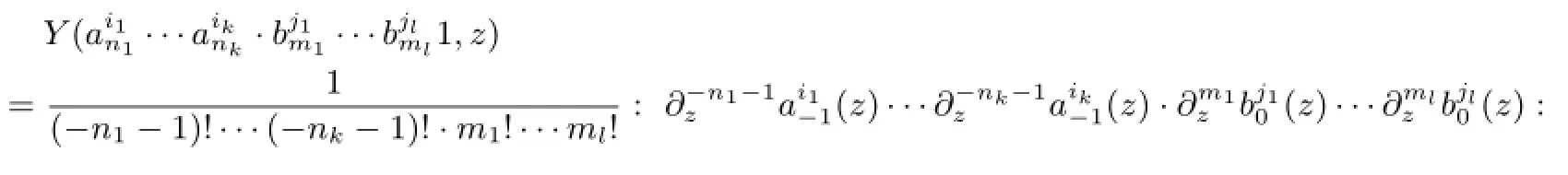
•（Locality）

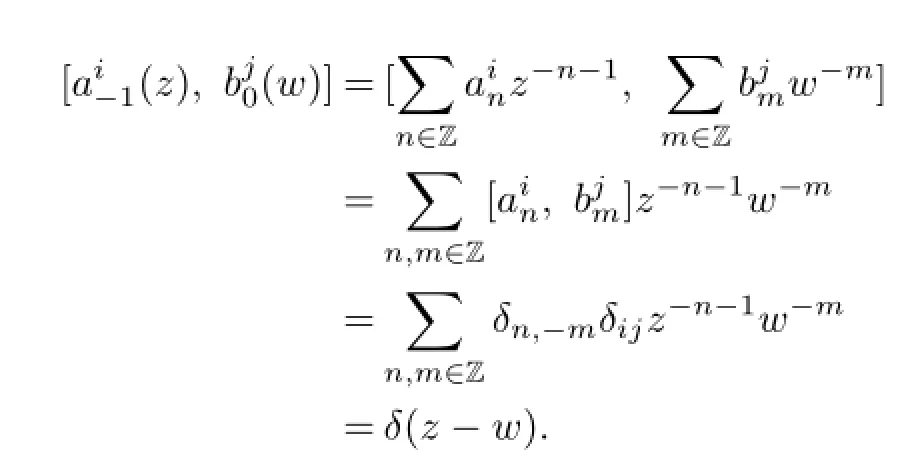
•（Conformal Structure）Conformal vector

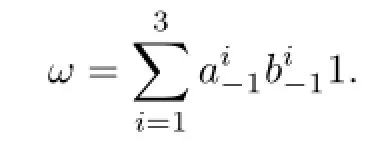
Virasoro field

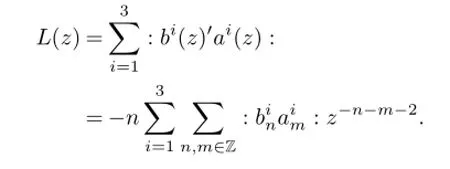
In other words，vertex algebra V3is generated by the even fields bi（z），aj（z）of conformal weights 0 and 1 respectively，subject to the relations above.

§3.　Define Sheaf of Vertex Algebra on Torus

We know C=ProjC［b1，b2，b3］/（f）and the equation of cubic curve C is f=（b3）2b1-c3（b2）3-c2（b2）2b1-c1b2（b1）2-c0（b1）3.Let A3=C［b1，b2，b3］/（f），then we haveProj（A3）.So we get V3is A3-module.

Proposition 1Define vertex algebra sheaf on torus.

Proof

Step 1In the Zariski topology，open sets on C/Λ are Distinguished open subsets.We choose three open subsets as the base

The three forming topological base

And，

Step 2We define structure of vertex algebras on the Distinguished open subsets，i.e.，define V3；bi，i=1，2，3 are vertex algebras.

We are going to introduce a structure of a conformal vertex algebra on the spaceLet us define the map

We have

•（Vertex Operators）Because V3is conformal vertex algebra，we just need check

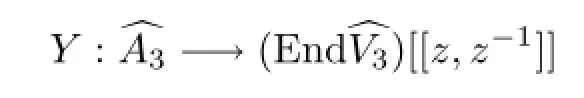
is well defined.

Choose a formal power serieswe prove thatis an element in

First，we have

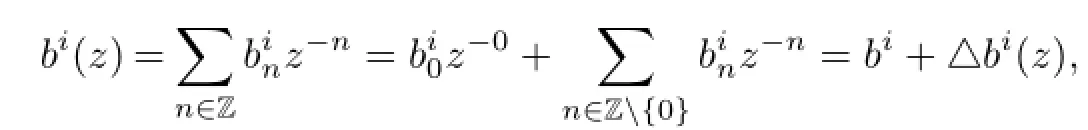
Let us define by the Taylor formula

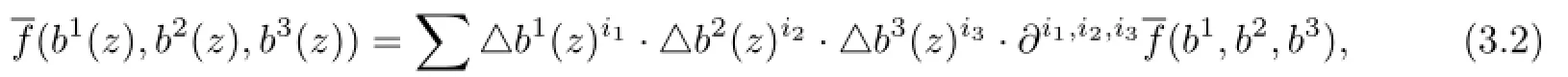
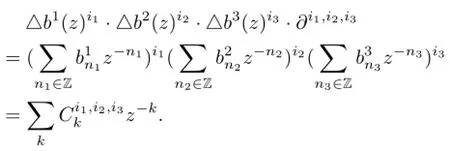
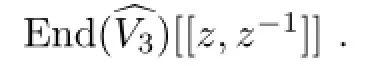
On the other hand，

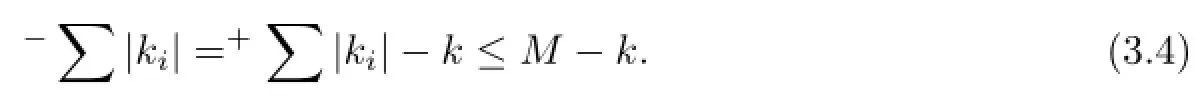
There exists only a finite number of tuples（k1，···，kI）satisfying（3.3）and（3.4）.Therefore，are well defined endomorphisms of

So，

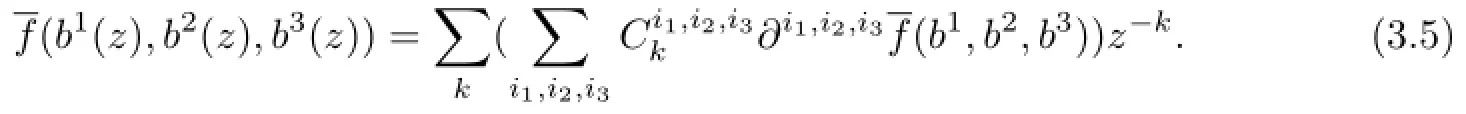
All ki≠0.Let I+（I-）be the number of positive（negative）ki.We haveM-k，hencetherefore，I≤2M-k. Therefore，when（3.5）action on the element v，only a finite number of terms in the sun over（i1，i2，i3）survives.Therefore，（3.5）is a well defined element of End

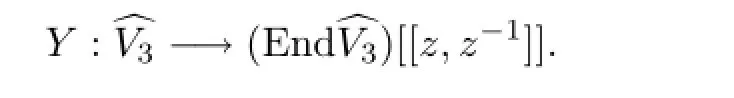
•（Locality）

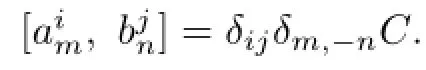
•（Conformal Structure）We can get it from the map（3.1）.

Next，we construct a structure of a conformal vertex algebra on the space V3；b1.

Since V3；b1=A3；b1⊗A3V3，therefore，the vacuum vector，translation operator，conformal structure of V3；b1are similar to

•（Vertex Operators）

（b1（z））-1=（b0+b1（z）+b1z-1+···）-1

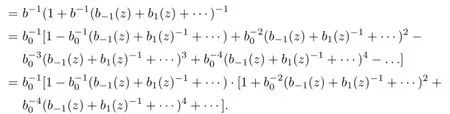
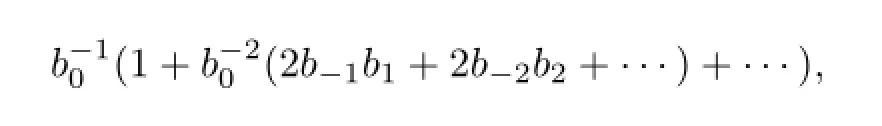
The coefficient of z0istherefore the coefficient at each power of z is an infinite sum，but as an operator acting on V3；b1，it is well defined since only finite number of terms act nontrivially.

We know

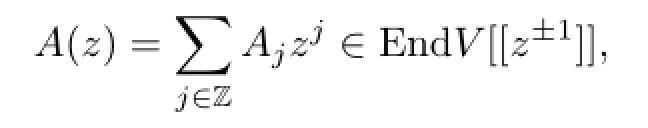
For any v∈V and large enough j，we have Aj·v=0.In other words A（z）·v∈V（（z））.

By the above（3.6），we can give the general field

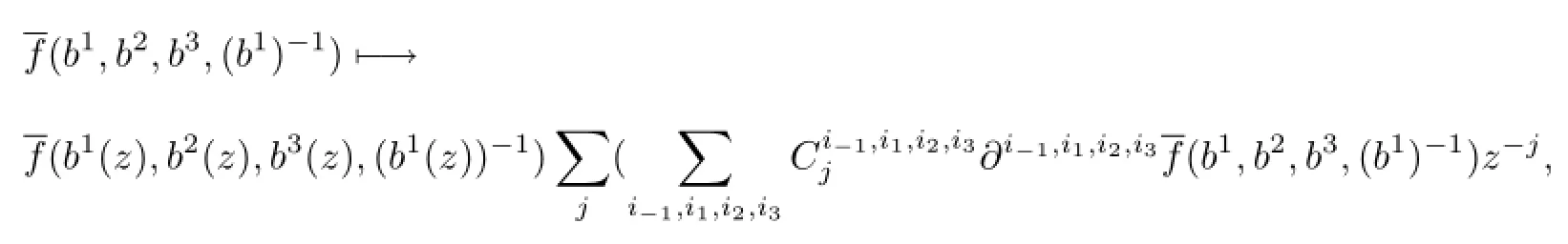
•（Locality）We have［bn，bm］=0，then we get

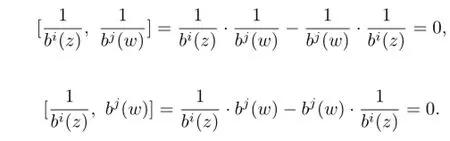
Therefore，we completed the structure of a conformal vertex algebra on the space V3；b1.Then， sectionis also a conformal vertex algebra，this Proposition provides a structure of a conformal vertex algebra on sectionand section Γ

Step 3Section which corresponding to any open set are all vertex algebra.For any open set U⊂X，we define

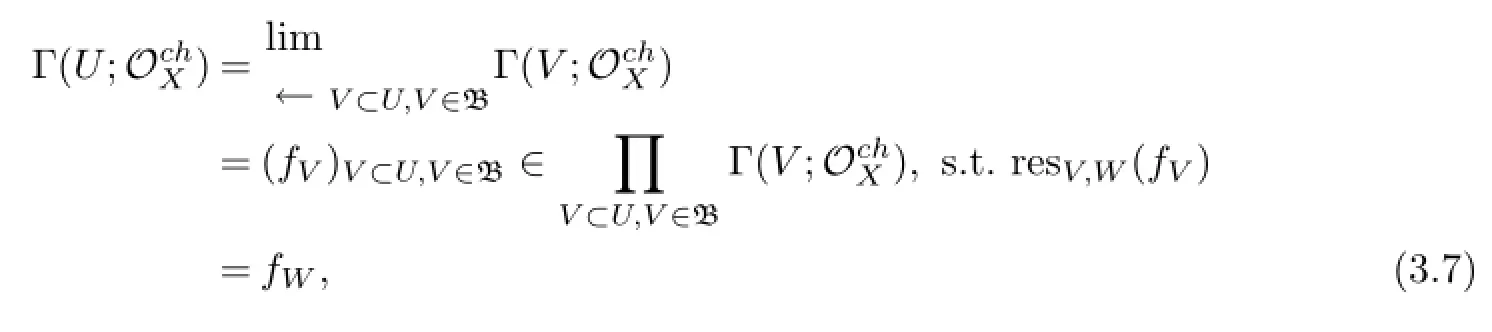
which W ⊂V⊂U and V，W ∈B.The element of Γcan be regard as limit of the element which belongs to Γand their vacuum vector，translation operator，vertex operator are the same.Then we get Γis also a vertex algebra.

Step 4Define the restriction map.∀U，V⊂X and U⊂V，we have known that bothandare vertex algebras.Therefore，the restriction map is a morphism of vertex algebras.By［9］andare satisfy the morphism of vertex algebras.

Obviously，we have

（2）For all open set，U，ρUUis identity map；

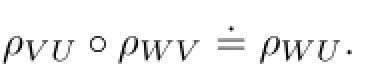
Then，we construct a presheaf.

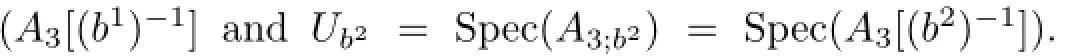
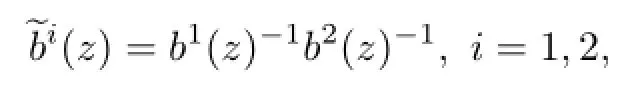
then we glue the two open subsets together.

Now，we complete the structure of vertex algebra sheafon torus C/Λ.

［References］

［1］GEHRING F W，HALMOS P R，MORRE C C.Lectures on Riemann Surfaces［M］.New York：Springer-Verlag，1981.

［2］MALIKOV F，SCHECHTMAN V，VAINTROB A.Chiral de Rham complex［J］.Comm Math Phys，1999：204：439-473.

［3］MEURMAN A，PRIMC M.Vertex operator algebras and representations of affine Lie algebras［J］.Acta Applicandae Math，1996，44：207-215.

［4］DAVID EISENBUD，JOE HARRIS.The Geometry of Schemes［M］.New York：Springer-Verlag，2000.

［5］ROBIN HARTSHORNE.Algebraic Geometry［M］.New York：Springer Verlag，1999.

［6］CHANDRASEKHARAN K.Elliptic Functions［M］.New York：Springer-Verlag，1985.

［7］DONG C，LEPOWSKY J.Generalized Vertex Algebras and Relative Vertex Operators［M］.Boston：Birkh¨auser，1993.

［8］EDWARD FRENKEL，DARID Ben-Zvi.Vertex Algebras and Algebraic Curves［M］.New York：American Mathematical Society，2001.

［9］LI Hai-sheng.Local systems of vertex operators，vertex superalgebras and modules［J］.Pure Applied Algebra，1996，109：143-195.

［10］FRENKEL I，ZHU Yong-chang.Vertex operator algebras associated to representations of affine and Virasoro algebras［J］.Duke Math，1992，66（1）：123-168.

［11］XU Xiao-ping.Introduction to Vertex Operator Super algebras and Their Modules［M］.Dordrecht/Boston/ London：Kluwer Academic，1998.

［12］DONG Cong-ying.Twisted modules for vertex algebras associated with even lattices［J］.Algebra，1994，165：91-112.

O187.1，O412.3Document code:A

date：2015-09-10

Supported by the National Natural Science Foundation of China（11475178，11571119）

Biography：SUN Yuan-yuan（1983-），female，native of Jiaozuo，Henan，a lecturer of Guangzhou Huaxia Technical College，M.S.D.，engages in mathematical physics.