Bohr Inequality for Multiple Operators

LIAN Tie-yan，TANG Wei

（1.Faculty of Light Industry and Energy，Shaanxi University of Science and Technology，Xi’an 710021，China；2.College of Electrical and Information Engineering，Shaanxi University of Science and Technology，Xi’an 710021，China）



Bohr Inequality for Multiple Operators

LIAN Tie-yan1，TANG Wei2

（1.Faculty of Light Industry and Energy，Shaanxi University of Science and Technology，Xi’an 710021，China；2.College of Electrical and Information Engineering，Shaanxi University of Science and Technology，Xi’an 710021，China）

An absolute value equation is established for linear combinations of two operators. When the parameters take special values，the parallelogram law of operator type is given.In addition，the operator equation in literature［3］and its equivalent deformation are obtained. Based on the equivalent deformation of the operator equation and using the properties of conjugate number as well as the operator，an absolute value identity of multiple operators is given by means of mathematical induction.As Corollaries，Bohr inequalities are extended to multiple operators and some related inequalities are reduced to，such as inequalities in［2］and［3］.

Bohr inequality；absolute value operator；adjoint operator；mathematical induction

2000 MR Subject Classification:47A63

Article ID:1002—0462（2016）01—0039—05

Chin.Quart.J.of Math.

2016，31（1）：39—43

§1.　Introduction

Let B（H）be the algebra of all bounded linear operators on a complex separable Hilbert space H.As usual，I is the identity operator，C is the set of complex numbers and R is the set of real numbers.Denote by¯α the conjugate of α and by|A|the absolute value operator of，where A∗is the adjoint operator of A.Note that|A|=0 if and only if A=0.We write A≥0 if A is a positive operator，i.e.，（Ax，x）≥0 for all x∈H.A≥B if A and B are self-adjoint operators and A-B≥0.

There exist a great number of results on the absolute value operator.The classical Bohr inequality［1］for scalars asserts that

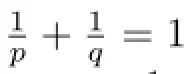
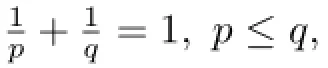
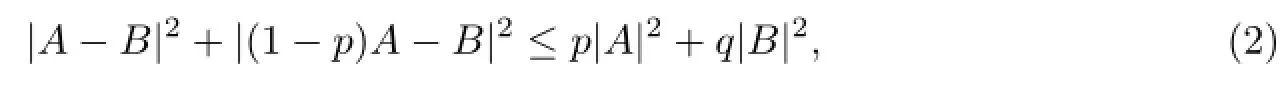
especially，as a Corollary of（2），［2］has the following result.

In［3］，F Zhang presented an operator equation from which（2）follows immediately and the condition p≤q was removed.We will give a more extensive operator equation，from which many equations including F zhang’s can be produced in this paper.Bohr inequalities are studied in many papers，we can refer to［4-8］.

§2.　Preliminaries

Theorem 1Let A，B∈B（H），α，β，µ，ν，∈C，p，q≥0.If|α|2+|µ|2=p，|β|2+|ν|2= q，Then

Proof It is easy to compute that

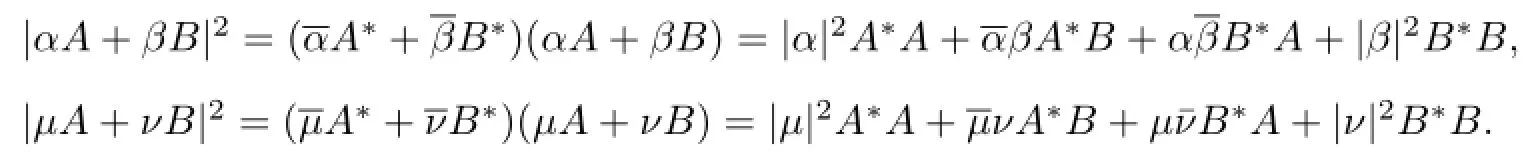
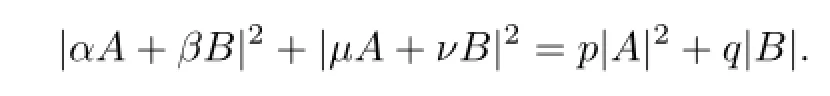
This completes the proof.

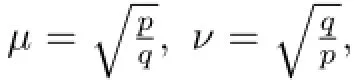
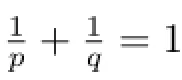
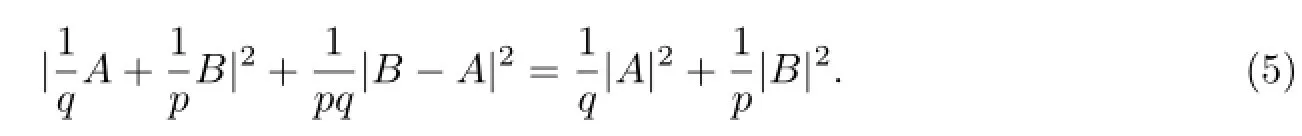
Corollary 2Let A，B∈B（H），θ∈R，then

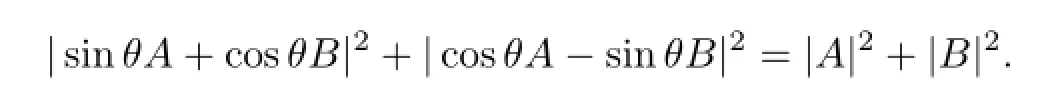
Proof If θ∈R，trigonometric identity similar to sin2θ+cos2θ=1 still holds.Therefore，we only need to let α=sinθ，β=cosθ，µ=cosθ，ν=-sinθ in Theorem 1.

Corollary 3Let A，B∈B（H）.If 0≤α≤1，then

Corollary 4［4］Let A，B∈B（H）.If 0≤α≤1，then

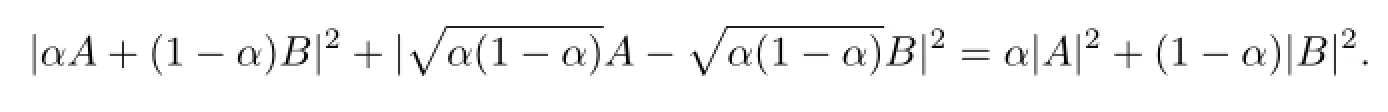
Equation（5）can be extended to the following result for a number of operators.

Theorem 2Let A1，A2，···，Ak∈B（H）.If t1+t2+···+tk=1，ti≥0，then

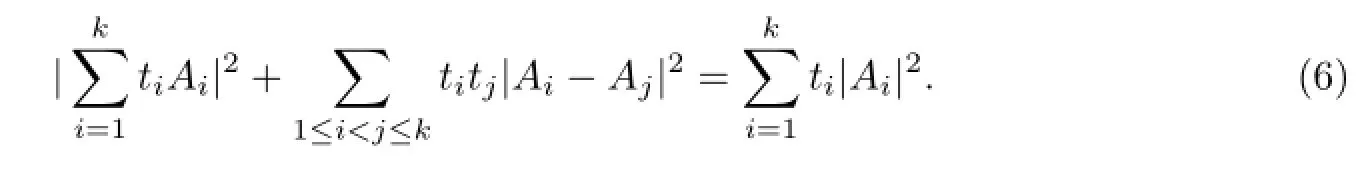
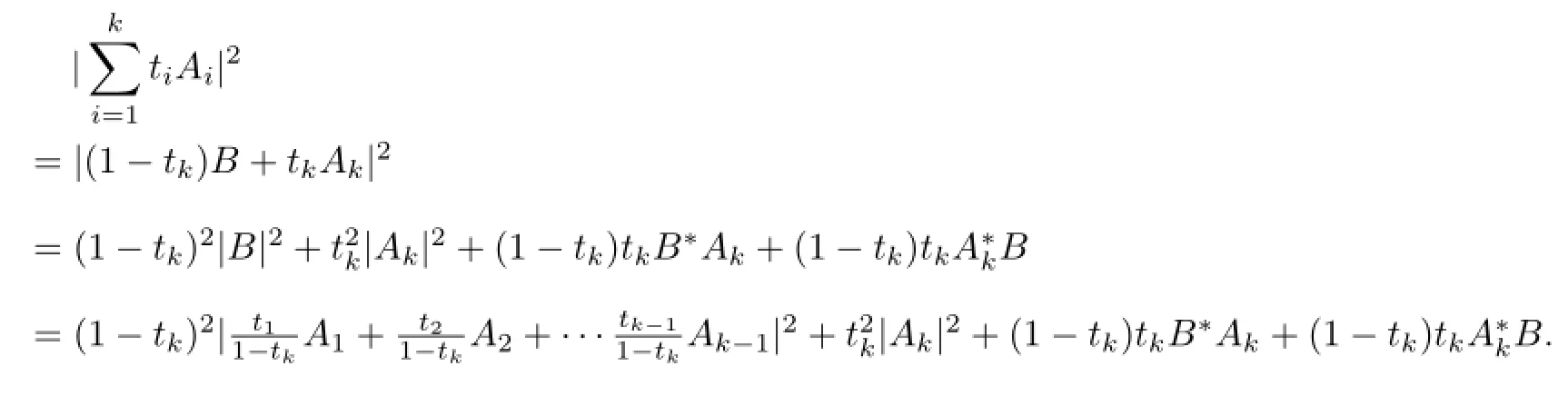
According to the hypothesis，

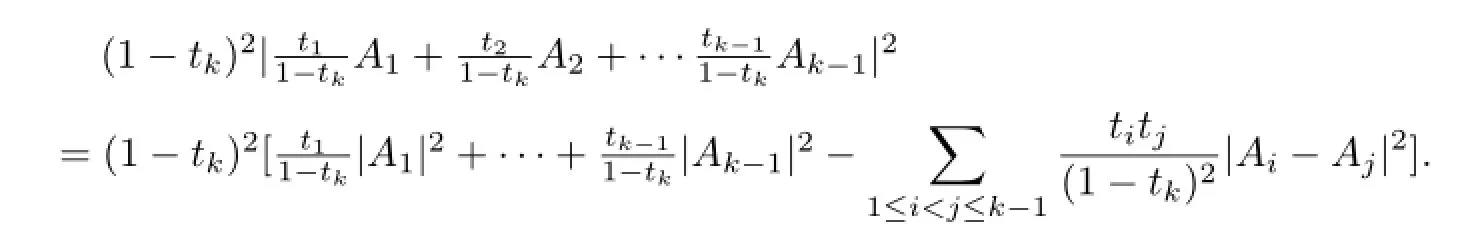
However，

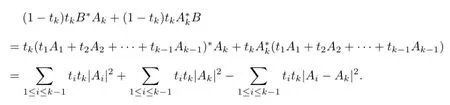
Thus

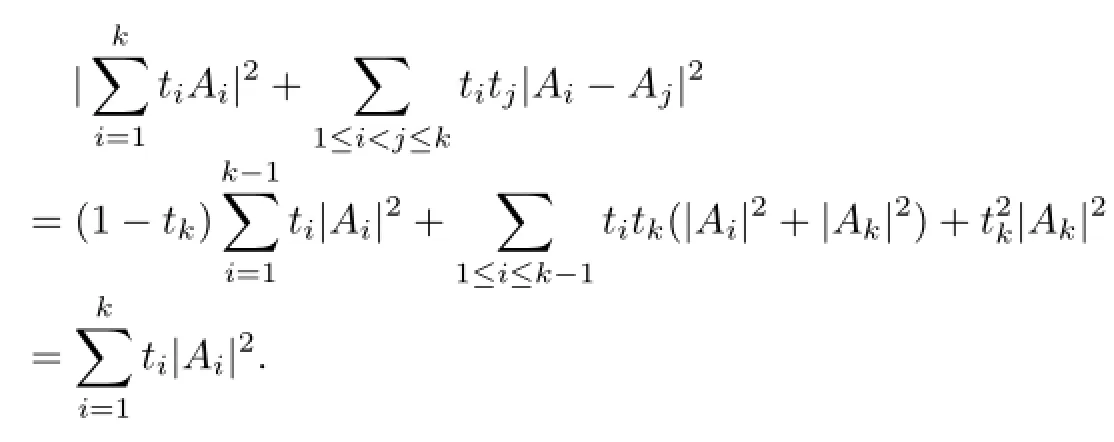
By the principle of mathematical induction，the result holds.

Using Theorem 2，Theorem 7 of［3］below holds naturally.

Corollary 5Let A1，A2，···，Ak∈B（H）.If t1+t2+···+tk=1，ti＞0，then

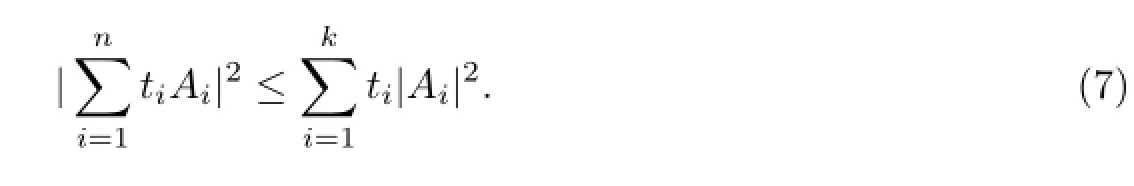
And the equality holds if and only if A1=A2=···=Ak.

Corollary 6Let A1，A2，···，An∈B（H）.Then

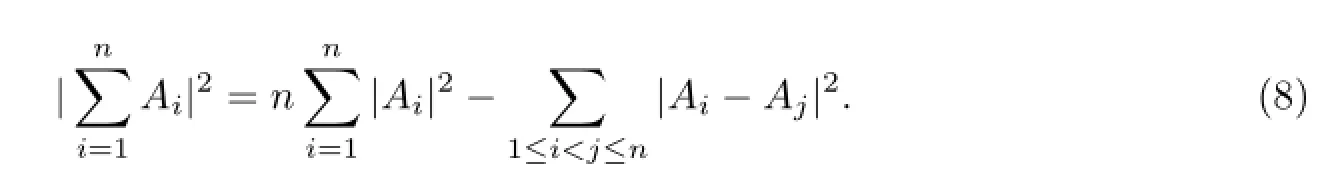
In［5］，W.S.Cheung mentioned the following generalization of Adamovic’s result［9］to B（H）.But the proof of the theorem did not notice that the operator is not exchangeable.In this section we will give a correct proof.

Theorem 3Let A1，A2，···，An∈B（H）.Then

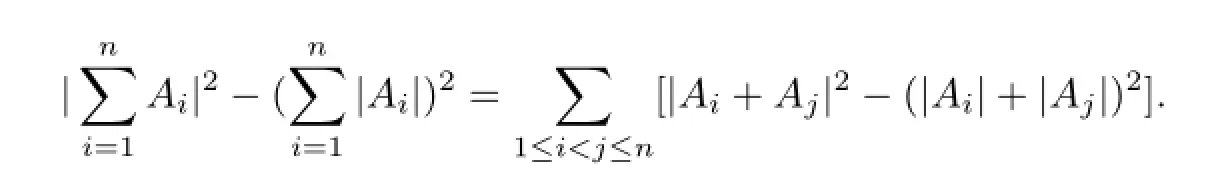
Proof We use the induction on n.Clearly the result holds for n=2.Suppose now thatthe result holds for n=k，then

Corollary 7Let A1，A2，···，An∈B（H）.Then

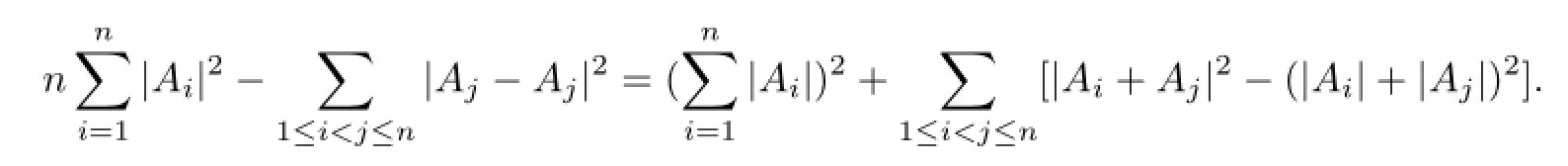
［References］

［1］MITRINOVIC D S.Analytic Inequalities［M］.New York：Springer，1970.

［2］HIRZALLAH O.Non-commutative operator Bohr inequality［J］.Journal of Mathematical Analysis and Applications，2003，282（2）：578-583.

［3］ZHANG Fu-zhen.On the Bohr inequality of operators［J］.Journal of Mathematical Analysis and Applications，2007，333（2）：1264-1271.

［4］SHOSHANA A，JOSIPA B，JOSIPA P.A new proof of an inequality of Bohr for Hilbert space［J］.Linear Algebra and its Applications.2009，430（4）：1432-1435.

［5］WING-Sum C，JOSIP P´cari´c.Bohr’s inequalities for Hilbert space operators［J］.Journal of Mathematical Analysis and Applications，2006，323（1）：403-412.

［6］WANG Jian-fei，LIU Tai-shun.Bohr’s inequality on the unit ball［J］.Chinese Quarterly Journal of Mathematics，2007，22（2）：159-165.

［7］AIZENBERG L.Multidimensional analogues of Bohr’s theorem on power series［J］.Proceedings of The American Mathematical Society，2000，128（4）：1147-1155.

［8］AIZENBERG L，AYTUNA A，DJAKOV P.Generalization of a theorem of Bohr for bases in spaces of holomorphic functions of several complex variables［J］.Journal of Mathematical Analysis and Applications，2001，258（2）：429-4474.

［9］ADAMOVI´C D D.Quelques remarques relatives aux g´en´eralisations des in´egalit´es de Hlawka et de Hornich［J］.Mat Vesnik，1964，1（16）：241-242.

O177.1Document code:A

date：2014-09-24

Supported by the Key Scientific and Technological Innovation Team Project in Shaanxi Province（2014KCT-15）

Biography：LIAN Tie-yan（1978-），female，native of Weinan，Shaanxi，a lecturer of Shaanxi University of Science and Technology，M.S.D.，engages in operator theory.