利用跟踪微分器计算天线角速度
李庆华
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
利用跟踪微分器计算天线角速度
李庆华
(中国电子科技集团公司第五十四研究所,河北 石家庄050081)
伺服系统中天线角速度是一个很重要的指标。在周期性角度采样的条件下,采用跟踪微分器(TrackingDifferentiator,以下简称TD)可以以简单的算法得到实时、平稳、准确的角速度。
伺服系统;角速度;跟踪微分器
引言
伺服系统中天线角速度是一个很重要的指标。除非是动载体需要增加陀螺环,安装速度传感器是一个很不经济的设计。目前仍然经常采用掐秒表的方法来测量角速度,这种方法耗费时间长,误差大,人工测量结果无法融入系统。在周期性角度采样的条件下,通过角度变化得到角速度是一个直观、可靠的途径。由于角度采样的结果是一个离散量,不能直接用来计算产生其微分量——速度。
采用跟踪微分器(TrackingDifferentiator,以下简称TD)[1]可以很好地解决以上问题,得到的角速度实时、平稳、准确。
1 跟踪微分器
跟踪微分器TD是中科院数学所韩京清研究员提出的对连续信号进行跟踪并对其微分信号进行估计的数值算法,由于其良好的跟踪性能和抗干扰能力,已成功应用于控制器设计和信号处理中。跟踪微分器具有多种形式,得到普遍应用的是二阶离散跟踪微分器,算法如下:
(1)
式中
v(k)为输入信号;
x1(k)为信号的跟踪输出;
x2(k)为信号微分的输出;
r为速度因子,可调参数;
h0为滤波因子,可调参数;
h为积分步长;
函数fhan(x1(k)-v(k),x2(k),r,h)由下列关系决定:
(2)
记
则式(2)可以改写成
(3)
2 利用TD计算角速度
伺服系统中天线轴角是最基本的特征量,因此系统需要实时采集角度传感器的信息,以获得天线轴角。在高性能的伺服系统中,实时性要求较高,轴角采集和闭环运算需要按照设定的采样时间Ts进行。这种情况下可以方便地运用TD计算天线的角速度。下面简单介绍利用TD计算角速度的方法。
2.1变量定义
除了最终结果—速度量Speed外,还需要定义一个全局变量即角度估计值AnglePr。变量数据类型与采样角度Angle相同(当然速度量必须为有符号数),为便于计算最好定义成float型。
2.2函数声明
需要三个函数:符号函数sign(t),char型或int型;符号函数的变异fsg(x,d),int型;最速控制综合函数fhan(x1,x2,r,h0),float型;r,h,h0可以是常量,也可以是局部变量,其余所有参变量数据类型为float型,局部变量。前两个函数是为后一个函数服务的。
2.3函数定义
(1) sign(t)函数
如果t<0,返回值-1;
如果t=0,返回值0;
如果t>0,返回值1。
(2) fsg(x,d)函数
返回值=(sign(x+d)-sign(x-d))/2。
(3) fhan(x1,x2,r,h0)函数
定义局部变量d,a0,y,a1,a;
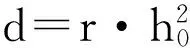
a0=h0·d;
y=x1+a0;
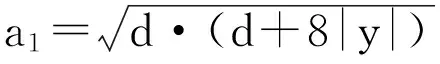
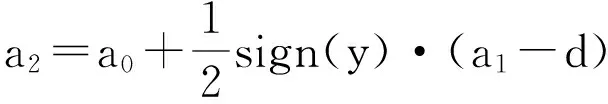
a=(a0+y)·fsg(y,d)+a2·(1-fsg(y,d));
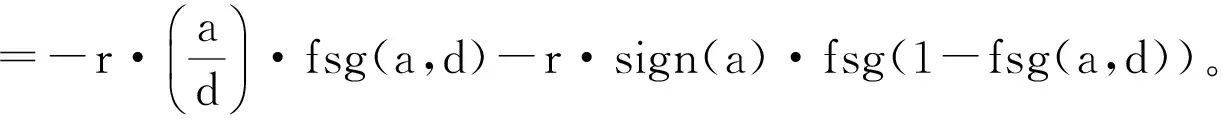
2.4初始化
初始化时先调用角度采集函数得到当前角度Angle,并将AnglePr赋值为Angle;Speed赋值为0。
2.5函数调用
函数调用过程中所有参变量要有确定的值。其中x1=AnglePr-Angle,x2=Speed,r取值大于系统可能的加速度即可,例如100,h=Ts,h0=(1~5)h。
每次角度采样后,随即调用相关函数进行如下计算:
中间变量temp0=AnglePr-Angle;
中间变量ahan=fhan(temp0,Speed,r,h0);
AnglePr=AnglePr+h·Speed;
Speed=Speed+h·ahan。
采用中间变量除了书写方便外,更重要的是在旋转天线系统中有角度过零问题和周期问题,即360°= 0°。在已知的系统中,相邻两次采样的角度差不会大于180°,对temp0进行处理以得到-180°~180°以内的角度。如果是其他系统不存在上述问题,则可以直接计算。
以上方法在以C8051F040为核心的伺服控制系统中成功计算速度量并在多个项目中应用。引导天线位置闭环等速转动,将计算的速度量显示在终端上,可以看出显示的速度量与给定的速度量基本相同,小幅度的波动是天线转动不平稳以及采样时间的抖动造成的。
3 结束语
与卡尔曼滤波器等算法比较,TD算法结构简单,运算量小,更适合嵌入式系统。运用TD算法得到实时准确的速度给调试、检查、测试工作提供了极大便利,同时为校正中加入微分算法,提高系统性能奠定基础。对引导值运用该算法得到引导值的速度量,可以方便地加入前馈控制,这种方法运用在某型3.7m天线系统中,通过前馈控制得到5倍以上的动态精度提升。
[1]韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.
UsingTDforantennaangularvelocitycalculation
LIQing-hua
(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)
Attennaangularvelocityisanimportantfeatureinservosystem.Whensamplingangularcycled,wecangetreal-time,smoothandaccurateangularvelocitybyasimplealgorithmusingtrackingdifferentiator(TD).
Servosystem;Angularvelocity;Trackingdifferentiat
2016-04-02
李庆华(1973-),男,河北高碑店人,工程师,主要研究方向:自动控制.
1001-9383(2016)02-0068-04
TN820
A

