圆柱亚临界-临界-超临界流动特性的大涡亚格子模型比较研究*
祝志文 邓燕华
(湖南大学土木工程学院, 长沙 410082)
圆柱亚临界-临界-超临界流动特性的大涡亚格子模型比较研究*
祝志文†邓燕华
(湖南大学土木工程学院, 长沙410082)
为获取圆柱在亚临界、临界和超临界区内的气动特征,基于大涡模拟并分别采用Smagorinsky亚格子尺度模型和动力亚格子尺度模型计算了Re=4.1×104~8.2×105内的绕流场.将获得的圆柱定常与非定常气动特性与相关文献进行了对比.研究表明,两种亚格子模型均能给出圆柱升力系数平均值、RMS值和涡脱St数的合理估计,能预测阻力系数的下降.但两种亚格子模型均无法准确预测临界区阻力系数的快速下降、不同Re数下压力系数平均和RMS值在圆柱表面的分布.在临界和超临界区,Smagorinsky亚格子尺度模型可能高估了亚格子湍流粘性;相反,动态亚格子模型可能在流场部分区域明显低估了亚格子湍流粘性.
Smagorinsky模型,动态亚格子模型,气动特性,临界区
引言
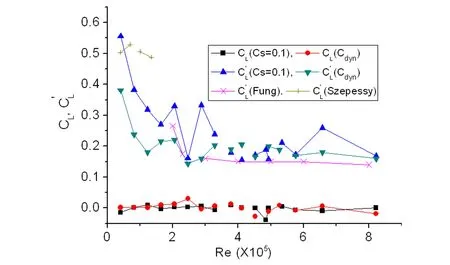
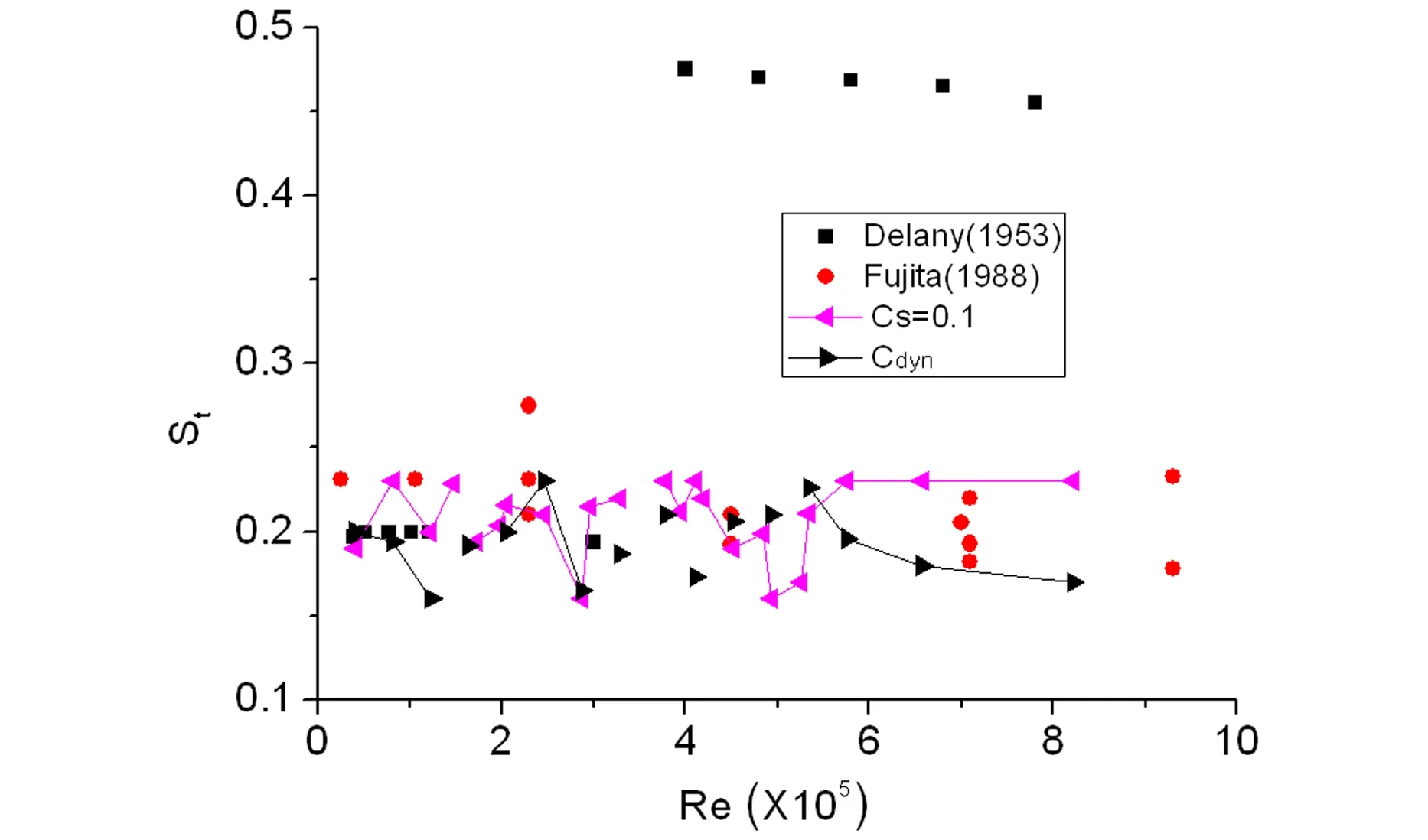
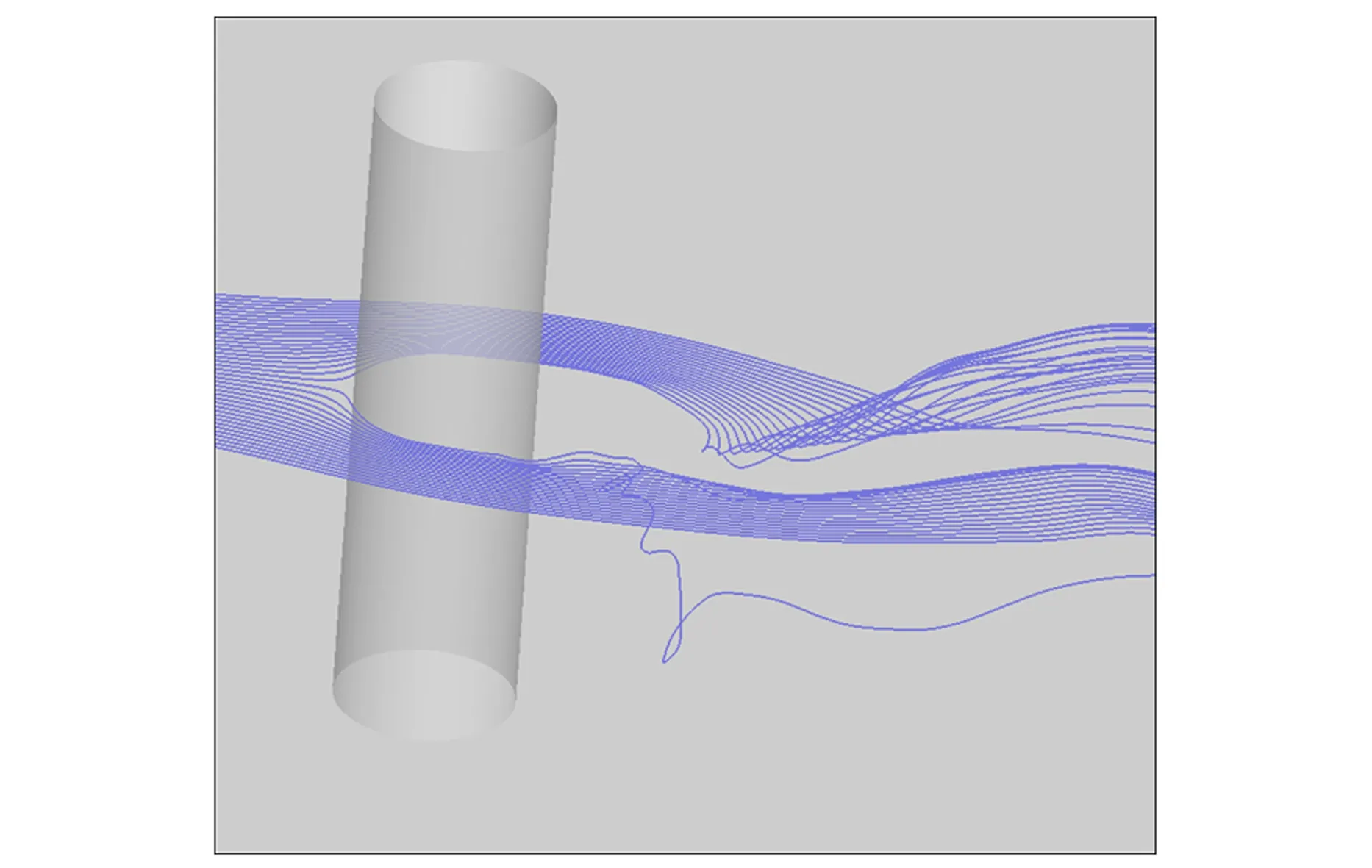
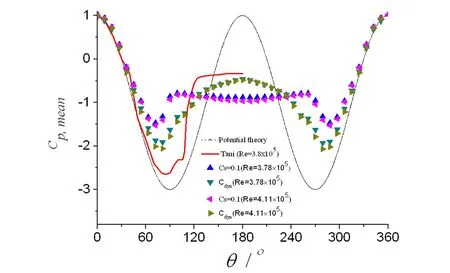
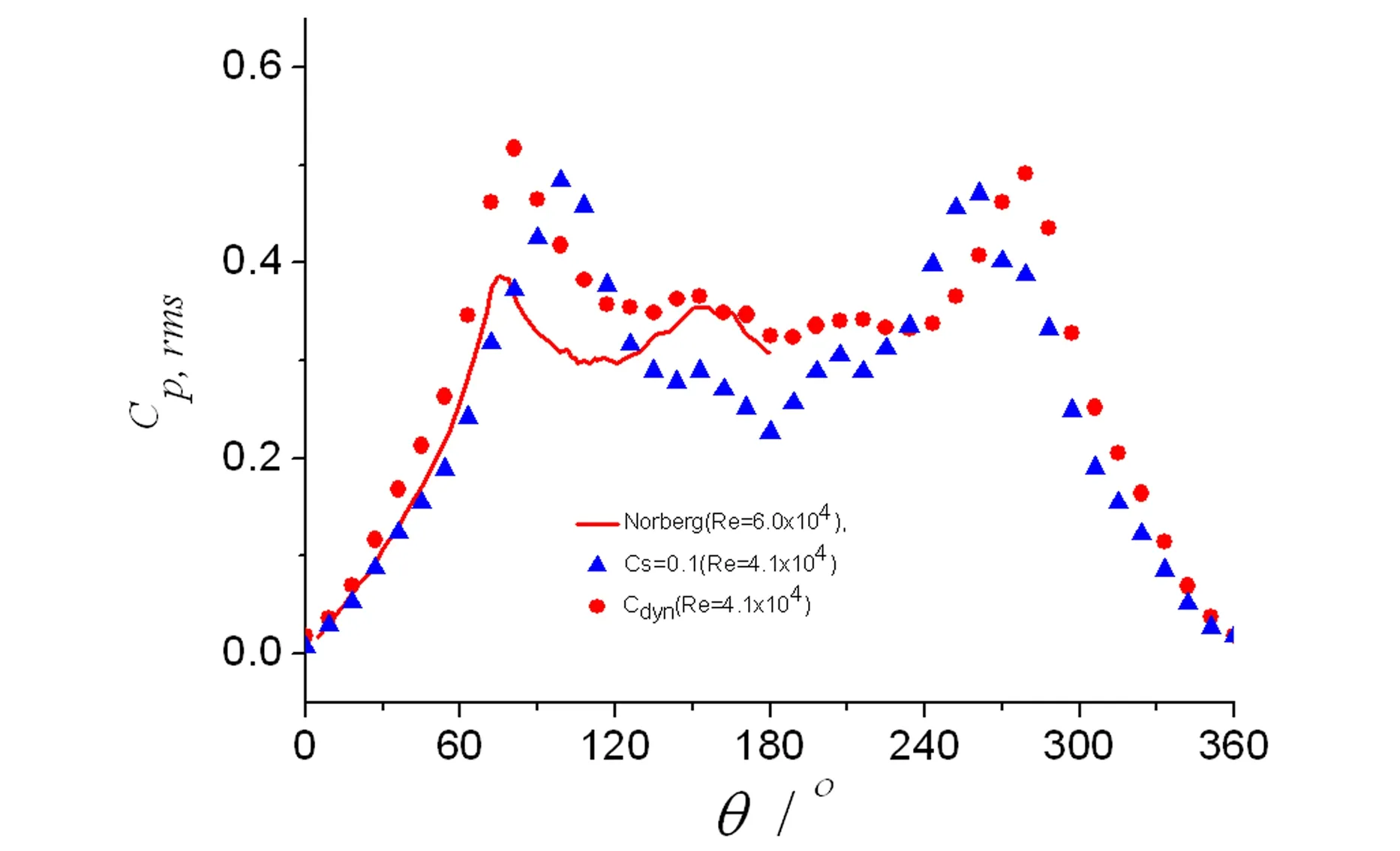
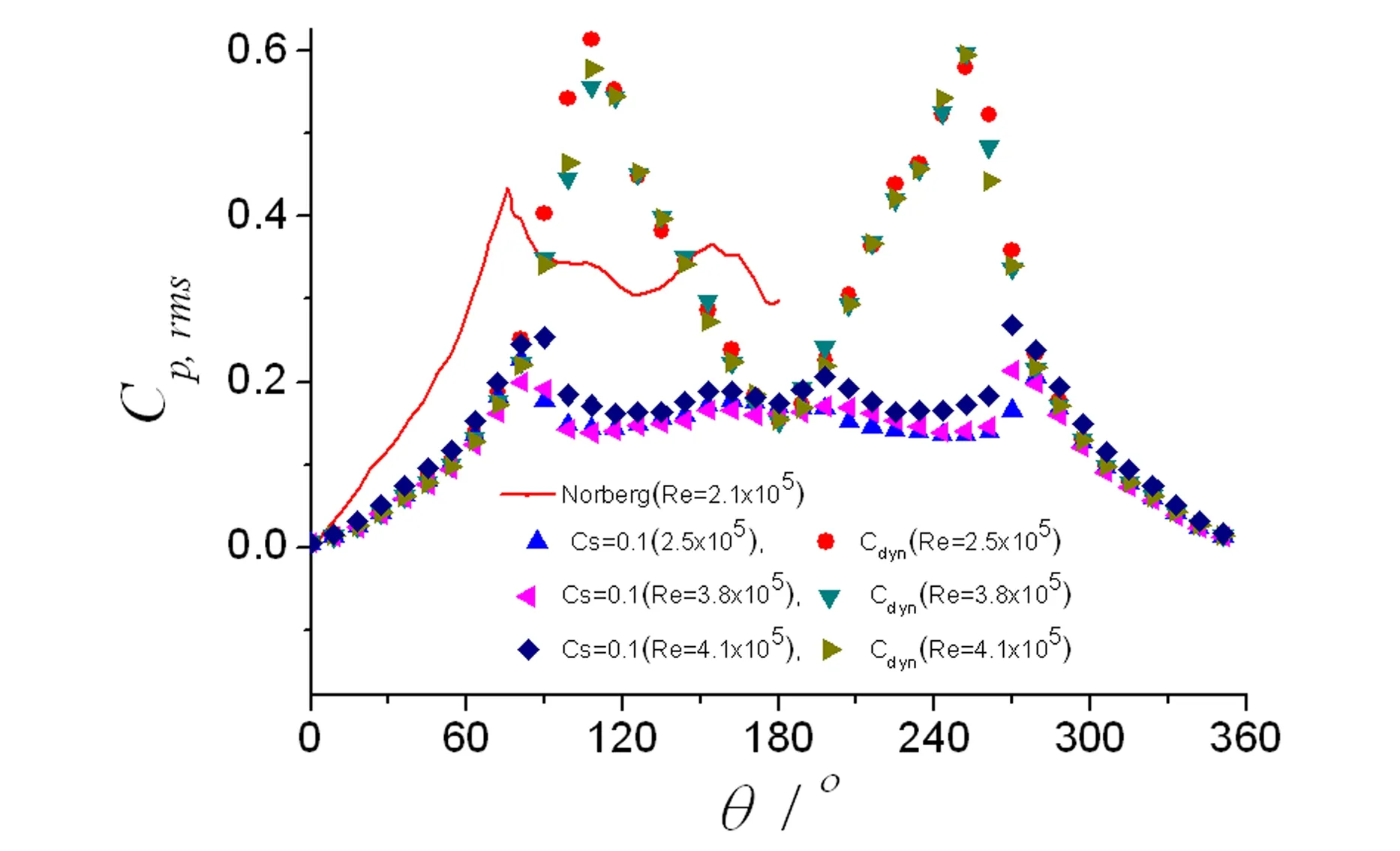
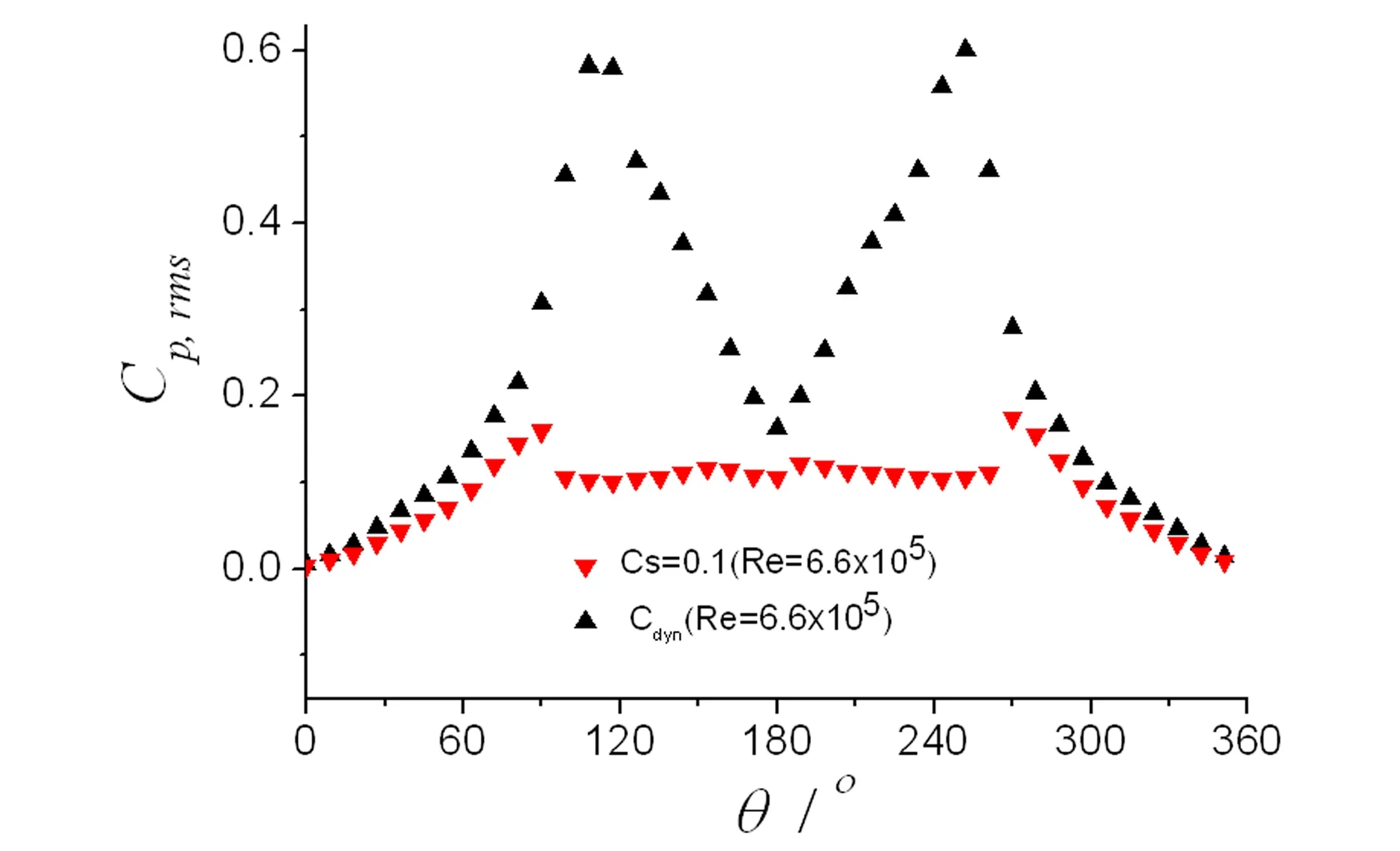
土木工程结构如主缆、桥墩、拉索和吊杆,以及电视塔、桅杆、烟囱和冷却塔,甚至一些超高层建筑都具有圆形截面特征.这些工程结构不仅会受到流体的静荷载作用,产生内力和变形,甚至可能会在周期性流体动力作用出现大幅振动现象.虽然圆柱形截面外形简单,但其绕流形态如分离点位置(θs)等随Re数的变化而不断变化(见图1),其气动力和漩涡脱落表现出很强的Re数效应[1],其流体动力学特性远比具有尖锐棱角的钝体截面复杂.一般认为,在2×105 图1 圆柱流动特性的Re数分区Fig. 1 Re number partition on flow characteristics of circular cylinder 与试验相比,数值方法能非常方便地设定和处理来流和边界条件,不存在模型支架和测量系统的干扰,因堵塞度可显著减小,可明显减少洞壁的干扰,因而在土木工程中得到了越来越多的应用[4-5].本文数值方法采用大涡模拟(LES),该方法的基本思想是[6]:基于流动中大涡和小涡的不同功能,将大涡与小涡计算分开处理.首先将小于某个尺度的旋涡从流场中过滤掉,精确求解某个尺度以上所有湍流尺度的运动,对该尺度以下的小涡采用统一的模型计算,而小涡的影响通过大涡计算来体现.LES是目前一种折中的方法,其能够捕捉许多非稳态、非平衡过程中出现的大尺度效应和拟序结构,但回避了直接数值模拟(DNS)对海量计算资源的需求问题,因而目前被认为是最具潜力的湍流数值模拟方法.本文基于大涡模拟并分别采用两种亚格子尺度模型,计算的Re=4.1×104~8.2×105,涵盖了临界区并延伸至亚临界和超临界区.获得了不同Re数下圆柱气动力系数和表面压力系数平均和RMS分布,以及漩涡脱落St数.本文研究目的是验证LES在获得圆柱阻力突降区及附近气动特性的可行性,评价不同亚格子尺度模型的性能,揭示圆柱临界Re数区及附近的流动机理. 1.1LES的两种亚格子尺度模型 LES方法需先通过对Navier-Stokes方程进行过滤,这样将流场变量分解成大尺度可直接求解部分和亚格子尺度非直接求解的模拟部分.以速度场为例,这种过滤可表示为: (1) 最早的亚格子尺度模型为Smagorinsky模型,其亚格子应力张量τij表示为 (2) (3) Smagorinsky亚格子尺度模型在很长时间内几乎没有改进,其中的模型常数Cs对各种不同的流动类型都有相对固定的最优值.但在十分复杂的钝体绕流中显然无法用一个固定的Cs值来再现各种不同的流动结构.且该模型在近壁区还需要使用在理论上难以估计的人工粘性项来获得合理的湍流行为,在各向异性流动中滤波尺度的选择也是不明确的.针对这些缺点,Germano[8]提出了引起广泛关注的动态亚格子尺度模型,该方法通过引入二次滤波函数,将二次滤波后的亚格子应力张量表示为: (4) 其中尖括号内量表示经二次滤波后的量.则介于两个滤波尺度之间的湍流应力为: (5) 其中〈τij〉为二次滤波后的亚格子应力项.如将Smagorinsky模型用于τij和Tij,得到的相应量分别表示为, (6) (7) (8) 进一步可获得动态亚格子模型常数Cdyn为: (9) 这样,由不同特征长度的两个滤波函数确定的动态亚格子模型常数Cdyn不再是常数,而是时间和空间的函数,本文称之为D模型. 1.2LES的数值实现 在本文计算的Re数范围内圆柱绕流显然是三维的[2].一般认为,不同Re数下圆柱的展向相关长度是不一样的[2],Re数越大展向相关长度越小.在建立三维计算域前,可根据展向相关长度确定数值模拟的圆柱展向长度,也即计算域的Z向尺度.由于本文Re数变化范围大,为保持计算域和网格划分的一致性,取最小Re数4.1×104经文献[2]经验公式估算的展向相关长度为3.7D,D为圆柱直径,并用于所有Re数情况. 计算域在垂直圆柱轴线的二维布置如图2所示,其中圆柱左侧Z1区为半圆柱形体域,其最左侧边界为计算域入口,采用层流速度边界条件.圆柱右侧计算域由Z2和Z3两个区组成,其中Z2采用与Z1类似的半圆柱形体域,且均采用结构化贴体“O”型六面体网格,保证了物面和外侧附近网格的完全正交性.计算域出口采用指定零值的压力边界条件.沿圆柱周向和展向分别等分为140和72个网格,采用无滑移壁面边界条件.考虑到网格无关检查的较大计算量,贴近圆柱表面的第一个网格点到物面的距离h0,通过二维CFD计算确定为h0=4.2×10-5D[7],控制网格生长率和单元正交性,以保证在流动变量变化大的区域获得高网格分辨率,在最大Re=8.2×105下计算得到的圆柱表面最大Y+数小于1(图4),保证了在所有Re数下网格分辨率满足LES的要求.整个计算域划分为1426824个单元,CFD模拟的堵塞度为1.92%,如图3所示. 图2 计算域分区和边界Fig. 2 Partition of computational domain 图3 圆柱周围网格Fig. 3 Grid arrangement around circular cylinder 在入口边界水平风速范围为U=5~100m/s,一般风速增量为2~5m/s,在Re数临界区采用小风速增量以便捕捉气动特性的快速变化;4个平行圆柱轴线和垂直圆柱轴线的计算域外平面采用对称边界条件.因不同Re下圆柱涡脱频率不同,为充分捕捉非定常特性,经时间步无关检查,确定由初步计算估算的涡脱频率,采用的迭代时间步长保证在一个涡脱周期内的时间步数不小于200步.数值模拟的其它设置同文献[7],为获得圆柱随机气动特性的合理估计,在剔除初始场计算影响结果后的涡脱周期数不小于 40.CFD模拟基于Fluent 6.3.26程序实现. 图4 圆柱壁面的Y+分布Fig. 4 Y+ value on cylinder surface 定义圆柱气动升力和阻力系数,以及漩涡脱落St数分别为: St=fsD/U (10) 其中FL和FD分别为作用在圆柱上的升力和阻力;当计算脉动量时分别对应升力和阻力RMS值;fs为圆柱漩涡脱落频率.因圆柱气动扭矩及脉动值非常小[2],本文不予考虑. 2.1气动力特征 数值模拟得到的圆柱气动力系数时程如图5~9所示,包括亚临界、临界和超临界Re数,每个Re数均给出了S模型和D模型的结果,可见气动力时程非定常特性明显.这些时程的普遍特征是升力脉动量大于阻力脉动量,S模型阻力系数明显高于D模型的结果,而前者的升力脉动量有时大于后者,有时又小于后者,表现出与Re数相关的特征. 图5 Re=1.64×105阻力和升力系数时程Fig. 5 Drag and lift coefficients when Re=1.64×105 图6 Re=2.47×105阻力和升力系数时程Fig. 6 Drag and lift coefficients when Re=2.47×105 图7 Re=3.78×105阻力和升力系数时程Fig. 7 Drag and lift coefficients when Re=3.78×105 图8 Re=4.52×105阻力和升力系数时程Fig. 8 Drag and lift coefficients when Re=4.52×105 图10是在临界区Re=3.78×105时升力系数时程的功率谱密度(PSD)分析,分析均基于相等的数据个数.虽然两种亚格子模型均能给出多个St数的估计,但S模型的峰值能量更大,其它频率点能量小,但D模型给出了更多较高能量的低频成分,导致峰值St数的显著占优度下降. 图10 Re=3.78×105 升力系数时程对St数的PSDFig. 10 PSD-St number curves for lift coefficient records when Re=3.78×105 图11是模拟的阻力系数平均值随Re数的变化曲线,并与试验结果进行了对比.可见两种亚格子模型均能反映阻力系数的下降,但二者开始下降的Re数均明显早于Re=2×105,而阻力系数平均值下降的幅度没有试验结果大,也即不是在临界区的突降.另外,S模型的阻力系数下降幅度也没有D模型下降幅度大.图12是升力系数平均值和RMS值随Re的变化,可见升力系数平均值在模拟的全部Re数上,没有出现文献[3]报道的临界区非零均大升力值情况,可认为升力系数时均值为零.升力系数RMS值在Re数小于2×105时,均小于Szepessy[12]的结果,但当Re数大于2×105时,本文两种亚格子模型的升力系数RMS值均大于Fung[9]的试验结果.上述差别的原因,可能是来流和试验条件、圆柱展向长度、试验测量等原因,也可能是LES的两种亚格子模型在圆柱临界区及附近复杂绕流模拟上的不足.与试验一样,本文两种亚格子模型均能给出圆柱涡脱的多个St数估计,图13是两种亚格子模型获得的峰值St数随Re数变化,以及与相关文献的报道, 可见本文St数与试验结果的一致性较好.图14是从圆柱展向中截面的圆柱上游出发的流线,明显可见圆柱尾迹的显著三维流效应. 图11 阻力系数平均值随Re的变化Fig. 11 Mean drag coefficient-Re number relationships 图12 升力系数平均值和RMS值随Re的变化Fig. 12 Mean and RMS drag coefficient-Re number relationships 图13 St数随Re数变化的比较Fig.13 Comparison of St number-Re number curves 图14 从圆柱中截面上游出发的流线Fig. 14 Streamtraces starting at windward side of cylinder central-span section 2.2圆柱表面平均和脉动压力分布 为评价两种亚格子模型在预测圆柱表面平均和脉动压力系数分布上的合理性,本文在圆柱展向的中截面上,沿圆柱表面周向均匀布置40个压力监测点,压力监测点编号和对应的圆心角定义如图15所示.按下式计算压力系数: Cp=(P-P0)/(0.5ρU2) (12) 其中P0为参考压力,本文取为零;P为监测点;Cp的统计值分为压力系数平均值Cp,mean和脉动值Cp,rms. 图15 圆柱中截面压力监测点Fig. 15 Pressure taps on the middle cross section of cylinder 图16~18是监测点压力系数平均值在圆柱中截面上的分布,并与势流理论[2]和试验结果进行了对比.可见压力系数平均值在圆柱上下表面表现了较好的对称性,因此圆柱的升力系数平均值为零.从试验值来看,在不同的Re数下压力系数平均值分布曲线形状相同,均显示一个以底部为中心的平台,但不同Re数这个平台的宽度不一样,且平台的压力值随Re数的增大而增大,导致圆柱阻力系数平均值快速降低. 图16 亚临界压力系数平均在圆柱表面分布Fig. 16 Distribution of subcritical pressure coefficient on cylinder in sub-critical regime 图17 临界压力系数平均值在圆柱表面分布Fig. 17 Distribution of critical pressure coefficient on cylinder in trans-critical regime 图18 超临界压力系数平均在圆柱表面分布Fig. 18 Distribution of supercritical pressure coefficient on cylinder in super-critical regime 在所有Re数下,D模型预测的分离点在S模型的下游,且分离点前后的压力系数平均值也明显小于S模型预测值.在三个区,S模型均给出了与试验相同趋势的平均压力系数分布,但亚临界下压力系数的平台值大于试验值,由于随Re数的增大该平台值增大较慢,因此在临界和超临界明显小于试验值,这是导致阻力系数没有出现快速下降的原因.D模型的压力系数平均值分布曲线形状更像势流理论解,在所有Re数下均没有预测出平台曲线.且由于底部压力系数明显大于S模型结果,因此在计算的所有Re数下其阻力系数均小于S模型结果. 图19~21是监测点压力系数RMS值在圆柱中截面上的分布.在亚临界区,两种亚格子模型预测的压力系数RMS值分布与试验结果有相同的趋势性,但峰值RMS值均大于试验值.D模型预测的圆柱底部压力系数RMS值大于S模型值.在临界区,两种模型预测的压力系数RMS值也与实验结果有相同的趋势,在三个Re数下,同一模型预测的压力系数RMS分布非常一致,但从图20来看,D模型和S模型预测的最大RMS值差别很大,D模型值明显大于试验结果,但S模型明显小于试验值,且底部压力系数RMS值也均明显小于试验值.从图21可见,超临界两种模型预测的压力系数RMS值在圆柱表面的分布与临界情况相同,只是S模型的预测值进一步减小.这表明,S模型和D模型均可能 图19 亚临界压力系数RMS值在圆柱表面分布Fig. 19 Distribution of subcritical pressure coefficient RMS on cylinder in sub-critical regime 图20 临界压力系数RMS值在圆柱表面分布Fig. 20 Distribution of subcritical pressure coefficient RMS on cylinder in trans-critical regime 图21 超临界压力系数RMS值在圆柱表面的分布Fig .21 Distribution of subcritical pressure coefficient RMS on cylinder in super-critical regime 未能给出计算域空间点上合理的亚格子湍流粘性估计,在临界和超临界区S 模型可能高估了亚格子湍流粘性,而D 模型可能在圆柱周围部分区域明显低估了亚格子湍流粘性. 本文基于LES的两种亚格子模型,模拟了亚临界、临界和超临界Re数下圆柱绕流场,通过其气动特性的研究,得到下述结论: 1) 两种亚格子模型能一定程度地预测阻力系数Re数增大而减小的特征,能给出升力系数平均值与RMS值和涡脱St数的合理估计,能反映圆柱流动的非定常和三维尾迹特征. 2) 两种亚格子模型预测的圆柱平均升力系数在所有Re数下均接近零,但均不能准确预测阻力系数临界区的大幅突降特征. 3) 在所有Re数下,S模型均给出了与试验相同形状的平均压力系数分布曲线,但曲线平台值与试验有较大差别;动态亚格子模型给出的平均压力系数分布曲线形状类似势流理论解,没有试验结果的平台特征. 4) 在临界和超临界区,Smagorinsky亚格子尺度模型可能高估了亚格子湍流粘性;相反,动态亚格子模型可能在流场部分区域明显低估了亚格子湍流粘性. 1Zdravkovich M M. Flow around circular cylinders. Volume 1: Fundamentals, Oxford University Press,New York, 1997 2Norberg C. Fluctuating lift on a circular cylinder: review and new measurements.JournalofFluidandStructures,2003,17(1):57~96 3刘庆宽,乔富贵,张峰. 考虑雷诺数效应的斜拉索气动力试验研究. 土木工程学报,2011,44(11):59~65 (Liu Q K, Qiao F G, Zhang F. Experimental study on cable aerodynamic forces considering Reynolds number effect.ChinaCivilEngineeringJournal,2011,44(11):59~65 (in Chinese)) 4Zhu Z W, Gu M. Identification of flutter derivatives of bridge decks using CFD-based discrete-time aerodynamic models.WindandStructures,AnInternationalJournal,2014,18(3):215~233 5祝志文. 超临界雷诺数下拉索顺风向自激力特性研究. 振动工程学报,2014,27(3):377~384 (Zhu Z W. Characteristics of along-wind self-excited forces of a cable under super-critical Reynolds number.JournalofVibrationEngineering,2014,27(3):377~384 (in Chinese)) 6Smagorinsky J. General Circulation Experiments with the Primitive Equations.MonthlyWeatherReview,1963,91(3):99~164 7祝志文. 圆柱高Re数绕流特性的大涡模拟研究. 振动工程学报,2014,27(1):51~59 (Zhu Z W. Large eddy simulation of flow around circular cylinder under high Reynolds number.JournalofVibrationEngineering,2014,27(1):51~59 (in Chinese)) 8Germano M, Piomelli U, Moin P, Cabot W H. A dynamic subgrid-scale eddy viscosity model.PhysicsofFluids,A:FluidDynamics,1991,3(7):1760~1765 9Fung Y C. Fluctuating lift and drag acting on cylinder in a flow at superciritical Reynolds numbers.JournalofAeronauticalSciences,1960,27(11):801~804 10Farell C, Blessmann J. On critical flow around smooth circular cylinders.JournalofFluidMechanics,1983,136(1):375~391 11Guven O, Farell C, Patel V C. Boundary-layer development on a circular cylinder with ribs.JournalofFluidEngineering,1983,105(2):179~184 12Szepessy S, Bearman P W. Aspect ratio and end plate effects on vortex shedding from a circular cylinder.JournalofFluidMechanics,1992,234(1):191~217 13Delany N K, Sorensen N E. Low speed drag of cylinders of various shapes. NACA TN 3038,1953 14Fujita K, Ikegami Y, Kobayashi K, Ohashi M. Experimental studies on fluctuating lift force on a single circular cylinder at high Reynolds numbers.JapanJournalofWindEngineering,1988,37(2):73~82 15Achenbach E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re=5×106.JournalofFluidMech.,1968,34(4):625~639 16Tani I. Low speed flows involving bubble separations. Progress in Aerospace Science,1964,5:70~90 *The project supported by the National Natural Science Foundation of China (51278191), National Key Basic Research Program of China(2015CB0577,2015CB057701) † Corresponding author E-mail: zwzhu@hnu.edu.cn 17 July 2014,revised 07 October 2015. COMPARATIVE STUDY OF SUBGRID LARGE EDDY MODELS ON FLOW PREDICTION OF CIRCULAR CYLINDER IN SUBCRITICAL-CRITICAL-SUPERCRITICAL REGIME* Zhu Zhiwen†Deng Yanhua (CollegeofCivilEngineering,HunanUniversity,Changsha410082,China) In order to obtain the aerodynamics of the circular cylinder in subcritical-to-supercritical flow regime, the large eddy simulations (LES) with the smagorinsky subgrid scale and dynamic subgrid scale models are respectively employed to predict the flow field where Re is from 4.1×104~8.2×105. The obtained steady and unsteady aerodynamics are compared with available data in other references. The results show that both subgrid scale models provide reasonable estimation on mean and RMS lift coefficients, vortex shedding St number and drop of drag coefficients. However, the drag crisis in critical regime is not accurately predicted, but reasonable estimation on mean and RMS pressure distribution around the cylinder is obtained. In critical and supercritical regimes, the smagorinsky subgrid scale model may overestimate the subgrid turbulent viscosity, while the dynamic subgrid scale model may significantly underestimate the subgrid turbulent viscosity in some areas of the flow field. circular cylinder,Smagorinsky subgrid scale models,dynamic subgrid scale models,aerodynamics,critical regime E-mail: zwzhu@hnu.edu.cn 10.6052/1672-6553-2015-80 2014-07-17收到第1稿,2015-10-07收到修改稿. *国家自然科学基金资助项目(51278191)和国家重点基础研究发展计划(2015CB057702,2015CB057701)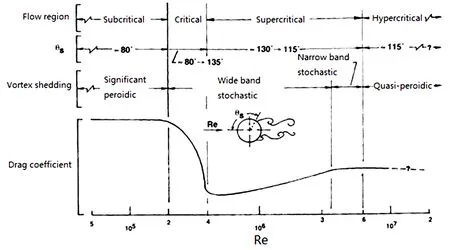
1 控制方法及数值实现









2 数值结果与讨论









5 结论

