基于非线性约束污水处理曝气池过程的优化*

葛福婷, 张　秀,王家豪,朱家明

(1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 金融学院，安徽 蚌埠 233030)



基于非线性约束污水处理曝气池过程的优化*

葛福婷1, 张秀1,王家豪2,朱家明1

(1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 金融学院，安徽 蚌埠 233030)

针对污水处理曝气池过程中关于COD问题的优化，通过定量分析、相关分析、变量控制等方法，建立了主成分分析、时间序列分析、非线性预测、SQPM非线性约束等模型，得到了活性污染泥浓度和氧化还原位点对出口COD的时间延迟影响程度最大,出口COD的最优非线性预测函数，为使COD浓度稳定在一定水平各指标浓度调节额等结论.

污水处理；COD；主成分分析；时间序列分析；非线性预测；SQPM非线性约束

0　引言

近年来，关于水污染的话题不断被提起，2014年9月有媒体曝光内蒙古和宁夏交界处的腾格里沙漠存在企业非法排污现象[1]，已对周围环境造成污染，引起大家对水污染严重程度的广泛关注和民众环保意识的觉醒.污水处理被广泛运用于建筑、农业、医疗等各个领域，最常用的污水处理方法为活性污泥法，通过曝气池处理搅拌混合液使泥、水充分接触和向微生物供氧.化学需氧量(COD，Chemical oxygen demand)是污水处理最重要的处理指标，用来表明在出水或纯净水中还有多少残留的有机污染，对污水处理质量、资源的合理运用等因素有着十分密切的联系.根据已有数据，运用数学建模的方法，对污水处理曝气池过程进行科学合理的评价、预测和分析，是一个很有实用价值的问题.

1　数据来源与模型假设

数据来源于2015年安徽财经大学暑期数学建模模拟题4[2]中2014年1月1日至2014年6月30日某污水处理厂污水处理观察数据共22032组.为了便于解决问题，提出以下假设：1)污水处理曝气池过程中有良好的活性污泥和充足的氧气；2)微生物分解通过氧化阶段，除去了所吸附的大量有机物后，污泥又重新出现活性，恢复吸附氧化分解能力[3]；3)不考虑实际观察中存在的有机物浓度增加时，微生物增长速率变化的滞后效应[4]；4)仅考虑所给的数据指标对COD浓度的相关问题的研究；5)各个鼓风机出口与入口指标间处于并列的关系；6)系统建模过程中,均不考虑污染组分的积累,即视系统为稳定状态,只考虑系统输入、输出项和反应项,积累项为0[5]；7) 污水处理系统运行时温度视为恒定，pH值恒定而且接近中性.

2　污水处理曝气池过程COD时间延迟相关分析

2.1研究思路

我们要研究的是，污水处理曝气池过程中各类参数对出口COD的时间延迟关系，并进行结果输出.对此可以入、出口COD差值替代COD为因变量，其他各参变量为自变量，结合污水处理的周期性，进行研究.首先，计算各类参数对COD的Pearson相关系数，得到时间延迟分析的作用方向和程度大小；然后着重分析COD与6类参数之间的相关关系，采用主成分分析法计算出各参数对COD的贡献率大小，以检验相关系数结果的准确性；最后，综合前面的分析结论，做COD时间延迟的相关分析和独立分析.建模流程图如图1所示.

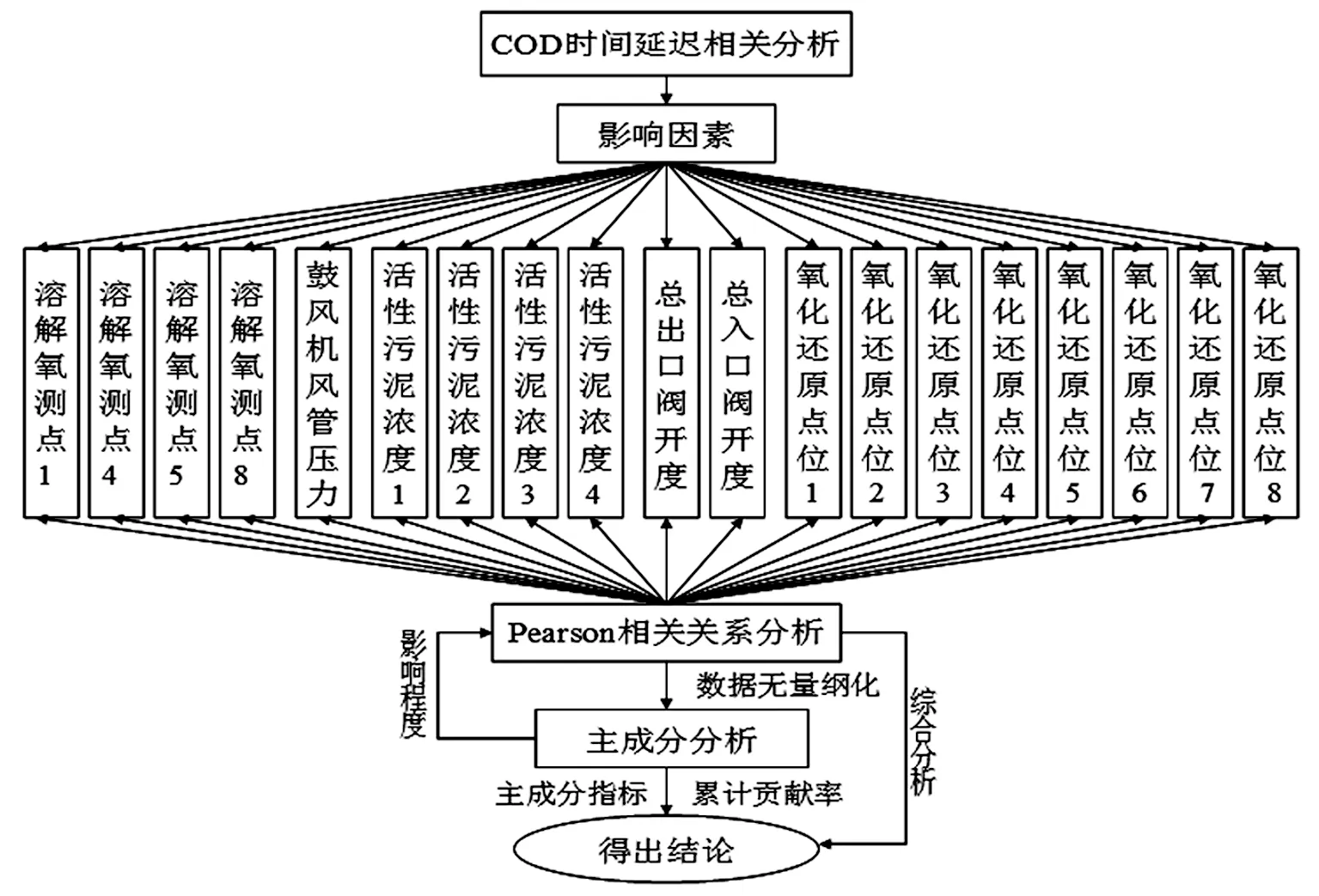
图1　COD时间延迟相关分析建模流程图

2.2数据处理

2.2.1源数据分析

污水处理过程中存在一定的耗氧量，故可用入、出口COD的差值来近似替代出口COD；入口COD保持不变的时候恰是微生物的氧化还原分解反应过程，且每一个入、出口COD数值呈周期性变化，每隔12个检测单位(即2小时)基本相同，即下一周期COD数据是上一周期氧化还原反应结果的表现.

2.2.2剔除周期性波动

删除第一组12个相同数值的出口COD的数据，依次将其他各时刻的出口COD数值向前顺延2小时，得到源时间序列数据.

2.2.3数据预处理

在源时间序列数据上，为构建合理、完整的评价体系，除大部分可直接用于处理的指标外，还需再计算入、出口COD的差值，总出口阀开度和总入口阀开度.计算公式如下：

入出口COD差值：ai-bi；

总出口阀开度：∑ci；

总入口阀开度：∑di

其中，ai表示入口COD，bi表示出口COD，ci表示各鼓风机出口阀开度，di表示各鼓风机出口阀开度，i表示各参数污水处理检测的时刻编码.

2.2.4Pearson相关系数分析

对可能影响COD数值的6类参数(共19个指标)无量纲化，运用MATLAB软件，求解各指标对COD的Pearson相关系数P[6]，计算公式如下，结果如表1所示.

P用来衡量COD浓度分别于各个指标间线性关系的强弱，其取值范围为[0,1].其中，m表示COD浓度数据序列，n表示其他各影响因素数据序列，N为样本个数，P的绝对值越大，相关性越强.

2.2.5主成分分析

为进一步定量化描述各指标对COD的时间延迟影响程度，基于主成分分析法[7]研究思路，对数据进行标准化处理，运用MATLAB软件编程，得到各指标对COD时间延迟的贡献率及排名，结果见表2.

2.2.6研究结论

结合Pearson相关系数检验及主成分分析的结果，综合各指标对COD时间延迟结果的独立相关分析及总体相关分析，即可得出污水曝气池处理过程中各指标对COD时间延迟影响程度及作用方向.

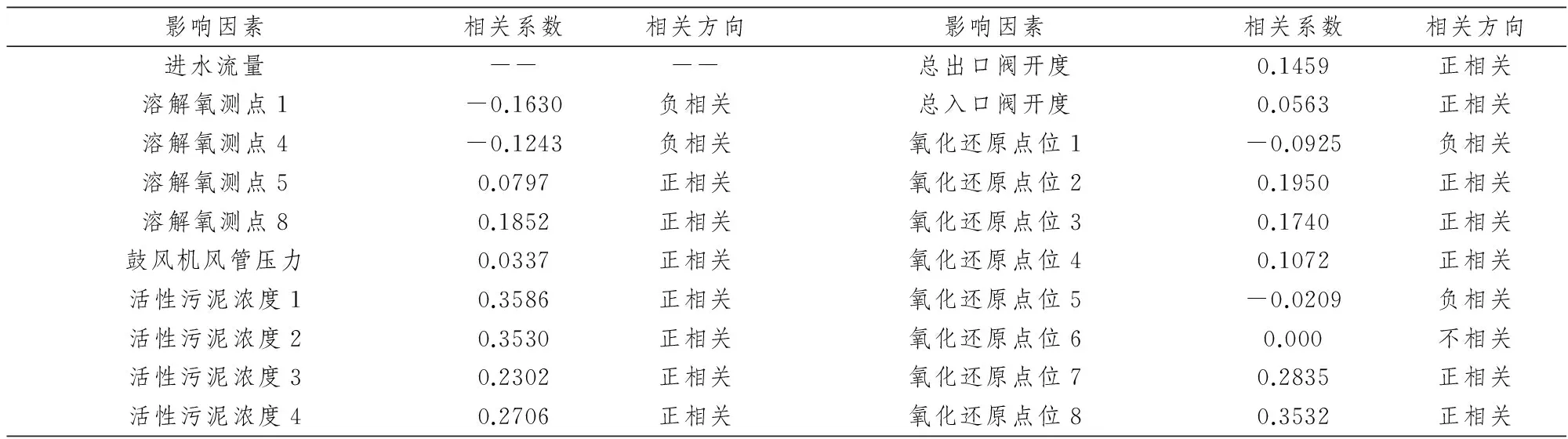
表1　各指标对COD的时间延迟的相关系数

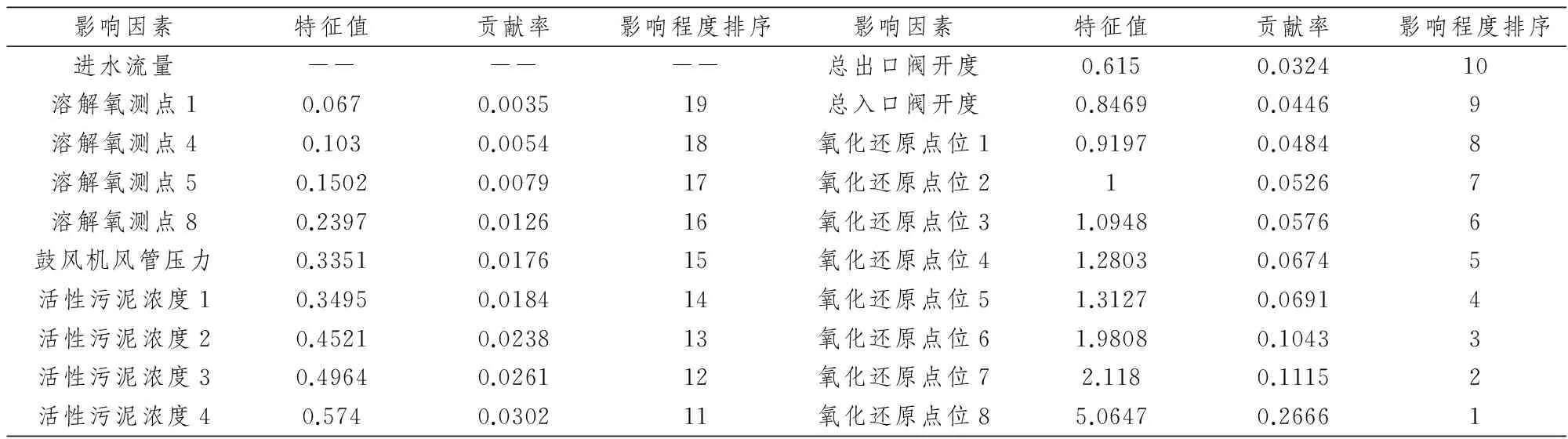
表2　各指标对COD的时间延迟的贡献率

2.3结果分析

Pearson相关关系分析中：COD的时间延迟与指标溶解氧测点1、溶解氧测点4、氧化还原点位1、氧化还原点位5呈负相关，即这些指标浓度越大，出口COD浓度越小，反之，指标浓度越小，出口COD浓度越大，但相关性很小，可能是在污水处理曝气池过程(如图2)中，这些指标担当了微生物的氧化还原反应氧化剂的作用，促进供给物氧化分解所需的氧气；其他指标对COD的时间延迟均呈正相关，说明这些指标直接或间接地参与了污水处理的氧化还原反应，促进COD的氧化还原分解成微毒或无毒的物质.特别地，活性污泥浓度1、活性污泥浓度2和氧化还原点位8与COD的时间延迟相关关系最大，其中活性污泥浓度1的相关系数高达0.3586.

主成分分析中：兼顾选取指标个数和累计贡献率两个方面，选取指标使得累计贡献率达到85%以上为止.筛选得氧化还原点1～8、总出口阀开度和总入口阀开度共10个指标，建立与COD的时间延迟相关关系函数如下：

COD=0.0484ω1+0.0526ω2+0.0576ω3+

0.0674ω4+0.0691ω5+0.1043ω6+0.1115ω7+

0.2666ω8+0.0324c+0.0446d

其中，ωk(k=1,2,…，8)分别表示氧化还原点位1～8，c，d分别表示总出口阀开度和总入口阀开度.

综合上述的研究结论，活性污染泥浓度和氧化还原点位对COD的时间延迟影响程度较大，它们对时间延迟的作用表现在参与反应池中的反应，以充当还原剂或形成难以反应的保护膜抑制或阻碍氧化反应的发生.特别地，氧化还原点位8对COD的时间延迟的影响程度高达0.2666，可能是由于该指标是污水处理的氧化还原反应主要的作用点，有更难氧化还原的有害粒子或物质.

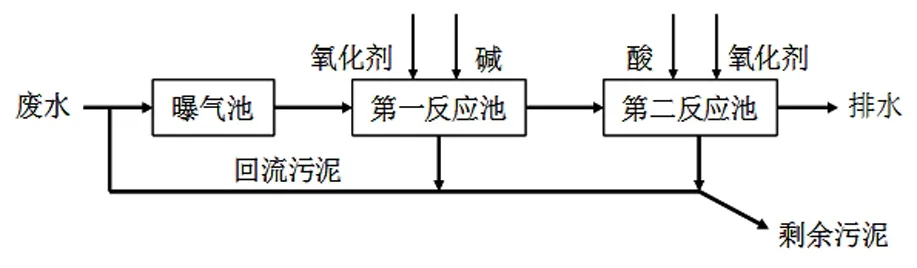
图2 活性污泥法基本流程

3　非线性规划时间序列水质预测

3.1研究思路

河流水质表达的本质是关于“污染物量”与“水量”的二元函数，河流天然“水量”的年际变化影响，远远大于人类的排放活动对河流水质的影响，需要约束的是“污染物量”的排放。

我们要研究的是，联系出口COD时间延迟关系，建立各参数对出口COD的非线性时间预测模型[8].通过对入口COD的时间分析，发现各指标浓度呈显著的季节变动[9]和长期趋势[10]，考虑到由于季节变动和长期趋势可能造成的系统误差，我们分别拟合出每个指标与出口COD的非线性时间序列函数，判断各类拟合函数的可决系数R2大小，选择最优拟合函数.这样一方面很好地减少了系统误差对周期性波动的影响，另一方面也通过控制变量达到预测出口COD的目的，揭示了出口COD浓度时间序列变化的规律性，为经济预测提供依据.

3.2数据处理

运用EXCEL软件，绘制入口COD浓度随时间变化的散点图，如图3所示.

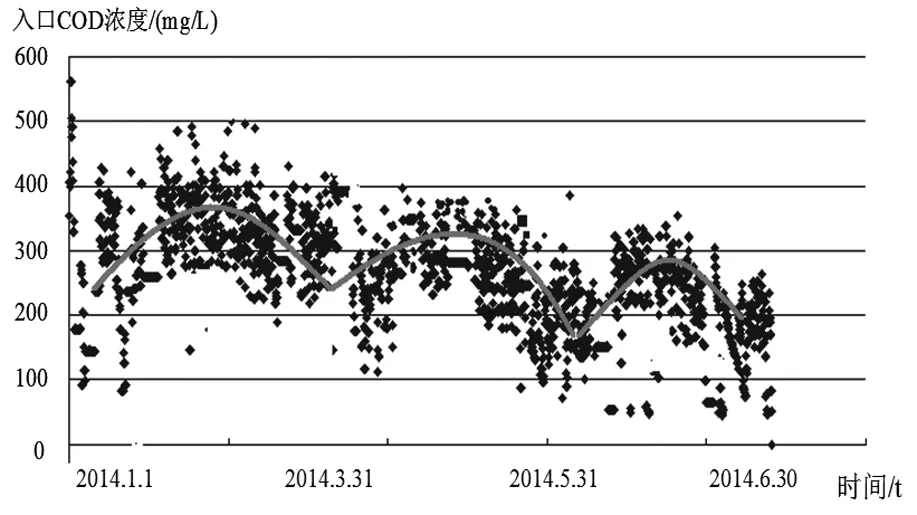
图3　入口COD变化趋势

通过图3，不难发现入口COD浓度呈现周期性的变化，每两个月入口COD浓度变化幅度相同，为研究方便，可选取某一周期的数据进行拟合分析，其他各周期变化类似，假使选取3～5月的数据.

同时，入口COD、溶解氧测点和活性污泥浓度存在负值，与实际情况不符，剔除该类数据.此外，有些数据的值基本保持不变，如鼓风机风管压力和氧化还原点位6，说明其浓度不受其他因素影响，故对这两组变量不做分析.

1)3σ准则剔除异常数据. 由于数据的检测可能存在检查分析和设备故障导致的误差，所给各指标的原始数据通常存在少数的异常数据，从而对非线性规划水质预测模型整体性能产生影响.因此，本文首先采用假设检验中的3σ准则对异常数据进行处理，即当某一检验数据的偏差满足3σ准则，则视其为异常数据，予以剔除.公式如下：

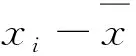
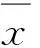
对COD浓度时间序列进行归一化处理，归一化后数据的取值在[-1,1]之间，归一化的公式为

Yn=(Y-Miny)/(Maxy-Miny)

其中，Y为原始COD浓度数据，Yn为归一化后的COD浓度数据，Miny为Y的最小值，Maxy为Y的最大值.

3)最大判定系数R2.

运用SPSS软件，分别拟合出各个指标对出口COD的时间序列分析函数[11]，介于文章篇幅有限，仅给出溶解氧测点1和氧化还原位点3对COD的时间序列分析结果，见表3和表4.

表3　溶解氧测点1对COD的时间序列分析函数

表4　氧化还原位点3对COD的时间序列分析函数

在所研究的污水处理周期中，不同拟合函数下t检验的p值取值均为0，即均通过假设检验，进一步说明了数据的拟合是合理的.其中，最大判定系数R2相应的函数即为出口COD时间序列分析的最优函数关系式，进一步筛选分析，即可得出结论.

3.3结果分析

剔除不作讨论的鼓风机风管压力和氧化还原点位6指标，分析筛选得17个指标下的最优时间序列函数，如表5所示.

表5　各指标对出口COD的最优时间序列函数

通过SPSS分析的结果，可以看出整体拟合效果较好，判定系数R2最低为0.44，最高达0.89,且总体上以三次函数拟合效果最佳，绝大多数函数的拟合优度达到0.75以上.根据拟合出的最优时间序列函数，可用曲线拟合方法对系统进行客观的描述.此法相较于神经网络等在非线性时间序列预测中的应用[12]，可操作更强、约束条件较少、适用范围更广.同时，可调整输入指标使COD浓度保持在目标值上，即预测到COD浓度要偏离目标时便可进行必要的控制，这对稳定COD数值在正常范围内、合理有效监控污水处理质量尤为重要.

4　不同影响因素对COD的非线性约束

4.1研究思路

我们要探究的是，在污水处理曝气池过程中，为使COD的浓度维持在某一固定的水平，该如何对各个指标浓度进行调节.参照各指标关于出口COD的最优时间序列函数，引入对出口COD浓度的目标值约束，结合SQPM非线性规划，反复迭代求解得各指标最低浓度限额；最后，分析目标约束下，各个指标浓度所能取的最小值，并结合实际情况，从而得到目标约束下，各个指标浓度对COD浓度介稳作用的取值范围.

4.2数据处理

依据《中华人民共和国水污染防治法》所规定的污水综合排放标准中COD浓度的排放标准[13]，假使控制COD的取值在35 mg/L的较理想水平.参照关于出口COD最优时间序列分析的结果，基于模型建立的合理性和结论的最优化，选择了SQPM(Sequential Quadratic Programming Method,序列二次规划方法)的非线性规划算法[14]，通过一系列的迭代计算逼近原带约束非线性规划问题,使迭代收敛到极值点的各指标的最小浓度值.

对17个参变量指标赋予变量名x1,x2,x3,…,x17，并对出口COD-y进行约束，建立非线性规划规划模型：

运用MATLAB软件编程[15]，得各个指标符合限制COD浓度所要求的最小值，见表6.

表6　各指标约束COD浓度要求的最小值

参照各指标约束COD浓度要求的最小值，并结合不同条件下，各指标实际取值情况，即得维持COD浓度在目标值所需的最低条件.同时，为详细探究各指标单独控制COD浓度大小的作用机制，可引用多准则多目标水平(MC2)的非线性规划[16]理论及研究方法，鉴于文章篇幅有限，不再赘述.

4.3结果分析

如表6，为限制COD浓度至多达到35 mg/L其他影响因素必须同时达到的最低浓度，如活性污泥浓度1的浓度至少要达到5.275756568 mg/L，氧化还原点位2的浓度至少要达到-97.76912439 mg/L等，这里的负值表示氧气的消耗量大小，反映该指标在污水处理过程中充当氧化剂作用的强度大小.显然，某些指标往往无法达到各自的最低浓度，而是本身就存在一个限额区间，即最低浓度区间.这时，需要联系实际，选择各指标合理的浓度范围，以保持COD浓度水平稳定在正常范围，保证水源的质量和人们身体健康水平.SQPM的非线性规划算法通过一系列的迭代逼近、使迭代收敛到极限值是该算法的亮点，它能很好地解决单准则多目标非线性规划问题，有较强的可操作性和实际应用价值，但对多准则多目标问题的解决存在一定局限性.

5　结语

文章针对活性污泥法污水处理曝气池过程中问题的优化，运用多种方法建立模型，使问题得到了更加全面的分析.随着研究的深入以及数据的合理化处理,可以直观、定量的显现出各影响因子间的关系和作用机理.本文也运用多种软件给出各种相关图形，通过对数据的处理、模型的分析，使结果更形象易懂.量化处理的不同影响因素与COD浓度的时间序列延迟关系和介稳性，巧妙地将不同指标与COD间的模糊关系具体化，也为最大效益化利用资源提供了参考；同时，也警示大众在城市化和社会化不断加剧的社会现状下也要注重对水资源的合理排放处理和生态可持续发展.在大力提高自己生活质量的同时，也要将合理排放和处理水污染作为一种自觉的行为.

[1]新华网.宁夏一家化工企业向腾格里沙漠非法排污被关停[EB/OL].http://news.xinhuanet.com/legal/2014-09/09/c_126965852.htm.

[2]2015年安徽财经大学暑期数学建模模拟题4[EB/OL]. http://zhujm1973.blog.163.com/blog/static/31551355201591310512845/

[3]魏海涛,刘响江,李涛.活性污泥法处理生活污水、废水综述[J].河北电力技术,2005,24(4):36-37.

[4]于广平，苑明哲，王宏.活性污泥法污水处理数学模型的发展和应用[J].信息与控制,2006,35(5):615.

[5]庞子山.活性污泥法工艺系统优化设计模型及应用研究[D].重庆:重庆大学,2004:53-54.

[6]蒋辉,邓伟民,陈晓青.基于Pearson系数与多元核支持向量分类的葡萄酒分析[J].农业机械学报,2014,45(1):203-205.

[7]齐敏芳,付忠广,景源,等.基于信息熵与主成分分析的火电机组综合评价方法[J].中国电机工程学报,2013,33(2):59-62.

[8]米莎,韦安磊,王小文,等.污水处理厂水质时间序列的BP神经网络预测模型研究[J].资源环境与发展,2012,2:43-45.

[9]百度百科.季节变动预测法[EB/OL].http://baike.baidu.com/view/2201425.htm.

[10]好搜百科.长期趋势[EB/OL].http://baike.haosou.com/doc/5612100-5824710.html.

[11]霍露萍.中国主要果蔬消费量预测[J].农业消费展望,2014,6(1):76-79.

[12]道客巴巴.径向基函数神经网络在非线性时间序列预测中的应用[EB/OL].http://www.doc88.com/p-909599325254.html.

[13]全国人民代表大会常务委员会.污水综合排放标准[EB/OL].http://baike.haosou.com/doc/548419-580566.html.

[14]范东明.非线性最小二乘参数平差的非线性规划算法研究[J].西安交通大学学报,2001,36(5):478-480.

[15]周凯，宋军全，邬学军.数学建模竞赛入门与提高[M].杭州：浙江大学出版社,2011.

[16]陈丹丹.多准则多约束水平非线性规划理论及应用研究[D].四川:西南石油大学,2014:16-25.

[责任编辑苏琴]

[责任校对黄招扬]

Optimization of Aeration Tank Process based on Nonlinear Constrained Wastewater Treatment

GE Fu-ting1, ZHANG Xiu1, WANG Jia-hao2, ZHU Jia-ming1

(1.SchoolofStatisticsandAppliedMathematics,AnhuiUniversityofFinanceandEconomics,Bengbu233030,China；2.SchoolofFinance,AnhuiUniversityofFinanceandEconomics,Bengbu233030,China)

For sewage aeration pool of COD problem in the process of optimization, through quantitative analysis, correlation analysis, variable control method, establishing the principal component analysis, time series analysis and nonlinear prediction, SQPM nonlinear constraint model, got the active mud pollution concentration and the REDOX sites for COD of the impact of time delay, the biggest export COD nonlinear prediction function, the optimal stability for the COD concentration in a certain level of concentration adjustment amount for each indicator, conclusion.

Sewage treatment; COD; Principal component analysis; Time series analysis; Nonlinear prediction; SQPM nonlinear constraints

2016-01-14.

国家自然科学基金(11301001)；安徽省创新创业项目(AH201410378258).

葛福婷(1995-)，女，安徽舒城人，安徽财经大学统计与应用数学学院硕士研究生,研究方向：经济统计.

朱家明(1973-),男,安徽泗县人, 硕士,安徽财经大学副教授,数学建模实验室主任,研究方向:应用数学与数学建模.

X523

A

1673-8462(2016)02-0056-07