衣、食、住、行与数学

☉山东省济宁市第十四中学姚俊锁

衣、食、住、行与数学

☉山东省济宁市第十四中学姚俊锁

随着社会的多元化发展，数学的应用愈加广泛，从近几年的中考中可窥见一斑.数学生活化是新课程的一大特点，我们的“衣、食、住、行”都潜藏着数学，同时也昭示出数学的无处不在，与我们的生活息息相关.

一、“衣”与数学

俗话说：“穿衣戴帽，各自一套.”殊料其中也有学问，若能静下心来，探究一番，将别有一翻趣味.

例1（2009年白银市）鞋子的“鞋码”和鞋长（cm）存在一种换算关系，下表是几组“鞋码”与鞋长换算的对应数值：（注：“鞋码”是表示鞋子大小的一种号码）

鞋长16 19 21 24鞋码22 28 32 38

（1）设鞋长为x，“鞋码”为y，试判断点（x，y）在你学过的哪种函数的图像上？

（2）求x、y之间的函数关系式；

（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少？

评析：鞋子竟然与函数搭上钩，真让人殊料不及，本来“冰冷”的函数，一下子提升了温度，无形中驱动了考生探索的积极心向.（1）需要在观察的基础上，用数学进行分析，才能作出是什么函数的判断，是对初中三类函数的大盘点；（2）用待定系数法求解析式；（3）利用解析式实现数学与生活的转换.

答案：（1）一次函数.

（3）y=44时，x=27，即此人的鞋长为27cm.

例2（2015年绍兴市）由于木质衣架没有柔性，在挂置衣服的时候不太方便操作.小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可.如图1，衣架杆OA=OB=18cm，若衣架收拢时，∠AOB=60°，如图2，则此时A、B两点之间的距离是______cm.

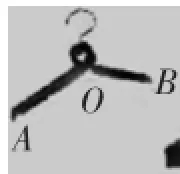
图1

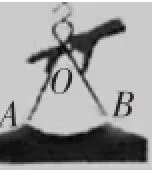
图2

评析：“衣架”以本身的体态与等边三角形拿捏在一起，成为考查等边三角形的有效载体.其关键是根据有一个角是60°的等腰三角形推知为等边三角形，然后获得答案.

答案：18.

二、“食”与数学

俗话说：“人是铁，饭是钢，一顿不吃饿得慌.”日常饮食中也不乏数学的影子，只要我们留意生活，学会用数学的眼光看待身边的生活，那么生活中将处处透射着数学的光辉.

例3（2006年台州市）小敏中午放学回家自己煮面条吃，有下面几道工序：①洗锅盛水2分钟；②洗菜3分钟；③准备面条及佐料2分钟；④用锅把水烧开7分钟；⑤用烧开的水煮面条和菜要3分钟.以上各道工序，除④外，一次只能进行一道工序.小敏要将面条煮好，最少用_____分钟.

评析：本题以统筹学知识为背景，考查学生的数学素养和灵活运用知识的能力，同时能让学生了解数学的多样性及其应用的广泛性.

答案：12分钟.

例4（2015年菏泽市）列方程（组）或不等式（组）解应用题：2015年的5月20日是第15个中国学生营养日，我市某校社会实践小组在这天开展活动，调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息（如下表）.

信息1.快餐成分：蛋白质、脂肪、碳水化合物和其他. 2.快餐总质量为400克. 3.碳水化合物质量是蛋白质质量的4倍.

若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%，求这份快餐最多含有多少克的蛋白质？

评析：本题通过信息表展现了快餐的各种成分，并把相关数据嵌入，这样一来方程模型、不等式就出现了，如下考查模型思想，活泼灵动，情趣十足，有助于学生情感的投入和成绩的发挥.

答案：56克.

三、“住”与数学

随着生活水平的不断提高，当下的家庭购房呈现出自主选择与决策的态势，更加关注住房周围的环境，楼内公共设施的情况，以及室内的相关配置等，都进入了人们的选择空间；另外，在中考试题中也不乏有关“住”的设施等背景的题目，如折叠床、折叠椅等.

例5（2006年苏州市）今年，苏州市政府的一项实事工程就是由政府投入1000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作，对社区内1200户家庭中的120户进行了随机抽样调查，并汇总成下表：

改造情况改造水龙头改造马桶1个2个3个4个1个2个户数20 31 28 21 12 69 2均不改造

（1）试估计该社区需要对水龙头、马桶进行改造的家庭共有＿____＿户.

（2）改造后，一只水龙头一年大约可节省5吨水，一只马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨自来水？

（3）在抽样的120户家庭中，既要改造水龙头又要改造马桶的家庭共有多少户？

评析：本题以表格的形式展示信息，充分利用样本估计总体的思想，进行计算，并将方程的考查融入其中，使统计知识的考查有了新的依托，拓宽了命题的领域，为考生的公平竞争提供了平台.

答案：（1）1000.

（3）设既要改造水龙头又要改造马桶的家庭共有x户，则只改造水龙头不改造马桶的家庭共有（92-x）户，只改造马桶不改造水龙头的家庭共有（71-x）户，列方程x+（92-x）+（71-x）=100，解得x=63（户）.

例6（2015年金华市）图3是一张可以折叠的小床展开后支撑起来放在地面的示意图，此时，点A、B、C在同一直线上，且∠ACD=90°.图4是小床支撑脚CD折叠的示意图，在折叠过程中，△ACD变形为四边形ABC′D′，最后折叠形成一条线段BD″.

（1）小床这样设计应用的数学原理是______；

（2）若AB∶BC=1∶4，则tan∠CAD的值是______.

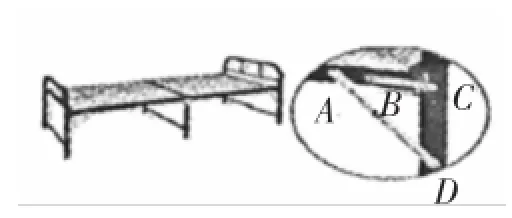
图3

图4

评析：本题以可变的折叠床为背景，贴近学生生活，为学生所喜闻乐见，就在这折折叠叠中，几何图形的重要性质融入其中，有效地考查了学生的知识变通能力.

（1）在折叠过程中，由稳定的△ACD变形为不稳定四边形ABC′D′，最后折叠形成一条线段BD″，小床这样设计应用的数学原理是：三角形的稳定性和四边形的不稳定性.

（2）因为AB∶BC=1∶4，故设AB=x，CD=y，则BC=4x，AC=5x.由旋转的性质知BC″=BC=4x，AC″=3x，C″D″=y，所以AD=AD″=AC″+C″D″=3x+y.

在Rt△ACD中，根据勾股定理得AD2=AC2+CD2，即所以

例7（2015年淄博市）如图5是一把折叠椅子，图6是椅子完全打开支稳后的侧面示意图，其中AD和BC表示两根较粗的钢管，EG表示座板平面，EG和BC相交于点F，MN表示地面所在的直线，EG∥MN，EG距MN的高度为42cm，AB=43cm，CF=42cm，∠DBA=60°，∠DAB= 80°.求两根较粗钢管AD和BC的长.（结果精确到0.1cm.参考数据：sin80°≈0.98，cos80°≈0.17，tan80°≈5.67，sin60°≈0.87，cos60°≈0.5，tan60°≈1.73）

图5

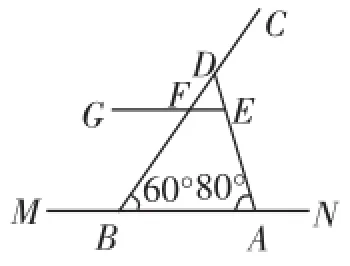
图6

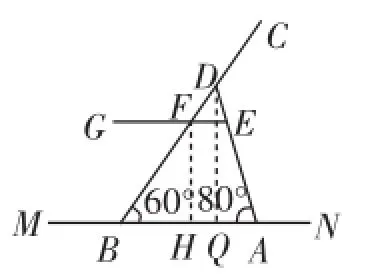
图7

评析：本题与例6可谓呼应之题，一个折叠床、一个折叠椅，通过这些基于学生生活的背景考查了直角三角形的应用：画出平面图形，构造出直角三角形转化为解直角三角形问题.根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形.作FH⊥AB于H，DQ⊥AB于Q，如图7，FH=42cm，先在Rt△BFH中，利用∠FBH的正弦计算出BF≈48.28，则BC=BF+CF≈90.3（cm），再分别在Rt△BDQ和Rt△ADQ中，利用正切定义用DQ表示出BQ和AQ，得，则利用BQ+AQ= AB=43得到，解得DQ≈56.999，然后在Rt△ADQ中，利用sin∠DAQ的正弦可求出AD的长.

答案：两根较粗钢管AD和BC的长分别为58.2cm、90.3cm.

例8（2015年台州市）如图8，这是一把可调节座椅的侧面示意图，已知头枕上的点A到调节器点O处的距离为80cm，AO与地面垂直，现调整靠背，把OA绕点O旋转35°到OA′处，求调整后点A′比调整前点A的高度降低了多少？（结果取整数）？（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）

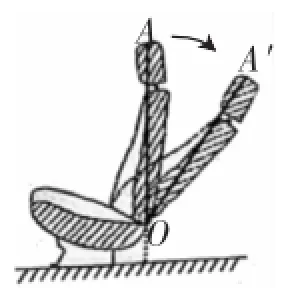
图8

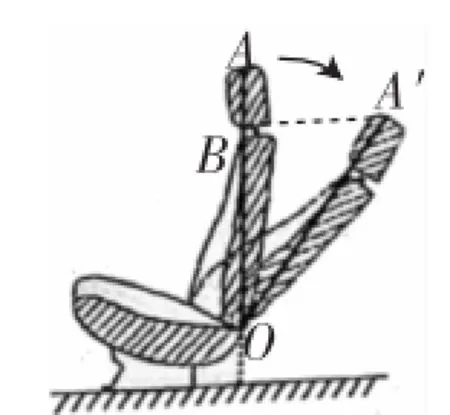
图9

评析：借力可调节座椅的可动设置问题，在自然的生活中与数学对接，充分体现了数学源于生活又作用于生活的理念.如图9，作A′B⊥AO于B，根据题意OA=OA′= 80cm，∠AOA′=35°，所以OB=OA′·cos35°=80×0.82≈65.6cm，所以AB=OA-OB=80-65.6≈14cm.

答案：调整后点A′比调整前点A的高度降低了14cm.

四、“行”与数学

随着人们生活水平的日益提高，生活观念在悄悄地发生改变，“低碳生活”理念已渐入人心，原本心仪的小轿车代步出行，正逐步被自行车所取代，人们更加关注绿色生活，健康生活，除室外自行车锻炼外，跑步机等也走进了千家万户，以此命制的考题已见诸于中考.

例9（2014年泰州市）图10、图11分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1.6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0.8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0.1m）.（参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）

图10

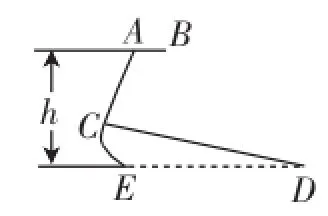
图11

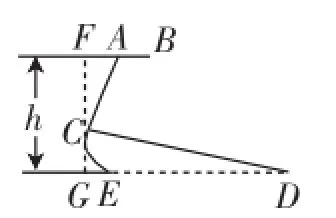
图12

评析：此题以跑步机为几何原形，把解直角三角形的应用融入，考查了三角函数的基本概念及运算，其关键是调用数学知识解决实际问题.如图12，过C点作FG⊥AB于点F，交DE于点G.在Rt△ACF中，根据三角函数可求CF，在Rt△CDG中，根据三角函数可求CG，再根据FG= FC+CG即可求解.

答案：跑步机手柄的一端A的高度约为1.1m.

例10（2014年白银市）为倡导“低碳生活”，人们常选择以自行车作为代步工具，图13所示的是一辆自行车的实物图.图14是这辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45cm和60cm，且它们互相垂直，座杆CE的长为20cm.点A、C、E在同一条只显示，且∠CAB=75°.（参考数据：sin75°≈0.966，cos75°≈0.259，tan75°≈3.732）

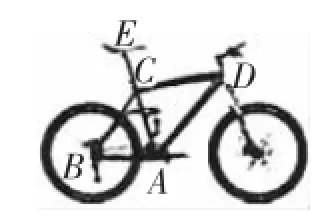
图13

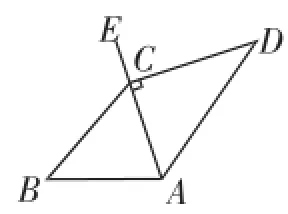
图14

图15

（1）求车架档AD的长；

（2）求车座点E到车架档AB的距离（结果精确到1cm）.

评析：此题从自行车架构中抽取了部分几何示意图，能让考生触摸到数学的温情.通过辅助线的构建考查了勾股定理与三角函数的应用.（1）在Rt△ACD中利用勾股定理求AD即可.（2）如图15，过点E作EF⊥AB，在Rt△EFA中，利用三角函数求EF=AE·sin75°即可.

答案：（1）AD的长是75cm；（2）车座点E到车架档AB的距离约是63cm.

“处处留心皆学问”，我们学会用数学的眼光看生活，数学的影子将无处不在，善于发现并总结生活数学的规律，定会让我们智慧过人，受益终生！