一次函数应用题的教学手记与命题思考

☉江苏省苏州工业园区青剑湖学校石亚军

一次函数应用题的教学手记与命题思考

☉江苏省苏州工业园区青剑湖学校石亚军

近期教学一次函数，几本练习册上大量引用各地所谓的中考原题，由于中考原题在全卷中承载着很多考查功能，所以将有些中考题简单下放到新授期间来直接练习有时并不恰当.近期我们教学过程中遇到两道较为流行的中考一次函数应用题，教与学过程中引发一些思考，本文先简述这两道试题的思路，并对相关考题给出商榷与变式改编，提供研讨.

一、两道一次函数应用题的教学记录

考题1（2014年黑龙江绥化中考第23题）在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车、乙骑电动车沿公路匀速驶向C村，最终到达C村.设甲、乙两人到C村的距离y1、y2（km）与行驶时间x（h）之间的函数关系如图1所示，请回答下列问题.

（1）A、C两村间的距离为________km，a＝________；

（2）求出图中点P的坐标，并解释该点坐标所表示的实际意义；

（3）乙在行驶过程中，何时距甲10km？

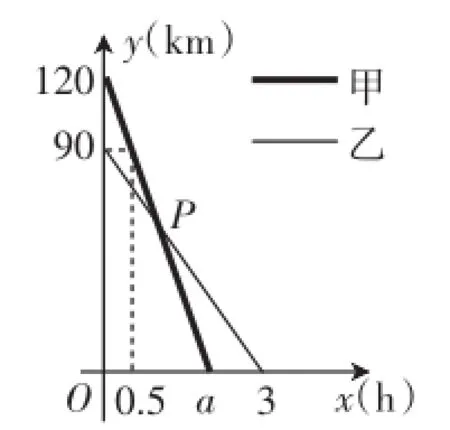
图1

思路简述与教学困惑：前两问没有什么争议，答案分别是：（1）120，2（.2）两人经过1小时相遇，且距离C村为60km.但是第（3）问有学生给出两个情况，即乙在行驶（h）或（h）时与甲相距10km，有学生认为还应该考虑（h）与甲相距10km的情况，即当甲到达目的地后乙还在行程中，这时也可能与甲相距10km.有些学生认为，甲到达乙地后，会有很多可以想象的情况，比如乙村庄是一个多大的范围？甲到达乙村后就留在原地静止不动吗？面对这些疑问和想象，确实教者无法回答，不知当初预设这道考题的命题组专家是否预见到这类“想象”与可能的思考呢？反正笔者面对学生这样的质疑，只能是如同“两小儿辨日”一样，无法应答.

考题2（2015年浙江丽水市某校初二期末模考题）某电视台摄制组乘船往返于A、B两个码头，在A、B间设立拍摄中心C，拍摄景色.往返过程中，船在C、B处均不停留，离开码头A的距离s（km）与航行的时间t（h）之间的函数关系如图2所示.根据图像提供的信息，解答下列问题.

（1）船从码头A→B，航行的时间为______h、航行的速度为______km/h；船从码头B→A，航行的时间为______h、航行的速度为______km/h.

（2）若拍摄中心C设在离A码头25km处，摄制组在拍摄中心C分两组行动，一组乘橡皮艇漂流而下，另一组乘船到达码头B后，立即返回.

①求船往返C、B两处所用的时间；

②两组在途中相遇，相遇时船离拍摄中心C的距离为______km.

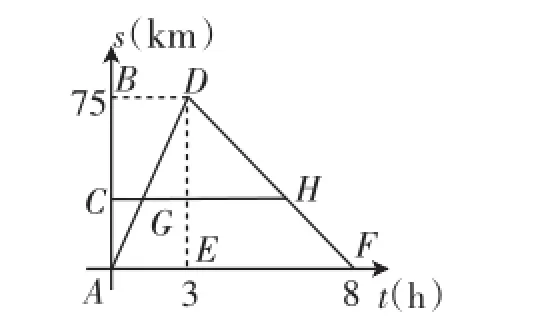
图2

思路简述与教学困惑：第（1）问并不复杂，大多数学生都能顺利解答.但是第（1）问掩盖着问题生活背景之后的一些隐含条件：船在静水中的速度是20km/h，水流速度是5km/h.而这些隐含条件在后续问题的探究中将成为重要起点.

比如，笔者曾使用如图3所示的PPT，通过渐次呈现的动画功能出现各个必要的辅助思想的信息，但效果还是很明显，包括一些数学优秀的学生仍然认为橡皮艇漂流的速度为什么是一定是5km/h？少数学生在外出旅游时曾参加过一些漂流项目，知道漂流往往是游船在人力划桨或撑篙情况下的一种漂流项目，这也导致学生理解漂流的情境出现障碍.

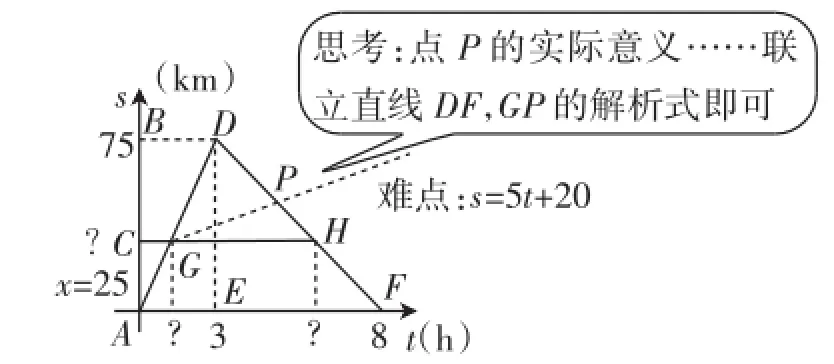
图3

后来，为了追求更多的学生能理解难点，笔者又重新构思了如图4这样的简化图形，也就是在图3的基础上，设点G处为原点，重新设出横轴、纵轴，船只行驶离开拍摄中心C的距离s（km）与航行的时间t（h）的函数图像，如图4，这样过点G的射线（正比例函数s=5t）可视为漂流的橡皮艇的图像.

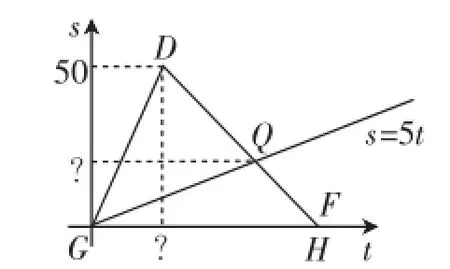
图4

经过前后两次解读、展示不同的思考，不少学生表示理解了，并且他们认为难点不是图像的理解，而是纠结橡皮艇的速度与水流速度之间没有对应上去.

二、函数应用问题的命题与教学思考

众所周知，数学来源于生活，服务于生活.然而如何源于生活，恐怕没有多少人能说得清，连那么多的数学家在相关著作中，对人类更早期的不同民族的数学探究也没有精确的描述，缺少必要的史料佐证.再说数学服务于生活，如何服务生活、贴近生活呢？不同的数学家也有不同的表述，再从数学的后续发展来看，作为应用方向会产生很多数学分支.所以，初中阶段对函数的应用问题的命题与教学，笔者提出如下思考.

1.问题背景追求简洁好懂，杜绝歧义理解

当前有些地区对应用问题的考查常常追求贴近本地区生活实际，从报刊、新闻中摘引大段的生活背景，考查学生从繁杂生活背景中解读出数学信息，并选取相应的数学工具来解决问题，这样的考查目的对于考查数学建模思想有一定的好处，是其积极的一面.然而对于目前中考高利害的现实背景之下，这样的大容量的阅读问题也是值得商榷的，因为学生除了这类应用问题要投入较多的时间成本答题，还有很多题量的考题需要思考，这对于惜时如金的考场上来说，在阅读量方面做出过多、过高的要求，我们认为值得商榷.从上文中“考题2”来看，熟悉近十年考题的同行应该知道，“考题2”相对于浙江丽水中考原题来说，已“瘦身”不少，然而阅读量还是很大，且有理解上的障碍与歧义，或者与部分学生生活经验冲突，使得考题的内容效度不高.对比来看，国际上大学生历年都会有所谓的数学建模大赛，往往一道生活问题，给大学生团队（5人左右）一周的时间提交解决方案.这样来看，考题中的生活问题的命题需要十分慎重，“结构不良”的试题慎用.

2.钻研教材应用问题表述，倡导变式改编

对于应用问题的考查，我们认为认真钻研教材上的应用问题的表述，并做适当的变式改编作为各级考试的要求是恰当的.根据教学经验，学生如果能掌握教学上提供的不同类型的应用问题，则他们在函数应用问题的课标要求也基本达到了.笔者常常见到不少应用问题的考查在结合本地区生活情境的同时，也离开了教材上的规范、恰当的表述和呈现，使得问题的呈现出现背景不公平，不同考生理解偏差现象.这些结构不良的应用问题作为课题学习，可以在平时教学活动开展讨论对话，但作为试题考查，需要谨慎打磨.

3.引导学生准确理解情境，防止钻牛角尖

比如“考题1”问题背景取材于教材，然而人为增设了所谓相距10km的考查要求，本意是想考查分类讨论思想，但是却出现一些思考上的分歧.一方面命题组要尽可能避免这类理解上的分歧，另一方面，平时解题教学时，也要注意引导学生准确理解题意，防止钻牛角尖，比如考题2对于漂流的理解，考生不能根据自己旅游时参加的一些个性化漂流项目的体验来对应考题中的理想化的数学问题.

三、命题打磨与改编

作为文末，我们对两道考题给出自己的打磨意见和改编，提供思考：

考题1（改编第3问）：甲在行驶过程中，何时距乙10km？

考题2：（题干不变，节约篇幅，只给出变式问题）

（1）求图2中线段DF对应的函数关系式；

（2）水流速度是多少？

（3）若拍摄中心C设在离A码头25km处，摄制组在拍摄中心C分两组行动，一组乘橡皮艇顺着水流速度漂流而下，另一组乘船到达码头B后，立即返回，返回途中遇到乘橡皮艇小组，此时他们离拍摄中心C的距离是多少？

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.【美】波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.H