浅谈中考数学命题的基本方向及其对策
☉江苏省如皋市东陈镇雪岸初级中学陶成龙
浅谈中考数学命题的基本方向及其对策
☉江苏省如皋市东陈镇雪岸初级中学陶成龙
中考数学命题改革是推行课程改革的突破口,是落实新课程理念最有效、最直接的途径之一.随着基础教育课程改革的逐步深入,以知识立意向能力立意为转变,重视知识的发生、发展过程,突出创新思维成为中考数学命题的新基本方向.笔者在认真研读《全日制义务教育数学课程标准(实验稿)》的基础上,搜集整理并细致研究了近几年江苏十三大市中考命题新趋势和新要求,发现每年中考数学命题在某种程度上均体现了数学课程标准所要求的义务教育阶段要促成“学生都能获得良好的数学教育,不同的学生在数学上得到不同的发展”的总体要求.试题虽在不断推陈出新,但呈现出以下相对稳定的特征.
一、试题的设计在重点考查“双基”的基础上,更多地关注对学生数学思想与方法的考查
数学课程的总体目标被细化为四个方面:知识与技能,数学思考,解决问题,情感态度.由此可见,基础知识、基本技能仍然是学生学习的重点,这是现代公民具备数学素养的必备要求.因此,对“双基”内容的考查仍然是课改中考命题的重点.但是笔者注意到,这几年各市中考数学试卷在着重考查学生静态显性数学知识的同时,开始重点关注对学生动态隐性数学知识的考查,即加大对运用数学思想与方法解决问题的考查力度.以数学核心知识、核心思想方法为载体设置中考试题,显然已成为中考命题的基本原则.
例1(南通中考试题)如图1,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为_____.

图1
教学对策:例1将基础知识、基本技能与数学思想的考查自然地融合在一起.这道题目对于绝大部分同学而言并不困难,部分同学通过待定系数法求出k和b的值,从而求出不等式组的解集;而有的同学利用数形结合的思想直接观察出不等式组的解集,显然体现出了两种不同的数学能力素养.“知识是数学的躯体,问题是数学的心脏,数学思想是数学的灵魂”.因此,作为一名数学教育者,除了向学生传授知识与技能,更应注重数学思想与方法的感悟性教学.这就要求在课堂教学中:(1)要加强新旧知识的联系与区别,善于抓住在概念的形成过程和结论的推导过程中向学生渗透数学思想和方法的机会;(2)在指导学生解题过程中,除了注重解题思路的探索过程,还要关注让学生养成解题后反思与领悟的习惯,即要善于总结凝练出解题方法和规律,形成通性通法;(3)善于多让学生经历自主探究与合作交流的过程,养成善于倾听和乐于分享的习惯.总之,只有将抽象的数学思想与数学知识有机地融合在一起教学,让学生切身体验到数学思想与方法对于解决问题的独特魅力,学生才会在很大程度上灵活运用数学思想与方法解决问题,才会把握数学问题的本质.
二、试题的设计更多地关注对学生“数学化”能力的考查
义务教育阶段的数学教育是一种公民教育,其教育目标不是让每位学生成为数学家,而是培养成一位能够以数学角度观察世界,并用数学思维思考与解决现实问题的“数学人”.《标准》指出:数学教学要让学生经历数学化的过程.所谓“数学化”,是指学生能从数学认知水平出发,从数学角度运用数学知识解释事物现象,解决实际问题.因此,各市中考试卷开始出现了一类旨在考查学生“数学化”能力的试题.
例2(镇江中考题)某海域有A、B两个港口,B港口在A港口的北偏西30°的方向上,距A港口60海里.有一艘船从A港口出发,沿东北方向行驶一段距离后,到达B港口南偏东75°方向的C处.求该船与B港口之间的距离即CB的长(结果保留根号).
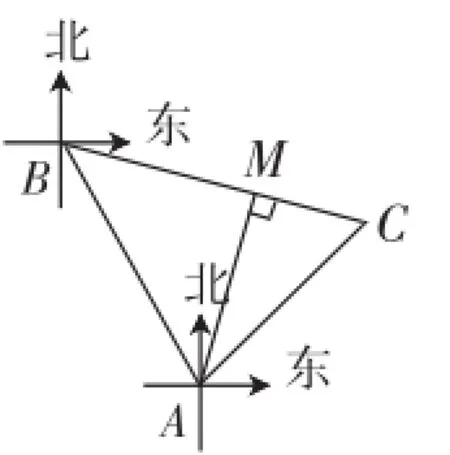
图2
教学对策:例2主要考查学生从解直角三角形角度解决航海当中涉及的方向角、航程等问题.这就要求学生能将现实中的实际问题转化为数学问题.可是“数学化”能力的培养不是一朝一夕就能完成的,而是要具体落实到日常教学点滴之中.因此,在数学教学中要注意:(1)引导学生发现身边的数学问题,充分挖掘现实的、有意义的素材,并提出富有挑战性的数学问题,让学生经历“现实问题—建立模型—解决应用”过程,鼓励学生多从数学角度观察客观世界,多以数学语言描述事物现象,多用数学思维分析现实问题,逐步提高学生的数学化能力;(2)加强数学学科与自然学科、社会学科的综合联系,新教材特别设置了“阅读与思考”和“数学活动”两个栏目,其间介绍了数学在美术、建筑、物理中的应用,”千万不能忽略作为选学内容的教学,而是要多留时间与空间让其阅读与思考,积极开展数学实践活动.因此,只有让学生意识到数学源于生活,又应用于生活,“数学化”能力才会得到进一步提高.
三、试题的设计更多地关注对学生自学能力的考查
《标准》指出:“自主探索与合作交流”是学生学习数学的重要方式.这就要求数学教育不再是老师主动讲,学生被动听的陈旧模式,而是变革为教师参与指导,学生自主建构的新模式.为了落实课改精神,近年中考数学试卷出现了一类旨在考查学生自学能力的阅读理解题.
例3(扬州中考题)阅读下面材料,回答问题:平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:┌P┘,即┌P┘=|x|+|y|(其中的“+”是四则运算中的加法).
(3)求满足条件┌N┘=3的所有点N围成的图形的面积.
教学对策:这类题主要考查学生通否通过经历观察、分析、比较、推理等一系列数学思维活动过程,运用所学数学知识自主解决问题.因此,在数学教学中要注意:(1)加强学习方法的指导,不但“授之以鱼”,更要“授之以渔”,不仅要让学生学会数学知识,而且要让学生学会学习,促其学力的提升,从而具备自主探索新问题的基本数学素养;(2)在学生原有认知基础上,能通过自主探索,建构新知的,教师应予以足够的时间与空间,让其经历知识发生、生成和应用的过程.比如:有理数的加减运算法则,幂的运算性质,方程(组)的解法探究,勾股定理的发现与证明等数学知识,都可以让学生自主探索,教师只要充当好组织管理者、疑点解释者的角色.只要教师少一点儿“讲”,学生多一点儿“悟”,学生的自学能力就会不断地发展.
四、试题的设计更多地关注对学生数学创新能力的考查
发展创新精神是课程改革的一个重要目标.创新精神的一个基本要素是思维活动的独特性与非模仿性,而我们的传统数学教育是以知识积累为目标的,教师仅限于讲授知识,学生只限于模仿,机械式地接受知识.显然,传统数学教育不利于学生创新能力的培养.因此,如何培养学生的创新思维能力成为摆在教育工作者面前的一个难题.各市在课改中中考命题方向上也正在作出相应调整.近年来,出现了一类方案设计型试题.
例4(南京中考题)如图3,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
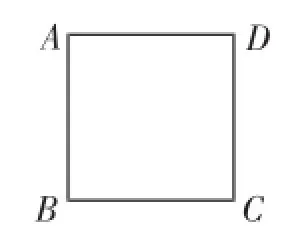
图3
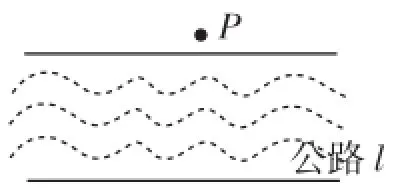
图4
例5(南通中考备用题)如图4,河边有一条笔直的公路l,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸点P到公路的距离,请你设计一个测量方案(测量工具:测角器、尺子).要求:(1)画出测量的示意图,写出测量的步骤;(2)用字母表示测得的数据,求出点P到公路的距离.
教学对策:这不是简单的作图问题,它需要学生具备较强的创造思维能力和丰富的想象力.如何在课堂教学中发展学生的创新思维能力,笔者认为:(1)教师要注意引导学生去发现和提出各种数学问题,伟入爱因斯坦曾经说:“提出一个问题往往比解决一个问题更重要,只有善于发现问题和提出问题的人,才能产生创新的冲动”;(2)编拟一些开放性问题、探索性问题,对学生进行思维训练,激活他们的思维,促其思维开放;(3)营造平等、民主的宽松课堂氛围,对于每个问题的研究要多让学生从多角度、多方位、多途径解决问题,鼓励学生畅所欲言,大胆提出自己的方案,从而让学生形成标新立异、不拘一格的思维特性.
随着课程改革的逐渐深入,课改中考也将会进一步落实课改新精神.因此,准确把握数学课程改革的新理念,研究课改中考数学命题新方向,将会推动教师实施数学教学的新策略,从而提高数学教学水平.Z

