高考试题的开放性和探究性赏析
邓 兴
(贵州师范大学附属中学 贵州 贵阳 550001)
高考试题的开放性和探究性赏析
邓 兴
(贵州师范大学附属中学贵州 贵阳550001)
新课标(实验版)对能力考查与原考纲的最显著变化特点是,提出了高考对学生发现问题、提出问题等探究能力的考查渗透在理解能力、推理能力、分析综合能力、应用数学处理物理问题的能力、实验能力5个方面的能力中考查.这不仅对新课标教学中积极推进探究性教学的肯定,同时探究性教学的内涵、有效性目标更加具体,这对中学物理教学有着积极重要的引领作用.同时,应注意到近几年高考试题的开放性和探究性.下面我们通过几个试题来进行赏析.
【例1】(2011高考新课标全国卷第23题)利用图1所示的装置可测量滑块在斜面上运动的加速度.一斜面上安装有两个光电门,其中光电门乙固定在斜面上靠近底端处,光电门甲的位置可移动,当一带有遮光片的滑块自斜面上滑下时,与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间t .改变光电门甲的位置进行多次测量,每次都使滑块从同一点由静止开始下滑,并用米尺测量甲、乙之间的距离s,记下相应的t值;所得数据如表1所示.
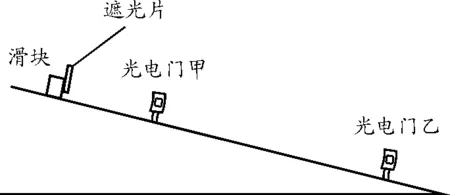
图1
表1实验测得数据
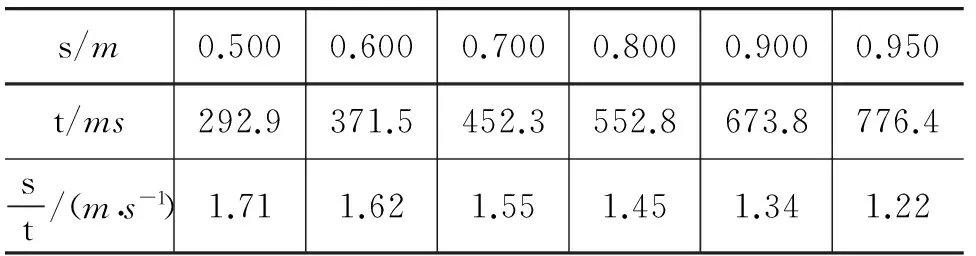
s/m0.5000.6000.7000.8000.9000.950t/ms292.9371.5452.3552.8673.8776.4st/(m·s-1)1.711.621.551.451.341.22
完成下列填空和作图:
(1)若滑块所受摩擦力为一常量,滑块加速度的大小a,滑块经过光电门乙时的瞬时速度v1测量值s和t 4个物理量之间所满足的关系式是________;
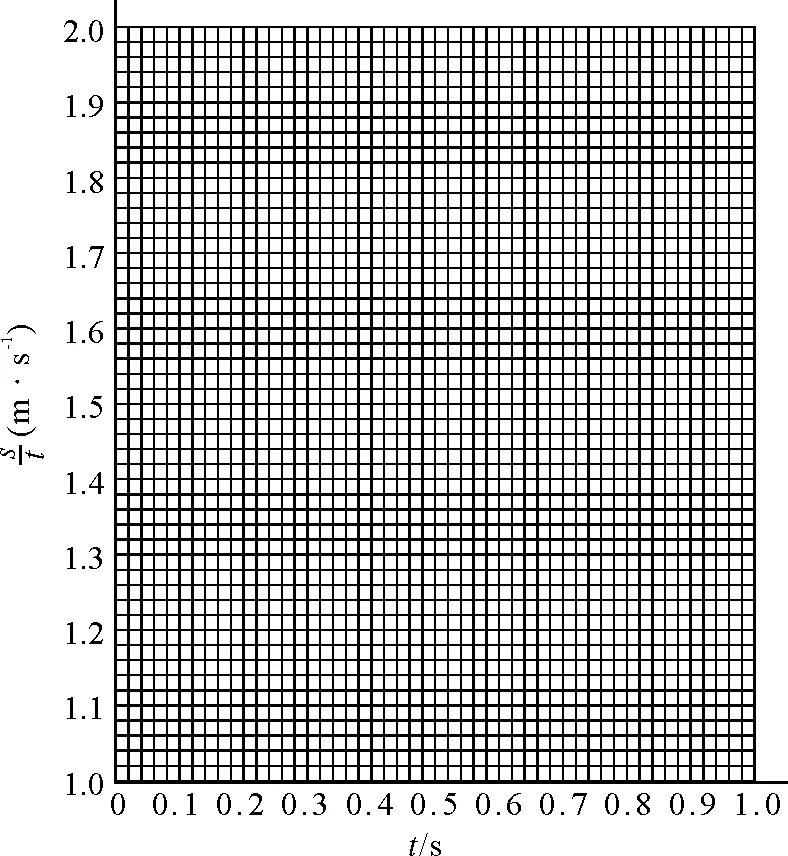
图2
读题获取信息:滑块沿斜面向下做匀加速下滑,通过光电门甲的初速在变,通过光电门乙的末速不变,求:
(1)s,vt,t,a 4个量的关系.我们在高一教材探究、学习、获取的匀变速直线运动规律
vt=v0+at
据此学生能否、或教师能否引导学生在探究中学会探究,主动思考在上述规律中涉及v0,vt,a,t,s 5个量,每个公式只含4个量,能否任意知道了3个量均能求解待求量?应有几个表达式?排列、组合,应有5个表达式,推理得出另外两个表达式
(2)根据列表数据描点作图(坐标比列数据已给定),仅考查基本技能和严谨的科学态度.
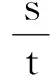
变形得到
本题的探究过程渗透了理解、推理、归纳综合、运用数学工具解决物理问题能力的考查,也渗透了对教学过程的开放性和探究性要求.
【例2】(2011年高考全国新课标理综卷选择题第19题)卫星电话信号需要通地球同步卫星传送.如果你与同学在地面上用卫星电话通话,则从你发出信号至对方接收到信号所需最短时间最接近于(可能用到的数据:月球绕地球运动的轨道半径约为3.8×105m、地球半径为6 400×103m)
A.0.1sB.0.25s
C.0.5sD.1s
解法一:这是一道估算题,令同步卫星离地高度为h
式(1)、(2)联立得
代入数据
T=24×3 600s
g≈π2
R=6 400×103m
得
h≈3.6×107m
选项B正确.
解法二:根据开普勒第三定律
代入数据
T月=27天
T地=1天
r月=3.8×108m
R地=6.4×106m
计算得
h≈3.56×107m
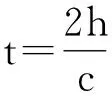
【例3】(2015年高考全国新课标理综卷选择题第16题) 由于卫星的发射场不在赤道上,同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道.当卫星在转移轨道上飞经赤道上空时,发动机点火,给卫星一附加速度,使卫星沿同步轨道运行.已知同步卫星的环绕速度约为3.1×103m/s,某次发射卫星飞经赤道上空时的速度为1.55×103m/s,此时卫星的高度与轨的高度相同,转移轨道和同步轨道的夹角为30°,如图所示发动机给卫星的附加速度的方向和大小约为
A. 西偏北方向,1.9×103m/s
B. 东偏南方向,1.9×103m/s
C. 西偏北方向,2.7×103m/s
D. 东偏南方向,2.7×103m/s
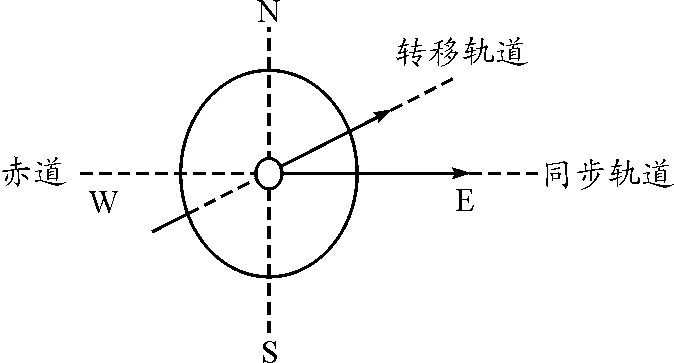
图3
通常的解答是:根据题目信息可知:卫星在转移轨道上的速度v1=1.552×103m/s(从题可知方向为北偏东30°方向)和待求发动机给卫星的附加速度v2是分速度,而同步卫星环绕速度v=3.1×103m/s是合速度,方向向东.而v1和v之间的夹角为30°.利用余弦定理可知,所需附加速度v2的大小为
根据题目的条件,经估算可得东偏南方向,选项B正确.
通常对本题的评析是:本题通过同步卫星发射后需要从转移轨道经过调整后再进入同步轨道的实际问题,考查了学生的理解能力和简单计算能力.试题取材紧密联系航天科技发展,涉及卫星变轨这一重大技术问题,考查内容涉及运动的合成等知识点.然而,我们更应该看到,新课程标准从力的合成实验探究到教材的习题要求对矢量合成用作图法求解已经有了明确的能力要求,加之题目给定的关键词“约为”,利用试题图像作矢量合成图便可直观得出(毋须计算)选项B正确.即使直观性较差的学生也可用刻度尺量出矢线长进行估算,得出结果,十分简捷.事实上,笔者专门做过调查,利用余弦定理进行估算的学生,最快也需5min才能得出结果,这必然导致理综解答时间不够.
以上3例十分明确地告诉我们学生探究能力是在日常教学的探究活动中潜移默化、逐步提高的;所组织的探究活动是否具有实效就在于学生能否积极主动参与,能否促进能力提升.探究能力是我们日常教学的自然生成,我们必须脚踏实地在日常探究式教学活动中注意实效性,没有捷径可循.
2016-07-05)

