具有小世界邻域结构的教与学优化算法*
王培崇,马 玥,耿明月,汪慎文
1.河北地质大学 信息工程学院,石家庄 0500312.中国矿业大学 信息与机电学院,北京 1000833.重庆邮电大学 计算机学院,重庆 400065
具有小世界邻域结构的教与学优化算法*
王培崇1,2+,马玥1,耿明月3,汪慎文1
1.河北地质大学 信息工程学院,石家庄 050031
2.中国矿业大学 信息与机电学院,北京 100083
3.重庆邮电大学 计算机学院,重庆 400065
教与学优化(teaching-learning-based optimization,TLBO)算法是近年来提出的一种通过模拟“教”与“学”行为的群体智能算法。为了克服教与学优化算法容易早熟,解精度较低,后期收敛速度慢等弱点,提出了一种改进的教与学优化算法,并命名为S-TLBO(small world neighborhood TLBO)。该算法采用小世界网络作为其种群的空间结构关系,种群中的个体被看作是网络上的节点。在算法的“教”阶段,学生基于概率向教师个体进行学习,而在“学”阶段,学生则在自己的邻居节点中随机选择较为优秀的个体进行学习。为了提高加强算法的勘探新解和开采能力,引入教师个体执行反向学习算法。在多个经典的测试函数上的实验结果表明,所提出的改进算法具有较高的全局收敛性和解精度,适合于求解较高维度的多模态函数优化问题。
教与学优化(TLBO);小世界网络;邻域结构;反向学习(OBL)
1 引言
Rao提出的教与学优化(teaching-learning-based optimization,TLBO)[1-4]算法是群体智能算法的典型代表之一,该算法的灵感来源于生活中自然班级的教和学行为。通过模拟教师的教学和学生相互之间的学习实现种群的进化。教与学优化算法具有参数少,求解速度较快,设计思想简单,容易实现等特点,受到了众多研究者的关注。
为了提高算法的求解能力,克服该算法在后期收敛速度慢,容易陷入局部最优的问题,文献[4]引入了局部学习和自学习机制,使学生不仅可以向其邻居进行学习,而且还能够进行自学习。Rao等人[5]为了进一步提高算法的求解能力,在TLBO中利用精英个体替换部分劣质解,并删掉了重复的学生个体,该算法被命名为精英教与学优化(elitist TLBO,ETLBO)算法。实验表明该算法具有较快的收敛速度,但是鲁棒性稍差。于坤杰等人[6]在ETLBO算法的基础上进一步提出了精英反馈机制教与学优化算法,每次迭代之后劣质个体向精英个体反馈其本身状态变化情况,并根据变化情况进行修正。仿真实验结果表明,该算法具有较高的精度和鲁棒性。为了使算法的后期种群多样性得以较好地维持,Rajasekhar等人[7]提出了相对精英教与学优化(oppositedelitistTLBO,OETLBO)算法,学生个体不仅仅向教师个体进行学习,还增加了学生个体向相对精英个体的学习,避免了学生个体过早聚集于教师个体周围,从而使算法在后期能够较好保持种群的多样性,但是算法的精度较标准TLBO算法提高较少。文献[8]提出了改进的多教师自适应教学TLBO算法,该算法中允许设置多个教师个体,教师的教学因子被修改为自适应变化,随着迭代次数的变化呈现线性变化。此外,该算法还为学生个体增加了自我学习机制,以加快算法的收敛。但是,该教学因子设置为简单的线性变化,缺少科学性。教与学优化算法已经被应用于诸多领域,并取得了较好的效果,其中主要包括Realistic flow shop rescheduling[4]、数据聚类问题[9]、派送问题中的参数优化[10]、PID控制器优化[11]、二次指派问题[12]等。
相关研究发现,标准TLBO算法存在着诸如解精度较低,容易早熟,后期收敛速度慢等弱点[5]。为了克服算法的这些弱点,改善其求解能力,本文提出了一种引入小世界邻域结构的教与学优化(small world neighborhood TLBO,S-TLBO)算法,个体的邻居基于小世界网络技术定义,学生基于概率机制向教师学习,并向自己的邻居进行学习。
2 标准教与学优化算法
算法1 TLBO算法
不失一般性,以最小化minf(x1,x2,…,xn)问题为研究实例。
输入:种群规模N,最大迭代次数n。
输出:最佳个体Xbest(t)。
步骤1设置算法的相关参数。
步骤2初始迭代次数t=0,并在解空间内随机产生初始种群。
步骤3计算种群中所有个体的适应度,从中选择适应度最优的个体将其设为教师Xtea(t)。
步骤4教师对学生实施教学。
步骤5学生之间进行互相学习。
步骤6算法满足终止条件,输出最佳个体Xbest(t),终止算法;否则,转步骤3。
说明:学生个体通过步骤4、步骤5产生新的子状态,并通过优胜劣汰的方式对自身的状态进行更新。
算法的详细资料请参考文献[1-2]。
3 小世界邻域教与学优化算法
现实生活中,人与人之间通过各种连接构成一个复杂的网络,而邻居往往对个体的学习进化等有较大的影响。借鉴此思想,考虑小世界网络介于随机网络与结构化网络中间,因此将TLBO种群设置为小世界网络结构邻域。
3.1相关定义
因为教与学优化算法中种群内个体之间的学习具有双向性,所以本文采用无向图定义小世界网络。
定义1[13]设图G=(V,E)表示一个小世界网络,其中V={v1,v2,…,v3}为节点集,E={e1,e2,…,en}为边集合。
定义2[13]设存在任意两个节点vi,vj∈V,如果存在
3.2小世界网络构造
在本算法中,个体之间通过相互间的小世界邻域结构进行信息交互,因此在种群初始化过程中首先要构建小世界网络。借助相应的建模方法获得小世界网络。
算法2小世界网络生成算法
输入:n个节点,节点的重联概率p和k=2,迭代次数t。
输出:小世界网络。
步骤1将n个节点中的每一个连接到直接邻居,和邻居的邻居生成一个k-规则网络,该网络的链路数目是m=2n条。
步骤2对于每一个链路,u=1,2,…,m,基于概率p重联链路u。
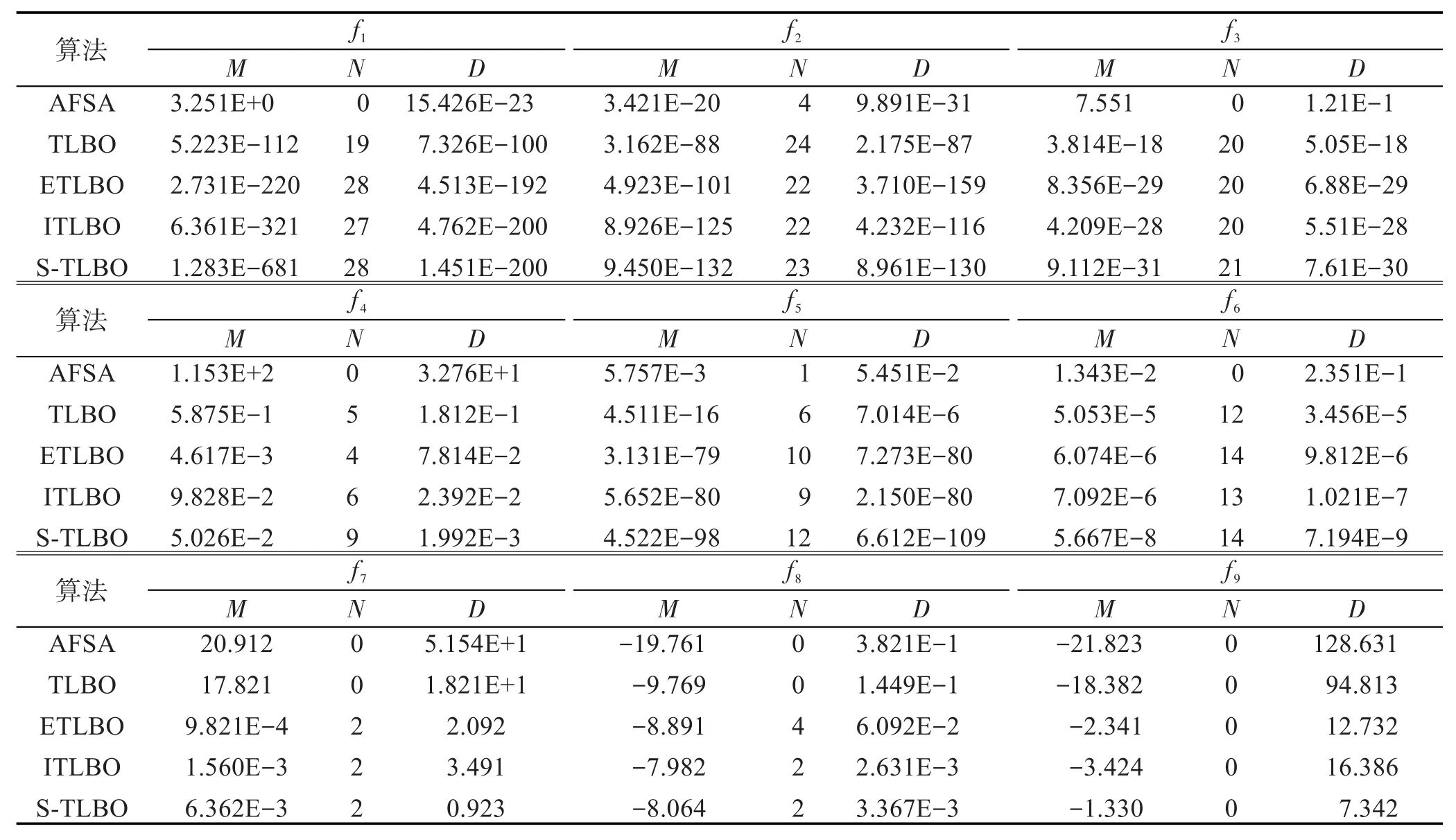
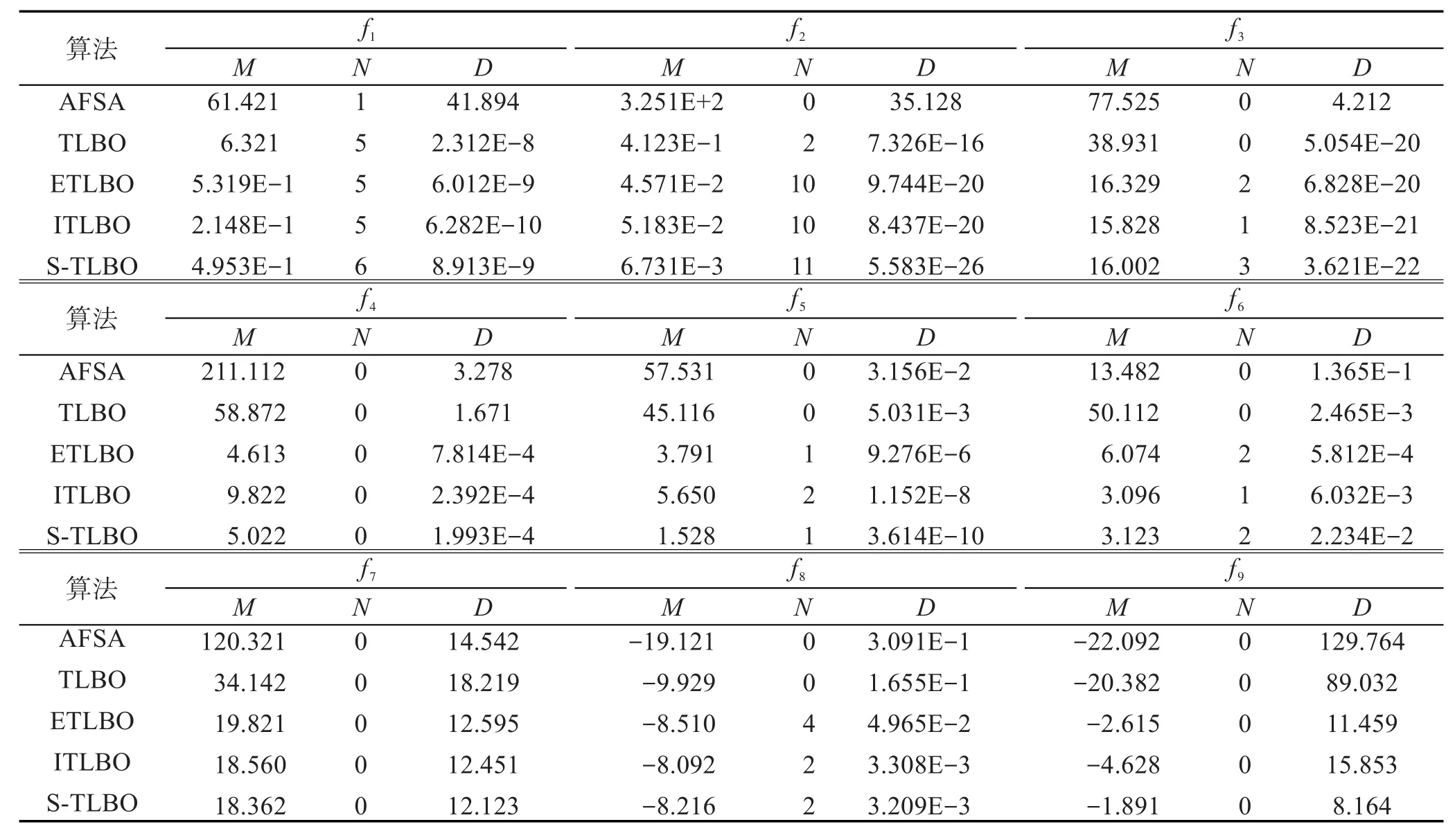
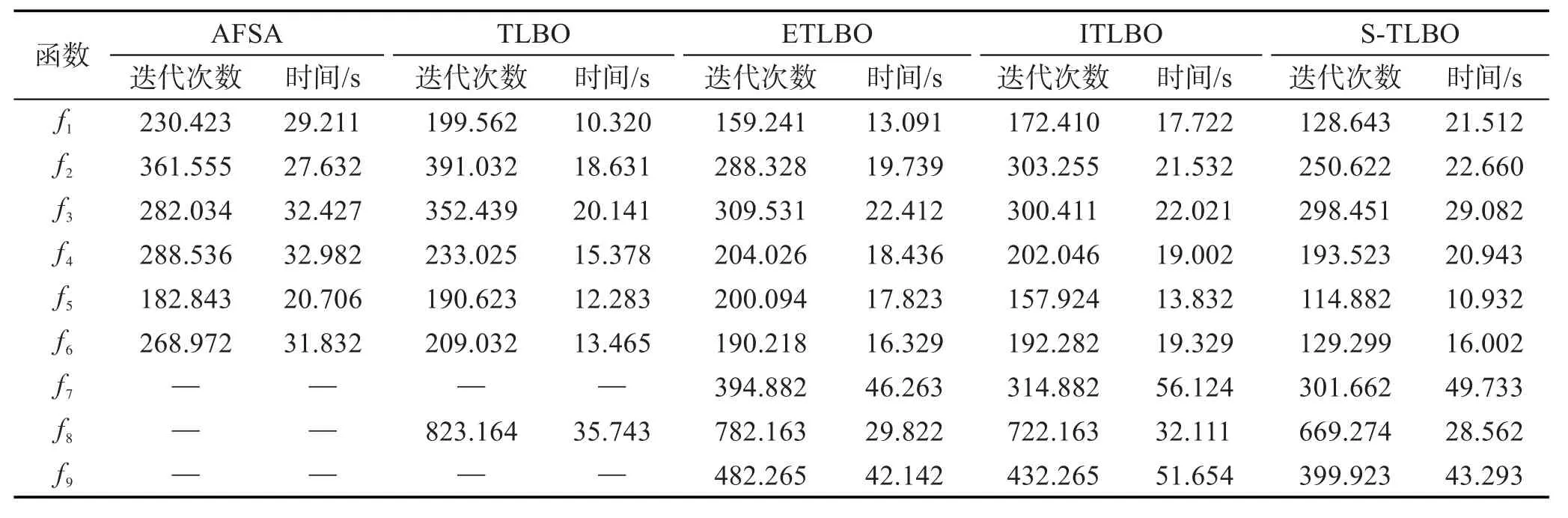
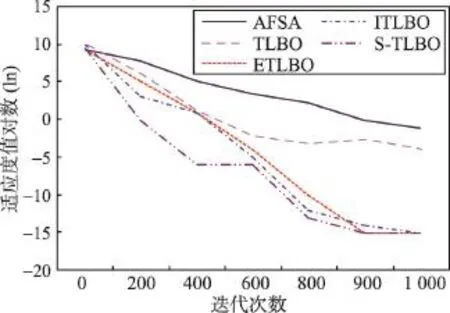
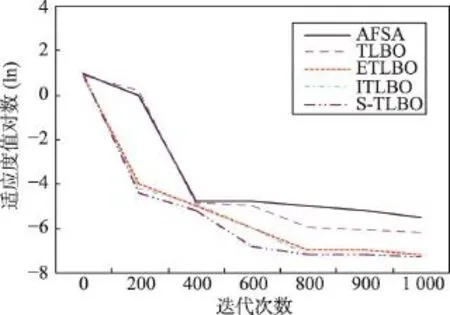
步骤3产生随机数r,如果r 3.3教师“教”行为的改进 TLBO算法中教师为种群的最佳个体,该个体通过其教行为,提高其他个体的状态,以加速算法的收敛。但是在该步骤中,学生个体在被“教”之后,采用优胜劣汰的机制更新自身的状态,往往也容易使种群陷入局部最优。因此修改为学生个体以一定的概率向教师进行学习,概率计算公式为: 式中,f为种群的适应度均值;p0∈(0,1)。从该公式中可以看出,状态越是优秀的个体向教师学习的概率越高,状态越差的个体,向教师学习的概率越低,这样可以使优秀的学生个体协助教师的搜索,而且也能够缓解种群多样性下降的速度。学习公式为: 其中,α=round(1+rand(0,1))是教学因子,round函数为四舍五入,rand()产生指定范围内的随机值。学生向教师学习之后,应用所产生的子状态直接更新学生状态。 3.4小世界邻域下学生的“学”行为 小世界理论认为,网络中的某个节点只需要通过6个节点即可与其他节点发生联系。基于此理论,将学生的“学”行为修改如下: 设Xi(t)为当前个体,其直接邻居集合为N(Xi(t)),Xi(t)则向自己邻居集合内最优的个体进行学习。如果Xi(t)的邻居仅有一个,且是当前教师个体Xtea(t),则从Xtea(t)的邻居中随机选择两个个体,并择优进行学习,依次类推。通过式(3)产生新状态,采用优胜劣汰的方式更新Xi(t): 其中,Xr1(t)为被选出学习的个体。 如果Xi′(t)无法使Xi(t)得到更新,则应用Xi′(t)随机更新Xi(t)邻居中比Xi′(t)劣质的某一个个体。 3.5教师的自我提高 Tizhoosh[14]提出了反向学习(opposition based learning,OBL)的概念,并给出了反向学习的算法描述。作者随后的研究报告指出反向解较当前解更为靠近最优解,该几率几乎是50%。现实生活中,教师通常会通过自学习机制,提升自身水平,而在标准TLBO算法中,教师个体则缺少自我学习和提高。考虑到反向学习具有较好的勘探未知解的能力,故令教师个体执行反向学习。 定义3[14]反向解:设在区间[a,b]上存在一个实数x,则x的反向数定义为x′=a+b-x。鉴于此,假设在R域上存在某N维点X=(x1,x2,…,xi,…,xN),并且 xi∈[ai,bi],则定义 X′=(x1′,x2′,…,xi′,…,xN′)为 X的反向点。其中,xi′=k×(ai+bi)-xi,k为[0,1]之间分布均匀的随机数,称作一般化系数。 定义4基于反向解的优化:设待优化问题为minf(x),存在某个可行解 X及其反向解 X′,若f(X′) 算法3 OBL算法 输入:Xi(t),所在区间为[a,b],迭代次数itermax。 输出:Xi(t)。 步骤1迭代次数t=0。 步骤2依据定义1,在迭代次数内经过多次迭代生成反向解种群POP(t)。 步骤3在Xi(t)和POP(t)中选择最优的个体替换Xi(t),输出并结束算法。 按照如下方法使用动态边界。设个体Xij的搜索空间 j维的固定边界为[aj,bj],相应的 j维的动态边界定义为min(aij),max(aij)。在一个N维空间中,Xbest= (x1,x2,…,xi,…,xN),其反向解定义为xi′=k×(ai+bi)-xi,xi∈[min(aij),max(aij)],k∈[0,1],为服从均匀分布的随机数。 3.6算法实现 算法4小世界邻域教与学优化(S-TLBO)算法 输入:种群POP(0),迭代次数n。 输出:最优个体Xbest(t)。 步骤1初始化算法的参数,在解空间内随机产生初始种群POP(0),迭代计数器t=0。 步骤2应用算法2构建小世界网络。 步骤3选择班级种群内的最优个体设为教师Xtea(t)。 步骤4计算班级的平均分Xmean(t),平均适应度f,计算教师对学生个体执行“教”的概率,并依据式(2)对学生执行“教”行为。 步骤5个体Xi(t)依据3.4节执行“学”行为。 步骤6如果教师的状态长时间得不到更新,则教师个体执行OBL算法。 步骤7算法满足结束条件,则输出Xbest(t),结束算法;否则转步骤3。 在S-TLBO算法中,整体种群组成了一个小世界网络,个体之间的“学”行为是向自己的邻居(或邻居的邻居等)进行学习,使这种学习具有了一定的目的性和偏好,加速了算法的收敛,同时也保证了一定程度上的随机性。 4.1非约束函数上的测试 为了验证算法的有效性,将S-TLBO算法应用C语言编码,并在VC6下编译执行,选择AFSA(artificial fish swarm algorithm)[15]、TLBO算法以及两个经典的改进TLBO算法(ITLBO[2]、ETLBO[5])参与对比。AFSA算法的视野范围visual=4,移动步长step= 1.2,拥挤度因子delta=0.3,尝试次数try_number=5。所有算法的种群均设置为30,其他参数参考相关文献进行设置。用于测试的9个Benchmark函数列于表1,包括了多个单峰和多峰函数。实验中将待优化函数设为50维和200维,f1~f6的迭代次数是1 000次,f7~f9的迭代次数为5 000次,分别测试算法在高维和低维度函数上的寻优效果。将5个算法独立运行30次,分别取平均值M,收敛成功的次数N,解方差D,求解结果分别列于表2和表3。 Table 1 Testing functions表1 测试函数列表 首先分析当函数是50维时的表现。f1是一个单峰函数,只有一个全局最优值,比较容易优化。由表2中的数据可以看出,AFSA算法的解精度和解方差均比较差,且收敛成功的次数为0,而本文提出的S-TLBO算法的表现则是5个算法中最优的,其不仅解精度最高,解方差也最小,成功收敛的次数也是最高的。在 f2函数上,S-TLBO算法在解的均值上的表现仍然相对其他参与对比的算法优秀,但是其解方差要低于ETLBO和ITLBO两个算法,优于AFSA算法。在 f3函数上,S-TLBO算法仍然保持了较高的精度和收敛成功率,并且解的方差也要优于其他4个算法。f4函数是一个难以优化的多峰函数,S-TLBO算法的表现较ETLBO稍差,但是仍然要优于AFSA和TLBO两个算法,与ITLBO算法基本相当。在 f5函数的测试上,S-TLBO算法表现出了较高的解精度和解方差。f6仍然是一个多峰函数,主要用于测试算法逃脱局部最优约束的能力,从表中所列数据可以看出,在此函数上,S-TLBO算法表现得较好,是全部5个算法中表现最优的。f7、f8、f9均是多峰函数,3个函数在其解空间内均存在多个局部极值,对算法逃脱局部极值约束的能力要求较高,尤其是 f9函数,在距离最优解3.14距离处存在无穷个局部极值,且强烈震荡。在 f7函数上,所有5个算法的成功率均为0,但是从解精度看,TLBO相关的4个算法的精度还是较AFSA算法高,最好的是ETLBO算法,其次是S-TLBO算法,在解精度的指标上,S-TLBO算法是最好的。在 f8函数上,TLBO及其改进算法表现得几乎是一致的,解精度相当接近,说明TLBO算法本身的求解机制非常适合求解该函数,优化后解的改进效果不明显,S-TLBO算法的表现也一般。在 f9函数上,S-TLBO算法的优越性得以体现,其解精度和解方差明显优于其他4个算法,在迭代次数内已经非常接近最优值,考虑到 f9具有强烈震荡性,说明S-TLBO算法能够非常好地摆脱该函数的局部最优约束和震荡的影响。 其次,分析函数维度增加到200时5个算法的表现。从表3所列数据可以看出,在维度增加到比较高的200时,几乎所有算法的求解能力均有所下降,在f1、f3、f4函数上,S-TLBO算法并没有表现最好,解精度较ITLBO或ETLBO算法略低,基本在一个数量级。在 f2、f5、f6函数上的解精度则是最好的。在f2、f3、f4、f5函数上的方差最好,在 f1函数上的方差劣于ITLBO,在 f6函数上的方差劣于ETLBO。在f7函数上,S-TLBO算法的解精度、解方差均是最优的。因为 f8、f9函数的维度是固定的,测试数据基本没有变化。 分别对比5个算法达到指定收敛精度时的迭代次数和时间。函数为50维时 f1~f6的精度为0.01,f7~f9的精度为10,200维时 f1~f9的精度为0.1,数据列于表4和表5。表中的“—”表示该算法在所设定迭代次数内没有达到指定的收敛精度,D=200时因为AFSA难以在设定迭代次数(10 000)内达到指定要求,所以不再对比AFSA。从表4所列数据可以看出,S-TLBO算法在9个函数上达到设定的精度,所需的迭代次数是最小的,但是时间却不是最小的。这是因为S-TLBO算法中增加了生成复杂网络的操作,同时也调整了教师的教行为,所以较其他相关算法的运行时间多一些。而AFSA、TLBO算法在3个多峰函数上没有收敛到指定的精度。当维度为200时,TLBO算法在 f4、f5、f9函数上没有达到设定精度。其他3个算法的迭代次数与消耗时间均有所增加,但S-TLBO算法所需迭代次数仍然较少,在时间上虽然不是最少,但是与其他两个算法基本相差无几。 Table 2 Comparison of mean,convergence number and variance for unconstrained benchmark functions(Dim=50)表2 在非约束函数上算法的求解均值、成功收敛次数和方差(Dim=50) Table 3 Comparison of mean,convergence number and variance results for unconstrained benchmark functions(Dim=200)表3 在非约束函数上算法的求解均值、成功收敛次数和方差(Dim=200) 为了更为形象地对比算法的收敛性能,绘制了全部参与对比实验的5个算法的收敛曲线图。限于篇幅,仅列出其中的 f1~f6函数图。收敛图使用的数据是取算法30次实验中最好一次和最差一次的平均值,函数维度为50。6个收敛图分别如图1~图6所示。从收敛曲线可以看出,S-TLBO算法的收敛曲线是很平滑的,而且下降速度非常快,在所有的6个函数上明显优于AFSA和标准TLBO算法,对比ETLBO 和ITLBO算法也可以看出S-TLBO算法明显具有一定的优势。 4.2约束函数的测试 为了对比得更加全面,继续选择文献[6]中的5个约束函数进行测试(本文分别对应 f10~f14)。参与测试算法的参数设置与3.1节相同,4个算法各自独立运行30次,取最优值、平均值和解方差进行对比,实验结果列于表6。由表6中所列实验结果可以看出,S-TLBO算法在求解约束函数的实验中表现优秀,f10、f12两个函数找到了最优解,在其他3个函数上找到的最优解、平均值和解方差也均是4个算法中最优的,比标准的TLBO算法有了非常大的提高。 Table 4 Interation number and cost time(Dim=50)表4 算法的平均迭代次数和时间(Dim=50) Table 5 Interation number and cost time(Dim=200)表5 算法的平均迭代次数和时间(Dim=200) Fig.1 Convergence curves of algorithms inf1图1 f1函数上的收敛曲线 Fig.2 Convergence curves of algorithms inf2图2 f2函数上的收敛曲线 Fig.3 Convergence curves of algorithms inf3图3 f3函数上的收敛曲线 Fig.4 Convergence curves of algorithms inf4图4 f4函数上的收敛曲线 Fig.5 Convergence curves of algorithms inf5图5 f5函数上的收敛曲线 Fig.6 Convergence curves of algorithms inf6图6 f6函数上的收敛曲线 Table 6 Results of constrained benchmark functions表6 在约束函数上的测试结果比较 综合以上实验结果与分析可以看到,虽然S-TLBO算法在某些函数上的性能指标不是最佳的,但是无论是对低维函数还是高维函数,S-TLBO算法整体的表现都是非常稳定的,在约束函数的测试中,也明显优于其他算法。 本文提出了一种邻域为小世界网络结构的改进教与学优化算法。基于WS算法将种群进行了小世界网络构建。在教学阶段中,学生基于概率向教师学习,该概率由学生个体的适应度和教师适应度计算而得,学习后应用临时状态直接更新原状态。在互相学习过程中,学生在自己的直接邻居节点或间接邻居节点中随机选择个体进行学习。为了提高最佳个体的勘探新解和开采能力,引入了教师个体的反向学习。在多个约束函数和非约束函数上的实验表明,本文算法的求解能力较标准TLBO算法有了较大幅度的提高,适合求解较高维度连续函数的优化问题。邻域结构是影响群体智能算法效率的重要因素之一,将进一步深入研究不同邻域结构下TLBO的求解能力。同时,研究其与经典演化算法的相互结合模式,拓展其应用领域,亦是重要的研究方向。 References: [1]Chen Debao,Zou Feng,Li Zheng.An improved teachinglearning-based optimization algorithm for solving global optimization problem[J].Information Sciences,2015,297: 171-190. [2]Kundu S,Biswas S,Das S,et al.A selective teaching-learning based niching technique with local diversification strategy [C]//LNCS 7677:Proceedings of the 3rd International Conference on Swarm,Evolutionary,and Memetic Computing, Bhubaneswar,India,Dec 20-22,2012.Berlin,Heidelberg: Springer,2012:160-168. [3]Rao R V,Patel V.An improved teaching learning based optimization algorithm for solving unconstrained optimization problems[J].Scientia Iranica,2013,20(3):710-720. [4]Li Junqing,Pan Quanke,Mao Kun.A discrete teachinglearning-based optimisation algorithm for realistic flowshop rescheduling problems[J].Engineering Applications ofArtificial Intelligence,2015,37:279-292. [5]Rao R V,Patel V.An elitist teaching learning based optimization algorithm for solving complex constrained optimization problems[J].International Journal of Industrial Engineering Computations,2012,3(4):535-560. [6]Yu Kunjie,Wang Xin,Wang Zhenlei.Elitist teaching-learningbased optimization algorithm based on feedback[J].Acta Automatica Sinica,2014,40(9):1976-1983. [7]Rajasekhar A,Rani R,Ramya K,et al.Elitist teachinglearning opposition based algorithm for global optimization [C]//Proceedings of the 2012 IEEE International Conference on Systems,Man,and Cybernetics,Seoul,Oct 14-17, 2012.Piscataway,USA:IEEE,2012:1124-1129. [8]Rao R V,Patel V.Multi objective optimization of two stage thermoelectric coolers using a modified teaching-learningbased optimization algorithm[J].Engineering Applications ofArtificial Intelligence,2013,26(1):430-445. [9]Nayak J,Naik B,Kanungo D P,et al.A hybrid elicit teaching learning based optimization with fuzzy C-means algorithm for data clustering[J].Ain Shams Engineering Journal,2016 (5):148-156. [10]Durai S,Subramanian S,Ganesan S.Improved parameters for economic dispatch problems by teaching learning optimization[J].Electrical Power and Energy Systems,2015, 67:11-24. [11]Sahu B K,Pati T K,Nayak J R,et al.A novel hybrid LUSTLBO optimized fuzzy-PID controller for load frequency control of multi-source power system[J].Electrical Power and Energy Systems,2016,74:58-69. [12]Dokeroglu T.Hybrid teaching-learning-based optimization algorithms for the quadratic assignment problem[J].Computers&Industrial Engineering,2015,85:86-101. [13]Li Wenbin,Chen Yiying,He Yichao,et al.New different evolution with neighborhood structure based on complex network[J],Application Research of Computers,2016,32 (2):370-374. [14]Tizhoosh H R.Opposition-based learning:a new scheme for machine intelligence[C]//Proceedings of the 2005 IEEE International Conference on Computational Intelligence for Modelling,Control and Automation,Vienna,Nov 28-30, 2005.Piscataway,USA:IEEE,2005:695-701. [15]Wang Peichong.Swarm intelligence algorithms and their applications[M].Beijing:Publishing House of Electronics Industry,2015. 附中文参考文献: [6]于坤杰,王昕,王振雷.基于反馈的精英教学优化算法[J].自动化学报,2014,40(9):1976-1983. [13]李文斌,陈嶷瑛,贺毅朝,等.邻域结构为复杂网络的差分演化算法[J].计算机应用研究,2016,32(2):370-374. [15]王培崇.群体智能算法及其应用[M].北京:电子工业出版社,2015. WANG Peichong was born in 1972.He received the Ph.D.degree from China University of Mining and Technology (Beijing)in 2010.Now he is an associate professor at College of Information Engineering,Hebei GEO University, and the member of CCF.His research interests include evolutionary computation,machine learning and pattern recognization,etc.He has published more than 30 papers in domestic and international journals and conferences. 王培崇(1972—),男,河北辛集人,2010年于中国矿业大学(北京)计算机应用技术专业获得博士学位,现为河北地质大学信息工程学院副教授,CCF会员,主要研究领域为进化计算,机器学习,模式识别等。发表学术论文30余篇。 MAYue was born in 1993.She is an M.S.candidate at Hebei GEO University.Her research interests include artificial intelligence and machine learning,etc. 马玥(1993—),女,山东潍坊人,河北地质大学硕士研究生,主要研究领域为人工智能,机器学习等。 GENG Mingyue was born in 1994.She is an M.S.candidate at Chongqing University of Posts and Telecommunications,and the student member of CCF.Her research interest is digital image processing. WANG Shenwen was born in 1979.He received the Ph.D.degree from Wuhan University in 2014.Now he is an associate professor at College of Information Engineering,Hebei GEO University.His research interests include evolutionary computation and machine learning,etc. 汪慎文(1979—),男,湖北红安人,2014年于武汉大学计算机学院获得博士学位,现为河北地质大学信息工程学院副教授,主要研究领域为演化计算,机器学习等。 New Teaching-Learning-Based Optimization with Neighborhood Structure Based on Small Worldƽ WANG Peichong1,2+,MAYue1,GENG Mingyue3,WANG Shenwen1 WANG Peichong,MA Yue,GENG Mingyue,et al.New teaching-learning-based optimization with neighborhood structure based on small world.Journal of Frontiers of Computer Science and Technology,2016,10(9):1341-1350. Teaching-learning-based optimization(TLBO)is a recently proposed swarm intelligent algorithm that simulates the process of teaching and learning.Concerning the problems that TLBO is easy to premature,low solution precision,slow convergence speed of weakness,this paper proposes an improved TLBO named S-TLBO(small world neighborhood TLBO).S-TLBO adopts small world network as its spatial structure,and individuals of S-TLBO is looked as the nodes of network.In teaching phase,student individuals learn from teacher individual based on probability,and they learn from their neighbor nodes which are better in learning phase.The best in dividual exe-cutes opposition based learning(OBL)algorithm to exploiting and exploring.Some experiments are conducted on many classical testing functions,the results show that the improved algorithm has superior global convergence and higher precision,especially fits for solving multimode and high dimension function optimization problems. 2016-04,Accepted 2016-06. teaching-learning-based optimization(TLBO);small world network;neighborhood structure;opposition based learning(OBL) *The National Natural Science Foundation of China under Grant No.61402481(国家自然科学基金);the Natural Science Foundation of Hebei Province under Grant No.F2015403046(河北省自然科学基金);the Key Research Plan of Hebei Province under Grant No. 15210710(河北省重点研发计划). CNKI网络优先出版:2016-06-02,http://www.cnki.net/kcms/detail/11.5602.TP.20160602.1144.010.html A TP301.6

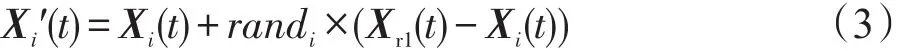
4 仿真实验与分析







5 结束语




1.College of Information Engineering,Hebei GEO University,Shijiazhuang 050031,China
2.College of Mechanical Electronic and Information Engineering,China University of Mining and Technology,Beijing 100083,China
3.College of Computer,Chongqing University of Posts and Telecommunications,Chongqing 400065,China
+Corresponding author:E-mail:wpeichong@126.com

