高效可证明安全的无证书代理签名方案*

汤永利，王菲菲，叶　青，闫玺玺

河南理工大学 计算机科学与技术学院，河南 焦作 454000

高效可证明安全的无证书代理签名方案*

汤永利+，王菲菲，叶青，闫玺玺

河南理工大学 计算机科学与技术学院，河南 焦作 454000

无证书密码体制；代理签名；椭圆曲线离散对数难题；随机预言机模型

1　引言

Al-Riyami和Paterson[1]于2003年提出了无证书公钥密码体制，继承了基于身份密码体制无需公钥证书的优点，同时解决了基于身份密码体制的密钥托管问题。

Mambo等人[2-3]于1996年提出代理签名，签名人在无法行使签名权时，将签名权力委托给信任的代理人，由代理人代表原始签名人行使签名权。

无证书代理签名结合了无证书密码体制与代理签名的优点，既不需要证书来认证用户公钥的真实性，节约了管理证书所需的各种资源，又可使签名人在不方便行使签名权力时，将签名权转交给信任的代理人。无证书代理签名的种种优点，使它广泛应用于电子商务、分布式共享系统、网格计算、移动代理系统、全球分布网络等场合[4]。

2005年，Li等人[5]提出了首个基于双线性对的无证书代理签名方案。2007年，Lu等人[6]指出Li[5]的方案不安全，并提出了改进方案。文献[5]与文献[6]均没有给出方案的形式化安全性证明。2009年，陈虎等人[7]提出了无证书代理签名方案的安全模型，并基于计算Diffie-Hellman问题提出了一个无证书代理签名方案，给出了针对超级攻击者的安全性证明。之后，为提高方案的计算效率与安全性，文献[8]、文献[9]、文献[10]相继提出了基于双线性对的无证书代理签名方案，给出了形式化安全性证明。其中，文献[10]方案计算效率最优。

由于双线性对运算比较耗时，提出了不依赖双线性对的无证书代理签名方案。2010年，许春根等人[11]提出了一个不使用双线性对的无证书代理签名方案，其安全性基于离散对数困难问题，计算效率较高。最近，Deng等人[12]基于RSA提出了一个无证书代理签名方案，给出了针对超级攻击者的安全性证明，方案的计算效率主要依赖于模幂运算。

为了提高无证书代理签名方案的计算效率，在王亚飞等人[13]的无证书签名方案的基础上，本文提出一个高效的无证书代理签名方案，方案的安全性基于椭圆曲线离散对数问题（elliptic curve discrete logarithm problem，ECDLP）。在陈虎等人[7]提出的安全模型下给出了针对超级攻击者的安全性证明，方案的安全性是抗存在性伪造的。本文方案在计算效率上有很大提高。

2　预备知识

2.1数学困难问题

椭圆曲线离散对数问题：给定椭圆曲线E(Fq)，G 为E(Fq)的一个循环子群，P为G的一个生成元，P的阶为n，给定Q∈G，求满足Q=[x]P的唯一整数x。

2.2无证书代理签名及安全模型

无证书代理签名方案中，设原始签名人的身份标识为A，公钥为PKA。代理签名人的身份标识为B，公钥为PKB。A将授权许可信息mw和部分代理钥θ发送给B，B生成消息m的代理签名σ。

无证书代理签名方案包括系统参数生成、部分私钥生成、秘密值生成、用户私钥生成、用户公钥生成、部分代理钥生成、部分代理钥验证、代理钥生成、代理签名及验证10个算法。

陈虎等人[7]提出的无证书代理签名安全模型中，第一类攻击者α1具备的能力是：不知道系统主密钥，能够对用户公钥进行替换；第二类攻击者α2具备的能力是：知道系统主密钥，无法对用户公钥进行替换。

挑战者D和攻击者α1、攻击者α2进行如下游戏。

初始化：运行系统参数生成算法，输入安全参数，输出系统参数和系统主密钥。将系统参数发送给α1，系统主密钥对α1严格保密；将系统参数和系统主密钥发送给α2。

α1或α2可以适应性地进行多项式次数的用户生成询问、部分私钥询问、公钥替换询问、秘密值询问、部分代理钥询问、代理钥询问、代理签名询问。

伪造：最后攻击者输出元组(mw,A,PKA,θ)或(m,mw,A,PKA,B,PKB,σ)作为它的伪造。若能满足下列情况之一，说攻击者赢得了这个游戏。

情况1元组(mw,A,PKA,θ)满足：

（1）(params,mw,A,PKA,θ)是有效的部分代理钥；

（2）若攻击者为α1，不曾询问原始签名人A的部分私钥，若攻击者为α2，不曾询问A的秘密值；

（3）(mw,A,PKA)没有进行过部分代理钥询问。

情况2元组(m,mw,A,PKA,B,PKB,σ)满足：

（1）(params,m,mw,A,PKA,B,PKB,σ)是有效的代理签名；

（2）若攻击者为α1，不曾询问原始签名人A的部分私钥；若攻击者为α2，不曾询问A的秘密值；

（3）(mw,A,PKA)没有进行过部分代理钥询问；

（4）(m,mw,A,PKA,B,PKB,σ)没有进行过代理钥询问；

（5）(m,mw,A,PKA,B,PKB,σ)没有进行过签名询问。

情况3元组(m,mw,A,PKA,B,PKB,σ)满足：

（1）(params,m,mw,A,PKA,B,PKB,σ)是有效的代理签名；

（2）若攻击者为α1，不曾询问代理签名人B的部分私钥；若攻击者为α2，不曾询问B的秘密值；

（3）(m,mw,A,PKA,B,PKB,σ)没有进行过代理钥询问；

（4）(m,mw,A,PKA,B,PKB,σ)没有进行过签名询问。

定义1一个无证书代理签名方案在适应性选择身份和消息攻击下是存在性不可伪造的，当且仅当在多项式时间内，任何攻击者均不能以不可忽略的概率赢得以上游戏。

3　无证书代理签名方案

本文提出一种新的无证书代理签名方案，由系统参数生成、用户密钥生成、代理密钥生成、代理签名和验证几个算法构成。

（1）系统参数生成

输入安全参数k，选择两个大素数p、q，满足q|p-1。P为循环群G中一个阶为q的生成元，选择安全的Hash函数：。KGC选择系统主密钥s，计算系统公钥PPUB=sP公开系统参数params={p,q,G,P,PPUB, H1,H2,H3,H4}，秘密保存系统主密钥s。

（2）用户密钥生成

②KGC把部分私钥DID和部分公钥RID安全地传送给用户，用户收到后，验证DIDP=RID+PPUBH1(ID,RID)是否成立，若成立，则DID是有效的用户部分私钥，否则，判定DID无效。

（3）代理密钥生成

假定原始签名人的身份标识为A，代理签名人的身份标识为B，A委托B进行代理签名，A产生授权许可信息mw，此授权信息包含A的身份信息以及A和B的授权关系，也包含该代理签名的使用限制等内容。

②部分代理钥验证：B收到θ后，计算 h1=，验证SPP=RA+PPUBh1+ XAh2+I是否成立，若成立，则θ是有效的部分代理钥，否则，判定θ无效。③代理钥SW=(SP,I,SKB)。

（4）代理签名

①B选取随机数z∈Zq*，计算Z=zP。

②计算h3=H3(B,RB,XB)。

③计算h4=H4(m,mw,Z,I,A,B,RA,XA,RB,XB)。

④计算u=z+SP+DBh3+xBh4。

⑤对消息m的签名为σ=(I,Z,u)。

（5）验证

假定R为消息的接受者，R收到消息m和m的签名σ以后：

①计算h0=H1(B,RB)。

②计算h1=H1(A,RA)。

③计算h2=H2(I,mw,A,RA,XA)。

④计算h3=H3(B,RB,XB)。

⑤计算h4=H4(m,mw,Z,I,A,B,RA,XA,RB,XB)。

⑥计算Z′=uP-(RA+PPUBh1+XAh2+I+RBh3+PPUBh0h3+XBh4)。

⑦验证Z=Z′是否成立。若成立，则签名σ为有效的；否则，签名无效。

4　安全性证明

定理1在随机预言模型下，若第一类超级攻击者α1能够在多项式时间内以不可忽略的概率成功攻破本文方案，那么存在一个算法C在多项式时间内能够以的概率解决ECDLP的一个实例。

证明 假设C是解决ECDLP问题的一个有效算法，其输入为（P,aP），目标是求取a的值。C利用α1（α1为第一类超级攻击者）作为子程序试图解决ECDLP问题。假设α1最多能做qC次用户生成询问，C随机选择

α1适应性地进行多项式次数的以下询问。

用户生成询问：C创建列表LC，列表元组定义为(ID,RID,DID,xID,XID)。对某一ID进行用户生成询问，若LC中已存在对应元组(ID,RID,DID,xID,XID)，则返回PKID给α1。否则，按以下步骤生成用户：

H1询问：C维护列表LH1，当C收到α1对H1(ID,RID)的查询时查看列表LH1中是否存在对应元组(ID,RID, h1)，若存在，返回h1给α1；若不存在，C选取随机数，返回h1给α1，并在LH1中添加元组(ID,RID,h1)。

H2询问：C模拟H2随机预言机，创建列表LH2，初始化为空，列表元组定义为(I,mw,ID,RID,XID,h2)。C收到α1对H2(I,mw,ID,RID,XID)的查询时，查看列表LH2中是否存在对应元组(I,mw,ID,RID,XID,h2)，若存在，返回h2给α1；若不存在，C选取随机数h2∈，返回h2给α1，并在LH2中添加元组(I,mw,ID,RID,XID,h2)。

H3询问：C模拟H3随机预言机，创建列表LH3，初始化为空，列表元组定义为(ID,RID,XID,h3)。当C收到α1对H3(ID,RID,XID)的查询时查看LH3中是否存在对应元组(ID,RID,XID,h3)，若存在，返回h3给α1；若不存在，C选取随机数h3∈，返回h3给α1，并在LH3中添加元组(ID,RID,XID,h3)。

H4：C模拟H4随机预言机，创建列表LH4，初始化为空，列表元组定义为(m,mw,Z,I,A,B,RA,XA, RB,XB,h4)。当C收到α1的H4询问时，查看在LH4中是否存在对应元组(m,mw,Z,I,A,B,RA,XA,RB,XB,h4)，若存在，返回h4给α1；若不存在，C选取随机数h4∈，返回h4给α1，并在LH4中添加元组(m,mw,Z,I,A, B,RA,XA,RB,XB,h4)。

部分私钥询问：C收到α1对某一ID的部分私钥询问，若ID=J，则C终止，否则，查看在列表LC中是否存在对应的元组(ID,RID,DID,xID,XID)，若存在，返回DID给α1；若不存在，则先进行用户生成询问，再返回DID给α1。

公钥替换询问：C收到α1对某一ID的公钥替换询问(ID,XID')，检索列表LC找到对应元组(ID,RID, DID,xID,XID)，将XID替换为XID'，令xID=⊥。

秘密值询问：C收到α1对某一ID的秘密值询问，检索列表 LC找到对应元组(ID,RID,DID,xID,XID)，若xID=⊥，表明此ID的公钥已被替换，因此C无法回答α1的秘密值询问，C返回⊥；否则，C返回xID。

部分代理钥询问：C收到α1的某一部分代理钥询问(mw,A)，随机选择SP,h2∈，计算h1=H1(A,RA)，I=SPP-(RA+PPUBh1+XAh2)。将部分代理钥θ=(I,SP)返回给α1，并在列表LH2中添加元组(I,mw,ID,RID,XID,h2)。代理钥询问：C收到α1的某一代理钥询问(mw,A,B)，先对(mw,A)进行部分代理钥询问，得到θ=(I,SP)。若B=J，则C终止，否则，查询列表LC找到B的对应元组返回代理钥 SW= (SP,I,SKB)给代理签名询问：C收到α1的某一代理签名询问(m,mw,A,B)，查询列表 LC找到A、B的对应元组(A,RA,DA,xA,XA)和(B,RB,DB,xB,XB)。随机选择，计算I=SPP-(RA+PPUBh1+XA，返回签名最后，α1输出元组(mw,A,PKA,θ)或(m,mw,A,PKA, B,PKB,σ)作为它的伪造。

（1）伪造的有效元组(mw,A,PKA,θ=(I,SP))满足2.2节定义的情况1。若A≠J，则C终止；否则，根据分叉引理[14]，在选择相同的随机数的情况下，选择不同的Hash函数H1，可以得到另外一个有效的伪造(mw,A,PKA,θ′=(I,SP'))，则有以下等式成立：联立上面两个式子求得（2）伪造的有效元组Z,u))满足2.2节定义的情况2。若A≠J，则C终止；否则，根据分叉引理，在选择相同的随机数的情况选择不同的Hash函数H1，可以得到另外一个有效的伪造，则有以下等式成立：联立上面两个式子求得（3）伪造的有效元组Z,u))满足2.2节定义的情况3。若B≠J，则C终止；否则，根据分叉引理，在选择相同的随机数的情况下，选择不同的Hash函数H3，可以得到另外一个有效的伪造，则有以下等式成立：联立上面两个式子求得。C利用α1作为子程序成功地解决了ECDLP问题。概率分析：分析能导致C成功的3个事件。

E1：C没有在进行部分私钥询问或代理钥询问时终止。

E2：α1能够伪造一个有效的部分代理钥或代理签名。

E3：E2发生，并满足以下条件中的一个：

（1）输出的有效元组(mw,A,PKA,θ)满足A=J；（2）输出的有效元组满足A=J；

（3）输出的有效元组(m,mw,A,PKA,B,PKB,σ)满足B=J。

假设α1在多项式时间内至多可进行qC次用户生成询问，qppk次部分私钥询问，qprok次代理钥询问，则有：那么C解决ECDLP的概率为：

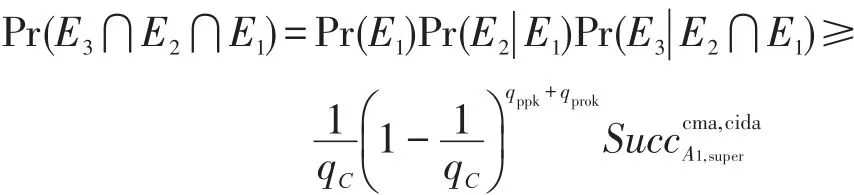
定理2在随机预言模型下，若第二类超级攻击者α2能够在多项式时间内以不可忽略的概率成功攻破本文方案，那么存在一个算法C在多项式时间内能够以

证明 假设C是解决ECDLP问题的一个有效算法，其输入为(P,aP)，目标是求取a的值。C利用α2（α2为第二类超级攻击者）作为子程序试图解决ECDLP问题。假设α2最多能做qC次用户生成询问，C随机选择J∈[1,qC]作为这次游戏的挑战身份。

α2适应性地进行多项式数次数的以下询问。

用户生成询问：C创建列表LC，列表的元组定义为(ID,RID,DID,xID,XID)，对某一若列表LC中存在对应元组(ID,RID,DID,xID,XID)，则返给α2，否则，按以下步骤生成用户：

H1询问、H2询问、H3询问、H4询问、公钥替换询问、部分代理钥询问、代理钥询问、代理签名询问同定理1。

部分私钥询问：C收到α2对某一ID的部分私钥询问，查看列表 LC中是否存在对应元组(ID,RID, DID,xID,XID)，若存在，返回DID给α2；若不存在，则先进行用户生成询问，再返回DID给α2。

秘密值询问：C收到α2对某一ID的秘密值询问，若ID=J，则C终止；否则，查看列表LC中是否存在对应元组(ID,RID,DID,xID,XID)，若存在，返回xID给α2；若不存在，则先进行用户生成询问，再返回xID给α2。

最后，α2输出元组(mw,A,PKA,θ)或(m,mw,A,PKA, B,PKB,σ)作为它的伪造。

（1）伪造的有效元组(mw,A,PKA,θ=(I,SP))满足2.2节定义的情况1。若A≠J，C终止；否则，根据分叉引理，在选择相同的随机数的情况下，选择不同的Hash函数H2，可以得到另外一个有效的伪造(mw,A, PKA,θ′=(I,SP'))，则有以下等式成立：

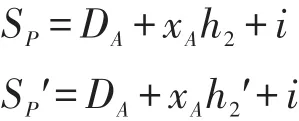
（2）伪造的有效元组(m,mw,A,PKA,B,PKB,σ=(I, Z,u))满足2.22。若A≠J，C终止；否则，根据分叉引理，在选择相同的随机数的情况下，选择不同的Hash函数H2，可以得到另外一个有效的伪造，则有以下等式成立：

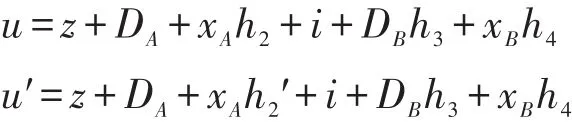
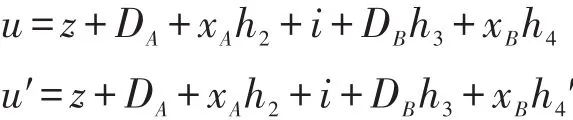
概率分析：分析能导致C成功的3个事件。

E1：C没有在进行秘密值询问或代理钥询问时终止。

E2：α2能够伪造一个有效的部分代理钥或代理签名。

E3：E2发生，并满足以下条件中的一个：

（1）输出的有效元组(mw,A,PKA,θ)满足A=J；

（2）输出的有效元组(m,mw,A,PKA,B,PKB,σ)满足A=J；

（3）输出的有效元组(m,mw,A,PKA,B,PKB,σ)满足B=J。

假设α2在多项式时间内至多可进行qC次用户生成询问，qsv次秘密值询问，则有

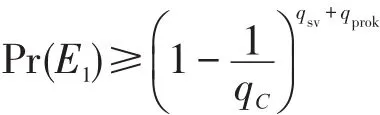
Table 1　Efficiency comparison of this paper scheme with other schemes表1　本文签名方案与已有签名方案的比较

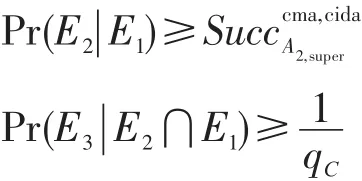
那么C解决ECDLP的概率为：

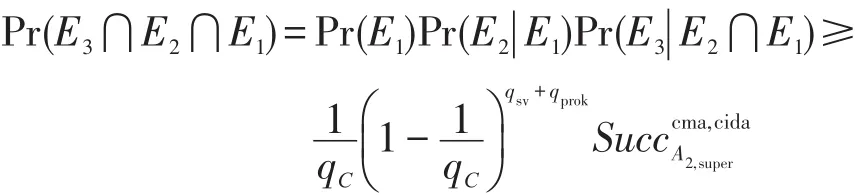
5　效率对比分析

把本文方案与目前效率最高的无证书代理签名方案进行效率对比，结果如表1所示。

用P表示一个双线性对运算，G表示一个基于双线性对的点乘运算，E表示一个模幂运算，S表示一个标量乘运算。参考文献[12]的实验数据，计算一个双线性对运算所消耗的时间为20.01 ms，计算一个基于双线性对的点乘运算所消耗的时间为6.38 ms，计算一个模幂运算所消耗的时间为11.20 ms，计算椭圆曲线上一个标量乘运算所消耗的时间为0.83 ms。根据文献[12]的方法估算各个方案的计算效率[12]在代理签名阶段需要一个标量乘运算和两个模幂运算，计算所需时间为0.83+2×11.20=23.23ms。

在代理签名阶段，本文方案的计算量是文献[10]方案的13.0%，文献[11]方案的7.4%，文献[12]方案的3.6%。本文方案的计算量是文献[10]方案的5.3%，文献[11]方案的8.8%，文献[12]方案的20.7%。本文方案在计算效率上有很大的提高。

6　结束语

本文提出了一种新的无证书代理签名方案，方案的安全性基于椭圆曲线离散对数困难问题，计算效率明显优于现有的无证书代理签名方案，且签名长度较短。本文方案能够抵抗第一类超级攻击者、第二类超级攻击者的适应性选择消息攻击，具有很强的安全性。

本文方案拥有很高的计算效率，需要很少的存储空间，适用于对计算和存储等资源有严格限制的场合。例如，在移动代理系统中，经常使用代理签名，但由于终端的存储能力和计算能力有限，证书的存储要占用存储资源，证书的验证也要花费通信代价，这些对能力有限的系统终端都是很大的负担。使用无证书代理签名，无需证书的存储与验证，能很好地满足他们的需求。

References:

[1]Al-Riyami S S,Paterson K G.Certificateless public key cryptography[C]//LNCS 2894:Proceedings of the 9th International Conference on the Theory andApplication of Cryptology and Information Security,Taipei,China,Nov 30-Dec 4,2003.Berlin,Heidelberg:Springer,2003:452-473.

[2]Mambo M,Usuda K,Okamoto E.Proxy signatures for delegating signing operation[C]//Proceedings of the 1996 ACM Conference on Computer and Communications Security, New Delhi,India,Mar 1996.New York:ACM,1996:48-57.

[3]Mambo M,Usuda K,Okamoto E.Proxy signatures:delegation of the power to sign messages[J].IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences,1996,E79-A(9):1338-1354.

[4]Shi Wenbo,He Debiao,Gong Peng.On the security of a certificateless proxy signature scheme with message recovery[J].Mathematical Problems in Engineering,2013,57(9/10): 2510-2518.

[5]Li X,Chen K,Sun L.Certificateless signature and proxy signature schemes from bilinear pairings[J].Lithuanian Mathematical Journal,2005,45(1):76-83.

[6]Lu Rongbo,He Dake,Wang Changji.Cryptanalysis and improvement of a certificateless proxy signature scheme from bilinear pairings[C]//Proceedings of the 8th ACIS International Conference on Software Engineering,Artificial Intelligence,Networking,and Parallel/Distributed Computing, Qingdao,China,Jul 30-Aug 1,2007.Washington:IEEE Computer Society,2007:285-290.

[7]Chen Hu,Zhang Futai,Song Rushun.Certificateless proxy signature scheme with provable security[J].Journal of Software,2009,20(3):692−701.

[8]Xiong Hu,Li Fagen,Qin Zhiguang.A provably secure proxy signature scheme in certificateless cryptography[J].Informatica,2010,21(2):277-294.

[9]Zhang Lei,Zhang Futai,Wu Qianhong.Delegation of signing rights using certificateless proxy signatures[J].Information Sciences,2012,184(1):298-309.

[10]Seo S H,Choi K Y,Hwang J Y,et al.Efficient certificateless proxy signature scheme with provable security[J].Information Sciences,2012,188:322-337.

[11]Xu Chungen,Zhang Aohong,Han Mu,et al.Certificateless proxy signature scheme based on discrete logarithm problem[J].Journal of Nanjing University of Science and Technology:Natural Science,2010,34(6):733-737.

[12]Deng Lunzhi,Zeng Jiwen,Qu Yunyun.Certificateless proxy signature from RSA[J].Mathematical Problems in Engineering,2014(9).doi:10.1155/2014/373690.

[13]Wang Yafei,Zhang Ruizhe.Strongly secure certificateless signature scheme without pairings[J].Journal on Communications,2013,34(2):94-100.

[14]Pointcheval D,Stern J.Security arguments for digital signatures and blind signatures[J].Journal of Cryptology,2000, 13(3):361-396.

附中文参考文献：

[11]许春根,张傲红,韩牟,等.一种基于离散对数问题的无证书代理签名方案[J].南京理工大学学报:自然科学版, 2010,34(6):733-737.

[13]王亚飞,张睿哲.强安全无对的无证书签名方案[J].通信学报,2013,34(2):94-100.

TANG Yongli was born in 1972.He received the Ph.D.degree in cryptology from Beijing University of Posts and Telecommunications in 2008.Now he is an associate professor at Henan Polytechnic University.His research interests include information security and cryptology,etc.

汤永利（1972—），男，河南孟州人，2008年于北京邮电大学获得博士学位，现为河南理工大学副教授，主要研究领域为信息安全，密码学等。

WANG Feifei was born in 1991.She is an M.S.candidate at Henan Polytechnic University.Her research interest is cryptology.

王菲菲（1991—），女，河南滑县人，河南理工大学硕士研究生，主要研究领域为密码学。

YE Qing was born in 1981.She received the Ph.D.degree in cryptology from Beijing University of Posts and Telecommunications in 2014.Now she is a lecturer at Henan Polytechnic University.Her research interest is cryptology.

叶青（1981—），女，辽宁营口人，2014年于北京邮电大学获得博士学位，现为河南理工大学讲师，主要研究领域为密码学。

YAN Xixi was born in 1985.She received the Ph.D.degree in cryptology from Beijing University of Posts and Telecommunications in 2012.Now she is a lecturer at Henan Polytechnic University.Her research interest is cryptology.

闫玺玺（1985—），女，河南灵宝人，2012年于北京邮电大学获得博士学位，现为河南理工大学讲师，主要研究领域为密码学。

Provably Secure Efficient Certificateless Proxy Signature Schemeƽ

TANG Yongli+,WANG Feifei,YE Qing,YAN Xixi
College of Computer Science and Technology,Henan Polytechnic University,Jiaozuo,Henan 454000,China
+Corresponding author:E-mail:yltang@hpu.edu.cn

TANG Yongli,WANG Feifei,YE Qing,et al.Provably secure efficient certificateless proxy signature scheme. Journal of Frontiers of Computer Science and Technology,2016,10(9):1282-1289.

To improve the computational efficiency,this paper proposes an efficient provably secure certificateless proxy signature scheme based on elliptic curve discrete logarithm problem,avoiding bilinear pairing.The proposed scheme is more computationally efficient than the existing schemes.Its generate-partial-proxy-key algorithm needs one scalar multiplication,its validate-partial-proxy-key algorithm needs two scalar multiplications,and its signing algorithm only needs one scalar multiplication,its validation algorithm only needs six scalar multiplications.Furthermore, its signature length is shorter.The proposed scheme is existentially unforgeable in adaptive chosen message and identity for super adversary,and is particularly suitable for practical applications with limited bandwidth and powerconstrained devices.

certificateless public key cryptography;proxy signature;elliptic curve discrete logarithm problem;random oracle model

为提高无证书代理签名方案的计算效率，提出了一个高效的无证书代理签名方案。该方案的安全性基于椭圆曲线离散对数难题，不使用双线性对，其效率比现有的无证书代理签名方案有很大提高。在部分代理钥生成阶段只需1个标量乘，在部分代理钥验证阶段只需2个标量乘，在代理签名阶段只需1个标量乘，在代理签名验证阶段只需6个标量乘，且签名长度较短。所提方案对于超级攻击者在适应性选择消息与身份下是存在性不可伪造的，适用于对计算和存储等资源有严格限制的实际应用场合。

2016-04,Accepted 2016-06.

*The National Natural Science Foundation of China under Grant No.61300216(国家自然科学基金);the International Science and Technology Cooperation Program of Science and Technology Office of Henan Province under Grant No.152102410048(河南省科技厅国际科技合作计划);the Research of Basic and Advanced Technology of Henan Province under Grant No.142300410147(河南省基础与前沿技术研究);the Natural Science Research Project of Education Department of Henan Province under Grant Nos.12A520021, 16A520013(河南省教育厅自然科学研究项目).

CNKI网络优先出版:2016-06-23,http://www.cnki.net/kcms/detail/11.5602.TP.20160623.1401.022.html

A

TP309