局部信息熵的快速混合测地区域活动轮廓模型*

林喜兰，陈秀宏，肖林云

江南大学 数字媒体学院，江苏 无锡 214122

局部信息熵的快速混合测地区域活动轮廓模型*

林喜兰+，陈秀宏，肖林云

江南大学 数字媒体学院，江苏 无锡 214122

针对变分水平集算法在图像分割过程中计算量较大且收敛速度慢的现象，在前人研究的基础上提出了一种新的局部信息熵的混合测地区域活动轮廓模型。该模型构造一个新的能量泛函，在泛函中引入柔化核函数作为窗口核函数，构造一个新的符号压力函数来代替测地线边缘检测函数，并以局部信息熵作为图像拟合能量项的权重，通过非凸正则化项来约束水平集函数。由此得到的算法不仅能加快轮廓曲线的收敛速度，而且可以处理那些由于光照或其他外界因素的变化产生的灰度不均匀或者模糊的图像，提高分割的精确性。将算法在合成图像和真实图像上做仿真实验，实验结果表明，该算法具有较快的收敛速度，分割也较准确，同时对轮廓曲线的初始位置不敏感，具有很好的鲁棒性。

混合测地区域活动轮廓模型；柔化核函数；符号压力函数；局部信息熵；非凸正则化项

1　引言

图像分割是图像处理和计算机视觉领域的一个基础问题。许多学者已经对此进行了广泛的研究，并提出了多种图像分割算法，其中基于变分偏微分方程[1]的活动轮廓模型是最成功的算法之一。活动轮廓模型算法的基本思想是在一些约束条件下演化轮廓曲线来提取理想的目标。性质，现有的活动轮廓模型图像分割算法分为基于两类。

测地线活动轮廓模型[3]是其中最经典的一种基于边缘的图像分割模型，它使用图像的梯度信息构造一个边缘检测函数来控制轮廓曲线的演化，使其在目标边缘停止演化，从而得到目标的边界。此后，其他一些相关算法通过引入一个气球力项来控制轮廓曲线的收缩和扩张，然而气球力的设计比较困难。由于基于边缘的模型容易得到局部极小值，故当初始轮廓曲线距离目标边界较远时不能够检测到区域的内部和外部边界。

1989年Mumford和Shah[6]提出了基于区域的模型（简称MS模型），但由于计算太复杂而很难应用于实践。后来Chan和Vese[7]对MS模型进行了简化，提出具有里程碑意义的经典Chan-Vese模型（简称CV模型）。后来出现了许多基于此模型的改进模型，其中影响较为广泛的是李纯明教授提出的一系列方法。Li等人在文献[8]中提出了一种能避免水平集函数演化过程中重新初始化的新算法，在文献[4]和[9]中提出了比较经典的RSF（region-scalable fitting）活动轮廓模型和基于距离正则化的活动轮廓模型，并对演化过程中的水平集函数做正则化约束。针对CV模型因光照不均匀与成像设备不完善而导致灰度不均匀图像的分割效果不尽如人意问题，Li等人[13]推导出了一个考虑图像局部灰度聚类性质的一种新的基于区域的方法，它用区域偏移场来修正区域平均灰度。此外，Lankton等人[14]提出的基于区域的混合测地线水平集演化图像分割方法也为变分水平集活动轮廓的图像分割提供了新的思路。后来的研究者也提出了类似的一些改进算法[16]，取得了不错的效果。

与基于边缘的模型相比，基于区域的模型具有许多优势。首先，基于区域的模型使用轮廓区域内部和外部的统计信息来控制曲线演化，对噪声敏感度较低，并且对具有弱边界和没有边界的图像分割效果较好。其次，对初始化轮廓区域位置敏感度相对较低，能有效地分割出目标区域。

针对变分水平集算法在图像分割过程中计算量较大且收敛速度慢的现象，本文在前人研究的基础上[3-4,6-9]，基于区域混合测地线的思路提出了一种新的基于区域的变分水平集图像分割模型——引入局部信息熵的混合测地区域活动轮廓模型（hybrid geodesic region active contour model of local entropy，HGRACM-LE）。该模型首先构造一个新的关于水平集函数的能量泛函，它用一个新的符号压力函数（signed pressure force function，SPF）来代替测地线边缘检测函数，引入柔化核函数作为窗口核函数对图像能量拟合项进行平滑，同时增加了关于水平集函数的非凸正则化项对其进行约束，以便保证水平集函数在演化过程中保持理想的形状。然后，通过求解关于轮廓曲线水平集解能量泛函的欧拉方程得到曲线演化的梯度下降流。最后，使用经典的有限差分法得到梯度下降迭代方程，通过迭代演化得到极小值，从而得到图像分割结果。

2　相关背景知识

2.1测地线模型

测地线活动轮廓模型[3]是利用黎曼空间中测地线的概念，将寻找图像中目标边界的问题转化为寻找一条加权弧长最小值的问题。

令Ω⊂R2为图像区域，I:Ω→R为输入图像，C(q)为封闭轮廓区域的轮廓曲线，则测地线模型[6]即为极小化以下能量泛函：

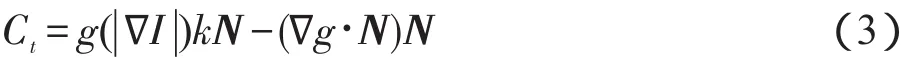
其中，k是轮廓曲线的曲率；N是轮廓曲线的内部法向量。通常增加一个恒速度项α来提高轮廓曲线演化的扩散速度，故方程（3）可写为:

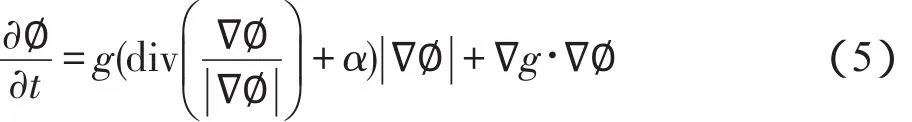
其中，α是气球力，用来控制轮廓曲线的收缩和扩张。

2.2RSF模型

为了处理活动轮廓模型中的灰度不均问题，Li等人[4,9]提出了RSF模型。给定图像区域I:Ω⊂R2→R，C为在图像区域中的封闭轮廓曲线，它将图像区域分为两部分Ω1=inside(C)和Ω2=outside(C)，具体能量泛函表示如下：

其中，λ1,λ2>0为调优参数，用以平衡两项所占的比重；f1(x)和 f2(x)分别用来估计在图像子区域Ω1、Ω2中图像强度的两个值； ||C为轮廓曲线的长度；距离正则化项定义为：

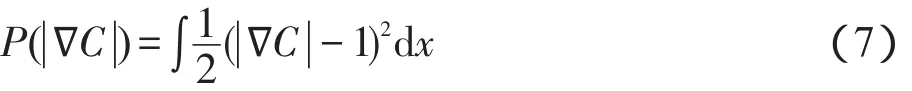
泛函中非负核函数K在[0,+∞)上满足如下性质：

在RSF模型中，核函数K取标准差为σ的高斯核函数，具体定义为：

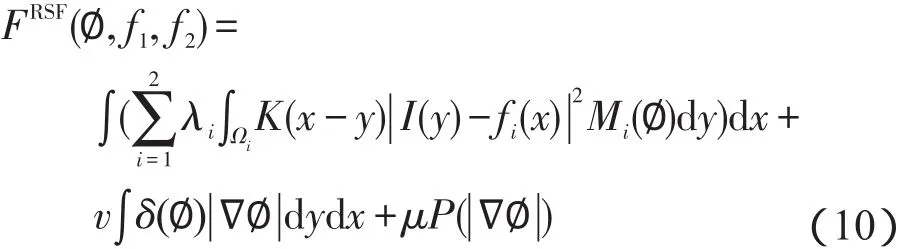
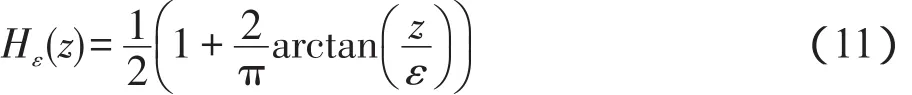
其一阶导数为：

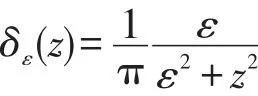
为使能量泛函达到极小，关于 f1(x)和 f2(x)分别求偏导并令其等于0，即得：而关于极小化可得到如下的梯度下降流方程：其中e1和e2函数定义为：

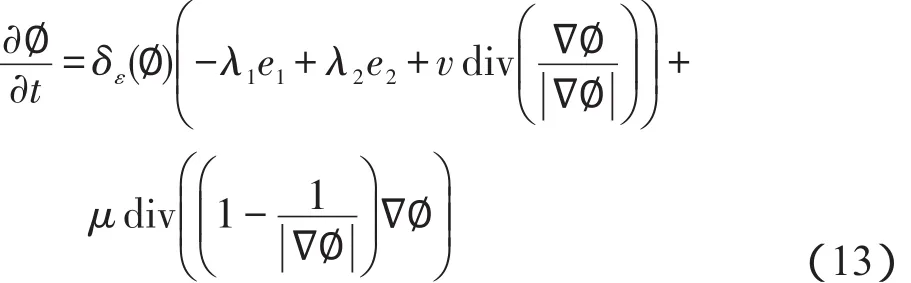
3　局部信息熵的快速混合测地区域活动轮廓模型

针对变分水平集算法在图像分割过程中计算量较大且收敛速度慢的现象，本文提出了一种新的基于区域的活动轮廓图像分割模型——局部信息熵的混合测地区域活动轮廓模型，下面具体介绍算法。

3.1局部信息熵

本文在空间连续的局部区域中定义局部信息熵。对于一幅图像I:Ω⊂R2和一个固定的规则区域Ωx⊂Ω（例如，一个以点x∈Ω为中心的邻域），点x的局部信息熵定义为：

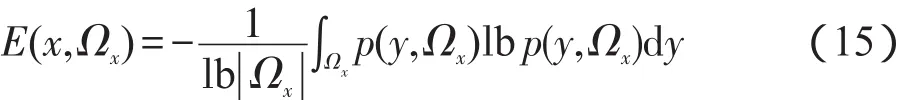
其中灰度级分布p(y,Ωx)为：

通常，邻域中局部信息熵和强度变化有关。例如，在均匀区域中局部信息熵很大，而在异质区域中局部信息熵很小。因此，当点x在（异质或噪声）匀质区域中时，点x处局部熵很大（很小）。

3.2局部信息熵的快速混合测地区域活动轮廓模型

令Ω⊂R2为图像区域，I:Ω→R为输入图像，将封闭轮廓曲线C用高一维水平集表示为C={(x,y)∈。将区域Ω划分为一些不相交的图像区域

b和c分别表示由图像构成的变化缓慢的偏移场和图像区域的灰度强度的均值向量(c1,c2)[13]，于是保证轮廓曲线向边缘收敛的数据拟合能量泛函可定义如下：

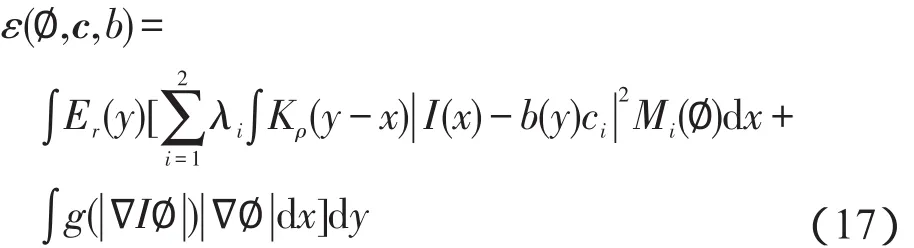
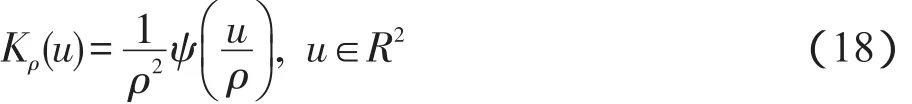
该正则化项可以更好地保持匀质区域的几何形状，防止边缘和成员函数过平滑，也可以减弱H(∙)函数在计算过程中造成的目标轮廓模糊现象。而为了避免水平集函数在演化过程中需要重新初始化水平集，在能量泛函中引入以下距离正则化项[12]：

这样，本文所研究的能量泛函可表示为：

通过求解上述能量泛函的极小值实现对图像中目标区域的分割。

3.3模型求解

能量泛函模型（22）的求解分以下3个步骤：

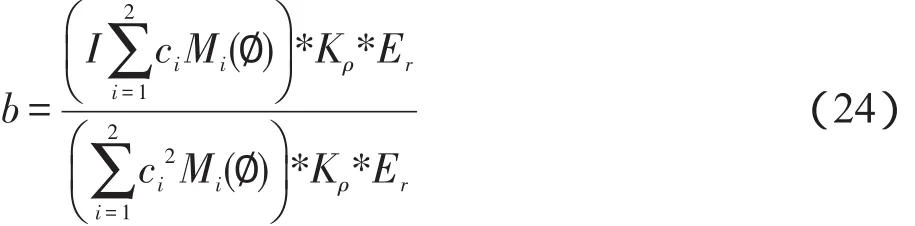
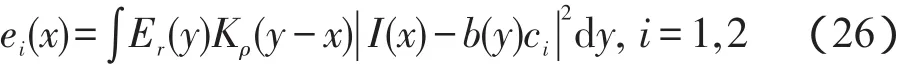
其中它也可以表示为：

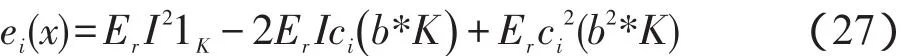
它可看作轮廓曲线指针，并满足以下边缘保持假设：

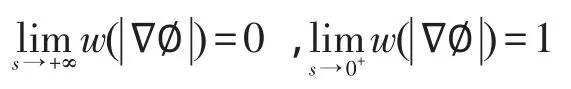
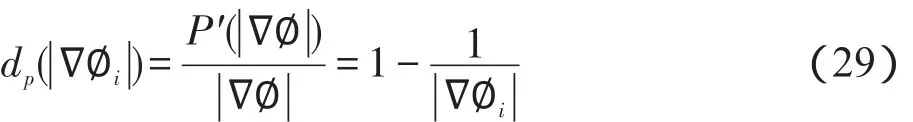
对于测地数据项，构造以下SPF函数并替代边缘检测函数g，具体函数定义如下：

其中c1与c2的定义同式（23）。该函数的取值范围为[-1,1]，它能调节目标区域内外压力的符号，从而使轮廓曲线在区域外时向内收缩，而轮廓曲线在区域内时向外扩张。

于是，梯度下降方程（25）可写为：

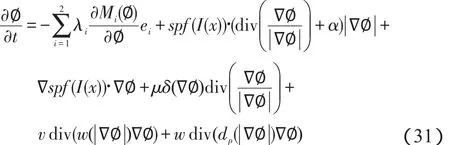
在本文HGRACM-LE算法中，水平集函数可以初始化为常量，轮廓曲线内外符号不同，这种方式在实际应用中比较容易实现。另外，基于曲率的项通常用来正则化水平集函数。因为是一个符号距离函数（sign distance function，SDF），它满足=1，所以上述正则化曲率项可以写为，它表示对水平集函数做拉普拉斯运算。根据文献[21]和文献[22]中的scale-space理论，函数演化的拉普拉斯运算等价于对函数初始化情况做高斯滤波运算，因此可以用一个高斯滤波过程替代正则化过程，而高斯函数的标准差可以用来控制正则化强度。因此，水平集函数的梯度下降流方程可以简化为：令，则使用有限差分法离散化，

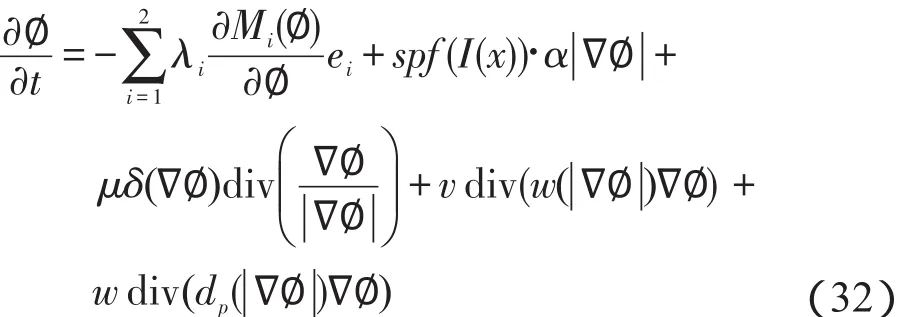
求解上述方程的梯度下降流得：

轮廓曲线在边界处满足Neumann边界条件。

综上所述，具体算法计算流程如下。

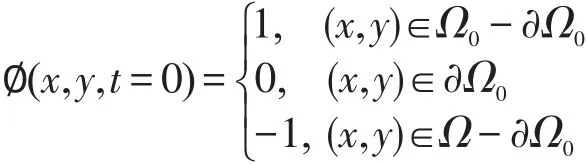
其中Ω0为图像区域Ω的子区域，初始化水平集轮廓

曲线的内部区域。

（2）根据式（23）和（24）计算c1、c2、b。

（3）根据式（30）在图像区域中计算spf函数的值。

（4）根据式（33）迭代演化水平集函数。

（6）验证迭代终止条件是否满足。如满足，则停止迭代；否则，转步骤（2）。

在步骤（5）中，高斯滤波函数Gσ的标准差σ是一个重要的参数，根据不同图像需要做出适当选择。如果σ太小，算法将会对噪声敏感，轮廓曲线的演化会不稳定；如果σ太大，可能会遇到边界遗漏情况，使检测到的目标边界不准确。在实验中，为了提高效率，将高斯核截取为K×K的掩膜函数，通常K的取值小于6。σ的一般取值范围为0.1到5。

4　实验结果与分析

本文通过一系列仿真实验来验证HGRACM-LE算法的有效性，并将实验结果和RSF模型实验结果做了对比分析。所有实验的硬件运行环境为Intel®CoreTM2 Duo CPU 3 GB内存，软件环境为Matlab R2012b搭载在Windows7旗舰版操作系统上。

Fig.1　Segmentation results of HGRACM-LE algorithm and RSF model for different images图1HGRACM-LE算法和RSF模型算法对不同图像的分割结果

第一组实验选了3幅图像，如图1所示。其中图像1为84×84像素的bmp压缩格式的合成图像，图像2和图像3分别为200×200像素和180×132像素的bmp压缩格式和jpg压缩格式的真实图像。实验参数为：，其中α依次分别为0.01,15,0.5，高斯滤波函数为方差σ依次取1.5,0.3,0.6的5×5的滤波矩阵。图1（a）为图像的初始轮廓曲线形状和位置；图1（b）为对应图1（a）初始化轮廓曲线RSF模型算法迭代计算80次、300次及240；图1（c）为对应图1（a）初始化轮廓曲线HGRACM-LE算法迭代2次的分割结果。由图像分割结果对比可知，本文提出的算法可以更准确地分割出目标图像，没有多余的演化曲线表1是对应1仿真实验两种算法的CPU。从数据对比可知，本文HGRACM-LE算法收敛较快，分割出图像所需要的时间较短。

第二组实验如图2所示，实验所选图像为png压缩格式的大小为400×320像素的真实图像，该图像由于光照条件影响，图像灰度强度明显分布不均匀。实验所选参数为w=1,α=1,λ1=λ2=1,μ=0.005× 2552,v=0.01,1,1，高斯滤波函数为方差σ依次为1.5,4,2.5,1的5×5的滤波矩阵。图2（a）为图像中的初始轮廓曲线位置；图2（b）为对应图2（a）初始位置RSF模型算法在轮廓曲线迭代100次以后的分割结果；图2（c）为对应图2（a）初始化位置本文HGRACMLE算法在轮廓曲线迭代4次后的分割结果。由图像分割结果对比可知，本文提出的HGRACM-LE算法分割出的目标图像更为准确，没有多余的环状演化曲线。而表2是RSF模型和HGRACM-LE算法在不同初始化位置相应的CPU耗时。由表2不难看出，HGRACM-LE算法较RSF模型算法分割收敛速度更快。

Table 1　CPU time of RSF model and HGRACM-LE algorithm to segment image in different initial contours表1RSF模型和HGRACM-LE算法对不同图像分割结果的CPU耗时

图2　HGRACM-LE算法和RSF模型算法在不同轮廓曲线初始位置时对灰度不均匀图像的分割结果

Table 2　CPU time of RSF model and HGRACM-LE algorithm to segment the image in different initial contours表2RSF模型和HGRACM-LE算法在初始位置不同时分割图像CPU耗时　s

Fig.3　Segmentation results of HGRACM-LE algorithm with differentσin Gaussian filter function图3HGRACM-LE算法在高斯滤波函数中σ不同取值时图像分割结果

第三组实验如图3所示，所选图像为bmp压缩格式的医学中的核磁共振图像，大小为256×256像素。本实验主要讨论算法计算过程中步骤（5）高斯滤波函数对分割结果的影响。实验所选参数为λ1=λ2=1.5,μ=0.005×2552,v=w=1,α=1，高斯滤波函数为5×5的滤波矩阵。图3中图（a）为初始化轮廓曲线，图（b）~（i）分别为高斯滤波函数标准差σ=0.01,0.1,1,3,5,7,10,15时对应（a）所示轮廓曲线在迭代计算8次的图像分割结果。从实验分割结果来看，当σ取值较小时（如（b）（c）所示），可以取得较为精细的分割结果，但是会受一些噪声点的影响；当σ取较大值时，分割结果受噪声影响较小，但是分割结果不够精确；当σ>5时，分割结果接近相同，说明此时高斯滤波函数已经失去了平滑图像噪声的作用，对分割结果几乎不产生影响。因此，σ的取值范围一般控制在(0,5]之间，根据具体图像选择合适的值。

综上可知，本文HGRACM-LE算法可以有效地处理灰度不均图像，且算法对轮廓曲线的初始位置不敏感，分割准确性较高，速度也较快。

5　结束语

本文提出了一种基于局部信息熵的快速混合测地区域活动轮廓模型的图像分割算法。本文算法使用双图像拟合项，并构造了新的SPF函数来代替边缘检测函数，以高斯滤波代替拉普拉斯运算，从而降低了迭代计算的复杂度，可以加速轮廓曲线的收敛速度，从而减少分割所需的时间。另外，算法引入柔化核函数作为窗口核函数对图像能量拟合项进行平滑，同时通过非凸函数对水平集函数进行正则化，使得函数在演化过程中保持理想的形状。从实验结果可以看出，本文算法在处理灰度不均匀图像时也取得了较好的分割效果，且对初始轮廓曲线的位置不敏感，具有很好的稳定性。

References:

[1]Aubert G,Kornprobst P.Mathematical problems in image processing:partial differential equations and the calculus of variations[M].[S.l.]:Springer Science&Business Media, 2006.

[2]Kass M,Witkin A,Terzopoulos D.Snakes:active contour models[J].International Journal of Computer Vision,1988, 1(4):321-331.

[3]Caselles V,Kimmel R,Sapiro G.Geodesic active contours[J]. International Journal of Computer Vision,1997,22(1):61-79.

[4]Li Chunming,Kao CY,Gore J C,et al.Minimization of regionscalable fitting energy for image segmentation[J].IEEE Transactions on Image Processing,2008,17(10):1940-1949.

[5]Zhang Jianwei,Ma Xiang,Chen Yunjie,et al.MR image segmentation based on local information entropy geodesic active contour model[J].International Journal of Multimedia and Ubiquitous Engineering,2014,9(4):127-136.

[6]Mumford D,Shah J.Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on Pure and Applied Mathematics,1989, 42(5):577-685.

[7]Chan T F,Vese L A.Active contours without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.

[8]Li Chunming,Xu Chenyang,Gui Changfeng,et al.Level set evolution without re-initialization:a new variational formulation[C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,San Diego,USA,Jun 20-26,2005.Washington:IEEE Computer Society,2005,1:430-436.

[9]Li Chunming,Kao C Y,Gore J C,et al.Implicit active contours driven by local binary fitting energy[C]//Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition,Minneapolis,USA,Jun 18-23,2007.Washington:IEEE Computer Society,2007:1-7.

[10]Zhang Kaihua,Zhang Lei,Song Huihui,et al.Active contours with selective local or global segmentation:a new formulation and level set method[J].Image and Vision Computing, 2010,28(4):668-676.

[11]He Chuanjiang,Wang Yan,Chen Qiang.Active contours driven by weighted region-scalable fitting energy based on local entropy[J].Signal Processing,2012,92(2):587-600.

[12]Li Chunming,Xu Chenyang,Gui Changfeng,et al.Distance regularized level set evolution and its application to image segmentation[J].IEEE Transactions on Image Processing,2010,19(12):3243-3254.

[13]Li Chunming,Huang Rui,Ding Zhaohua,et al.A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J].IEEE Transactions on Image Processing,2011,20(7):2007-2016.

[14]Lankton S,Nain D,Yezzi A,et al.Hybrid geodesic regionbased curve evolutions for image segmentation[C]//SPIE 6510:Medical Imaging 2007,Physics of Medical Imaging,San Diego,USA,Feb 17-22,2007.[S.l.]:International Society for Optics and Photonics,2007.

[15]Han Yu,Wang Weiwei,Feng Xiangchu.A new fast multiphase image segmentation algorithm based on nonconvex regularizer[J].Pattern Recognition,2012,45(1):363-372.

[16]Xu Haiyong,Liu Tingting,Wang Guotao.Hybrid geodesic region-based active contours for image segmentation[J]. Computers&Electrical Engineering,2014,40(3):858-869.

[17]Peng Yali,Liu Fang,Liu Shigang.Active contours driven by normalized local image fitting energy[J].Concurrency and Computation:Practice and Experience,2014,26(5):1200-1214.

[18]Frieden B R.Restoring with maximum likelihood and maximum entropy[J].Journal of the Optical Society of America, 1972,62(4):511-518.

[19]Sezgin M.Survey over image thresholding techniques and quantitative performance evaluation[J].Journal of Electronic Imaging,2004,13(1):146-168.

[20]Shiozaki A.Edge extraction using entropy operator[J]. Computer Vision,Graphics,and Image Processing,1986,36 (1):1-9.

[21]Shi Y,Karl W C.Real-time tracking using level sets[C]// Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,San Diego,USA,Jun 20-26,2005.Washington:IEEE Computer Society,2005,2:34-41.

[22]Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

LIN Xilan was born in 1989.She is an M.S.candidate at Jiangnan University,the student member of CCF.Her research interests include digital image processing and image segmentation,etc.

林喜兰（1989—），女，河南新乡人，江南大学硕士研究生，CCF学生会员，主要研究领域为数字图像处理，图像分割等。

CHEN Xiuhong was born in 1964.He received the Ph.D.degree in applied mathematics from East China University of Science and Technology in 2000.During 2001 to 2006,he was doing postdoctoral research work successively at Nanjing University and Nanjing University of Science and Technology.Now he is a professor at Jiangnan University. His research interests include digital image processing,pattern recognition,artificial intelligence and moving targets tracking,etc.

陈秀宏（1964—），男，江苏泰州人，2000年于华东理工大学获得博士学位，2001—2006年在南京大学和南京理工大学从事博士后研究工作，现为江南大学数字媒体学院教授，主要研究领域为数字图像处理，模式识别，人工智能，运动目标跟踪等。在专业杂志发表学术论文逾100篇，参加国家自然科学基金项目3项，江苏省自然科学基金项目1项，主持省部级研究项目3项，省博士后基金项目1项，横向科研项目若干。

XIAO Linyun was born in 1988.He is an M.S.candidate at Jiangnan University.His research interest is digital image processing.

肖林云（1988—），男，湖南邵阳人，江南大学硕士研究生，主要研究领域为数字图像处理。

Fast Hybrid Geodesic Region Active Contour Model of Local Entropy*

LIN Xilan+,CHEN Xiuhong,XIAO Linyun
School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:linxilanjn@163.com

LIN Xilan,CHEN Xiuhong,XIAO Linyun.Fast hybrid geodesic region active contour model of local entropy. Journal of Frontiers of Computer Science and Technology,2016,10(9):1332-1340.

Aiming at the phenomenon that the variational level set algorithm takes large amount of calculation and converges slowly in the process of image segmentation,this paper proposes a new hybrid geodesic region active contour model of local entropy based on the predecessors’research.The model constructs a new energy functional,introduces a mollifying kernel function to be window function,constructs a new signed pressure force function to replace the geodesic edge stopping function,and uses local entropy as the weight of image fitting energy,then adds a nonconvex regularization term to constrain the level set function.The algorithm getting from this not only accelerates the convergence rate of the contour curve,but also can address image segmentation inaccuracy for image intensity inhomogeneity or blurring caused by the change of illumination or other external factors.The simulation experiment results on synthetic images and real images show that the proposed algorithm is of higher converging speed and better accuracy,less sensitive to the location of initial contour at the same time,and has better robustness.

hybrid geodesic region active contour model;mollifying kernel function;signed pressure force function;local entropy;nonconvex regularization term

*The National Natural Science Foundation of China under Grant No.61373055(国家自然科学基金). Received 2015-06,Accepted 2015-08.

CNKI网络优先出版:2015-09-06,http://www.cnki.net/kcms/detail/11.5602.TP.20150906.1556.008.html

A

TP391.4