一种新型相移场探头改变导体涡电流分布的理论验证*

张思全，唐江锋

（上海海事大学电气自动化系，上海，201306）

一种新型相移场探头改变导体涡电流分布的理论验证*

张思全*，唐江锋

（上海海事大学电气自动化系，上海，201306）

涡流检测方法广泛应用于导电材料的缺陷检测和无损评价中。受趋肤效应的影响，常规涡流检测法通常只能检测导体表面缺陷。有学者提出了一种相移场探头，并通过实验验证了该探头在满足一定激励条件时，可以达到抑制导体表面涡电流密度，而增加导体深处涡电流密度的效果，从而可以检测导体更深处缺陷。但该结论仅有实验结果，还没有理论方面的验证。本文采用解析方法研究了该相移探头与导体的相互作用，推导出导体中涡电流分布的精确理论表达式，然后分析相位、激励频率对涡电流分布的影响，并计算了导体不同深度涡电流密度分布。从理论上验证了该探头设计及激励方法具有改变导体涡电流密度分布，增加导体深处涡电流密度的效果。

涡流检测；渗透深度；解析计算；相移场探头；涡电流分布

涡流检测技术广泛应用于工业各个领域关键部件的安全评价，与超声等其他检测方法相比，涡流检测法具有对导电结构表面、亚表面缺陷检测灵敏度高、操作简单等多种优势。在传统涡流检测中，一个通电圆柱线圈作为激励探头，线圈中交变电流产生变化的磁场，与导体进行交互作用并在导体中产生感应涡电流。如果导体表面有缺陷，则涡电流流过缺陷时，流动方向会发生变化，并产生与无缺陷情况下不同的反射磁场，反射磁场作用到检测线圈上会造成线圈阻抗或感应电压的变化，通过测量检测线圈中阻抗或感应电压的变化可以进行缺陷检测与形状重构，这是常规电磁无损检测方法进行缺陷检测与定量的原理［1-4］。然而，受趋肤效应的影响，在导电材料内部，涡电流密度随深度增加按指数衰减，衰减后的涡电流与导体深处缺陷相互作用产生的信号非常微弱难以被检测到。因此涡流法主要适用于检测深度小于5mm的缺陷。虽然出现了一些采用脉冲涡流法或超导量子干涉设备SQUID（Superconducting Quantum Interference Device）等新方法［5-6］，但这些方法通常比常规涡电流方法复杂且难以应用。

为此，很多学者在如何提高常规涡电流渗透深度方面进行了大量研究。这些工作主要集中在对涡流探头结构设计和激励方式的改进方面［7-8］。近年来，有学者提出了一种新型相移场探头，该探头由四个相互平行且垂直于导体表面的矩形激励线圈和一个平行于导体表面的圆柱采集线圈组成。四个激励线圈分为内外两组，可以通过不同接线方法进行线圈匝数和激励方式的变化［9-10］。文献作者通过实验得到结论：如果两个内部激励线圈与两个外部激励线圈有180度的电流相位差，可以使叠加形成的涡电流分布在导体深度方向上形成非指数性衰减，达到减小导体表面涡电流密度且增加深层涡电流密度的效果，从而可以检测导体内部深层缺陷。但该结论仅通过实验得到，还没有相关的理论验证［11］。本文探讨利用解析方法验证该结论。

1　理论分析

1.1解析模型

图1（a）所示为一个单匝矩形线圈位于多层导电平板上方。导电平板表面与z=0平面重合。矩形线圈平行于x、z轴，垂直于y轴，边长分别是2a0和2b0，线圈所在平面与z轴的距离是c，线圈中心距导体表面的距离是z0。线圈中通有正弦激励电流Iejωt，I为电流幅值，ω为角频率。导体为线性、均匀和各向同性材料。假设上层导体的厚度、电导率和磁导率分别为d、μ1和σ1，下层导体的电导率和磁导率分别为μ2和σ2，厚度为无限。图1（b）所示为由图1（a）单匝矩形线圈分别向y轴正、负方向各扩展h/2、沿四个边向外扩展w而形成的多匝线圈。

为分析方便，将整个空间分为三个区域：

区域0：在z＞0范围，同时存在激励电流产生的入射磁通量密度Bi和导体中感应涡电流产生的反射磁通量密度Br。

区域1：在-d＜z＜0范围，是上层导电平板，存在磁通量密度B1。

区域2：在z＜-d范围，是下层导体区域，存在磁通量密度B2。

为求解各区域的电磁场方程，引入如下二维傅立叶变换及其逆变换：

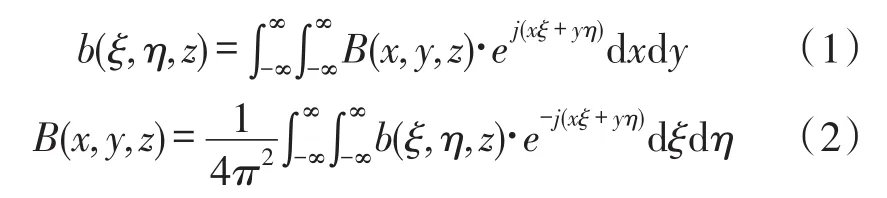
式中ξ和η是二维傅立叶变换中的积分变量。

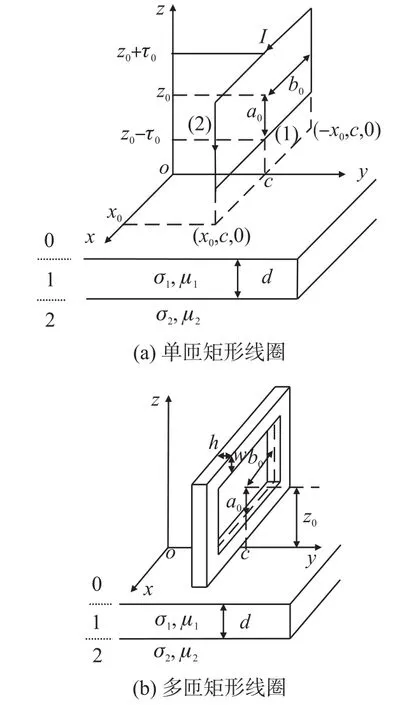
图1　矩形线圈位于多层导体上方

1.2导电平板区域磁通量密度

按照文献［12，13］中的方法，可以得到图1（a）中单匝矩形线圈在区域0产生的入射磁通量密度的z分量为：

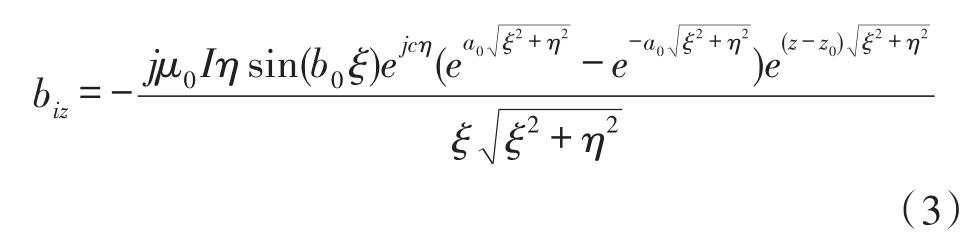
根据各区域电磁场激励与反射的特征，可以设定各区域的磁通量密度各分量通解。区域0：

区域1：

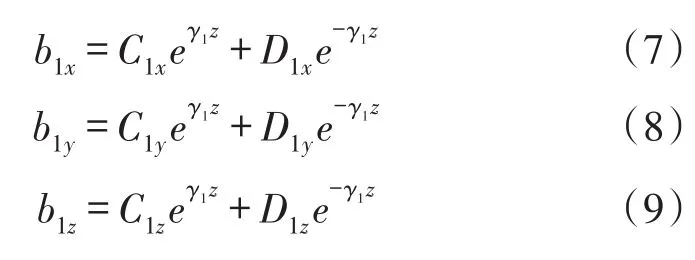
式中

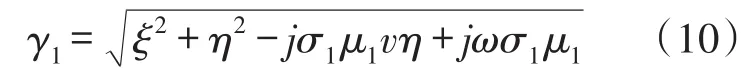
区域2：

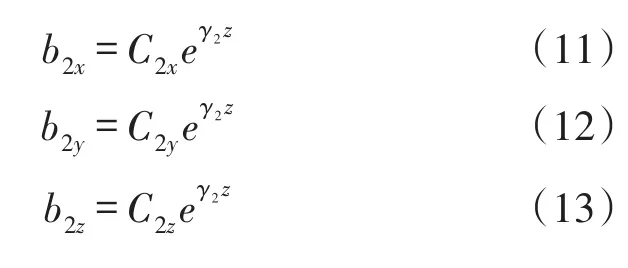
式中

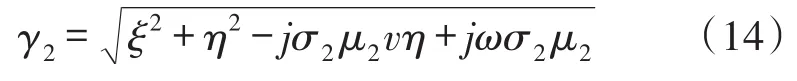
根据式（6），可得到图1（a）中单匝矩形线圈产生的入射磁通量密度z分量的系数如下：

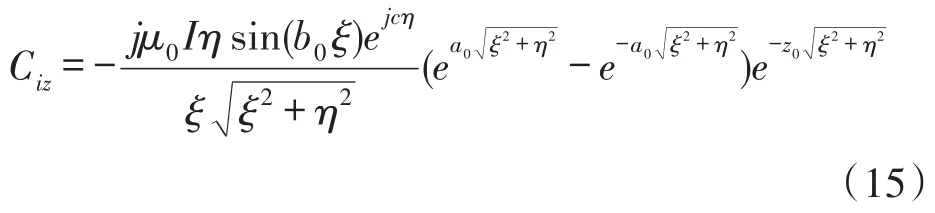
为求解各区域磁通量密度的通解，利用B的垂直分量和H的切向分量在平面z=0和z=-d连续的特性构建方程组。在求解过程中，为简化表达式，设定如下参数：

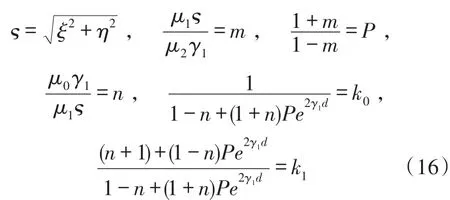
求得区域1中的磁通量密度各系数如下：

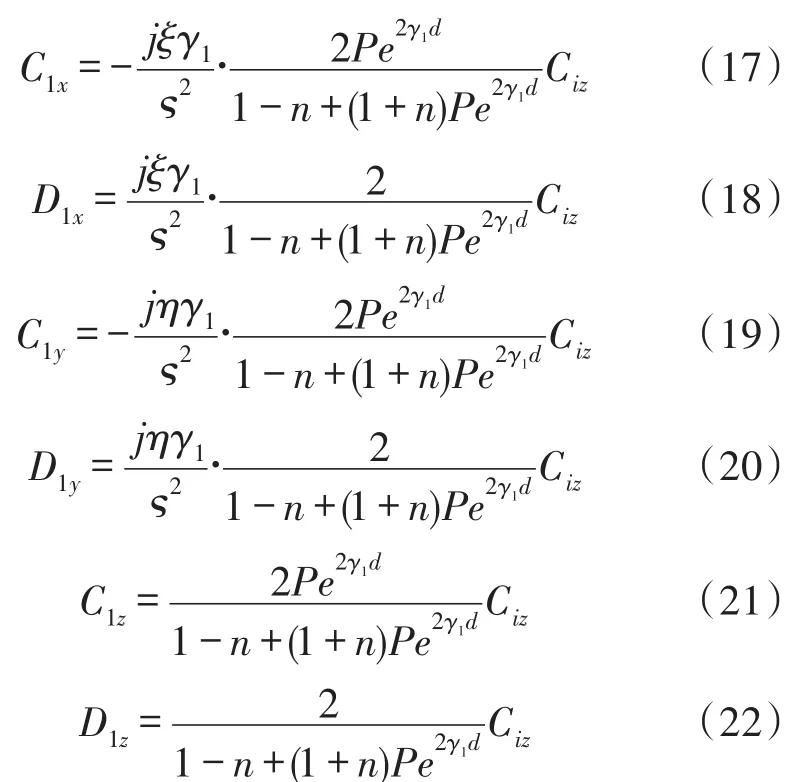
可得区域1中的磁通量密度各分量如下：

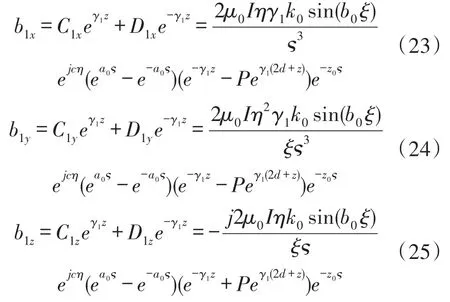
对式（23）～式（25）进行傅立叶变换，得到区域1中磁通量密度各分量如下：

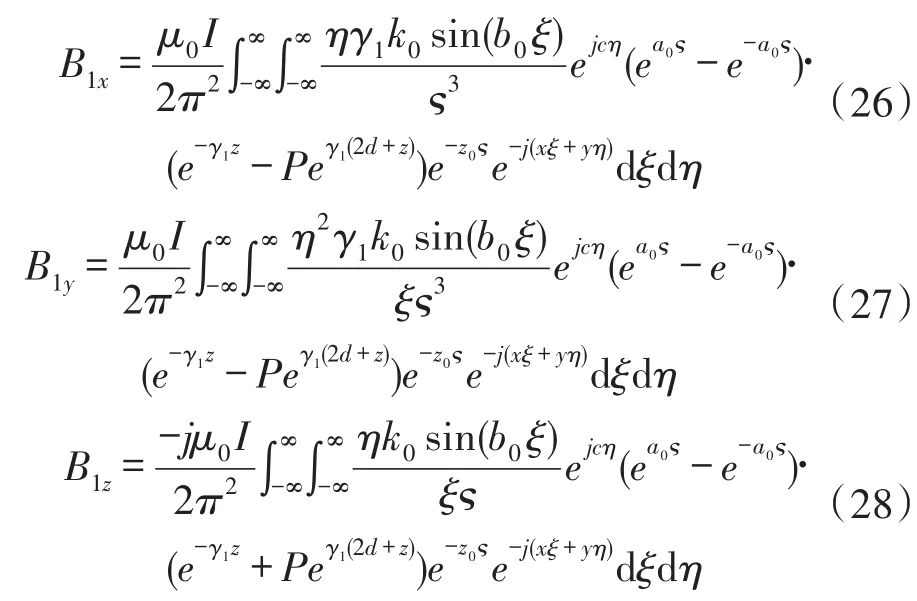
设单匝矩形线圈在y轴的位置为c，通过将式（26）～式（28）沿图1（b）所示矩形线圈的宽度和长度方向积分，可以得到多匝矩形激励线圈在平板区域产生的磁通量密度各分量如下：

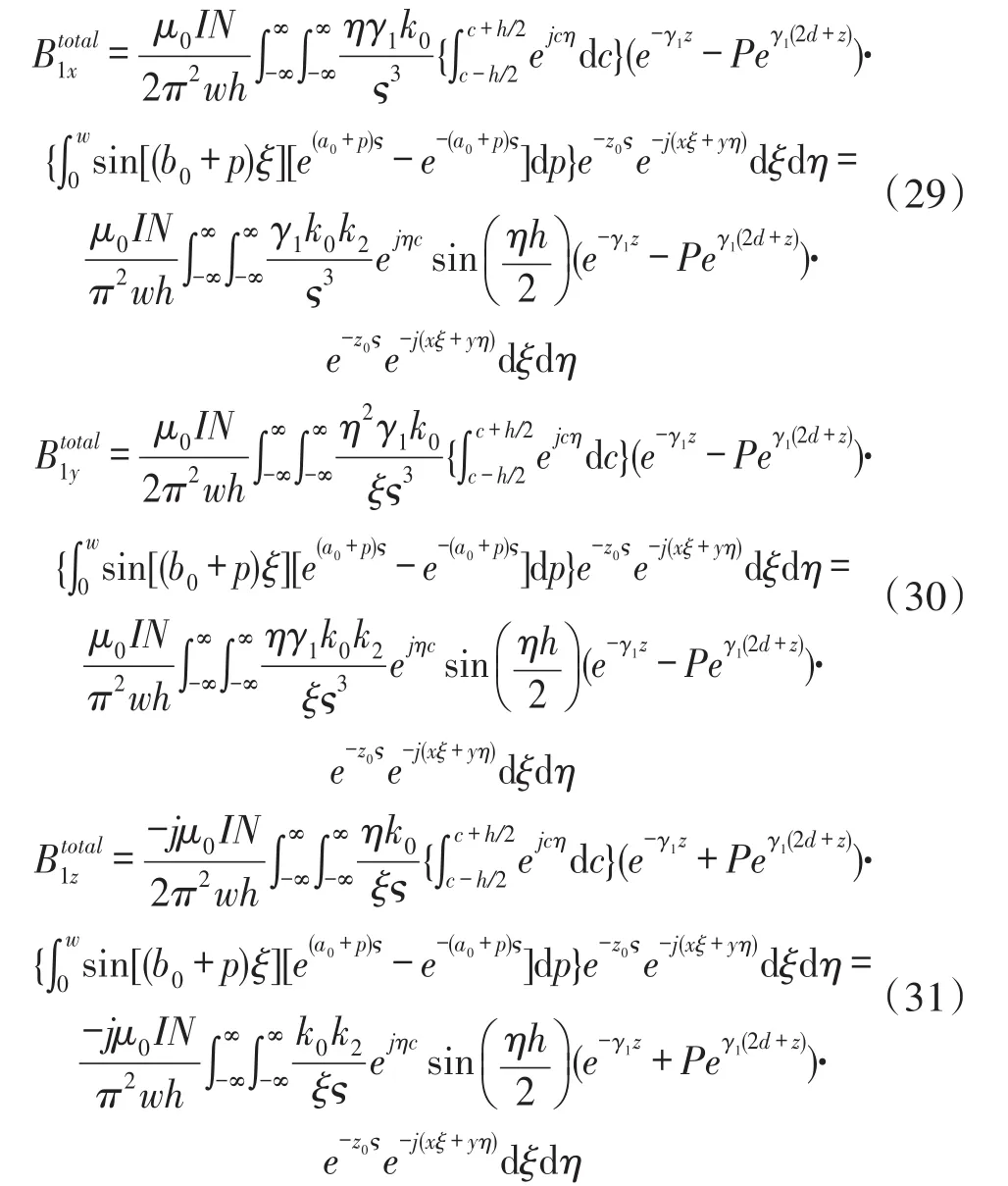
式中

2　导体中的涡电流分布

将图1（b）中的一个多匝矩形线圈扩展为4个相同多匝矩形线圈，构成如图2所示相移场探头激励系统。其中四个矩形激励线圈，编号分别为1、2、3、4，其中线圈1、4称为外部线圈，线圈2、3称为内部线圈。设四个线圈中心对应于y轴上的位置分别为c1、c2、c3、c4。

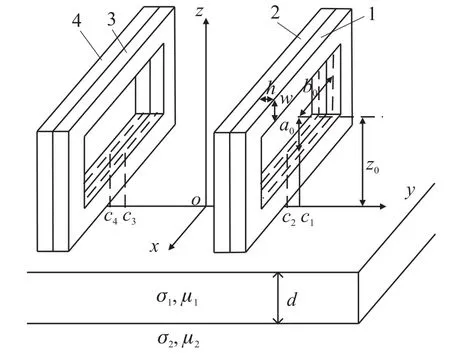
图2　构成相移场探头的四个多匝矩形激励线圈

由计算得到的导体中的磁通量密度各分量，可以进一步如下计算导体中涡电流的x和y分量：

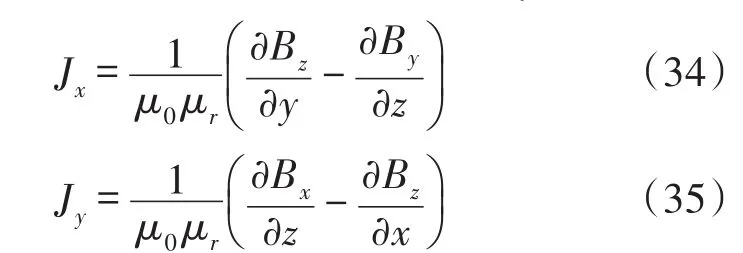
对于图2中所示线圈1，2，3和4，可以分别得到其单独激励下在导体中产生的涡电流各分量：

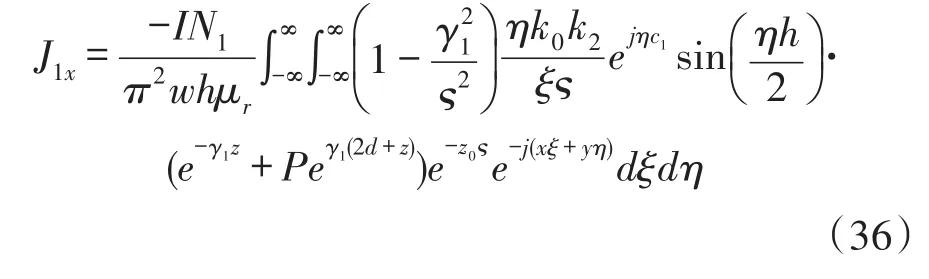
3　结果

按照前面部分得到的式（36）～式（43），计算由相移场探头在导体中产生的感应涡电流。导体中的涡电流由线圈1、2、3和4各自产生的涡电流叠加而形成。探头线圈和导体参数分别由表1和表2给定。按给定参数可以计算出导体的渗透深度为1.82mm。为了验证所提出相移场探头的特性，给其施加不同激励参数以比较不同导体深度的涡电流分布。

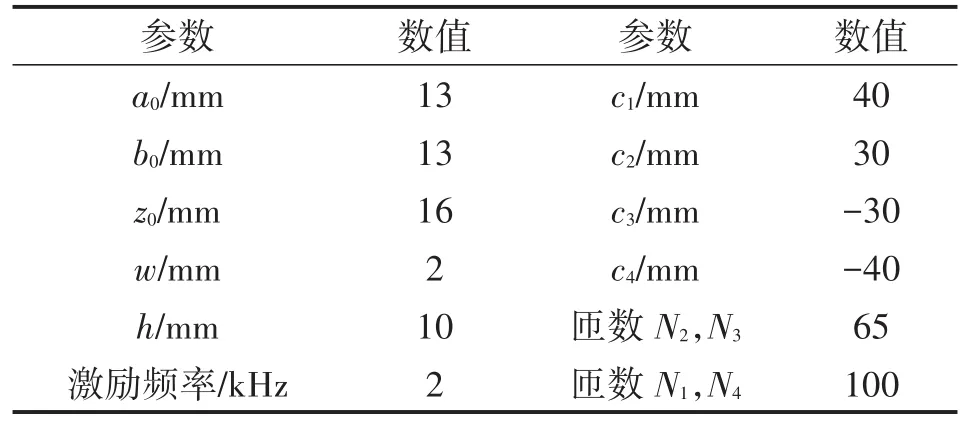
表1　相移场探头激励线圈参数

表2　导体参数

3.1内外线圈施加同相激励电流

给外部线圈1、4施加相同方向及相位的激励电流，同时给内部线圈2、3施加与外部线圈相同的激励电流。在这样的激励方式下，相移场探头相当于常规涡电流探头。此时，导体中总的涡电流密度为：

其中，涡电流的x和y分量是四个相同激励电流矩形线圈产生涡电流的叠加：

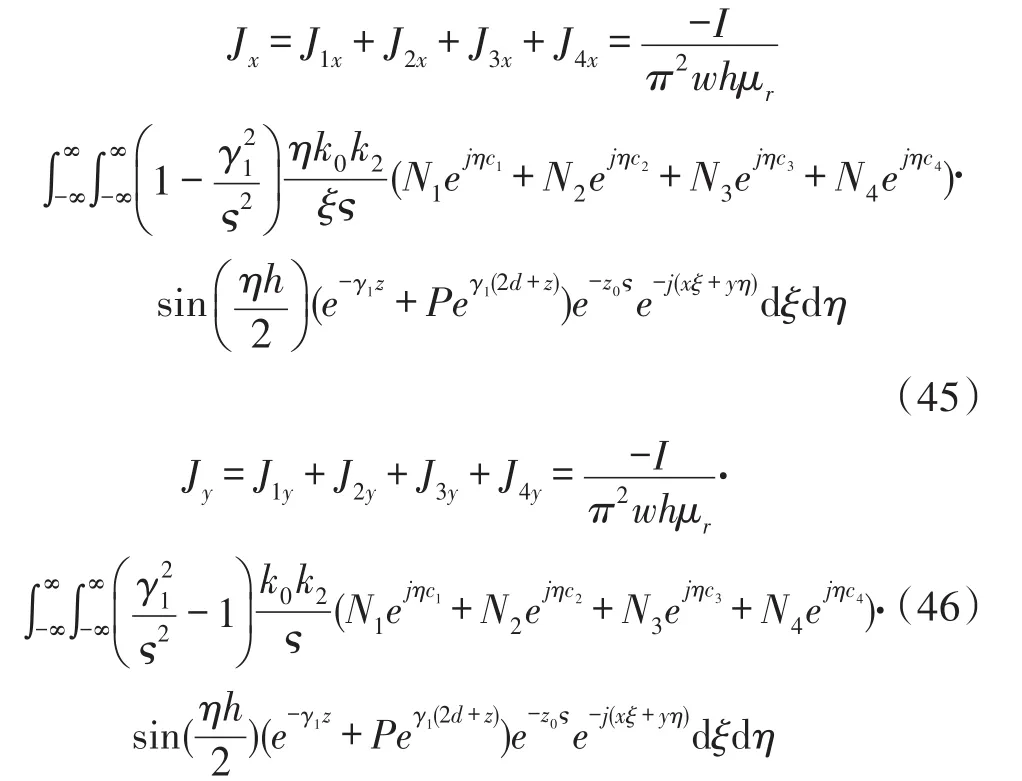
3.2内外线圈施加反相激励电流

文献［11］所提出相移场探头，其实验能够取得较深涡电流渗透深度的原因在于内、外线圈激励电流相位相差180°。因此，给外部线圈1、4施加相同方向的激励电流，给内部线圈2、3施加与外部线圈相反方向的激励电流。此时，导体中总的涡电流密度为：

其中，涡电流的x和y分量是内外线圈在不同方向电流激励下产生涡电流的叠加：

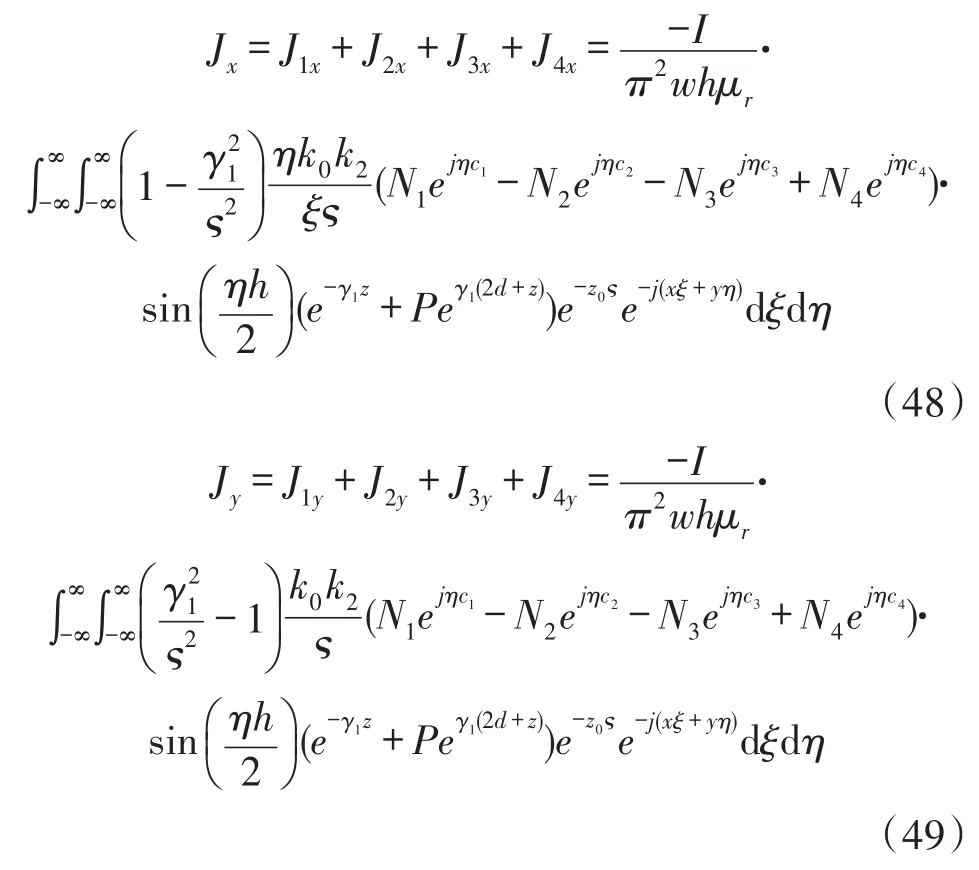
图3所示为激励线圈在导体表面产生的涡电流分布，线圈激励频率为f=2 kHz，线圈匝数按参考文献［12］设为外线圈N1=N4=100，内线圈N2=N3=65。计算所得涡电流密度值仅具有相对比较意义，其数值会随着参数变化而不同。由图3（a）可见，在内外线圈施加相同方向激励电流时，激励线圈下方及线圈之间导体表面都有涡电流存在，且线圈之间涡电流密度近似为线圈下方涡电流最大值的三分之一。由图3（b）可见，在给内外线圈施加方向相反的激励电流时，线圈之间导体表面涡电流基本消失，而线圈所在区域下方涡电流密度最大值和分布区域比3（a）都有所增大。

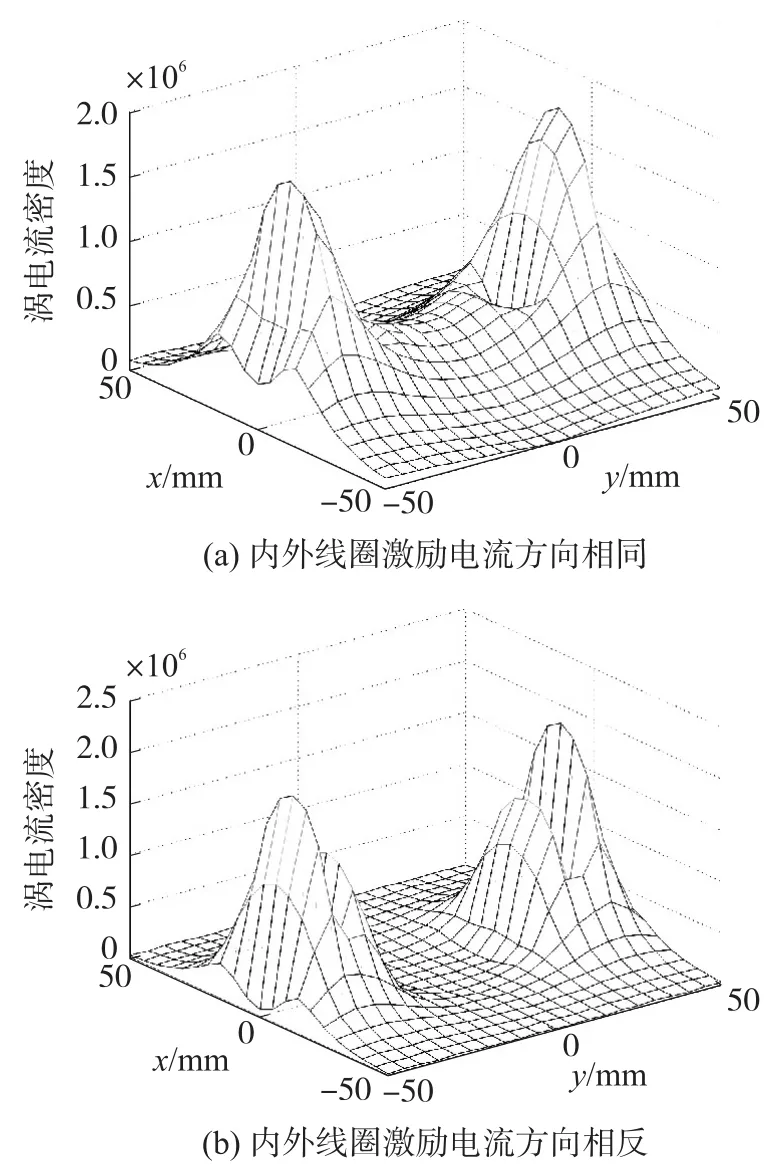
图3　涡电流分布（z=0mm，f=2 kHz）

图4所示为激励线圈在导体10mm深处产生的涡电流密度分布，电流激励频率和线圈匝数同上。由图4（a）可见，当内外线圈激励电流同向时，两组线圈中心区域存在涡电流分布，而当内外线圈被施加反相激励电流时，由图4（b）可见，线圈之间涡电流密度消失，而线圈下方涡电流密度最大值比4（a）中有明显提高，这有助于导体10mm深处缺陷的检测。

图5所示为激励线圈在导体20mm深处产生的涡电流分布，电流激励频率和各线圈匝数不变。由图5（a）可见，当内外线圈激励电流同向时，线圈之间区域20mm深处存在涡电流，且其密度接近于线圈下方最大值的三分之一。当内外线圈激励电流反向时，由图5（b）可见，线圈之间涡电流基本消失，且在线圈下方各自产生一个新的涡电流集中区域，使得线圈下方有效涡电流分布区域大于5（a）中，这有助于导体20mm深处缺陷的检测。

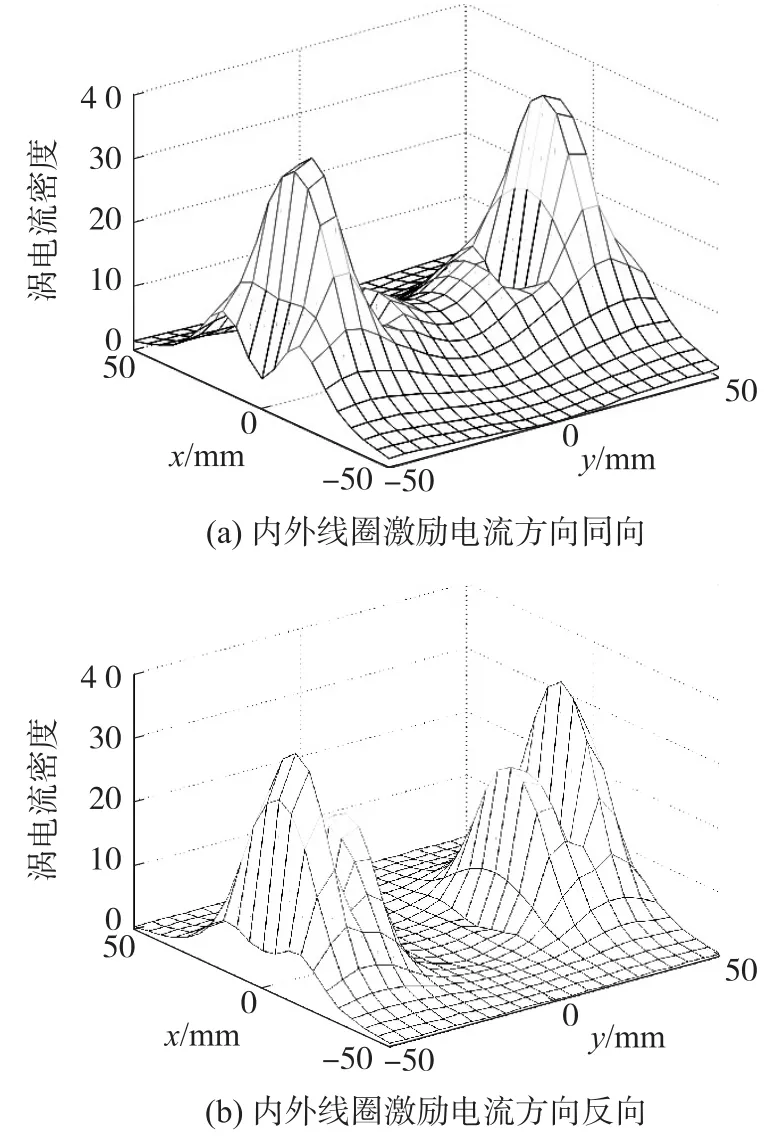
图5　涡电流分布（z=-20mm，f=2 kHz）

图6所示为激励线圈在导体30mm深处产生的感应涡电流分布，采用相同的电流激励频率和线圈匝数。由图6（a）、（b）可见，当导体深度增加到30mm时，涡电流密度已经很小，但采用内外线圈反向电流激励时，仍然可以起到减小线圈之间区域涡电流，而增大线圈下方涡电流密度及有效分布区域的作用，有利于线圈下方导体30mm深处缺陷的检测。

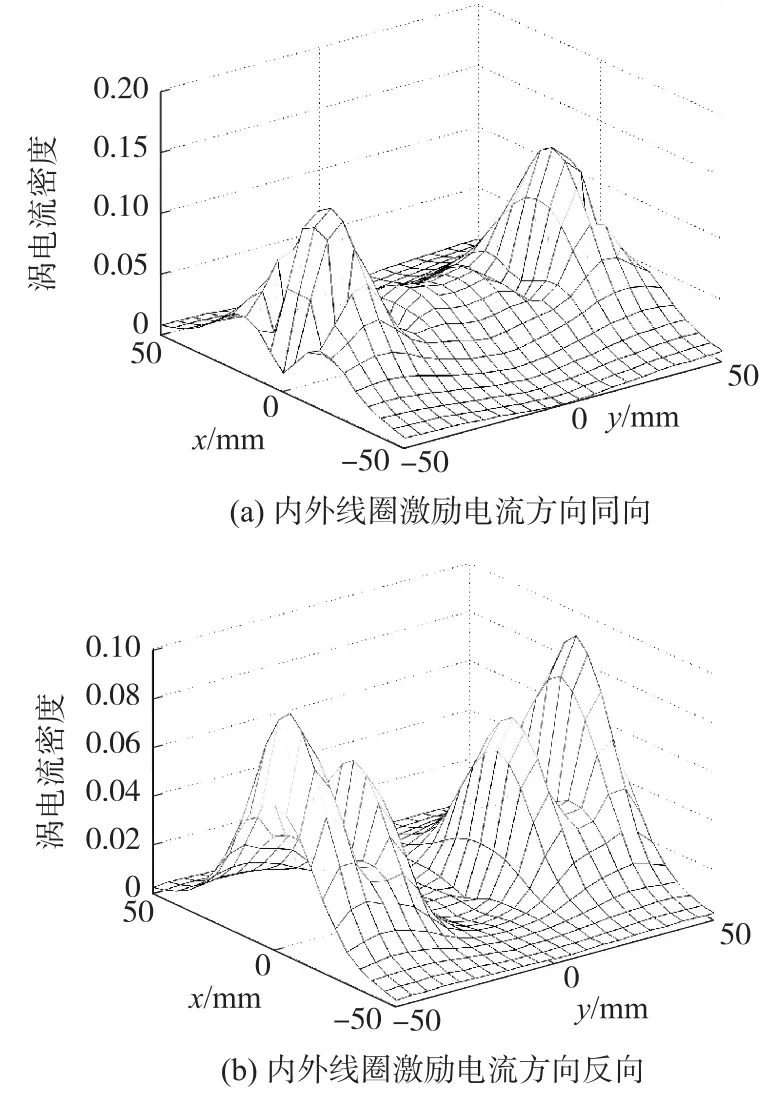
图6　涡电流分布（z=-30mm，f=2 kHz）

3.3仿真验证

利用Ansoft软件进行仿真，内部线圈匝数设为600，外部线圈匝数设为1 000，激励频率设为500 Hz。由图7（a）可见，当内部线圈与外部线圈激励电流同向时，在线圈下方及线圈之间的导体内部都有涡电流产生。其他条件不变，仅改变内部线圈与外部线圈激励电流，使其反向，得到如图7（b）的涡电流分布图。

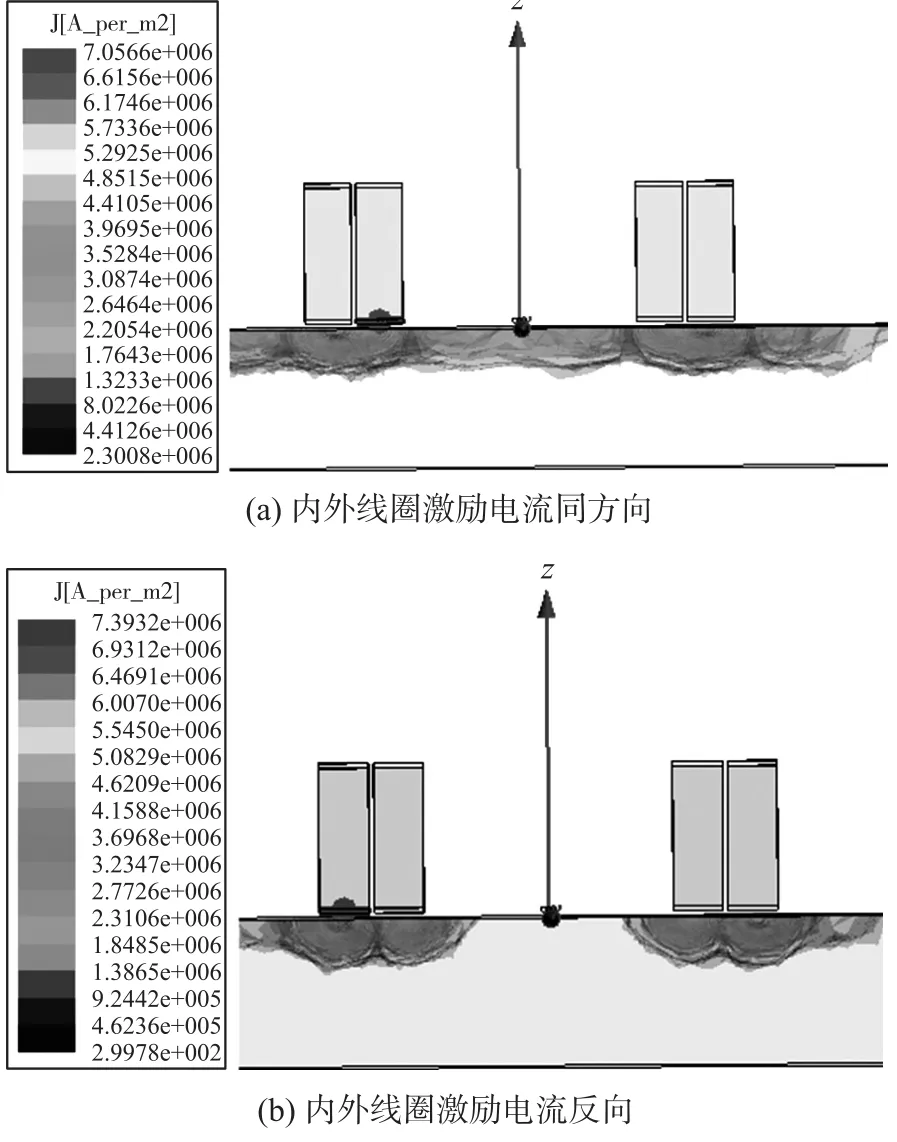
图7　仿真得到的涡电流分布（f=500 Hz）

可见线圈之间导体区域涡电流基本消失，而激励线圈下方涡流渗透深度增加。从仿真结果发现，使线圈之间导体涡电流得到抑制的关键因素是使内部线圈与外部线圈激励电流反向或相位相差180°。这与前面的解析计算结果符合，也部分验证了文献［11］中的实验结果。

4　结论

针对学者提出的一种新型相移场涡流探头，其优点在于可以改变导体中涡电流的分布，从而提高涡电流的渗透深度，达到检测导体深处缺陷的目的，但作者仅从实验上得到该结论，尚未有充分的理论验证。采用解析方法对文献中所提出的相移场探头与导体之间的相互作用进行了分析，首先导出相移场探头在导体区域激励产生的磁感应强度，

然后获得导体中涡电流分布的精确理论表达式。

分析了相位、激励频率对涡电流分布的影响，计算了导体不同深度涡电流密度分布，并以三维涡电流分布图的形式直观显示了理论推导结果，该解析计算结果表明，文献中所提出的新型相移场探头在一定激励条件下，可以改变导体表面及不同深度涡电流的分布，这验证了该探头设计与激励方法在改变导体表面涡电流密度，增加导体深处涡电流密度方面是有一定效果的。

［1］杜金强，李培源，何宇廷，等.花萼状涡流阵列传感器裂纹在线定量识别算法［J］.传感技术学报，2015，28（5）：684-689.

［2］陈国龙，张卫民，庞炜涵，等.基于科赫雪花图形激励装置的涡流传感器工作原理分析［J］.传感技术学报，2015，28（10）：1454-1458.

［3］张思全，胡盛斌，陆文华，等.任意层导电板上方线圈阻抗的级数计算模型［J］.传感技术学报，2011，24（11）：1596-1601.

［4］焦胜博，丁华，何宇廷，等.基于半解析模型的花萼状涡流传感器损伤监测灵敏度分析［J］.传感技术学报，2013，26（2）：205-210.

［5］Michniakova M，Janousek L，Smetana M.Impact of Probe Configuration on Cracks Depth Resolution in Pulsed Eddy Current Non-Destructive Evaluation［J］.Przeglad Elektrotechniczny，2012，88 （7b）：226-228.

［6］Jeng J T，Yang S Y，Horng H E，et al.Detection of Deep Flaws by Using a HTS-SQUID in Unshielded Environment［J］.Applied Superconductivity，IEEE Transactions on，2001，11（1）：1295-1298.

［7］Mook G，Hesse O，Uchanin V.Deep penetrating eddy currents and probes［J］.Materials Testing，2007，49（5）：258-264.

［8］Thollon F，Lebrun B，Burais N，et al.Numerical and Experimental Study of Eddy Current Probes in NDT of Structures with Deep Flaws［J］.NDT&E International，1995，28（2）：97-102.

［9］Janousek L，Chen Z，Yusa N，et al.Excitation with Phase Shifted Fields-Enhancing Evaluation of Deep Cracks in Eddy-Current Testing［J］.NDT&E International，2005，38（6）：508-515.

［10］Janousek L.Variation of Eddy Current Density Distribution and its Effect on Crack Signal in Eddy Current Non-Destructive of Testing［J］.Advances in Electrical and Electronic Engineering，2011，5（1-2）：263-266.

［11］Yusa N，Janousek L，Miya K.Controlling Alternating Current Distribution Inside Conductive Material Leads to a Novel Volumetric Examination Method—Experimental Verification［J］.Materials transactions，2007，48（6）：1162-1165.

［12］Zhang Siquan，Nathan Ida，Wu Weihua.Thickness Measurement of Metal Coating Above Moving Conductive Plate by Rectangular Coil and Electromagnetic Method［C］//Proceedings of IEEE 12th International Conference on Electronic Measurement&Instruments（ICEMI）.Qindao：ICEMI.2015.1420-1425.

［13］Zhang Siquan，Tang Jiangfeng and Wu Weihua.Calculation Model for the Induced Voltage of Pick-up Coil Excited by Rectangular Coil Above Conductive Plate［C］//Proceedings of IEEE International Conference on Mechatronics and Automation（ICMA）.Beijing：ICMA，2015.1805-1810.

张思全（1971-），男，博士，副教授，研究方向为电磁场理论，无损检测与结构完整性评价技术，sqanz@126.com。

Theory Verification of Changing the Distribution of Eddy Current Inside Conductor by a New Phase Shifted Fields Probe*

ZHANG Siquan*，TANG Jiangfeng
（Department of Electrical and Automation，Shanghai Maritime University，Shanghai201306，China）

The Eddy Current Testing（ECT）method plays an important role in the nondestructive material test.Due to the skin effect，the conventional ECT method can only detect the surface defects of conductor.Some scholars have proposed a new phase shifted fields probe and drawn a conclusion from experiments that when the probe excited in certain conditions，the surface eddy current density of conductor can be suppressed and the deep eddy current density can be increased，so cracks located in deeper than standard depth of penetration can be detected.But the conclusion was only verified by experiment and without theory verification.The interaction between the phase shifted fields probe and the conductor is discussed using analytical method.The accurate theoretical expression of the eddy current distribution inside the conductor is derived and the influences of the phase and the exciting frequency are analysed.The results of the new probe can change the distribution of eddy current and increase the eddy current density in deep of conductor are verified using the analytical calculation method.

eddy current testing；skin depth；analytical calculation；phase shifted fields probe；eddy current distribution

TM154.1；TP391.7

A

1004-1699（2016）08-1169-07

EEACC：5140；7230；7310J10.3969/j.issn.1004-1699.2016.08.008

项目来源：国家自然科学基金项目（51175321）；上海海事大学校科研基金项目（20130463）

2015-10-23修改日期：2016-03-20