基于NA-MEMD和互信息的脑电特征提取方法*

韩　笑，佘青山，高云园，罗志增

（杭州电子科技大学智能控制与机器人研究所，杭州310018）

基于NA-MEMD和互信息的脑电特征提取方法*

韩笑，佘青山*，高云园，罗志增

（杭州电子科技大学智能控制与机器人研究所，杭州310018）

多变量经验模式分解（MEMD）方法不需要根据先验知识选取基函数，能同时对多通道数据进行自适应分解，适合于分析具有高度相关性和非平稳性的脑电信号。为了判别包含有用信息的内蕴模式函数（IMFs），提出一种基于噪声辅助多变量经验模式分解（NA-MEMD）和互信息的方法，并用于脑电特征提取。首先使用NA-MEMD算法对多通道信号进行分解得到多尺度IMF分量，然后采用互信息法分别计算各尺度上信号与其IMF分量、噪声与其IMF分量、信号IMF分量与噪声IMF分量之间的相关性，接着根据敏感因子筛选包含有用信息的IMF分量，将其叠加得到对应的重构信号，最后采用共同空间模式（CSP）法对重构信号进行特征提取，再用支持向量机（SVM）实现分类。使用仿真数据和实际数据集BCI Competition IV Data Set 1进行测试，与现有的其他方法比较，验证了所提方法的有效性。

脑电信号；噪声辅助多变量经验模式分解；互信息；共同空间模式

脑电信号EEG（Electroencephalogram）是大脑内部的神经细胞活动在大脑皮层的综合反映，包含着与大脑状况、思维过程等方面的相关信息。由于非植入式EEG相对简单快速，对人无损，同时具有较高的时间分辨率，因而成为BCI最重要的信号获取手段之一。但是，EEG通过头皮电极获取，信号非常微弱且背景噪声强［1］，因而从非线性、非平稳的EEG信号中准确快速地提取特定任务相关的有用信息具有重要意义。

国内外研究者提出了很多脑电特征提取的方法，主要包括自回归模型［2］、功率谱［3］、小波（包）变换［4-5］、共同空间模式 CSP（Common Spatial Pattern）［6-8］、熵［9］等。1998年，Huang等人［10］提出了一种完全由数据驱动的自适应的时频分析方法—经验模式分解EMD（Empirical Mode Decomposition），在生物电信号处理领域［11-13］得到了广泛研究，但会产生模式混叠现象［14］。为了解决该问题，Wu和Huang［14］提出了一种噪声辅助的改进算法EEMD（Ensemble）。它利用白噪声具有频率均匀分布的统计特性，当信号加入白噪声后，改变了信号极值点的特性，使信号在不同尺度上具有连续性从而有效的避免模式混叠。但是，EEMD和EMD都只能处理一维信号，不适合分析多通道数据［15］。2010年，Rehman等人［16］改进了经典的EMD算法，提出了多变量经验模式分解MEMD（Multivariate EMD）算法，可同时对多通道数据进行分解，能够避免各变量分解出的内蕴模式函数IMFs（Intrinsic Mode Functions）个数、频率不匹配问题，但仍然存在模式混叠问题。最近，Rehman等人［17］结合EEMD和MEMD的优点，又提出了噪声辅助的多变量经验模式分解NA-MEMD（Noise-Assisted）方法，能很好地解决这些问题。

尽管EMD及其扩展方法得到了广泛研究和应用，如何判定包含有用信息的IMFs是影响EMD方法应用效果的关键因素之一。目前研究大多数利用先验知识，如文献［18-20］根据研究对象已知的频率成分对IMFs进行选取。罗志增等［18］根据IMFs的瞬时频率衡量对应阶分量的有效度，选取有效度最高的分量建立AR模型用于手部运动识别。Park等［19］先用MEMD方法对信号和独立高斯白噪声通道分解出若干层（尺度）IMFs，计算各尺度IMFs的平均功率谱，然后根据运动想象脑电信号相关频率的先验信息选取有用的IMF分量，取得了优于EMD、连续小波变换和短时傅里叶变换的结果。Change等［20］根据与beta节律相关的神经元振荡活动规律，通过研究beta频带的IMFs的平均频率来选择重要的IMF分量。最近，Hu等［21］提出了一个不依赖先验知识的基于统计的IMFs识别方法，使用Wasserstein距离度量各尺度上信号IMF分量与噪声IMF分量之间的相似性来选取有用信息，在仿真数据和视觉皮层的局部场电位（LFP）神经数据中取得了较好的实验结果。

针对有效选择包含有用信息的IMF分量问题，本文提出了一种基于NA-MEMD和互信息的重要IMF分量识别方法，并结合CSP算法用于脑电特征的提取。首先，使用NA-MEMD同时对多通道的EEG和额外引入的噪声共同组成的信号进行分解，得到数量和频率一致的IMF分量。然后，利用互信息分别计算出各尺度信号及其IMF分量、噪声及其IMF分量、信号IMF分量与噪声IMF分量的相关性。接着，根据相关性得到的敏感因子筛选出有用的IMF分量并重构，使用CSP对重构信号进行特征提取，再用SVM算法对所提特征进行分类。最后，分别采用仿真数据和2008年BCI竞赛数据对所提方法进行测试，并于其他同类方法进行比较分析，实验结果验证了该方法的有效性。

1　基于NA-MEMD和互信息的特征提取方法

1.1噪声辅助的多变量经验模式分解

EMD方法的目的是将任意非线性、非平稳信号分解为若干个不同尺度的IMF和一个剩余分量。EMD分解后得到的每个IMF满足两个特征［10］：①整个IMF中零点数和极点数相等或至多相差1；②信号关于时间轴对称，即信号由局部极大值确定的包络线和由局部极小值确定的包络线均值为零。由于EMD算法的核心是筛选过程，不可避免地会出现模式混叠现象，即一个IMF包含了多个不同的信号分量，或同一信号分量出现在多个不同尺度的IMF中。此外，EMD都只能处理一维信号，不适合分析多通道数据。然而，在许多科学、工程领域，比如脑电信号处理中，信号经常以多通道时间序列形式被记录。

NA-MEMD方法是EMD的多变量扩展形式，可以自适应地对多个通道数据进行分解，同时展现不同通道信号的相位、幅值和频率信息。NA-MEMD不但充分利用了MEMD处理白噪声时具有的二元滤波器组特性，而且加入额外的独立的白噪声保证了MEMD分解后信号IMF分量与噪声IMF分量的可分离性。对于一个v变量的输入信号x（t）=｛x1（t），x2（t），…，xv（t）｝，NA-MEMD算法［17］的具体步骤如下：

①生成s通道的不相关高斯白噪声信号n（t）=｛n1（t），n2（t），…，ns（t）｝，其长度与原始信号x（t）等长，都为L；

②将步骤①中生成的s通道噪声信号n（t）加入到v通道信号x（t）中，构成q=s+v通道的多元信号z（t）=｛z1（t），z2（t），…zq（t）｝；

③在一个球面上，选择合适的q-1个采样点集，即得到q维空间的方向向量dθk；

④计算信号z（t）沿着方向向量dθk的投影，记作；

⑧计算细节信息ci（t）=z（t）-m（t），如果ci（t）满足多变量IMF的停止条件，则ci（t）被认为是第i阶IMF分量，计算残差ri（t）=z（t）-ci（t），对ri（t）重复上述步骤④～步骤⑧进行w次，当rw（t）变成一个单调函数，则停止筛分，否则对ci（t）重复上述步骤。

在本文中，NA-MEMD的最大分解层数是根据迭代筛选算法联合确定的。标准的EMD停止条件是在Ns个连续迭代步骤中零点数和极点数至多相差1时，筛选过程结束。通过引入包络幅值a（t），如式（1）所示，然后定义一个基于包络幅值的评价函数 f（t），如式（2）所示。当 f（t）小于或等于某个预设的阈值σ，结束筛选过程。根据文献［17］的推荐值，本文给定Ns=5和σ=0.075。

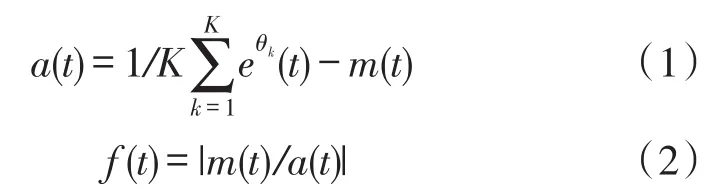
1.2互信息

在信息论中，互信息是信息熵的引申，常用来度量两个随机变量的相关性［22］。定义两个时间序列的熵为H（X）和H（Y），以及它们之间的联合熵为H（X，Y），分别计算如下：

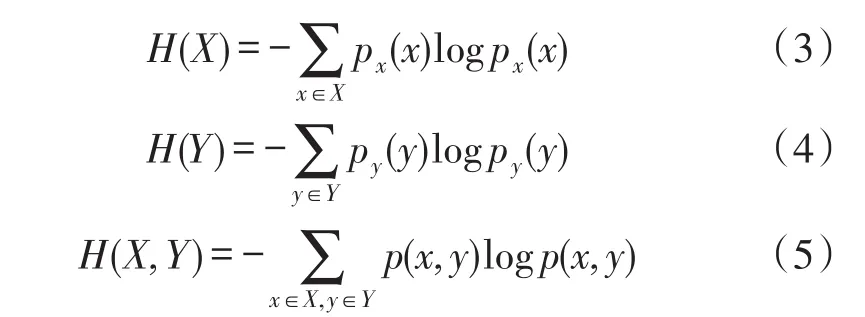
其中，p（x，y）是X和Y的联合概率密度，px（x）、py（y）分别是X、Y的边缘概率密度。于是，X和Y的互信息定义为：

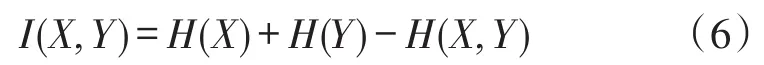
当X和Y是独立的，则I（X，Y）=0。

将互信息应用于脑电分析时，X和Y代表任意两个N导联、长度为L的脑电信号，用来测量多通道脑电信号的线性或非线性关系。本文用互信息来分析NA-MEMD分解出的多尺度IMF分量之间的相互关系，以筛选出包含有用信息的IMF分量。

1.3重要的IMF分量选择

当NA-MEMD分解出一系列IMF分量之后，如何鉴别包含有用信息的IMF分量仍是当前EMD研究的难点问题之一。

给定v通道信号x（t），随机生成s通道高斯白噪声信号n（t），共同组成q=s+v通道的多元信号z（t），z（t）= ｛x1（t），x2（t），…，xv（t），n1（t），n2（t），…，ns（t）｝。采用 MEMD 对z（t）进行分解，得到对应的q组IMF分量。基于NA-MEMD和互信息，本文提出了一种选择有用IMF分量的方法，具体步骤如下：

①计算原始信号x（t）的第i阶IMF分量cxi（t）与x（t）自身之间的互信息Ai。

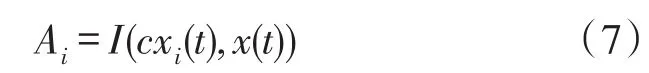
其中，cxi（t）=｛cx1i（t），cx2i（t），…，cxvi（t）｝，i=1，2，…，w，其中w表示最大分解层数。

②计算噪声信号n（t）的第i阶IMF分量cni（t）与n（t）自身之间的互信息Bi。

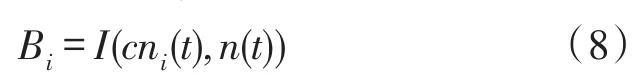
其中，cni（t）=｛cn1i（t），cn2i（t），…，cnsi（t）｝，i=1，2，…，w。

③计算原始信号x（t）的第i阶IMF分量cxi（t）与噪声信号n（t）的第i阶IMF分量cni（t）之间的互信息Ei。

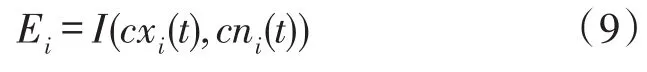
④分别计算第i阶IMF分量的敏感因子Ri：

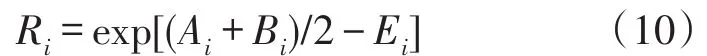
式中，敏感因子Ri的数值越大，则说明信号和噪声的第i阶分量与其自身之间的互信息Ai和Bi越大，信号的IMF分量与噪声的IMF分量之间的相关性Ei越小。简言之，第i阶的敏感因子Ri越大，表明第i阶的IMF分量包含的有用信息越多。

1.4特征提取

CSP方法是一种广泛用于脑电信号处理的特征提取方法［23］。该方法对协方差矩阵同时联合对角化，寻找一组空间滤波器，使经过它滤波投影后的信号中一类信号的方差最大，另一类信号的方差最小，从而最大化类间样本的距离。

本文提出的特征提取方法具体描述如下：首先采用NA-MEMD算法分解多通道脑电信号，得到各个尺度上的IMF分量，其次根据Ri的大小选取包含有用信息的IMF分量，然后叠加每个通道所选的重要分量得到各自对应的重构信号，最后采用CSP算法对重构信号进行特征提取。整个特征提取方法的流程图如图1所示。

2　实验结果与分析

2.1仿真数据实验

首先，使用一组仿真数据来验证本文方法。仿真信号是由正弦信号和随机高斯白噪声合成，三通道合成信号如下：

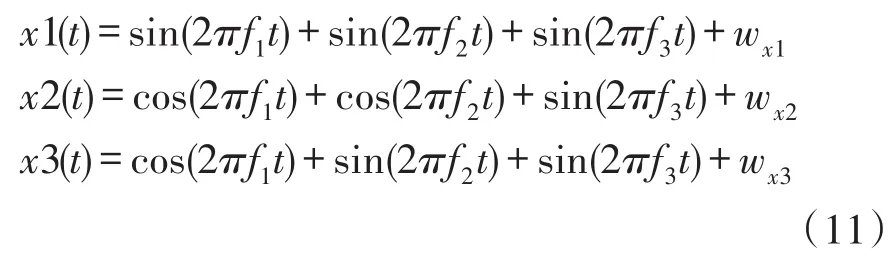
其中，t=1，2，…，1 000，f1=50/fs，f2=26/fs，f3= 12/fs，采样频率 fs为1 000 Hz。wx1，wx2和wx3分别为每个通道信号对应的随机高斯白噪声信号，信噪比为30 dB。在原始输入信号基础上，额外增加两个通道的与信号长度相同、方差为信号方差6%［23］的噪声信号n1和n2。

使用NA-MEMD对五通道的合成信号进行分解，结果如图2所示（由于空间有限，图中只显示前四个通道）。其中第一行为四个通道的原始信号，IMF1～IMF6是各通道数据分解得到的前6阶IMF分量，IMFr是分解余量。从图中可以看出，不同阶次的IMF分量包含不同的时间特征尺度，且随着阶次的增长，频率依次减小。对三个合成信号而言，IMF1～IMF3分量包含明显的毛刺且有混叠的现象，而IMF4～IMF6分量的波形比较整齐且有周期性，分别对应于原始信号中的三种频率成分。

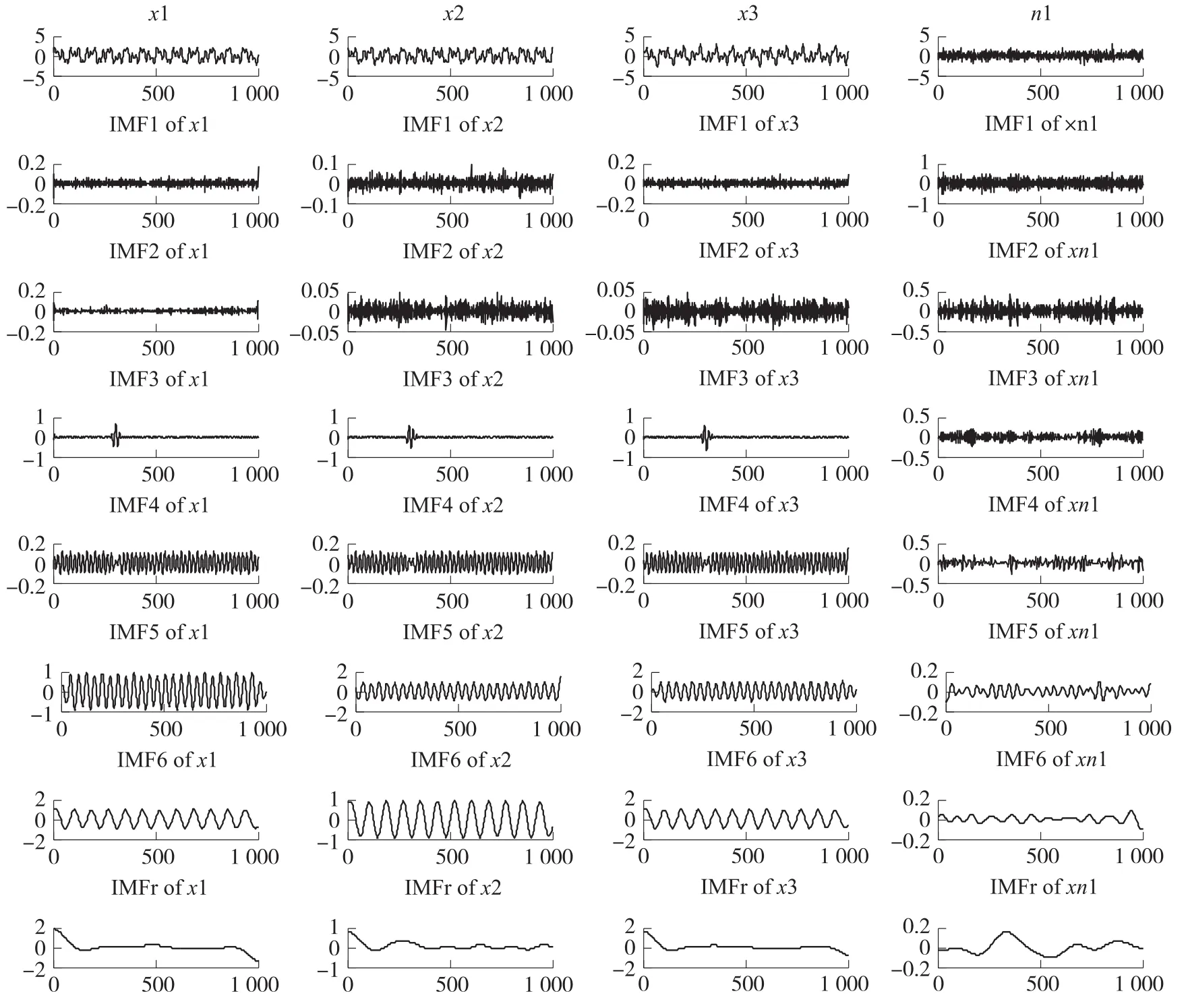
图2　对多通道仿真信号进行NA-MEMD分解的结果

利用互信息计算出各个阶次上IMF分量的敏感因子，表1给出了一次实验的结果。由表1可知，将前6阶的敏感因子由大到小排序，前3个分量分别为IMF4、IMF6和IMF5，所以应该选取包含有用信息的分量为第4、5、6阶，这与直接观察图2所示的分解结果是一致的。

表1　前6阶IMF分量的敏感因子

为了进一步验证所提方法的有效性，分别计算三通道各阶IMF分量的功率谱，如图3所示，其中IMF1～IMF6分别表示前6阶的IMF分量，IMFr表示剩余分量之和。图3（a）对应信号x1的功率谱，从图中可以看出，IMF6对应频率12 Hz，IMF5对应频率26 Hz，IMF4对应频率50 Hz，这与合成信号的频率成分一致。图3（b）和图3（c）分别对应信号x2和x3的功率谱，也可分析得出类似的结果。

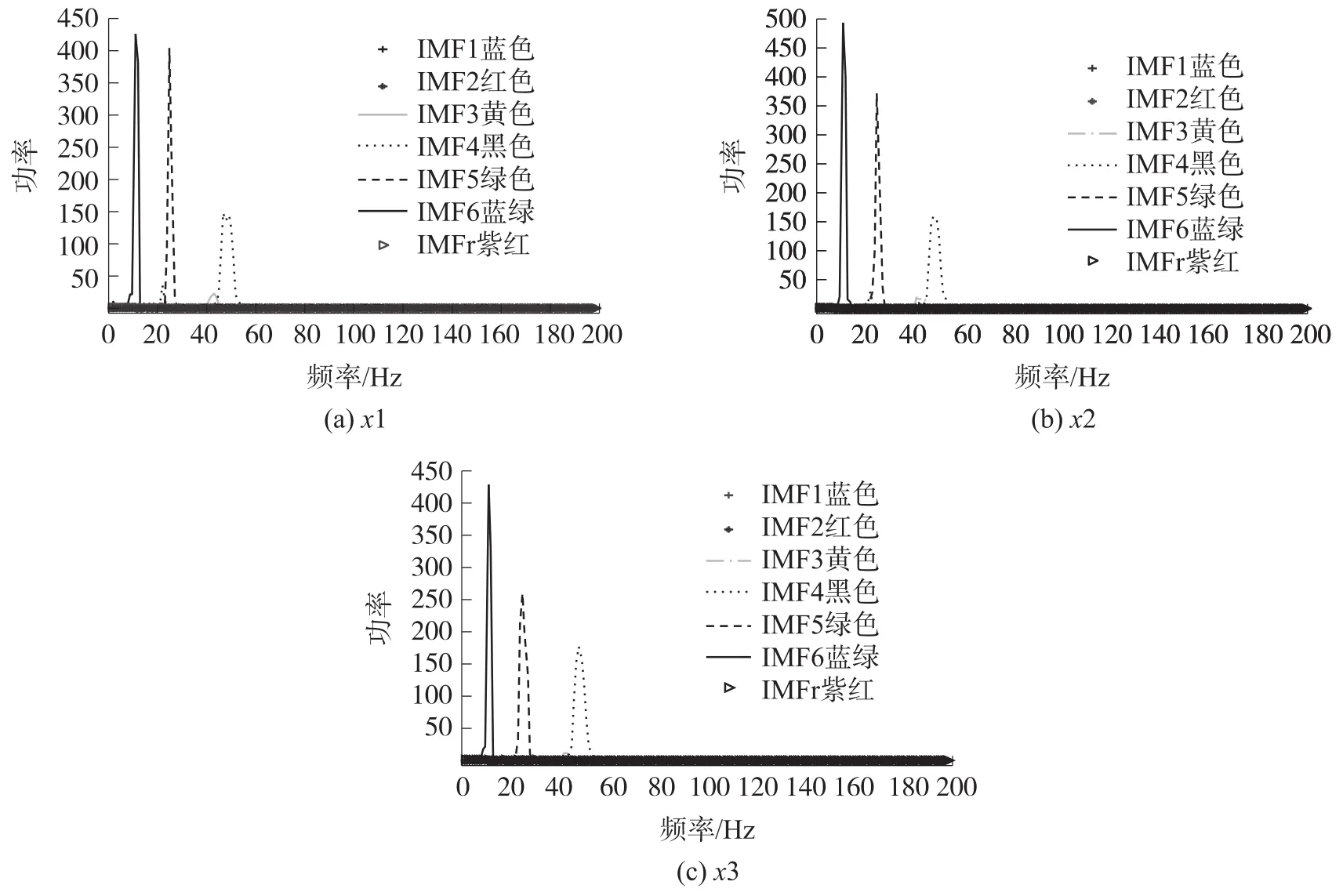
图3　三通道合成信号各阶IMF分量的功率谱

2.2脑电数据实验

2.2.1脑电数据

实验数据来自德国柏林研究中心2008年提供的BCI Competition IV Data Set 1运动想象脑电数据集［24］。该数据集记录了7名健康受试者按照实验要求执行运动想象任务的脑电信号数据，一共获得14组数据，其中包括7组标定数据和7组测试数据。本文选用受试者a、b、f、g提供的4组标定数据，每组数据包含59个通道的EEG信号，采样频率为100 Hz。每个受试者按照电脑屏幕的提示执行左手、右手、单或双脚三种运动想象任务中的两类。具体而言，受试者a和f执行左手和脚实验，受试者b和g执行左手和右手实验。每个受试者执行200次实验，每类任务执行100次。单次实验持续8秒：包括两秒电脑显示十字符号受试者安静准备时间，4秒受试者按照指令执行想象任务时间，以及两秒电脑黑屏显示的结束实验时间。

2.2.2数据处理

①预处理

为了方便对比，参照文献［19］的推荐，本文选取11个通道的脑电信号进行分析，分别对应10-20系统的“FC3”，“FC4”，“Cz”，“C3”，“C4”，“C5”，“C6”，“T7”，“T8”，“CCP3”，“CCP4”，然后使用8-30 Hz的5阶巴特沃兹滤波器对脑电数据进行滤波。采样频率为100 Hz，实际运动想象时间为4 s。

②特征提取

随机生成2个通道的信噪比为20 dB、长度与脑电信号长度一致的高斯白噪声时间序列［19］，作为独立的噪声通道加到11通道脑电信号中得到混合信号。使用NA-MEMD对该混合信号进行分解，得到维数为［通道数×IMF阶次×数据长度］的分解结果。为了方便显示，本文只画出受试者a在某单次实验中Cz、C3和C4共3个通道的分解图，如图4所示。其中，包括原始波形、分解得到的前6阶分量、以及剩余的其他分量之和。从图4可以看出，第1～6阶IMF分量的频率依次降低，这是符合NA-MEMD算法的分解规律的。另外，IMF1分量存在较多的毛刺，有可能包含一些噪声成分。

使用互信息计算出各阶IMF分量对应的敏感因子值。分别采用盒形图（box plot）统计分析四个受试者200次实验得到的各阶敏感因子的分布情况。由于NA-MEMD算法是数据驱动的自适应分解方法，即使同一受试者每个单次实验数据分解得到的阶数也是变化的，因此这里统一给出了前7阶的敏感因子分布，如图5所示。盒形图的两端分别表示各阶敏感因子的上、下四分位数，中线表示中位数，“+”表示温和异常点。

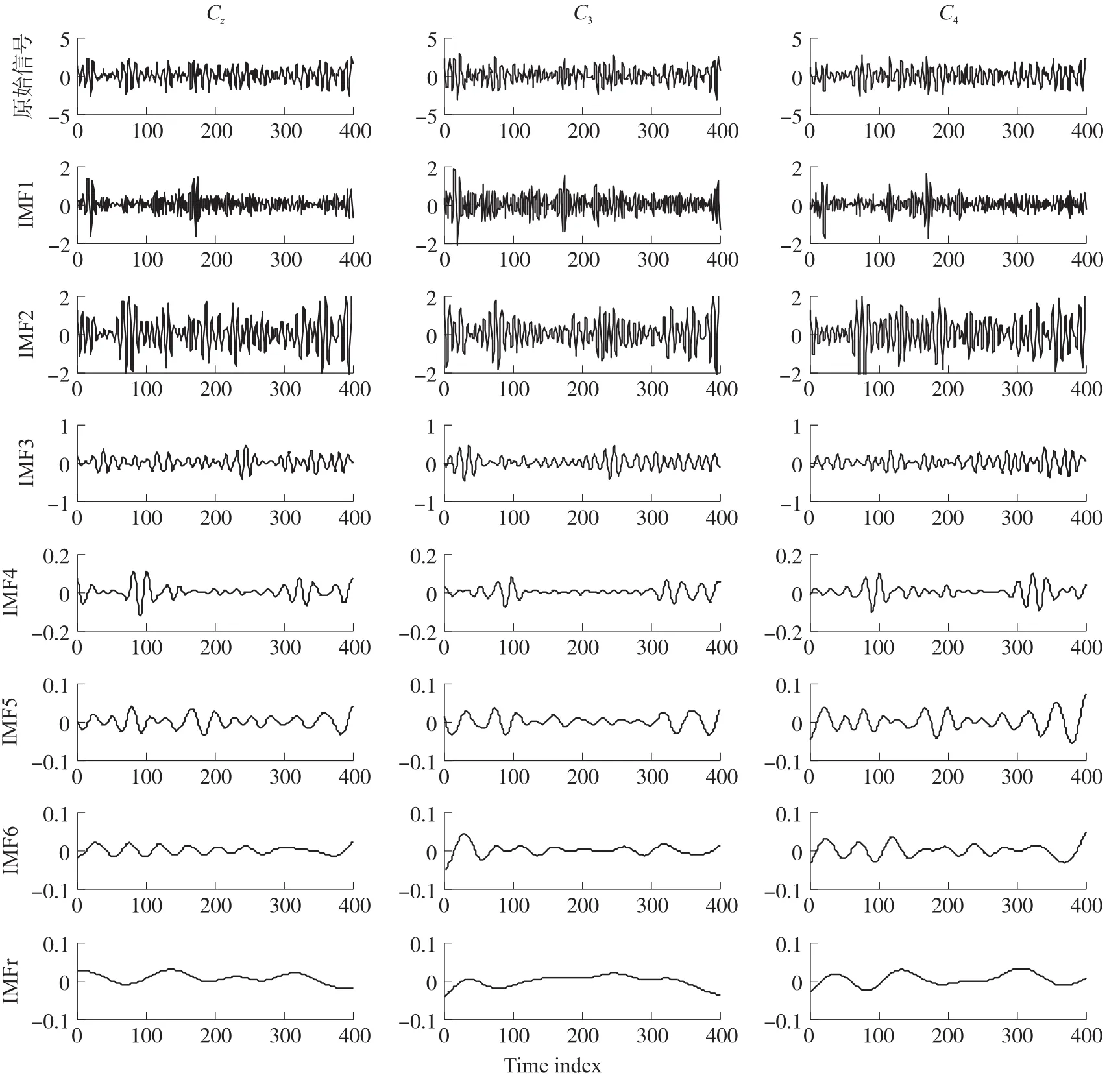
图4　三通道脑电信号的NA-MEMD分解

从图5可以看出，四名受试者的敏感因子分布情况各不相同，但是总体来说，都存在前三阶IMF分量对应的敏感因子较大，而其他阶较小的分布规律，尤其是3个受试者a、f和g的IMF2分量对应的敏感因子有显著的优势。根据敏感因子分布图，结合敏感因子值越大、包含有用信息越多的原则，可知IMF1～IMF3分量包含了较多的有用信息，这和文献［19］根据先验知识选取IMF2和IMF3为重要成分的结论是一致的。

目前，选取有用IMF分量的个数还没有统一的判断标准，本文依据最佳分类准确率最终选择个数为3。接下来，将所选取的包含有用信息的IMF分量进行重构。需要说明的是，虽然IMF1分量的敏感因子较大，但是如上面分解图4所示，该阶包含明显的毛刺。在进行重构时，如果直接丢弃该分量则可能会丢失有用信息，但若保留则会引入噪声干扰。所以，在重构过程中，使用两种策略：（1）直接选取敏感因子最大的前三阶分量重构；（2）加入判断条件，如果敏感因子最大的前三阶分量中包含了IMF1分量，则舍弃，只选取其他两阶分量用于重构。

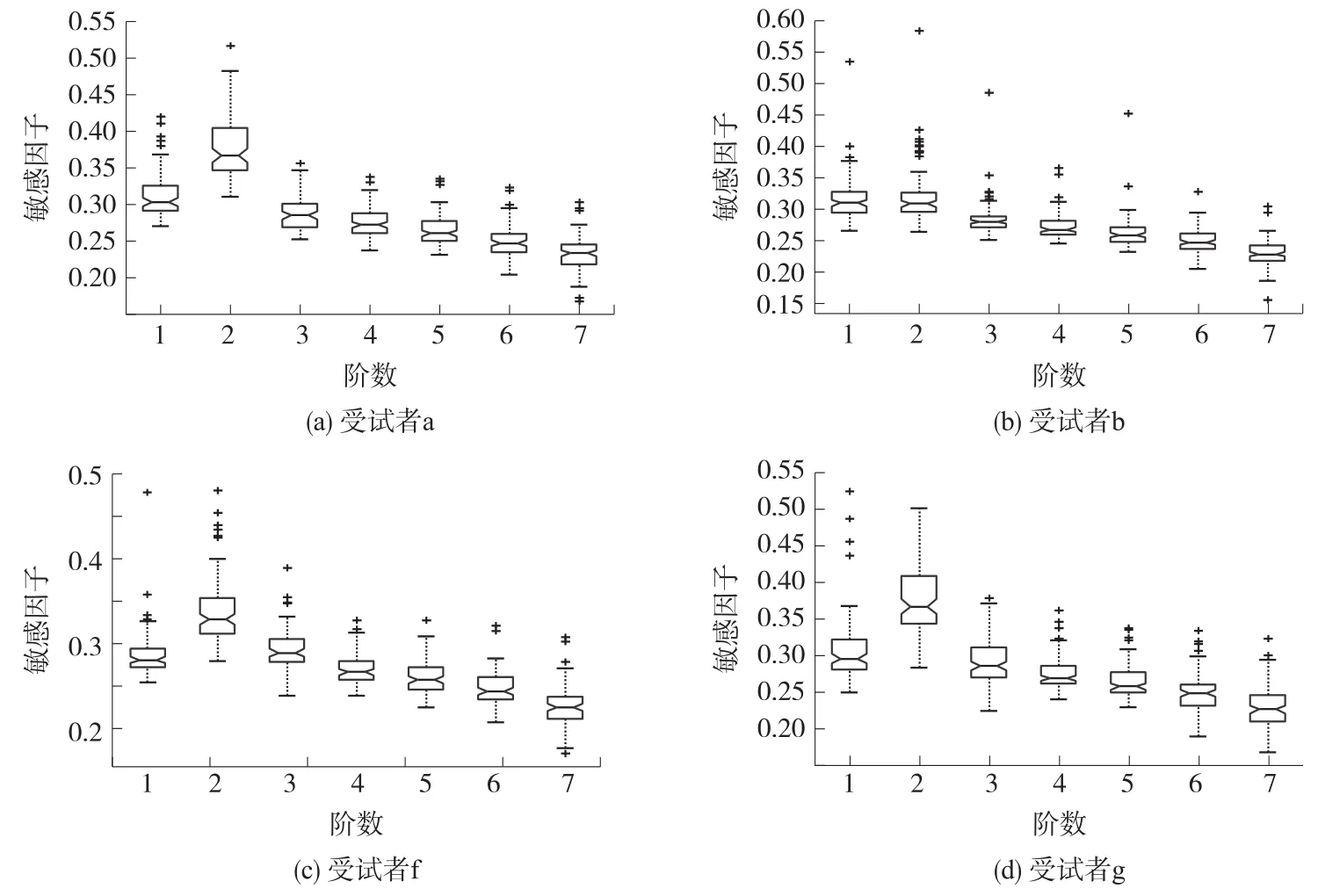
图5　四名受试者的敏感因子分布图

为了方便进一步与文献［19］对比，使用CSP方法对重构信号进行特征提取时，特征向量的维数取4，一共得到［200×4］维的特征向量。分别做出受试者a想象执行两类各100次的特征向量。第一和第四个特征值曲线如图6所示。在图6中，红色曲线和绿色曲线分别表示受试者a执行第一类（左手）和第二类（脚）想象任务时的特征值。从图中可以观察到，第一类的第一个特征值比第二类的小，而第四个特征值正好表现出相反的特性，特征值的总体区分度都比较好。

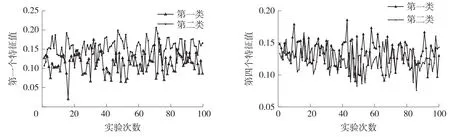
图6　受试者a特征提取后得到的2个特征值

③分类

为了进一步验证所提方法的有效性，将提取出的特征向量送入到分类器中进行分类。支持向量机SVM（support vector machine）能较好地解决高维数、小样本和非线性等实际问题，近年来广泛应用于肌电、脑电、心电等生理信号的分类［25］，因此本文使用SVM对脑电特征进行分类。

在使用SVM分类前，训练样本和测试样本按140∶60的固定比例随机选择数据，并将训练数据和测试数据都归一化到［0，1］区间。SVM的核函数选择分类效果较稳定的高斯核函数。在训练时使用5折交叉验证，并使用网格搜索法寻找最佳惩罚系数C和高斯核宽度gamma。通过训练建立SVM分类模型，并使用该模型对测试集进行预测。重复上次分类过程100次，得出平均分类准确度，对结果进行统计和分析。

2.2.3结果分析

按照之前的两种重构策略，将本文提出的基于互信息的IMFs选择方法分别记作NA-MEMD-MI1 和NA-MEMD-MI2，重构信号时前者不忽略IMF1值，后者忽略。将本文方法分别与文献［19］提出的基于平均功率谱的IMFs选择方法（NA-MEMD-PS）、文献［21］设计的基于 Wasserstein距离测度的IMFs选择方法（NA-MEMD-WD）进行对比。所有方法的数据来源一致，预处理方法一样，在CSP特征提取和SVM分类方法中使用相同的参数设置，分类性能（平均准确率和标准差）的对比结果如表2所示。

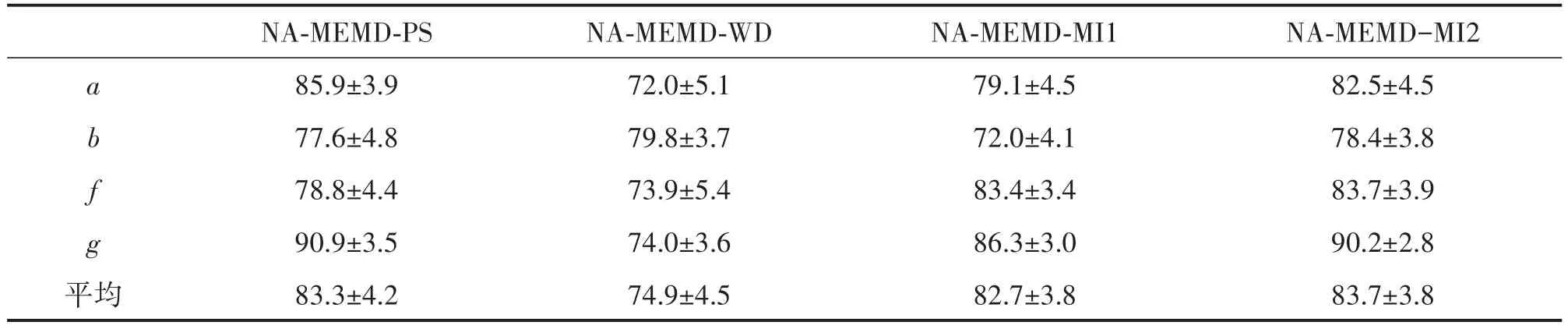
表2　几种方法的分类性能比较（均值±标准差（%））

从表2可以看出，对于受试者a，本文方法NA-MEMD-MI1和NA-MEMD-MI2的分类效果要好于NA-MEMD-WD，但低于NA-MEMD-PS；对于受试者b，NA-MEMD-WD的准确率相对最高，NA-MEMD-MI2略高于NA-MEMD-PS；对于受试者f，NA-MEMD-MI1和NA-MEMD-MI2的结果好于其他两种方法；对于受试者 g，NA-MEMD-MI1、NA-MEMD-MI2和NA-MEMD-PS均取得了较高的识别率。这说明不同受试者的个体差异对分类结果有一定的影响。相较于其他方法，本文方法取得了较好的平均分类准确率，NA-MEMD-MI1为82.7%，NA-MEMD-MI2达到83.7%。从整体来看，本文方法能够比较正确地区分两类运动想象任务，体现了其在EEG特征提取与分类上的有效性。

3　结论

本文基于NA-MEMD与互信息提出了一种有效的有用信息成分鉴别方法，应用于脑电信号的特征提取。首先使用NA-MEMD算法对多通道脑电信号进行分解得到多尺度IMF分量，然后采用互信息法分别计算各尺度的敏感因子并识别出包含有用信息的IMF分量，叠加得到各通道对应的重构信号，最后采用共同空间模式（CSP）算法提取出重构信号的特征向量，通过支持向量机（SVM）完成特征向量的分类。采用2008年BCI Competition IV Data Set 1数据进行实验验证，并与其他方法进行了比较，结果表明本文方法可以有效地区分多名受试者执行的不同运动想象任务，获得了较好的分类性能。因此，本文方法能有效判别与特定任务相关的重要信息成分，为脑电信号的特征提取提供了新的思路。

［1］吴明权，李海峰，马琳.单通道脑电信号中眼电干扰的自动分离方法［J］.电子与信息学报，2015，37（2）：367-372.

［2］Burke D P，Kelly S P，Chazal P，et a1.A Parametric Feature Extraction and Classification Strategy for Brain-Computer Interfacing ［J］.IEEE Transactions on Neural System and Rehabilitation Engineering，2005，13（1）：12-17.

［3］Hu S Q，Tian Q Q，Cao Y，et al.Motor Imagery Classification Based on Joint Regression Model and Spectral Power［J］.Neural Computation and Applications，2013，23（7-8）：1931-1936.

［4］颜世玉，刘冲，赵海滨，等.基于小波包分解的意识脑电特征提取［J］.仪器仪表学报，2013，33（8）：1748-1752.

［5］罗志增，周镇定，周瑛，等.双数复小波特征在运动想象脑电识别中的应用［J］.传感技术学报，2014，27（5）：575-580.

［6］Rozado D，Duenser A，Howell B.Improving the Performance of an EEG-Based Motor Imagery Brain Computer Interface Using Task Evoked Changes in Pupil Diameter［J］.PLOS ONE，2015，10 （3）：e0121262.

［7］Li Y，Koike Y.A Real-Time BCI with a Small Number of Channels Based on CSP［J］.Neural Computing and Applications，2011，20（8）：1187-1192.

［8］佘青山，昌凤玲，范影乐，等.基于邻接矩阵分解的脑电特征提取与分类方法［J］.传感技术学报，2012，25（9）：1204-1209.

［9］Jiang G J A，Fan S Z，Abbod M F，et al.Sample Entropy Analysis of EEG Signals Via Artificial Neural Networks to Model Patients’Consciousness Level Based on Anesthesiologists Experience［J］. BioMed Research International，2015，2015（343478）：1-8.

［10］Huang N E，Zheng S，Steven R，et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear Non-Stationary Time Series Analysis［C］//Proceedings of the Royal Society of London A：Mathematical，Physical and Engineering Sciences.London，The Royal Society Press，1998，454（1971）：903-995.

［11］Kouchaki S，Sanei S，Arbon E L，et al.Tensor Based Singular Spectrum Analysis for Automatic Scoring of Sleep EEG［J］.IEEE Transactions on Neural Systems and Rehabilitation Engineering，2015，23（1）：1-9.

［12］谢平，陈晓玲，苏玉萍，等.基于EMD-多尺度熵和ELM的运动想象脑电特征提取和模式识别［J］.中国生物医学工程学报，2013，32（6）：641-648.

［13］李明爱，崔燕，杨金福，等.基于HHT和CSSD的多域融合自适应脑电特征提取方法［J］.电子学报，2013，41（12）：2479-2486.

［14］Wu Z，Huang N E.Ensemble Empirical Mode Decomposition：A Noise-Assisted Data Analysis Method［J］.Advances in Adaptive Data Analysis，2009，1（1）：1-41.

［15］Park C，Plank M，Snider J，et al.EEG Gamma Band Oscillations Differentiate the Planning of Spatially Directed Movements of the Arm Versus Eye：Multivariate Empirical Mode Decomposition Analysis［J］.IEEE Transactions on Neural Systems and Rehabilitation Engineering，2014，22（5）：1083-1096.

［16］Rehman N，Mandic D P.Multivariate Empirical Mode Decomposi-tion［C］//Proceedings of the Royal Society A：Physical and Engineering Sciences，London，The Royal Society，2010，466（2117）：1291-1302.

［17］Rehman N，Mandic D P.Filter Bank Property of Multivariate Empirical Mode Decomposition［J］.IEEE Transactions on Signal Processing，2011，59（5）：2421-2426.

［18］罗志增，马文杰，孟明，等.一种基于HHT和AR模型的手部运动模式识别方法［J］.模式识别与人工智能，2008，21（2）：227-232.

［19］Park C，Looney D，Ahrabian A，et al.Classification of Motor Imagery BCI Using Multivariate Empirical Mode Decomposition［J］. IEEE Transactions on Neural Systems and Rehabilitation Engineering，2013，21（1）：10-22.

［20］Chang H C，Lee P L，Lo M T，et al.Inter-trial Nalysis of Post-Movement Beta Activities in EEG Signals Using Multivariate Empirical Mode Decomposition［J］.IEEE Transactions on Neural Systems and Rehabilitation Engineering，2013，21（4）：607-615.

［21］Hu M，Liang H.Search for Information-Bearing Components in Neural Data［J］.PLOS ONE，2014，9（6）：e99793.

［22］Melia U，Guaita M，Vallverdu M，et al.Mutual Information Measures Applied to EEG Signals for Sleepiness Characterization［J］. Medical Engineering&Physics，2015，37（3）：297-308.

［23］Samek W，Kawanabe M，Muller K-R.Divergence-Based Framework for Common Spatial Patterns Algorithms［J］.IEEE Transactions on Biomedical Engineering，2014，7：50-72.

［24］Blankertz B，Dornhege G，Krauledat M，et al.The Non-Invasive Berlin Brain-Computer Interface：Fast Acquisition of Effective Performance in Untrained Subjects［J］.NeuroImage，2007，37 （2）：539-550.

［25］高发荣，王佳佳，席旭刚，等.基于粒子群优化-支持向量机方法的下肢肌电信号步态识别［J］.电子与信息学报，2015，37 （5）：1154-1159.

韩笑（1991-），女，河南南阳人，硕士，从事脑电信号处理与脑-机接口应用方面的研究，754163862@qq.com；

佘青山（1980-），男，湖北荆州人，博士，杭州电子科技大学自动化学院，副教授，硕士生导师，从事生物信息处理与分析、机器学习、模式识别、智能控制等领域的研究，qsshe@hdu.edu.cn。

Feature Extraction of EEG Based on NA-MEMD and Mutual Information*

HAN Xiao，SHE Qingshan*，GAO Yunyuan，LUO Zhizeng
（Institute of Intelligent Control and Robotics，Hangzhou Dianzi University，Hangzhou 310018，China）

Multivariate empirical mode decomposition is suitable to analyze electroencephalography（EEG）signals of non-stationary characteristics and high correlation between different channels，due to the fact that it can adaptively decompose multi-channel data and has no need to select basis function using prior knowledge.To identify the intrinsic mode functions（IMFs）containing available information，a novel identification method is proposed based on noise-assisted multivariate empirical mode decomposition（NA-MEMD）and mutual information，and then used for feature extraction of EEG signals.Firstly，multi-channel EEG signals are decomposed by the NA-MEMD algorithm to obtain the IMFs at each scale.Secondly，mutual information is used to calculate the correlation between crosschannel EEG signals and their IMFs，noise signals and their IMFs，EEG signals’and noise signals’IMFs，respectively，and then the information-bearing IMFs are recognized according to sensitive factors and used to obtain corresponding reconstructed signals by adding them together.Finally，the common spatial pattern（CSP）approach is employed to extract features of the reconstructed signals and support vector machine（SVM）is then applied for classification.The efficiency of the propose method has been demonstrated by comparisons with other existing algorithms on both synthetic data and real BCI Competition IV Data Set 1.

EEG signals；Noise-assisted multivariate empirical mode decomposition（NA-MEMD）；mutual information；common spatial pattern（CSP）

TP391

A

1004-1699（2016）08-1140-09

EEACC：7230J；7150D10.3969/j.issn.1004-1699.2016.08.003

项目来源：浙江省自然科学基金项目（LY15F010009）；国家自然科学基金项目（61201302，61172134，61201300）

2016-01-13修改日期：2016-03-31