基于高阶补偿器的加速度传感器动态误差补偿方法*
赵宁宁,王建林,魏青轩,于 涛,赵利强
(北京化工大学信息科学与技术学院,北京100029)
基于高阶补偿器的加速度传感器动态误差补偿方法*
赵宁宁,王建林*,魏青轩,于涛,赵利强
(北京化工大学信息科学与技术学院,北京100029)
加速度传感器动态特性对其动态测量结果具有重要影响。为了改善加速度传感器动态性能,减小动态误差,提出了一种基于高阶补偿器的加速度传感器动态误差补偿方法,该方法通过建立加速度传感器ARX模型,利用加速度传感器模型极点确定高阶补偿器的阶次,并应用误差白化算法(EWC)获得高阶补偿器的参数,实现加速度传感器的动态误差补偿。实验结果表明,该方法有效改善了加速度传感器的动态特性,且高阶补偿器的补偿效果优于低阶补偿器的补偿效果。高阶补偿器补偿后传感器输出超调量和残差均是低阶补偿后的三分之一,响应时间是低阶补偿后响应时间的一半左右。
加速度传感器;高阶动态补偿器;ARX模型;误差白化参数辨识
冲击加速度在产品抗冲击破坏能力试验中是十分重要的测量参数,如汽车安全碰撞、子弹侵彻钢板试验等[1-4]。冲击碰撞试验中产生的冲击加速度的频率可达10 kHz,要保证冲击加速度的测量精度,加速度传感器的工作频带要大于10 kHz。但现有加速度传感器的工作频带一般为5 kHz,如美国GST公司的加速度传感器工作频带为3 kHz,OMEGA公司的加速度传感器工作频带为5 kHz,均小于测量冲击加速度频率上限,使测量结果的动态测量误差较大,不能满足冲击加速度测量需求。为了减小加速度传感器动态测量误差,扩大加速度传感器的适用范围,迫切需要对加速度传感器进行动态误差补偿[5-7],拓宽加速度传感器工作频带。
对传感器进行动态误差补偿常采用串接动态补偿滤波器的方法,动态补偿滤波器分为动态补偿数字滤波器和动态补偿模拟滤波器两种。动态补偿数字滤波器具有可软件实现,无需增加任何硬件,具有灵活性等优点,因此得到广泛应用。张铁头等[8]利用模糊LS-SVM法对微硅加速度传感器进行动态补偿,减小了微硅加速度传感器动态测量误差,但模糊LS-SVM迭代次数多,计算复杂,对训练数据要求高;
潘保青等[9]利用量子粒子群优化算法建立热电偶传感器动态补偿滤波器,有效改善了热电偶传感器的动态特性,减小了传感器动态测量误差;Junqing Ma等[10]利用机器臂传感器一阶传递函数和补偿后期望的传递函数直接给出补偿滤波器传递函数,拓宽了机器臂传感器频带,改善了机器臂传感器的动态性能,但此方法对机器臂传感器模型精度要求较高;刘清等[11]利用理想参考模型和系统辨识方法得到微硅加速度传感器二阶动态补偿滤波器的参数,扩展了微硅加速度传感器频带,改善了其动态特性,但微硅加速度传感器模型为传统二阶模型。上述传感器动态补偿方法将传感器近似为二阶系统,然后针对二阶系统进行动态补偿,主要有零极点配置法和参数辨识法,结果表明传感器动态补偿效果较显著,但补偿效果受二阶模型参数精度影响较大。而有的传感器用辨识法建立的模型不是二阶系统,而是一个高阶系统,因此利用加速度传感器输入输出数据辨识其高阶模型阶次和参数,模型更精确[12];根据加速度传感器高阶模型及测试要求指标,设计相应的高阶动态补偿滤波器更具有实际意义,更符合工程应用。
本文针对加速度传感器动态性能改善问题,提出一种基于高阶补偿器的加速度传感器动态误差补偿方法,利用加速度传感器输入输出数据建立其ARX模型,利用加速度传感器模型极点确定高阶动态补偿滤波器的阶次,应用误差白化辨识算法获得高阶动态补偿滤波器参数,实现加速度传感器动态性能的改善,减小加速度传感器的动态测量误差。
1 加速度传感器动态补偿原理
一种基于参考模型[11]的动态补偿滤波器设计方法如图1所示。

图1 动态补偿原理图
其中u(k)为加速度传感器输入信号,y(k)为加速度传感器输出信号,yd(k)为参考模型输出信号,yc(k)为补偿器输出信号,θ是动态补偿器的待辨识参数。
一种较为理想的补偿方法是在加速度传感器之后串接一个零点等于加速度传感器传递函数极点的动态补偿环节W(z)且有:

式中:a0,a1,…,an为加速度传感器离散传递函数特征方程的系数,n为加速度传感器阶次。
此时补偿后的加速度传感器满足不失真响应条件。由奈奎斯特准则可知由式(1)构成的补偿环节是不稳定的,可以利用一个非理想补偿环节进行补偿,减小动态测量误差,使加速度传感器能够满足测试要求。设补偿后加速度传感器的传递函数为一个响应特性较好的二阶系统,即

ωn和ε分别为系统的固有频率和阻尼比。
典型二阶系统频率特性曲线如图2所示。

图2 典型二阶系统频响图
ωb为系统闭环截止频率,即对数幅频M(ω)由频率为零时分贝值下降3 dB时的频率;ωM为被测信号带宽,ωr为系统谐振频率;ωn为参考模型自然震荡频率,其中ωb与ωn的关系式[13]为

ε为阻尼比。保证加速度传感器测量结果的精确度,ωb与ωM的关系一般为

根据式(3)和式(4)可知ωn与ωM的关系为

故可以根据冲击加速度信号的频带来确定参考模型ωn。
参考模型阶跃响应超调量σp与阻尼比ε的关系为
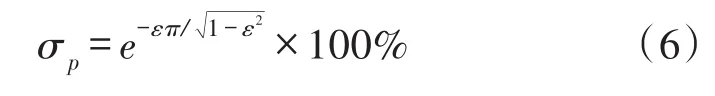
阻尼比ε越小,σp越大,当超过40%时,参考模型不符合加速度测量瞬态响应指标的要求,工程上[14-15]一般将ε设置在0.4~0.7之间,能保证加速度传感器动态特性较好。
利用式(5)和式(6)可确定参考模型未知参数ωn和ε。
2 高阶动态补偿滤波器的阶次及参数确定
2.1加速度传感器ARX模型建立
加速度传感器为单输入单输出线性定常系统,其ARX模型结构为

式中,u(k)为加速度传感器输入值;y(k)为加速度传感器输出值;e(k)为加速度传感器输出噪声。

d-1为后移位算子,n、m为加速度传感器模型阶次。
ARX模型属于一种“黑箱”模型,无需知道复杂的物理机理,直接利用系统输入输出数据,通过系统辨识方法确定其模型结构和参数[16]。模型结构简单,鲁棒性强,在噪声较小时辨识精度高,在噪声较大时,可以适当提高模型的阶次来抵消噪声对辨识精度的影响。
加速度传感器ARX模型建立步骤如下:
①对加速度实验数据进行去噪、去除趋势预处理
②由加速度输入输出序列{u(k)},{y(k)}构造输入数据向量

确定目标函数

设定未知参数向量

③确定加速度传感器模型阶次
利用AIC(赤池信息准则)估计加速度传感器ARX模型的阶次

式中,V是损失函数,d是待估计参数的个数,N是估计数据样本的数量,通过寻找一个具有较小AIC值的估计模型来决定模型的阶次n、m。
④辨识加速度传感器模型参数
在确定模型阶次的基础上,利用最小二乘(LS)算法辨识模型参数,LS算法通过使目标函数J(θ)最小化来获得模型参数。
⑤模型验证
加速度传感器模型输出数据与实际实验数据进行对比。
2.2高阶动态补偿器阶次确定
一个高阶系统可以分成若干子系统,整个高阶系统阶跃响应时间近似等于响应时间最长的子系统的响应时间。
设加速度传感器高阶系统阶跃相应时间为ts,子系统的响应时间为ti,i=1,2…则有

设补偿后加速度传感器阶跃响应时间为tt,若tt满足式子(13)

且tt<ti的实数极点组成的子系统个数为n1,tt<ti的复数极点组成的子系统个数为n2,则说明阶跃响应时间比tt大的子系统有n1+n2个,则需要对2n1+n2个加速度传感器极点进行改善,则补偿器的阶次为n

加速度传感器子系统阶跃响应时间ti计算步骤如下:
①加速度传感器ARX模型离散传递函数为

式中 n≥m,λi和 pi分别为G(z)的零点和极点。
加速度传感器单位阶跃响应为

式中系数

pr是实数极点,pl复数极点。

②当极点 p是实数极点时,子系统是一阶系统。一阶系统的响应时间近似为

③当极点 p为复数极点时,子系统是二阶系统,例如p1,2=α±jβ,二阶系统的响应时间近似为

根据补偿后加速度传感器阶跃响应时间tt及式(12)~式(19)可得到补偿器阶次n。
2.3高阶动态补偿器参数辨识
以均方误差为目标函数的辨识算法在输入输出数据存在较大噪声时不能得到参数的无偏估计。本文采用误差白化算法[11]来克服噪声的干扰,得到高阶补偿器参数的无偏估计值。
动态补偿器的离散传递函数可以表示为:

其中θT=[a1,a2,…,ap,b0,b1,…,bq]为补偿滤波器的待辨识参数;p,q为补偿滤波器W(z)的阶次。加速度传感器的输出端存在测量噪声e(k)时,补偿器输出可以表示为

设补偿滤波器输入噪声向量为


其中

则带噪声的补偿滤波器输出信号为

设补偿滤波器输出误差为ζ,


式中L为滞后时间,由于测量噪声ɛ(k)是白噪声,所以当L≥p+q+1时

2.4加速度传感器动态补偿实现
图3是加速度传感器高阶动态补偿器设计的流程图。

图3 加速度传感器高阶动态补偿器设计流程图
对实验数据进行预处理主要是消除数据趋势项和部分噪声,而不能把噪声完全消除。在加速度传感器实际补偿中,传感器输出端不可避免的存在噪声,这时可以采用误差白化辨识算法辨识补偿器参数。具体步骤如下:
Step 1由加速度传感器校准系统获得输入输出数据,并对数据进行预处理;
Step 2辨识系统最佳模型结构,并建立系统模型;
Step 3根据系统零极点确定最佳补偿器阶次;
Step 4应用误差白话算法辨识补偿器参数;
Step 5加速度传感器补偿前后特性对比。
3 实验与分析
3.1实验系统
本文采用中国计量科学研究院的加速度传感器绝对法冲击激励系统来获得加速度传感器实验数据。该系统构成部分主要有由高压仓、弹丸、波形调整垫、Hopkinson杆、被校加速度传感器、激光多普勒干涉仪、放大器、PC和PXI采集器,如图3所示。利用上述装置对选定的加速度传感器进行实验,采样频率为2 MHz。采集得到峰值为4 950 gn的冲击加速度信号及加速度传感器输出电压信号,建立加速度传感器ARX模型。

y(t)是加速度传感器的输出电压值,u(t)是加速度传感器输入加速度值,e(t)是加速度传感器输出噪声。
由于本文实验数据采样率较高,数据量较大,表1只列出了输入加速度信号峰值附近对应的18组数据。图4给出了加速度传感器实测输出曲线与模型预测输出曲线的对比图。

图4 基于Hopkinson杆的冲击校准系统及加速度频率相应曲线图

表1 加速度传感器实测输出电压值和动态模型预测输出值对比(am1=4 950 gn)

图5 加速度传感器输出对比曲线与频率特性曲线
加速度传感器闭环极点为:

根据式(19)计算传感器阶跃响应时间近似为200 μs。根据工程上确定工作频带的方法及加速度频响图得到加速度传感器幅值误差为±5%的工作频带为6.4 kHz。工作频带较窄,动态特性较差,不能满足冲击加速度测量要求,需要对加速度传感器进行动态补偿。根据测量要求,补偿后加速度传感器工作频带15 KH,阻尼比为0.6,根据式(5)和式(6)得

参考模型离散传递函数为

参考模型传递函数为

参考模型阶跃响应时间约为100 μs,根据式(15)~式(19)得高阶补偿器阶次为4阶。
3.2实验与分析
分别设计低阶(二阶)和高阶(四阶)动态补偿器,分析补偿效果。
低阶动态补偿器辨识参数为

低阶动态补偿滤波器离散传递函数为

仿真实验中,输入为峰值为1000 gn的阶跃,加速度传感器输出分别经过W1(z)和W2(z)补偿器处理,并对补偿器输出进行去噪处理后得到的仿真结果如图6所示。

图6 低阶补偿器与高阶补偿器补偿效果对比图
由图6可知,低阶补偿器补偿后加速度传感器阶跃响应时间约为t1=160μs,高阶补偿器补偿后加速度传感器阶跃响应时间约为t2=100μs。

计算补偿后加速度传感器输出与参考模型输出误差平方和

yd为参考模型输出,yc(k)为补偿后加速度

高阶补偿器补偿后加速度传感器输出误差为

高阶动态补偿器辨识参数为

高阶动态补偿器离散传递函数为

可知

低阶补偿器补偿后加速度传感器输出超调量σ1=0.241,高阶补偿器补偿后加速度传感器输出超调量σ2=0.082。

由式(27)、式(29)、式(30)可知高阶补偿器和低阶补偿器都加快了加速度传感器响应速度,改善了加速度传感器动态特性,但高阶补偿器补偿效果明显优于低阶补偿器补偿效果。
高阶动态补偿器补偿前后加速度传感器的频率特性的变化如图7所示。

图7 补偿前后系统频率特性对比图
根据图7计算补偿后加速度传感器幅值误差为±5%的工作频带为15.4 kHz,大于补偿前6.4 kHz。
4 结论
本文所提出的基于高阶补偿器的加速度传感器动态误差补偿方法,利用加速度传感器输入输出数据辨识其模型阶阶次和参数,更精确描述加速度传感器特性;结合加速度AXR模型和误差白化算法,确定补偿器阶次和参数,实现了比低阶补偿器更好的补偿效果。
[1]刘立军,租静,范锦彪,等.动能子弹侵彻钢板加速度测试与分析[J].传感器与微系统,2010,29(6):15-17.
[2]范锦彪,徐鹏,王燕,等.高速动能弹侵彻钢板加速度测试技术研究[J].弹箭与制导学报,2008,28(2):123-126.传感器输出。低阶补偿器补偿后加速度传感器输出误差为
[3]李文才,徐鹏.高g值冲击下援助壳缓冲数据仿真[J].机械设计与制造,2014,8(4):205-207.
[4]文丰,石云波,周振,等.基于MEMS的高g值加速度计及在炮弹寝车双层钢靶试验中的应用[J].震动与冲击,2013,32 (19):165-169.
[5]Sascha Eichstädt,Alfred Link,Thomas Bruns,et al.On-Line Dynamic Error Compensation of Accelerometers by Uncertainty-Optimal Filtering[J].Measurement,2010,43:708-713.
[6]刘刚,刘学仁.基于递归神经网络的加速度传感器动态特性补偿[J].传感器与微系统,2007,26(7):70-72.
[7]Schoen M P.Dynamic Compensation of Intelligent Sensors[J]. IEEE Trans Instrum Meas,2007,56(5):1992-2001.
[8]张铁头,李杰.模糊LS-SVM在加速度传感器动态补偿中的应用[J].中国测试,2012,38(5):66-69.
[9]潘保青,李岩峰,张志杰,等.基于量子粒子群算法的热电偶动态校准及动态补偿技术研究[J].传感技术学报,2015,28(7):992-996.
[10]Junqing Ma,Aiguo Song,Dongcheng Pan.Dynamic Compensation for Two-Axis Robot Wrist Force Sensors[J].Journal of Sensors,2013,7(26):110-115.
[11]刘清,曹国华.模型参考和误差白化的传感器动态补偿算法[J].控制理论与应用,2009,26(3):256-261.
[12]杨兆欣,杜红棉,范锦彪,等.基于广义最小二乘法加速度传感器的动态建模[J].传感技术学报,2009,22(2):195-198.
[13]厉玉鸣,马召坤,王晶,等.自动控制原理[M].化学工业出版社,2005:48-51.
[14]轩春青,轩志伟,陈保立,等.基于最小二乘与粒子群算法的压力传感器动态补偿方法[J].传感技术学报,2014,27(10):1363-1367.
[15]吴键,张志杰,王文廉,等.传感器动态补偿滤波器及其硬件实现方式研究[J].传感技术学报,2012,25(1):67-71.
[16]段丽玮,吴志华,徐志伟,等.基于ARX模型的飞机尾翼压电结构系统辨识研究[J].压电与声光,2008,30(6):760-762.
[17]Rao Y N,Erdogmus D,Rao G Y,et al.Fast Error Whitening Algorithms for System Identification and Control[C]//Proc NNSP,Toulouse,France,Sept.2003:309-318.

赵宁宁(1989-),女,河北沧州人,硕士研究生,主要研究方向为加速度传感器动态补偿,1406587603@qq.com;

王建林(通讯作者)(1965-),男,陕西西安人,现为北京化工大学教授,主要研究方向为复杂工业过程智能检测与传感技术、智能测控系统等,wangjl@mail.buct. edu.cn。
A Dynamic Error Compensating Method Based on High-Order Compensator for Accelerometer*
ZHAO Ningning,WANG Jianlin*,WEI Qingxuan,YU Tao,ZHAO Liqiang
(College of Information Science and Technology,Beijing University of Chemical Technology,Beijing 100029,China)
The dynamic characteristics of accelerometer play an important role in dynamic measurement.In order to improve the dynamic characteristics of the accelerometer and reduce measurement error,a dynamic compensation method based on high-order compensator is proposed.The dynamic model of acceleration is built using calibration data,and the compensator’s order is determined according to the system’s poles.Error Whiting Calculation(EWC)algorithm is used to identify the parameters of the compensator.The experimental results show that the high-order dynamic compensator,compared with the low-order compensator,has some advantages such as overshoot,arriving stable time and residual,and all of these indicators are reduced.
acceleration sensor;higher-order compensator;ARX model;EWC parameter identification
TH824
A
1004-1699(2016)08-1186-07
EEACC:7230;7230E10.3969/j.issn.1004-1699.2016.08.011
项目来源:国家重大科学仪器设备开发专项项目(2012YQ090208)
2016-01-20修改日期:2016-03-21

