GLONASS和GPS广播星历参数及拟合算法分析

肖琴琴，崔先强，周忠于，聂智平，黄长军，胡丽敏

(1.湖南城市学院 市政与测绘工程学院，湖南 益阳　413000；2.中南大学 地球科学与信息物理学院，湖南 长沙　410083)



GLONASS和GPS广播星历参数及拟合算法分析

肖琴琴1，崔先强2，周忠于1，聂智平1，黄长军1，胡丽敏1

(1.湖南城市学院 市政与测绘工程学院，湖南 益阳413000；2.中南大学 地球科学与信息物理学院，湖南 长沙410083)

为了进一步为我国北斗卫星导航系统的星历参数设计提供借鉴，着重对格洛纳斯和全球定位系统的广播星历参数及拟合算法进行了对比研究，结果表明：同一组精密星历拟合出的全球定位系统的星历参数得到的卫星坐标精度相对较高；而拟合出的格洛纳斯星历参数在求解卫星坐标的速率方面有优势。

GLONASS；星历参数；拟合算法；GPS

0　引言

目前，全球卫星导航系统(global navigation satellite system，GNSS)已深入至社会各领域，建立和发展自主的北斗卫星导航系统(BeiDou navigation satellite system，BDS)关系到我国的国防安全和经济建设的发展。BDS现已发展至第二代，处于高速发展的阶段，但要进入国际标准是一项长期而又艰巨的任务，尤其是进入国际民航标准，这需BDS建设者、民航界及工业界的共同努力。那么，在其发展中必不可少要借鉴其他导航定位系统进行完善。作为当前4大导航定位系统之一的全球定位系统(global positioning system，GPS)是全球出现最早的导航定位系统，在各个行业得到了广泛应用，在我国的导航市场中一直独占鳌头，现有卫星31颗，预计在2015年再发射两颗卫星，还将建设GPS III包括4个民用新频段，2020年实现新一代星座现代化。格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)虽然在发展过程中因经济问题影响了其发展，但经济复苏后其功能逐渐恢复步入现代化的轨道，目前正在蓬勃发展中，预计在2015年至2016年发射9颗GLONASS-M卫星，未来还将有GLONASS-K卫星，引入搜索和救援活动的有效载荷[1]。针对美国声称从2014-05-31起暂停俄国GLONASS信号站在美国境内运转的表示，俄国曾回应将从2014-06-01起暂停其境内的美国GPS信号站的运转[2]，由此可见俄罗斯GLONASS的实力。因此GPS和GLONASS的特性和发展是值得探讨的。

由于GPS和GLONASS系统的主要功能是进行定位导航，而卫星广播星历参数及拟合算法的设计作为导航定位系统的一项重要技术，它的精度、可靠及高效性都会对导航定位的性能产生直接的影响，因此，开展GPS和GLONASS广播星历参数及其拟合算法的研究具有一定的价值，它将为BDS的星历参数设计提供一定的依据。目前已有很多文献阐述了GPS卫星坐标和星历参数的计算[3-6]，但关于GLONASS卫星坐标和星历参数[7]计算的研究相对来说少些。综上所述，本文对GPS和GLONASS广播星历参数及参数的拟合算法进行了对比研究。

1　GLONASS广播星历参数及拟合算法

1.1GLONASS广播星历参数及用户算法

GLONASS广播星历参数由卫星的位置、速度及日月摄动加速度构成，与GPS广播星历参数完全不一样，它主要是利用地球、日月和卫星之间很小的几何关系变化来进行设计的。目前GLONASS卫星坐标的计算大多数是采用数值积分的方法，如龙格库塔积分法、欧拉积分法、阿达姆斯积分法等，其中龙格库塔法[8-9]应用得最多。下面简单地介绍利用四阶龙格库塔积分法计算GLONASS卫星的坐标、速度及加速度。

首先给出GLONASS卫星在PZ-90坐标系中的加速度公式[10-11]为：

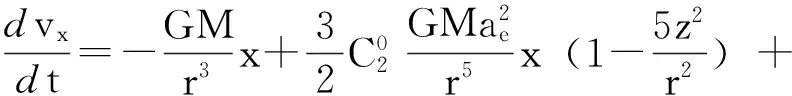
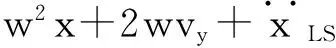
(1)

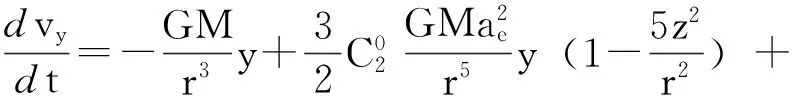
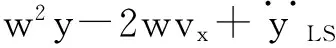
(2)

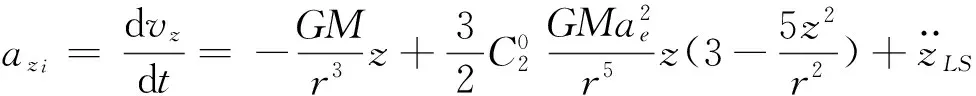
(3)

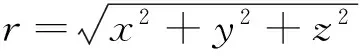
将ti时刻的加速度用函数形式表示为：

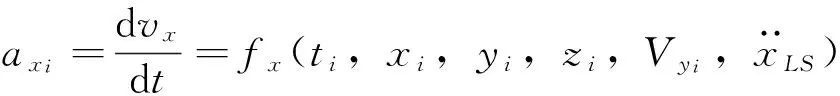
(4)

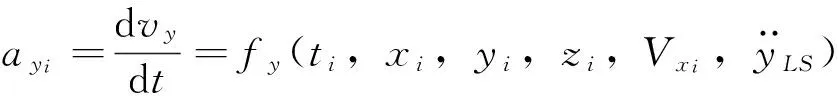
(5)

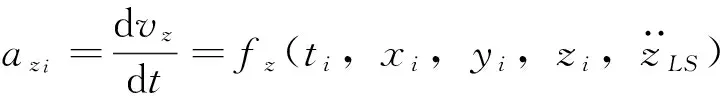
(6)

由于积分时间较短，可忽略卫星与日月短期内相对运动的影响，即在GLONASS广播星历文件中30 min内，可把日月摄动加速度看成常量[12]。观测时刻的日月摄动加速度可由距观测时刻最近的参考历元星历参数得到，而参考历元的星历则直接从GLONASS导航文件中读取。以距观测时刻tk最近的参考历元t0的星历参数作为初始的状态，即可求得tk观测瞬间卫星的坐标、速度及其加速度向量。

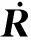
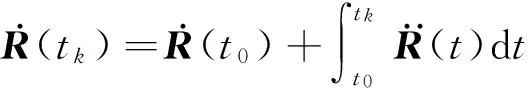
(7)

(8)

通过以上2次积分即可求出任意观测时刻卫星的坐标值。

本文采用的积分方法为四阶龙格库塔积分法，过程简述如下：

1)计算出积分所需的步数。确定一个步长后不能保证所得的步数一定为整数，如存在不足一个步长的部分时就分开处理。假定得出的步长数为n，不足一个步长的部分为Δh，参考时刻为t0，步长为h。

2)根据步长数n由龙格库塔法积分得出to+nh时刻的卫星坐标及速度。

3)对剩下的步长Δh进行积分求得观测时刻的卫星坐标和速度。

下面用公式的形式进行描述，以古典形式的四阶龙格库塔法为例。

首先以参考时刻的卫星坐标和速度作为一个基础，按照式(7)及式(8)，一个步长h后得：

M1j=f(ti,Pi,Vi,a)；

(9)

N1j=Vi；

(10)

M2j=f(ti+h/2,Pi+N1jh/2,Vi+M1jh/2,a)；

(11)

N2j=Vi+M1jh/2；

(12)

M3j=f(ti+h/2,Pi+N2jh/2,Vi+M2jh/2,a)；

(13)

N3j=Vi+M2jh/2；

(14)

M4j=f(ti+h,Pi+N3jh,Vi+M3jh,a)；

(15)

N4j=Vi+M3jh/2；

(16)

Vj+1=Vi+h(M1j+2M2j+2M3j+M4j)/6；

(17)

Xj+1=Xj+h(N1j+2N2j+2N3j+N4j)/6。

(18)

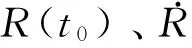
1.2GLONASS广播星历参数的拟合算法

对于GLONASS卫星，其广播星历及用户算法已有很多文献介绍，但参数拟合算法介绍得较少。本文在此简单介绍利用GLONASS卫星的精密星历内插出卫星的位置，再求得参考时刻GLONASS卫星广播星历参数的过程。

首先读取GLONASS精密星历中卫星的历元及坐标，选定其中一颗卫星的某一个参考历元，利用距离参考时刻1h之内的观测数据，采用拉格朗日插值法内插出距离参考历元0.5h之内各观测时刻的卫星坐标，观测间隔为1min，以这些内插值作为卫星位置的真值。然后求取卫星的速度和加速度，根据参考文献[13]可知，对于GLONASS卫星，运用数值差分法，结合卫星本身的特性，采用一阶中心差分器可得满足精度要求的卫星速度和加速度。

拉格朗日插值的基本原理在许多文献当中已有介绍[14-16]，本文在此略做阐述：

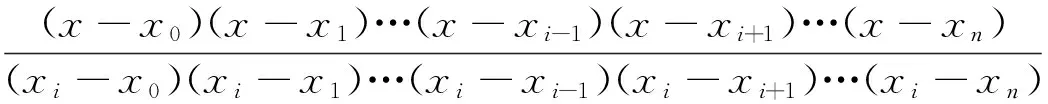
(i=0,1,2…n)。

(19)

从式(19)中可看出：当j=i时，li(xj)=1；当j≠i时，li(xj)=0。

根据卫星坐标精度选择插值阶数n，利用n+1个插值点内插出任意观测时刻卫星的坐标。一般来说，在求取观测时刻的坐标时，时刻处于插值时段的中间可得较高的精度；因为拉格朗日插值在两端容易出现龙格现象[14]，使得卫星坐标精度降低。

由数值差分法求卫星速度和加速度的公式为：

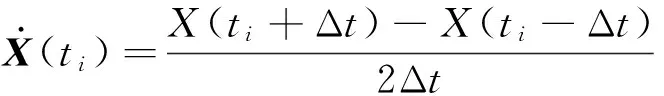
(20)

(21)

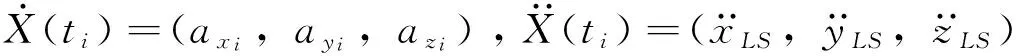
w2x+2wvy)；

(22)

(23)

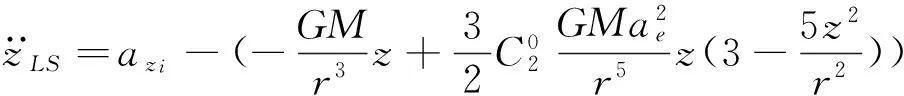
(24)

由上述过程即可求得参考历元的广播星历参数值。

2　GPS广播星历参数及拟合算法

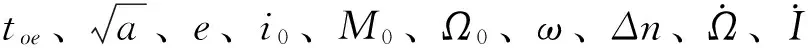
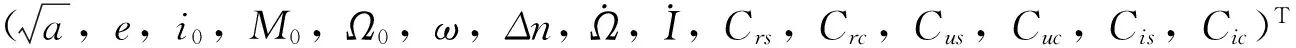
(25)

Yj=Yj(X,t)。

(26)

式中：X为参考历元时刻的15个广播星历参数，Yj为一个观测量，即卫星的一个位置分量，观测量的个数N≧15。若Xi为第i+1次迭代的初值，将方程式(26)线性化，略去二阶及其以上的高阶项，在所给初值处展开可得

(27)

其中：

lj=Yj-Yj(Xi,t)；

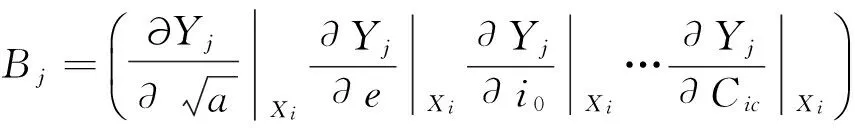
则式(27)可写为

V=BδXi+1-L。

(28)

式中：V为观测方程的残差；B为观测量对广播星历各参数的偏导数组成的误差方程系数矩阵；δXi+1为广播星历参数的改正值；Y(Xi,t)是通过Xi计算出的卫星位置近似值[3]。

通过上述过程即可求得参考历元的广播星历参数值。

3　计算与分析

本文的算例采用2014-11-11GLONASS的PRN02号卫星T00：04：00—T00：08：00之间的精密星历，利用拉格朗日插值法内插出GLONASS卫星轨道数据，采样间隔为1min，分别拟合出GLONASS和GPS的广播星历参数估值，由于GLONASS和GPS卫星的坐标不在同一坐标系下，在拟合GPS星历参数时采用的是经过转换的WGS84坐标。再运用此估值来分别计算其向前向后均0.5h的卫星位置，采样间隔也为1min，以卫星的内插轨道作为真值进行比较。为了验证GLONASS和GPS的广播星历参数对坐标的影响，以更好地对各系统广播星历参数进行评估，本文采用了3种方案进行对比：

方案1：采用2h的GLONASS精密星历内插出距参考时刻0.5h之内的GLONASS坐标，间隔1min，用之拟合GLONASS广播星历参数的估值，再以此估值计算出卫星位置，间隔1min，并与卫星内插轨道进行对比；

方案2：利用4h的GLONASS精密星历插值离参考时刻0.5h之内的GPS坐标，拟合出GPS广播星历参数后再计算出卫星位置，并进行对比；

方案3：应用2h的GLONASS精密星历内插距参考时刻0.5h之内的GPS坐标，以之拟合GPS广播星历参数，积分出卫星坐标再进行比较。

本算例使用用户距离误差(userrangingerror，URE)描述GLONASS、GPS广播星历参数拟合算法的精度，得出的计算结果如表1所示。

由表1的实验数据可看出：

1)方案1利用GLONASS广播星历参数计算的卫星轨道，其URE都达到分米级以下，越靠近参考时刻精度越高，可达cm级甚至mm级。距参考时刻15min之内卫星坐标的URE值都可达cm级，而在15～30min之内则大部分达到了dm级。这说明选择距观测时刻15min之内的参考时刻星历参数计算卫星坐标可达到较高精度。

2)方案2和方案3是采用GPS广播星历16参数计算的卫星坐标，其URE绝大部分都可达mm级，甚至可达次mm级。它的精度是呈现一个渐变的过程，在方案2和方案3中卫星轨道的精度变化趋势是由高至低，再至高至低不停地来回变化；但总的特征是方案2中的精度普遍较高，都达到了mm级甚至次mm级，而方案3中距参考时刻越近精度越高，达到了mm级，越远精度越低，有些达到了cm级。这说明采用GPS广播星历参数求得的卫星坐标具有较高的精度。

3)方案1与方案2、方案3进行对比可知，用GLONASS广播星历参数求得的卫星轨道坐标精度要低于由GPS广播星历参数计算出的卫星坐标精度。这是因为GPS广播星历参数利用了轨道摄动的基本特征，更能反应轨道变化的实际情况，而GLONASS广播星历参数主要是简单地利用地球、日月和卫星之间很小的几何关系变化，但利用GLONASS广播星历参数计算卫星坐标更加简单快捷，可提高速率。

4)对方案2和方案3的结果进行分析可看出：用4h的精密星历内插的坐标来拟合星历参数，再用来计算卫星坐标，比用2h具有更高的精度。这是因为在利用拉格朗日插值法内插轨道时，使插值时刻位于拟合弧段的中间能得到精度更高的坐标。同时也说明了用来拟合广播星历参数的卫星位置的精度是非常重要的。

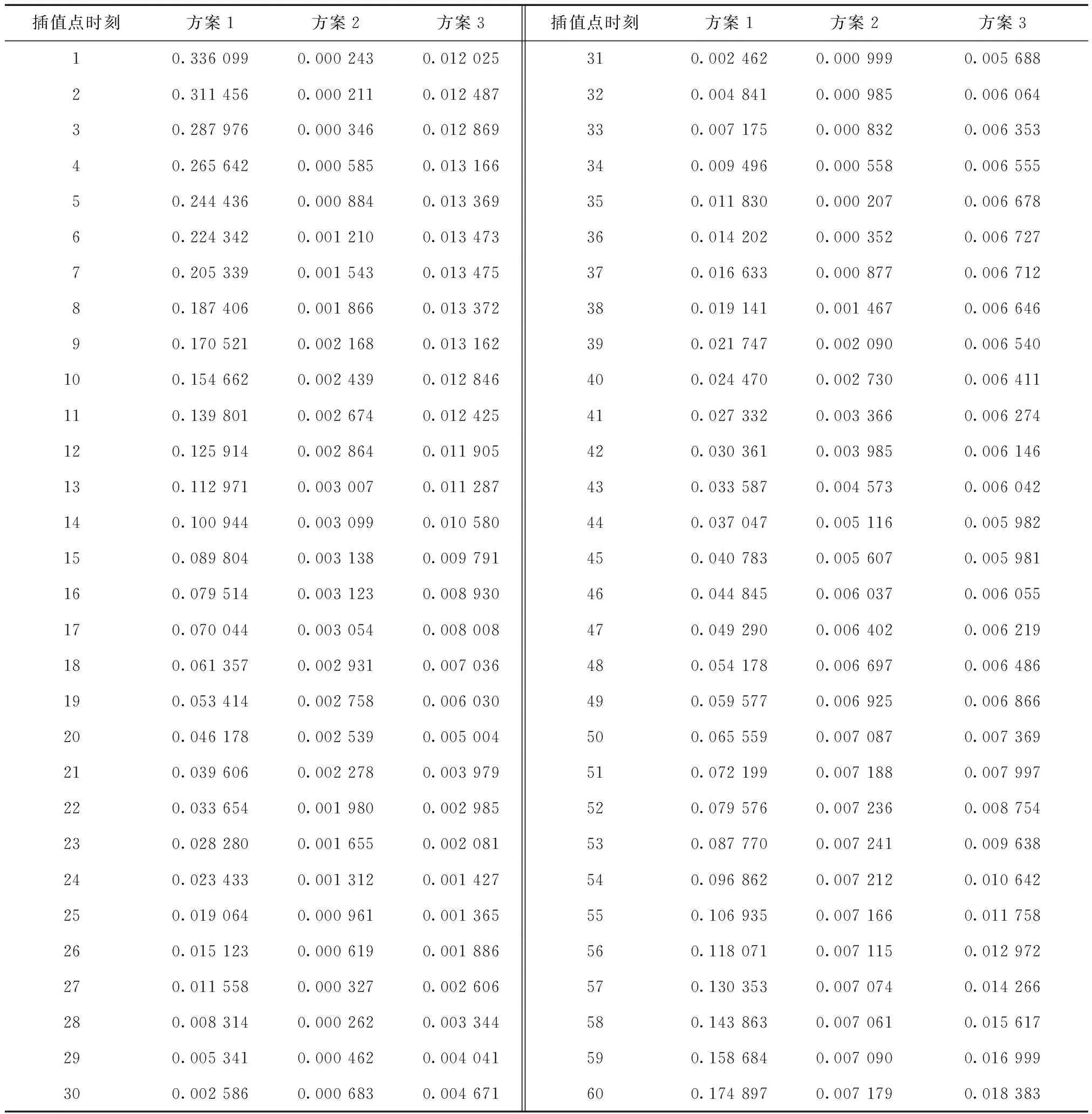
表1　GLONASS、GPS广播星历参数的拟合精度　m

4　结束语

本文通过对GLONASS和GPS广播星历参数及拟合算法的比较，得到如下结论：

1)GLONASS广播星历参数不适合于进行较长时间的外推，要保证cm级的精度则需使积分时间控制在15 min之内。

2)与GLONASS相比，外推时间对GPS广播星历参数的精度影响较为缓慢，即使是距参考时间30 min也能获得mm级的精度。

3)根据用户对导航定位精度的要求来选择卫星导航系统，若要求精度一般而计算速度要快的可选择GLONASS系统；而对精度要求较高，对计算时间要求不高则可选择GPS系统，当对精度和时间都有较高要求时可选择GPS/GLONASS组合系统来进行定位导航。

4)在利用精密星历内插的卫星轨道拟合星历参数时，应尽量保证内插出的坐标处于拟合弧段的中间，可使最终得到的卫星坐标精度更高。

[1]佚名.全球四大导航系统齐聚中国最关心什么?[J].全球定位系统，2015，40(3)：97.

[2]杨宇光.如果没有格洛纳斯，俄敢和美国叫板吗?[N].中国航天报，2014-05-17(1).

[3]肖琴琴，崔先强，贾小林，等.GPS广播星历参数及拟合算法的性能比较[J].大地测量与地球动力学，2014，34(1)：92-95.

[4]The National Coordination Office for Space-Based Positioning，Navigation，and Timing.GPS interface control document：IS-GPS-200[S/OL].[2015-01-26].http://www.gps.gov/technical/icwg/IS-GPS-200G.pdf.

[5]崔先强，焦文海，贾小林，等.GPS广播星历参数拟合算法[J].测绘学院学报，2004，21(4)：244-246.

[6]徐绍铨，张华海，杨志强，等.GPS测量原理及应用[M].3版.武汉：武汉大学出版社，2008：40-42.

[7]Coordination Scientific Information Center.GLONASS interface control document [EB/OL].(1992-02-02)[2015-01-26].gauss.gge.unb.ca/GLONASS.ICD-98.pdf.

[8]柯福阳，王庆，潘树国.自动积分步长的GLONASS卫星轨道龙格库塔积分法[J].东南大学学报：自然科学版，2010，40(4)：755-759.

[9]卢祥，袁运彬，蒋振伟.基于龙格库塔法的GLONASS轨道仿真研究[J].大地测量与地球动力学，2014，34(3)：137-141.

[10]葛奎，王解先.GLONASS卫星位置计算与程序实现[J].测绘与空间地理信息，2009，32(2)：137-140.

[11]李显，吴美平，张开东，等.导航卫星速度和加速度的计算方法及精度分析[J].测绘学报，2012，41(6)：816-824.

[12]贾小林，焦文海，吴显兵.GLONASS广播星历用户算法精度分析[J].测绘学院学报，2005,22(3)：160-162.

[13]翟瑞彩，谢伟松.数值分析[M].天津：天津大学出版社，2000：104-126.

[14]魏二虎，柴华.GPS精密星历插值方法的比较研究[J].全球定位系统，2006，31(5)：13-15.

[15]胡辉，徐璐超.GPS卫星轨道插值及拟合研究[J].河南师范大学学报：自然科学版，2009,37(5)：58-61.

[16]洪樱，欧吉坤，彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报·信息科学版，2006，31(6)：516-518.

Analysis on broadcast ephemeris parameters and fitting algorithms of GLONASS and GPS

XIAO Qinqin1，CUI Xianqiang2，ZHOU Zhongyu1，NIE Zhiping1，HUANG Changjun1，HU Limin1

(1.College of Municipal and Mapping Engineering,Hunan City University, Hunan Yiyang 413000,China;2.School of Geosciencesand Info-physics, Central South University, Changsha 410083, China)

In order to provide more references for the design on satellite broadcast ephemeris parameters of China's BDS，the paper comparatively studied on the satellite broadcast ephemeris parameters and the fitting algorithms of GLONASS and GPS.Result showed that the accuracy of satellite coordinates calculated by GPS ephemeris parameters fitted by the same precise ephemeris with GLONASS would be relatively higher，while the rate of solving satellite coordinates gained by GLONASS ephemeris parameters would have an advantage over that by GPS.

GLONASS;ephemeris parameters;fitting algorithm；GPS

2015-03-29

湖南城市学院科技计划项目(2014xj10)；地理信息工程国家重点实验室开放基金项目(SKLGIE2013-M-2-4)；中国博士后科学基金项目(2013M540641)。

肖琴琴(1988—)，女，湖南衡阳人，硕士，讲师，研究方向为GNSS卫星数据处理与应用。

10.16547/j.cnki.10-1096.20160305.

P228

A

2095-4999(2016)03-0020-06

引文格式：肖琴琴，崔先强，周忠于，等.GLONASS和GPS广播星历参数及拟合算法分析[J].导航定位学报，2016，4(3)：20-25.(XIAO Qinqin，CUI Xianqiang，ZHOU Zhongyu，et al.Analysis on broadcast ephemeris parameters and fitting algorithms of GLONASS and GPS[J].Journal of Navigation and Positioning，2015，4(3)：20-25.)