星历误差的低次曲面模型改正方法

任超超，李灵巧，2，蔡成林，杨辉华，2

(1.桂林电子科技大学 电子工程与自动化学院，广西 桂林　541004；2.北京邮电大学 自动化学院，北京　100876；3.桂林电子科技大学 广西精密导航技术与应用重点实验室，广西 桂林　541004)



星历误差的低次曲面模型改正方法

任超超1，李灵巧1，2，蔡成林3，杨辉华1，2

(1.桂林电子科技大学 电子工程与自动化学院，广西 桂林541004；2.北京邮电大学 自动化学院，北京100876；3.桂林电子科技大学 广西精密导航技术与应用重点实验室，广西 桂林541004)

针对广播星历误差限制了广域差分定位精度的问题，提出了星历误差的低次曲面模型改正方法。通过6个均匀分布的差分站与5颗由GEO、MEO和IGSO卫星组成的导航星座对该方法进行仿真验证，结果表明低次曲面模型法能将星历误差改正到较高的精度。同时，针对6个差分站改正效果均匀性较差的问题，提出了11个差分站优化布局方案，使得低次曲面模型法的改正效果更加均匀，定位精度达到1 m以内。该方法对广域差分定位精度有良好的改正效果，而且在GEO、MEO和IGSO卫星导航星座中具有通用性，对我国卫星导航星基增强系统建设有一定的参考价值。

星历误差；广域差分；曲面模型；优化布局

0　引言

广播星历是由全球卫星导航系统(global navigation satellite system，GNSS)的地面控制中心确定和提供的，经卫星向全球所有用户公开播发的一种预报星历，其精度较差[1]。目前全球定位系统(global positioning system，GPS)的广播星历误差在3～5 m，广播星历误差限制了GPS的定位精度[2]。文献[3]提出了星钟和星历误差分离的广域差分方法，将星钟和星历分离解算，有效地降低了精度衰减因子(dilution of precision，DOP)值，提高了差分用户的定位精度。本文在这种方法的基础上提出一种星历误差的低次曲面模型改正方法：在空间上将主站(与卫星时间严格同步)观测的伪距误差分配给星钟作为星钟误差，通过一站式改正方法[3]消除；然后将外场多个副站(与卫星时间不严格同步)观测的伪距误差扣除星钟误差后的剩余量分配给星历作为星历误差，在一定范围的服务区内建立曲面模型；并将曲面模型的几个参数广播给用户，用户根据自己所处的经纬度，利用曲面模型参数计算出所在位置的剩余星历误差并直接改正。

1　星历误差及其空间分布

在卫星导航星基增强系统中，各差分站时间保持完全同步非常困难。当前采用卫星双向时间频率传递技术[4]，各站之间仍会有0.3～1 ns的时间同步误差；如果采用理想情况的矢量差分原理解算，站钟时间同步误差会吸收为星历误差，受逆定位DOP的误差放大[5]影响，星历改正数的解算精度并不高，目前GPS的星历改正精度只能达到2.5 m[6]。

为了获得更高的差分解算精度，文献[7]提出一种星钟和星历误差相对改正方法，这种改正并不是将某颗卫星的星历误差真正完全分离，而是将相对于基准星的星历误差分配给这颗星，它实质上是同一副站对不同卫星的径向星历误差的相对量。外场差分站的伪距误差经过电离层、对流层、伪码噪声平滑等误差预处理[8-9]，再经过星钟误差一站式改正后，可认为是由星历误差和站钟偏差2部分组成的，其中站钟偏差可用星间单差法[10]消除，最后剩余量为星历误差。

然而星钟误差一站式改正法只能保证主控站视向星历误差消除，对于非主控站，星历误差会随着主控站和用户之间距离的增加而增加。星历误差最终会反映到用户的测量结果上；因此可以将星历误差投影到站星矢径上进行分析，用星历误差的用户等效距离误差(user equivalent range error，UERE)来表示。本文进一步分析了4颗卫星星历误差的UERE空间分布规律，如图1所示。

图1　星历误差的UERE空间分布

卫星1、4、5为中地球轨道(medium Earth orbit，MEO)卫星，卫星2为地球静止轨道(geosynchronous Earth orbit，GEO)卫星，卫星3为倾斜地球同步轨道(inclined geosynchronous satellite orbit，IGSO)卫星；其中卫星1作为基准星不改正，主控站为西安站(110°E，34°N)。从图1中可以看出：1)在74°E～138°E与9°N～49°N服务区内对不同的卫星，与主控站处于同一纬度但经度不同的用户，其径向星历误差的UERE在1.5 m以内，与主控站处于同一经度但纬度不同的用户，其径向星历误差的UERE在1 m以内；2)主控站附近星历误差最小，距离主控站越远星历误差越大，服务区内星历误差的大小与用户所处的经纬度有关；3)在74°E～138°E与9°N～49°N服务区内，径向星历误差在空间上呈现一个平滑的曲面形状。

2　低次曲面模型法原理

从图1给出的星历误差的空间分布可以看出，星历误差在空间上能用低次曲面近似表征。基于这一点，本文提出利用低次曲面模型改正星历误差：利用多个差分站的星历误差，在一定的服务区内建立低次曲面模型；并将曲面模型的几个参数广播给用户，用户根据自己所处的经纬度，利用曲面模型参数计算出所在位置的星历误差并直接改正。

低次曲面模型可表征为：

(1)

(2)

(3)

a4B2+a5L3+a6B3；

(4)

a4LB+a5B2+a6L3+a7B3；

(5)

a5B2+a6L3+a7BL2+a8LB2+a9B3。

(6)

式(1)至(6)中：V表示星历误差；L和B分别表示经度和纬度；ai(i=0，1，2，…,9)为第i个系数阵，迭代解为

(7)

式中Δρ表示一站式相对改正消除星钟误差后的剩余星历误差，其模型对应的迭代矩阵H有6种形式，式(8)以模型3为例表示为

(8)

式中：H的行数等于差分站数量；Ln和Bn分别表示差分站n的经度和纬度。

根据模型参数计算用户所在位置的星历误差为

(9)

式中Hu表示用户所在位置对应的迭代矩阵，有6种形式，式(10)以模型3为例表示为

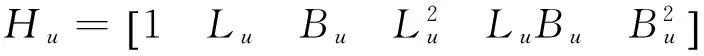
(10)

式中Lu和Bu分别表示用户所在位置的经度和纬度。

改正后的残余星历误差

ε=Δρ-V。

(11)

3　实验与结果分析

3.1曲面模型改正效果

为了验证上述6种低次曲面模型的改正效果，本文利用6个均匀分布的差分站(西安、长春、上海、乌鲁木齐、三亚、拉萨)与5颗由GEO、MEO和IGSO卫星组成的混合星座进行实验。卫星1、4、5选用GPS中的MEO卫星(PRN7、PRN8、PRN10)，卫星2、3分别选用北斗卫星导航系统中的GEO卫星(PRN3)和IGSO卫星(PRN9)；这5颗卫星在北京时间04∶00—05∶00对这6个差分站都是可视的，其中卫星1作为基准星不改正。实验数据中卫星1、4、5的真实星历用国际GNSS服务组织发布的精密星历代替，卫星2、3的真实星历用武汉大学GNSS研究中心发布的精密星历代替，广播星历以及伪距观测值来自中科院国家授时中心的双频接收机，采样频率为5min，通过内插让真实星历和广播星历均为1s一次。在74°E～138°E与9°N～49°N格网范围内，伪距误差经过电离层误差改正、对流层误差改正、伪码噪声平滑、星钟误差一站式改正、站钟偏差消除后，剩余量为星历误差，通过曲面模型法在经度和纬度方向每隔4°计算一个改正后的残余星历误差ε，用ε的最大值Max、最小值Min和平均数E表征模型的精度，用ε的标准差(来表征模型改正效果的均匀性。实验结果如表1所示。

从表1可以看出：1)对GEO、MEO和IGSO这3种混合星座，曲面模型改正后的残余星历误差的均值都小于0.1 m，误差的标准差都小于0.1 m，这表明低次曲面模型法达到了较高的精度；2)模型3改正后GEO、MEO和IGSO这3种混合星座卫星的残余星历误差的最大值、最小值、平均数和标准差的绝对值都是最小的，这表明模型3的改正效果最好，其中，残余星历误差小于0.15 m，误差的均值小于0.06 m，误差的标准差小于0.06 m。图2给出模型3改正后的残余星历误差空间分布，可以直观地看出模型3的改正效果。

表1　曲面模型改正后的残余星历误差　m

图2　模型3改正后的残余星历误差空间分布

3.2差分站优化布局

利用6个均匀分布的差分站建立的低次曲面模型3虽然能将星历误差的均值改正到0.06 m；但是误差的标准差大于均值，残余星历误差的最大值达到0.15 m，说明改正效果不够均匀：因此需要考虑差分站优化布局[8-10]。

从图2可以看出，由6个均匀分布的差分站建立的低次曲面模型改正后的视向残余星历误差较大的区域大约在(100°E～120°E，20°N～40°N)和(60°E～80°E，10°N～20°N)之间；因此考虑在包头、喀什、长沙、昆明和东沙群岛各增加1个差分站(对这5颗卫星可视)，由11个差分站优化布局建立低次曲面模型，选择改正效果最好的模型3进行仿真实验。实验结果如表2所示。

表2　差分站优化布局后的曲面模型改正结果　m

从表2可以看出：对GEO、MEO和IGSO这3种混合星座，11个差分站优化布局建立的低次曲面模型能将星历误差改正到0.09 m以内，误差的均值在0.05 m以内，误差的标准差小于0.02 m。图3给出差分站优化布局后的曲面模型改正效果，可以直观地看出曲面模型的改正精度得到很大提升，改正效果非常均匀。

图3　差分站优化布局后的曲面模型改正效果

图4用靶图给出11站差分前后的主站(西安站)、副站(以长沙站为代表)和2个网内验证用户(武汉和成都)的定位偏差。靶心表示测绘位置；与靶心的距离表示定位偏差。可以看出：差分前的定位偏差在10～30 m之间；经过电离层、对流层、伪码噪声平滑、星钟误差一站式改正、星历误差的低次曲面模型改正后的定位偏差在1 m以内。

图4　定位偏差

4　结束语

通过建立低次曲面模型与差分站优化布局，可以得出如下结论：

1)经过星钟误差一站式改正后，星历误差能够用本文提出的低次曲面模型法改正，其中二次曲面模型的改正效果最好。

2)低次曲面模型法的改正效果与地面差分站布局有很强的相关性，本文提出的11个差分站优化布局方案建立的曲面模型可以将中国陆地和近海区域的径向星历误差改正到0.09 m以内，误差的均值在0.05 m以内，误差的标准差小于0.02 m，改正效果非常均匀，差分定位偏差修正到1 m以内。

3)本文提出的方法在MEO、GEO和IGSO卫星导航星座中具有通用性，对我国卫星导航星基增强系统建设有一定的参考价值。

[1]焦海松，王红芳，姚飞娟.卫星星历误差对 GPS 定位精度的影响与分析[J].全球定位系统，2009，34(1)：24-28.

[2]周立. GPS 广播星历误差影响诊断与预测模型研究[J].测绘科学，2005，30(4)：37-38，4.

[3]CAI Chenglin，LI Xiaohui，WU Haitao. An analysis of the wide area differential method of geostationary orbit satellites[J]. Science in China Series G：Physics，Mechanics and Astronomy，2009，52(2)：310-314.

[4]BAUNCH A. Time and frequency comparisons using radiofrequency signals from satellites[J]. Comptes Rendus Physique，2015，16(5)：471-479.

[5]王泽民，孟泱，伍岳，等. GPS、Galileo 及其组合系统导航定位的DOP值分析[J].武汉大学学报·信息科学版，2006，31(1)：9-11，38.

[6]曹新运，王坚，刘超. DOP值进行 GNSS 相对定位预报的适用性研究[J].大地测量与地球动力学，2013，33(1)：81-85.

[7]CAI Chenglin，LI Xiaohui，WU Haitao. A virtual reference satellite differential method on relative correction of satellite ephemeris errors[J].Science in China Series G：Physics，Mechanics and Astronomy，2010，53(12)：2300-2306.

[8]王甫红.高精度星载GPS实时定轨卡尔曼滤波模型[J].武汉大学学报·信息科学版，2010，35(6)：653-656.

[9]易重海，陈永奇，朱建军，等.一种基于 IGS 超快星历的区域性实时精密单点定位方法[J].测绘学报，2011，40(2)：226-231.

[10]刘吉华，欧吉坤，孙保琪，等.基于星间单差法的GEO卫星精密定轨[J].武汉大学学报·信息科学版，2011，36(1)：24-28.

Low-order surface model correction for ephemeris errors

REN Chaochao1，LI Lingqiao1，2，CAI Chenglin3，YANG Huihua1，2

(1.School of Electronic Engineering and Automation，Guilin University of Electronic Technology，Guilin，Guangxi 541004，China；2.School of Automation，Beijing University of Posts and Telecommunications，Beijing 100876，China；3.Guangxi Key Laboratory of Precision Navigation Technology and Application，Guilin University of Electronic Technology，Guilin，Guangxi 541004，China)

Aiming at the problem that the positioning accuracy of wide area differential system is limited by ephemeris errors，a method of low-order surface model correction for ephemeris errors was presented in this paper. Six evenly distributed differential stations and five satellites comprises GEO，MEO and IGSO were used in simulations. The results showed that this correction could achieve a high precision. Meanwhile，the positioning accuracy was corrected to one meter and the effect was more evenly by eleven optimized distribution differential stations. This method would have not only a high positioning accuracy but also versatility in a variety of GEO，MEO and IGSO satellite navigation constellation，and provide a reference for the construction of China’s satellite-based augmentation system of satellite navigation.

ephemeris errors；wide area differential；surface model；optimized distribution

2015-12-18

国家自然科学基金项目(61263028)；广西自然科学基金重点项目(2012GXNSFDA053027，2014GXNSFBA118280)；中国科学院时间频率基准重点实验室开放基金项目(Y000YR1S01)；桂林电子科技大学研究生教育创新计划资助项目(GDYCSZ201478)。

任超超(1991—)，男，安徽芜湖人，硕士研究生，研究方向为卫星导航与信息处理。

10.16547/j.cnki.10.-1096.20160301.

P228

A

2095-4999(2016)03-0001-06

引文格式：任超超，李灵巧，蔡成林，等.星历误差的低次曲面模型改正方法[J].导航定位学报，2016，4(3)：1-5,25.(REN Chaochao，LI Lingqiao，CAI Chenglin，et al.Low-order surface model correction for ephemeris errors[J].Journal of Navigation and Positioning，2016，4(3)：1-5,25.)