谋定而后动——论解析几何题的求解突破

叶　欣　 江用科

(北京工业大学附属中学，北京　100022)



谋定而后动
——论解析几何题的求解突破

叶欣 江用科

(北京工业大学附属中学，北京100022)

解析几何的本质是用代数方法研究图形的几何性质，体现了数形结合的重要数学思想．我们在教学中，要教给学生分析问题的基本方法：首先要明确题目中的几何问题是什么，然后分析几何要素，思考如何进行转化，最后再用坐标法进行推理、求解．

解析几何数形结合转化与化归思想

解析几何是高中数学的重要内容之一，在高考中占有重要地位．由于解析几何解答题综合性强，计算量大，因此是学生比较犯怵的一个考点，也是高考中拉开学生分数的题目，更是高三总复习中教师特别关注的一个专题．以北京高考为例，每年数学高考题的第19题基本都是有关解析几何的题目，命题也主要以直线与圆锥曲线的位置关系为背景．在高三总复习的过程中，笔者发现学生并不理解解析几何的本质，只是按照套路做题，有些学生甚至连图都不画，直接将直线方程与圆锥曲线方程联立起来，消元得到一元二次方程，再利用根与系数的关系，列出等式，然后寻找有用的条件进行分析，如果遇到稍微复杂的题就只能碰碰运气． 怎样改变这种现状呢？笔者就这个问题展开了深刻的思考，并在高三总复习的教学中进行了多种尝试．通过引导学生对题目的分析，让学生逐步理解解析几何的本质，从而体会数形结合思想；引导学生合理设计解题思路，体会转化和化归思想，进而轻松解题．

一、分析几何要素，进行数与形的转化

【案例分析】学生见到此题时，通常会设出直线l的方程，将其与椭圆方程联立，再利用P、Q两点关于原点对称这一特征，表示出P、Q两点的坐标．进而表示出|PF2|、|QF2|的长度，最终求出△PF2Q的面积．依照这个思路，求解的过程非常复杂，只有少部分学生能得出最终结果．

【解题过程】解：设椭圆的左焦点为F1，因为直线l过原点与椭圆交于点P,Q，由对称性可知，四边形PF1QF2是平行四边形，所以△PF2Q的面积等于△PF1F2的面积．

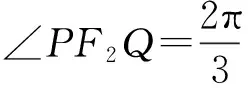
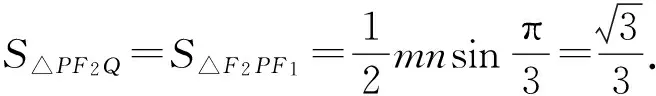
二、分析几何要素，进行多角度的转化

(Ⅰ)若直线l的方程为x+2y-1=0，求△OCD外接圆的方程；

(Ⅱ)判断是否存在直线l，使得C，D是线段MN的两个三等分点，若存在，求出直线l的方程；若不存在，说明理由．

解法一：假设存在直线l，使得C，D是线段MN的两个三等分点．

由题意，设直线l的方程为y=kx+m(km≠0)，M(x1,y1)，N(x2,y2)，

得(1+2k2)x2+4kmx+2m2-2=0，

所以Δ=16k2-8m2+8>0，

(*)

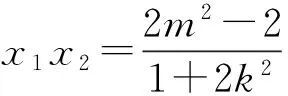
由C，D是线段MN的两个三等分点，得线段MN的中点与线段CD的中点重合．

由C，D是线段MN的两个三等分点，得|MN|=3|CD|．

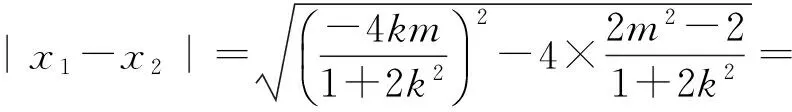
验证知(*)成立．

【教师引导与解题过程二】既然我们可以利用熟悉的中点解决问题，那是否可以将三等分点直接转化为中点呢？实际上C，D是线段MN的两个三等分点等价于|MD|=|DC|=|CN|，等价于C是DN的中点，且D是MC的中点，这样利用中点坐标公式就可以直接求解．

解法二：假设存在直线l，使得C，D是线段MN的两个三等分点．

由题意，设直线l的方程为y=kx+m(km≠0)，M(x1,y1)，N(x2,y2)，

得(1+2k2)x2+4kmx+2m2-2=0，

所以Δ=16k2-8m2+8>0，

(*)

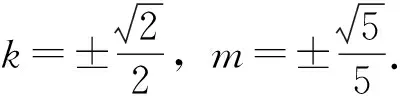
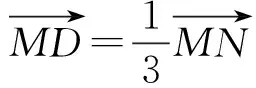
解法三：假设存在直线l，使得C，D是线段MN的两个三等分点．

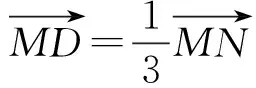
下同解法二．

【教师引导与解题过程四】上述三种解法都是先设出直线l的方程，进而表示出C，D的坐标，再将几何条件转化为代数问题，进行求解．求解本题是否还可以转变一下思路呢？抓住C，D是坐标轴上的点，M，N是椭圆上的点这两个条件，先设出C，D的坐标，再利用前面解法中转化好的几何条件表示出M，N的坐标，将其代入椭圆方程进行求解．

解法四：假设存在直线l，使得C，D是线段MN的两个三等分点．

由C，D是线段MN的两个三等分点，得C是DN的中点，且D是MC的中点，则M(-c，2d)，N(2c，-d)．

【案例总结】在高考中，解析几何的解答题常与三角函数、向量、函数、不等式等内容综合在一起考查，难度确实很大，如果我们能多花一些时间分析题目中的几何问题，合理转化题中涉及的几何要素，先确定可行的解题方案，再动笔进行计算，就能轻松攻克解析几何难关．

[1] 中华人民共和国教育部．普通高中数学课程标准(实验) [S]． 北京：人民教育出版社，2003．

[2] 章建跃． 人教A版高中数学课标教材中的解析几何[J]． 中学数学教学参考，2007(10)．

[3] 王先进． 高三数学复习要抓实三个环节[J]． 中学数学月刊，2013(10)．

[4] 张跃红． 合理设计追求高效[J]． 数学通报，2013(10)．

(责任编辑：李珺)