链接三个有效基点，实现概念的理性跨越

安徽合肥市巢湖市人民路小学西校区（238000） 魏胜生

链接三个有效基点，实现概念的理性跨越

安徽合肥市巢湖市人民路小学西校区（238000） 魏胜生

在小学数学教学中，数学概念是教学的重点，也是教学的难点。如何引领学生从感性顺利跨越到理性，这是教师亟待思考的问题。从三个基点入手，发展学生的数学思维，提升概念教学效率，实现可持续发展。

小学数学教学策略数学概念理性跨越

概念是思维的起点，是数学教学的核心。教师要巧妙设计教学活动，根据学生的已有学情，从学生的经验点、知识迁移点、核心点入手，沟通数学概念的内外关联。

一、链接经验点

根据建构主义理论，新知学习是基于学生已有经验的有效融合。教师要找准学生的已有经验，加强学生对抽象概念的感性体验，从而实现理性的跨越。

例如，教学“认识公顷”时，先让学生复习已经学过的面积单位。学生给出学过的面积单位“平方厘米、平方分米、平方米、公顷”，我针对其中的进率提出问题：“想一想，相邻的两个面积单位进率是多少？平方厘米和平方米之间的进率是多少？你发现了什么？”学生根据相邻的面积单位进率是100，得到平方米和公顷的进率为10000。此时我追问：“就平方米和公顷的进率是10000，你还能发现什么？”学生发现，在平方米和公顷之间应该还有一个面积单位——公亩。

我根据学生的已有经验，引导学生思考：1公亩的大小有多大？你怎么体会它大小？学生根据面积是1平方米的正方形的经验，认为1公亩就是边长为10米的正方形；还有学生认为，1公亩就是平方十米。根据学生的这一思路，我继续引导：1公亩叫平方十米，那么1公顷叫什么？学生得出，1公顷就是边长为100米的正方形，就是平方百米。根据平方米、平方十米、平方百米这几个逐渐升级的面积单位，学生由此推想出下一个最大的面积单位为平方千米。紧接着，我让学生根据这几个面积单位之间的进率，完成题目“1.8（ ）=180（ ）；400（ ）=0.4（ ）”由此，学生在巩固旧知的基础上，对公顷有了直观的理解。

教师借助学生的已有经验，从公亩顺利过渡到公顷，有效链接了长度单位和面积单位之间的关系，让学生对概念理解有了更深一层的提升。

二、链接迁移点

在概念教学中，教师要根据学生的实际情况，链接知识的迁移点，拓展数学课堂的思维空间。

例如，教学“公倍数和最小公倍数”时，我设计了习题：幼儿园里分糖果，要平均分给3个小组，正好分完；要平均分给4个小组，正好分完；这些糖果有多少个？学生根据这个问题中的已知条件，提出只要找出3和4的最小公倍数就可以。在这个基础上，我加了一个条件：“要平均分为6个小组，正好分完。这些糖果至少要有多少个？”有学生认为要找出3、4、6的最小公倍数，根据求两个数的公倍数的经验，可以先分别列举出3的倍数，4的倍数，6的倍数，然后由这三个数的倍数找出公倍数；有学生认为，可以将6的倍数列举出来，对照看看哪个是数字3和4的公倍数，然后找出最小的那个；有学生提出直接找出4和6的公倍数，因为6的倍数一定是3的倍数。以上三种方案，到底哪种最简便呢？经过讨论后学生得出，使用短除法更为有效。

教师从学生已有的知识经验入手，引导学生正向迁移，使学生对抽象的数学概念有了深入理解。

三、链接拓展点

在概念教学中，教师要立足概念的延伸和应用，链接概念的拓展点。

例如，教学“认识面积”时，面积和周长是学生容易混淆的两个概念，在理解时有必要进行区分。因而，我借助直观演示和动手操作，设计了两个活动。

活动一，出示图1，让学生观察哪一块涂色部分的面积比较大。学生认为面积一样大，因为都是6块小正方形组成。此时我增加了一个条件：如果每个小正方形的边长是1厘米，哪一块涂色部分的周长比较长？

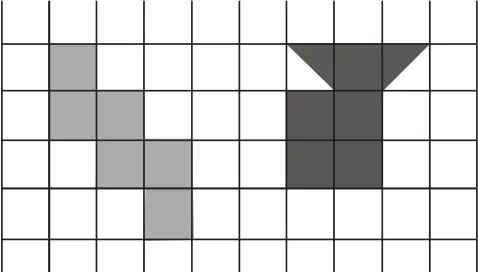
图1　

活动二，出示图2，让学生动手操作比较周长和面积。我将学生分成两组，要求一组学生看一个4格的图形，另一组学生看一个6格的图形，但这两个图形没有标准单位，比较哪个图形面积比较大。由此引发了学生的探究欲望：到底怎么进行面积大小的比较呢？这就为探究面积大小的比较奠定了基础。

图2　

教师在学生的最近发展区设计教学活动，通过比较学生发现了其中隐含的规律，提升了思维。

总之，在概念教学中，教师要有效链接学生的经验点、知识的迁移点和拓展点，以此实现从感性到理性的跨越，发展学生的数学能力。

（责编童夏）

G623.5

A

1007-9068（2016）23-086