遗传算法搜索雷达脉冲重复周期

华　瑶，孙晓闻

(南京电子技术研究所,　南京 210039)



·总体工程·

遗传算法搜索雷达脉冲重复周期

华瑶，孙晓闻

(南京电子技术研究所,南京 210039)

采用脉冲多普勒体制的雷达需发射多个不同重复周期(PRI)的脉冲组对目标进行探测。在雷达工程中一般采用穷举搜索的方法来优选PRI，计算量巨大。文中研究了遗传算法(GA)搜索雷达PRI方法，针对机载雷达探测空中目标的特点，以速度盲区和距离盲区联合最小作为适应度评价函数，搜索结果具备良好的探测清晰区。通过仿真示例说明了遗传算法搜索PRI的有效性，并对遗传算法的计算量进行了分析。与穷举搜索法相比，遗传算法大大减少搜索数目，可以快速搜索出满足工程要求的PRI组合，具备良好的工程适用性。

遗传算法; 脉冲重复周期; 盲区

0　引　言

机载雷达为了有效抑制杂波，提高检测能力，一般采用脉冲多普勒处理(PD)[1-2]技术。PD采用多组不同的脉冲重复周期(PRI)，根据一定的准则进行检测，常用的如：2/4、3/8准则[3-4]等。PRI组合的选择一般采用搜索的方法，但是PRI组合数目很大，如果采用穷举法搜索速度很慢。遗传算法(GA)[5-6]能够减小搜索的组合数目，大大加快搜索速度，可以快速搜索出满足工程要求的结果。

1　遗传算法搜索PRI

下面对遗传算法搜索PRI的详细过程进行介绍。

1.1编码

遗传算法最基本的编码方案是采用二进制编码，但二进制编码对于PRI的搜索来说有一定的局限性：(1) 不直观，需要经过编码与解码的过程，不能直接与解完间一一对应；(2) 个体中每个染色体取值范围的限定较麻烦；(3) 精度不好控制，小数点后的所需位数不好限定。而采用十进制编码可以有效地解决上述三个问题，因而本文采用的是十进制编码，直接利用PRI值作为个体的基因。

1.2个体取值范围的限定

一组较好的PRI，在整个要求的可选范围内分布均匀，如果产生初始种群时不加以控制，会产生某两个或几个PRI的值很接近的个体，这样的个体是不好的。因此，在产生初始种群时可以限定每个PRI的选取范围，这样就可以使每个个体的分布在整个PRI取值范围内分布得更加平均一些。本文对个体取值范围的限定方法如下：

假设要搜索的PRI的范围为[Tr min，Tr max]，Tr min为最小PRI，Tr max为最大PRI，要搜索的一组PRI为N个，分别为Tr1,Tr2,…,TrN，则两个PRI的平均间距ΔT为

(1)

假设第一个PRI与最后一个PRI的变化范围为C1·ΔT，C1为取值范围的限定系数，Tr1与TrN的取值范围为

Tr1=[Tr min,Tr min+C1·ΔT]

(2)

TrN=[Tr max-C1·ΔT，Tr max]

(3)

假设Tri,i=2,3,…,N-1的变化范围为C2·ΔT，其取值范围为

Tri=[Tr min+(Ni-1)·ΔT-C2·ΔT·Tr min+

(Ni-1)·ΔT+C2·ΔT]

(4)

这样，通过改变C1与C2的值就可以控制每个Tri的取值范围。通过图1可以直观地看出每个Tri的取值范围。

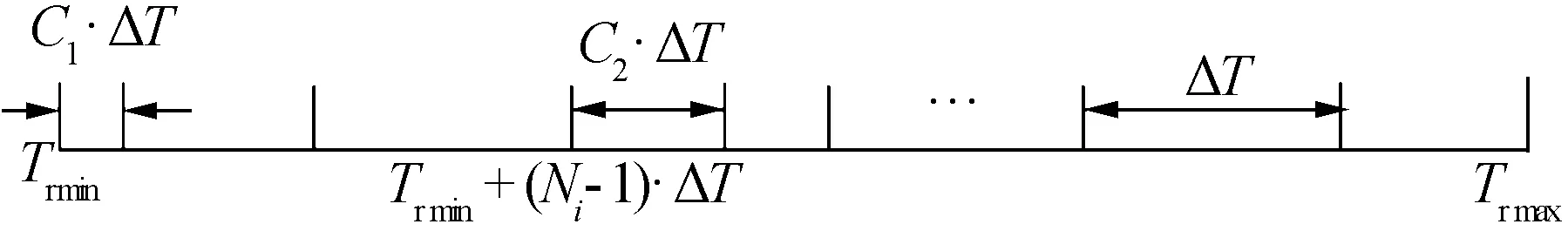
图1　个体取值范围的限定

1.3适应度评价

如何评价个体的适应度是遗传算法搜索PRI的一个关键问题[7]，适应度评价的合适与否直接关系到最终能否搜索出符合要求的结果。本文以速度清晰区为适应度函数，以速度清晰区最大为准则。选择速度清晰为适应度函数的原因如下：

(1)在工程中，速度上没有盲区是最重要的，因为距离始终都在变化，即使距离上存在一定的盲区，只要不大，经很短的时间目标就可跨越盲区，所以对检测影响不大。

(2)距离-速度二维清晰区最大是一种更好的搜索准则，但是二维清晰区的计算量很大，会极大减慢搜索速度，而且即使二维清晰区最大也不能保证速度清晰区最大。

(3)用清晰区最大可以直接作为遗传算法搜索的适应度函数，不需转换。如果用盲区最小还要经过一次转换才可作为适应度函数。

适应度函数计算过程如下：

(1)确定搜索速度范围与主杂波宽度；

(2)计算每个PRI下全部速度范围所在频率门；

(3)按照要求的M/N准则，判断某一速度是否位于速度清晰区；

(4)计算所有速度范围落入清晰区的总数。

经过上面四个步骤所得结果就为适应度函数。

1.4选择运算

选择运算是从当前代群体中选择出一些比较优良的个体，并按某种规则或模型遗传到下一代群体中，一般要求适应度较高的个体有更多的机会遗传到下一代群体中。本文采用的是比例选择算子，也称为赌盘选择。比例运算执行的过程如下：

(1)计算出群体中所有个体的适应度总和；

(2)计算每个个体的相对适应度大小，即各个个体被遗传到下一代群体中的概率；

(3)使用模拟赌盘[8]操作确定个体被选中的次数。

1.5交叉运算

交叉运算是产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体。本文采用的是单点交叉的方法，其执行的过程如下：

(1)对群体中的个体进行两两随机配对；

(2)对每一相互配对的个体，随机设置某一基因之后的位置为交叉点；

(3)对每一对相互配对的个体，依设定的交叉概率pc在其交叉点处相互交换两个个体的部分染色体，从而产生出两个新的个体。

1.6变异运算

变异运算是将个体的某一个或某一些基因按一个较小的概率进行改变，它也是产生新个体的一种方法。

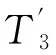
1.7最终结果的选取

经遗传搜索后可以得到很多结果，为了确定这么多结果中哪个或哪几个是最优的，还要进行进一步的筛选。筛选过程如下：

(1) 将最后一代种群中所有个体按适应度大小排序，即按照速度清晰区大小排序；

(2) 选出速度清晰区最大的所有个体；

(3) 计算(2)中选出的所有个体的距离清晰区；

(4) 将个体按距离清晰区从大到小排序，选择距离清晰区最大的个体。

经过上面的四个过程，最终得到的个体速度清晰区最大，同时，距离清晰区也是最大的。最终得到的结果可能不是一个，再结合工程的具体要求加以判断就可以选择出合适的PRI组合。

2　仿真结果

2.1仿真结果

假设载机的飞行速度v0为800 km/h，雷达发射频率f0为3 GHz，占空比为0.1，检测准则为2/4。假设要求雷达的重复频率范围为8 kHz～12 kHz,进行PD处理时的FFT脉冲数为64个，则每个频率门宽度为125.0Hz～187.5Hz。若最小可检测目标速度vmin为40 m/s，则其对应的多普勒频率fmin为800 Hz，对应的多普勒频率门为6.40～4.27，取以0号频率门为中心的共七个多普勒频率门为扣除的频率门，则利用遗传算法得到的一组PRI搜索结果为：[84.0 μs、95.4 μs、106.4 μs、124.4 μs]。其对应的距离盲区见图2，速度盲区见图3，距离-速度二维盲区见图4。仿真时种群中个体数目为500个，交叉概率Pc=0.6，变异概率Pm=0.01，进化数为30代。

图3　速度盲区图

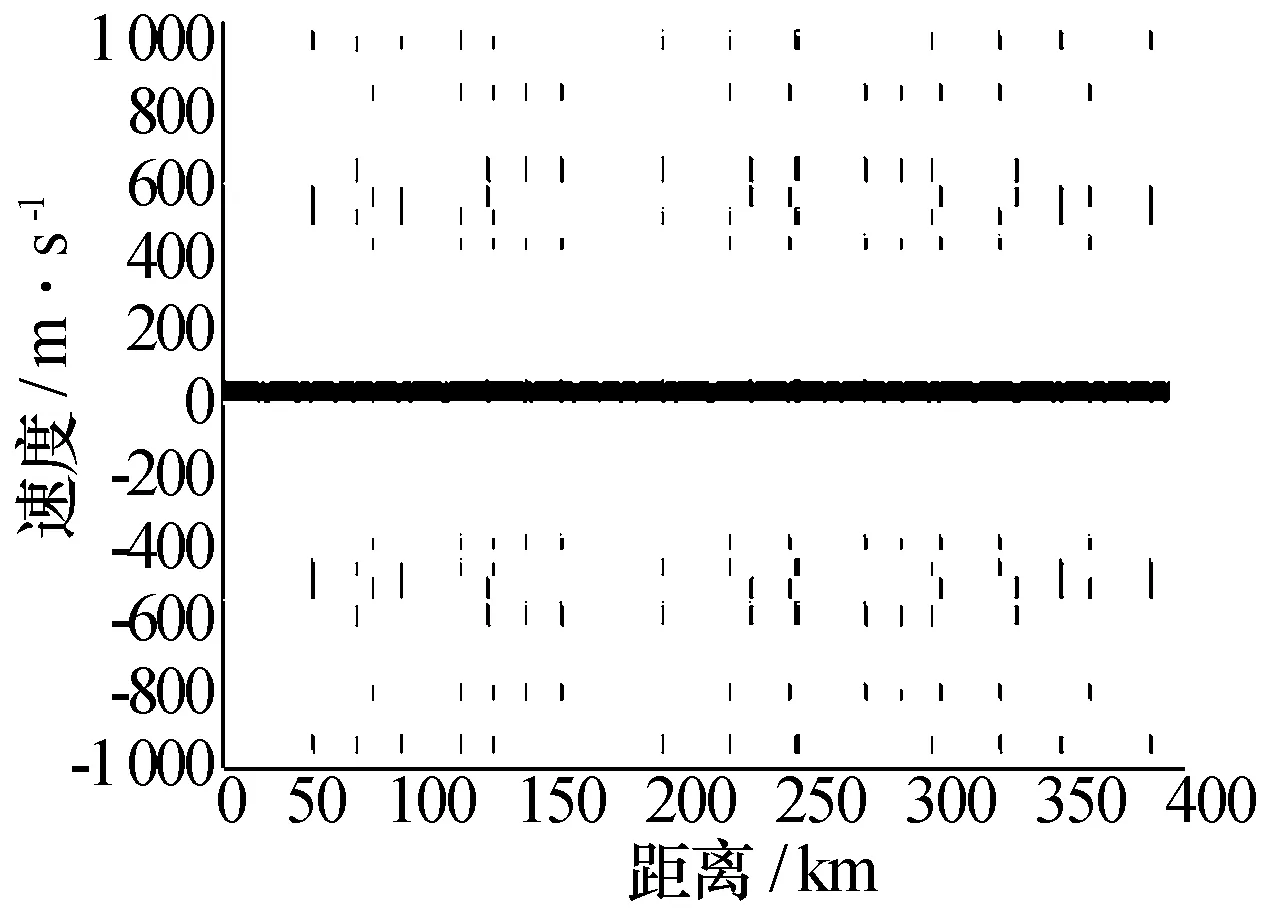
图4　距离-速度二维盲区图

可以看出：遗传算法搜索结果在单独的距离或速度上均可以满足至少两帧清晰的要求，达到工程要求。

2.2计算量分析

3　结束语

遗传算法是一种高效的次最优搜索算法，可有效解决工程优化问题，其最重要的就是适应度评价函数的设计。机载雷达探测目标时，探测到的目标多普勒速度在一段时间内几乎是不变的。如果此时正好落在速度盲区，会导致目标无法检测。而目标的距离始终都在快速变化，即使在某些距离区上存在一定的盲区，经很短时间即可跨越盲区，对目标检测影响不大。本文正是针对机载雷达的这一特点，设计了适应度评价函数。仿真表明：本文采用的方法可以快速、有效搜索出满足机载雷达探测要求的PRI组合。

[1]贲德．机载脉冲多普勒雷达[M]． 北京: 电子工业出版社， 2006．

BEN De．Airborne pulse Doppler radar[M]． Beijing: Publishing House of Electronics Industry，2006．

[2]郦能敬. 预警机系统导论[M]. 北京: 国防工业出版社, 1998.

LI Nengjing. Introduction of airborne early warning system[M]. Beijing: National Defense Industry Press, 1998.

[3]SKOLNIK M I．Radar Handbook[M]．2nd ed. NewYork： McGraw-Hill，1990.

[4]田黎育, 高梅国. 距离-速度二维波形分析跟踪[J]. 现代雷达, 2002, 24(6): 39-42.

TIAN liyu，GAO meiguo. A method for digital moving target tracking based on distance-speed two dimensions waveform analysis[J]. Modern Radar, 2002, 24(6)：39-42.

[5]周明，孙树栋． 遗传算法原理及应用[M]． 北京: 国防工业出版社， 2000．

ZHOU Ming，SUN Shudong．Genetic algorithms: theory and applicaitons [M]．Beijing: National Defense Industry Press，2000．

[6]GAAFAR L K, MASOUD S A. Genetic algorithms and simulated annealing for scheduling in agile manufacturing[J]. International Journal of Production Research, 2005, 43(14): 189-216.

[7]HOLLAND J H. Adaptation in natural and artificial systems[M]. Cambridge, MA: MIT Press, 1975.

[8]GOLDBERG D E. Genetic algorithms in search, optimization and machine learning, reading[M]. MA: Addison-Wesley, 1989.

华瑶女，1965年，高级工程师。研究方向为机载火控雷达系统技术。

Pulse Repetition Interval of Searching Radar under Genetic Algorithm

HUA Yao，SUN Xiaowen

(Nanjing Research Institute of Electronics Technology, Nangjing 210039, China)

Radars referred to as pulse-Doppler are systems that transmit several pulse trains of different pulse repetition interval(PRI) for target detection. The brute force is one of the conventional methods for the selection ofPRIin engineering, and it is computationally intensive. Aiming to characteristic of the target in the air, the genetic algorithm (GA) based on the fitness evaluation function which combines the blind velocity and blind range is presented to improve the efficiency ofPRIsearch in the paper. Simulation results demonstrate the perfect performance of the proposed method and the detailed analysis of computationally cost based on GA method is made. Compared with the brute force, the GA method reduces the computation cost evidently and is suited for the rapid optimal search of radarPRIcombination in engineering, and the results show the method's engineering applicability.

genetic algorithm; pulse repetition interval; blind zone

10.16592/ j.cnki.1004-7859.2016.08.004

华瑶Email：njsss102@163.com

2016-04-29

2016-07-01

TN957.51

A

1004-7859(2016)08-0017-03