考虑不同配筋率影响的板柱节点抗冲切性能分析①
陈建伟,边瑾靓,王 宁,苏幼坡
(1.华北理工大学 建筑工程学院,河北 唐山 063009; 2.河北省地震工程研究中心,河北 唐山 063009)
考虑不同配筋率影响的板柱节点抗冲切性能分析①
陈建伟1,2,边瑾靓1,王宁1,苏幼坡1,2
(1.华北理工大学 建筑工程学院,河北 唐山 063009; 2.河北省地震工程研究中心,河北 唐山 063009)
冲切破坏是钢筋混凝土板柱结构的主要破坏形式。通过对ACI318-08、Eurocode 2、GB50010-2010等规范中关于板柱节点受冲切承载力计算公式的对比分析,发现对于板中配筋率的影响可否忽略以及影响程度等问题的考虑并不统一。为深入研究配筋率对板柱节点抗冲切性能的影响,在考虑材料和几何非线性的基础上,通过有限元软件OpenSEES对5个配筋率分别为0.5%(2个)、0.99%、2.0%及3.0%的板柱节点试件进行数值模拟和参数分析,对比分析各试件的承载力、刚度变化过程及破坏特征,发现模拟结果和试验结果吻合较好。研究表明:配筋率是进行板柱节点抗冲切设计不可忽略的影响因素,建议在规范修订中考虑此参数。最后还分析了其抗震性能及混凝土强度对抗冲切承载力的影响。
板柱结构; 配筋率; 抗冲切性能; OpenSEES
0 引言
板柱结构是建筑结构中常用的形式之一,它可将荷载由楼板直接传递到柱上,而不需要设置主梁和次梁,因此被广泛应用于工业厂房、商场、车库、办公楼及住宅等建筑[1-2]。由于其具有结构简单、降低层高等特点,在国外高层公寓的建设中得到快速发展。通常板上的均布荷载均较小,在正常配筋下板的抗弯能力均可保证,但当板柱节点要承受板传来的较大集中力作用时,节点抗冲切强度通常难以保证。因此板柱结构中,节点冲切破坏形式起到控制作用成为这种结构体系设计中的关键问题之一。
国内外对钢筋混凝土板柱节点抗冲切承载力计算理论的研究成果颇多,运用各种理论与方法(如屈服线理论、刚塑性理论、极限平衡理论等)对钢筋混凝土板的受冲切承载力问题进行了研究,但总的来说,由于节点受力的复杂性,理论上并没有得到统一,尤其体现在各国规范中对于冲切承载力的计算基本属于经验公式,缺乏有力的理论支持。Zineddin等[3]研究了不同配筋以及不同冲击能量的板的动力反应和钢筋混凝土板的抗冲击性能,发现配筋率与冲击高度极大地影响了板的破坏模式。Stefano等[4]对11个低配筋率的板柱节点进行了试验分析,并通过3组1/2缩尺、全尺寸、双倍尺寸试验模型研究了节点抗冲切性能中的尺寸效应。在美国ACI318-08、欧洲Eurocode 2、我国GB50010-2010等规范中发现对于板中配筋率的影响可否忽略以及影响程度等问题的考虑并不统一。因此,为深入研究配筋率对板柱节点抗冲切性能以及破坏特征的影响,对5个配筋率分别为0.5%(2个试件)、0.99%、2.0%及3.0%的板柱节点抗冲切性能以及破坏特征进行数值模拟和参数分析,对比分析各试件的承载力、刚度变化过程及破坏特征。
1 相关规范对比分析
1.1Eurocode 2中抗冲切强度的计算
欧洲混凝土设计规范Eurocode 2[5]中提出的板抗冲切强度计算公式为:
(1)
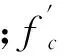

(2)

1.2ACI318-08中抗冲切强度的计算


(3)
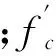

图1 配筋率对板冲切强度影响示意图Fig.1 The effect of reinforcement ratio on punching strength of slabs
由式(3)可知,该计算方法忽略了配筋率对冲切强度的影响,再根据图1可以看出,在配筋率较大的情况下,采用该方法会略低估冲切强度。
1.3GB50010-2010中抗冲切强度的计算
自上世纪八十年代以来,我国进行了大量的自主性板柱构件试验,在此基础上,混凝土设计规范几经修订。最新规范GB50010-2010中规定[7],在局部荷载或集中反力作用下不配置箍筋或弯起钢筋的板,其受冲切承载力应符合下列规定:
Fl≤0.7βhftηumh0
(4)
式中:βh为截面高度影响系数;ft为混凝土轴心抗拉强度设计值;η为系数,可由GB50010-2010规范公式确定;um为计算截面周长;h0为截面的有效高度。
我国在TJ10-74规范制定之前,对于冲切方面的试验研究基本上是空白的,且74规范主要借鉴前苏联的混凝土设计规范,后在此基础上逐步进行修订。从式(4)可以看出,该公式也没有考虑配筋率对冲切承载力的影响。
综上所述,各国混凝土设计规范中,计算冲切强度时考虑配筋率的影响并不统一,ACI318-08和GB50010-2010中都没有考虑配筋率的影响。从图1可以看出,对于低配筋率板的破坏形式主要是冲切破坏,根据ACI318-08所确定的冲切强度或多或少地保守于由Eurocode 2所确定的冲切强度,并且随着板厚的增加,这种低估程度会增加,而ACI318-08所确定的冲切强度又会高估冲切强度。在高配筋率的情况下,根据ACI318-08所确定的冲切强度较为保守。因此,考虑配筋率对冲切强度的影响就显得尤为必要。深入研究不同配筋率对冲切强度计算的影响及影响程度,可为我国混凝土强度设计规范修订提供必要的理论参考依据。
2 试件及试验简介
Elstner等[8]进行了大量的试验研究,尤其是考察了配筋率、柱尺寸、边界约束等因素对钢筋混凝土板抗冲切性能的影响,其试件与配筋如图2、3所示。

图2 加载试验装置Fig.2 Testing arrangement

图3 板柱结构节点配筋图Fig.3 Reinforcement drawing of slab-column connections
为考察不同配筋率对板柱节点抗冲切性能的影响,在试验第Ⅷ系列中选择五个试件进行研究,其中部分试件的混凝土设计强度、板有效高度、柱横截面的尺寸及边界约束条件等基本参数均相同。该组试件能够准确反映配筋率对力学性能的影响。
选取5个板柱节点试件,均采用上下双层配筋(图3),板的厚度均为152.4 mm,但配筋率不同,其基本参数如表1所列。试件放置在一个914 mm高的混凝土框架上,有利于观测到受拉表面裂缝的出现过程及形式。如图2所示的试验装置,在试件与混凝土试验装置的接触部位加50.8 mm×25.4 mm的木垫块,然后通过图2所示的柱头施加竖向荷载。

表1 板柱结构试件的基本参数
3 数值分析模型
3.1OpenSEES计算平台
OpeSEES是以“太平洋地震工程研究中心”为主导,由加州大学伯克利分校开发的非线性有限元计算平台[9-10]。OpenSEES 主要用于土木工程和岩土工程领域结构的地震性能模拟,具有易于改进和开发的优点,能够使用最新的材料模型、单元模型、分析方法等模型参数。其在国内正在逐步引起结构工程领域相关人员的关注和重视。
3.2三维网格梁模型的建立
3.2.1三维网格梁有限元模型
国内外对板柱结构进行数值分析的研究成果已经很多,比如采用极限平衡法、刚塑性理论、等代框架法等方法[11]。Coronelli[12]、Ying[13]和陈建伟[14-15]等提出的网格梁模型是在Yettram等[16]的基础上提出的,即将板柱结构用一些横向和纵向相互垂直的网格梁来代替,交点即为网格梁的节点。本文对Coronelli提出的网格梁模型进行如下的改进和约定:选取网格梁的长度为柱截面尺寸或整数分之一,保证梁与柱连接处的梁单元个数不少于两个。经过模拟分析证明,通过以上选取后,模拟结果的精度和稳定性均有显著提高。另外,经计算钢筋与混凝土之间的粘结滑移对柱冲切承载力影响并不显著,故文中未考虑此参数。
3.2.2节点与单元设置
板柱节点试件尺寸如图4所示。以柱截面尺寸为网格梁长度建立模型,其节点设置如图5所示。
模型共划分了64个节点,OpenSEES中节点命令为“node *”。试验荷载施加在柱上,图5中304、305、404和405节点采用equalDOF命令,保证加载与试验一致。为保证约束条件和试验一致,在节点4、5、301、401、704、705、308和408上施加约束,约束试件平动能力,不约束其转动能力。

图4 试件尺寸(单位:mm)Fig.4 Specimen size (Unit:mm)

图5 节点设置Fig.5 Node setting
模型以横向(图5中X方向)和纵向(图5总Y方向)划分单元,即形成了横向和纵向相互垂直的网格梁单元,文中统一为“网格梁模型”。单元命令采用“element nonlinearBeamColumn *”,单元的积分点个数为5。
3.2.3截面与材料本构
由于采用柱截面尺寸为网格梁长度建立模型,所以网格梁的截面长度和高度分别为柱截面尺寸和板的厚度。划分出来的梁单元截面分成内部单元截面尺寸为254 mm×152.4 mm和边缘单元截面尺寸为152.4 mm×152.4 mm两种,即内节点与外节点所对应的单元截面是不同的,如图6所示。本文单元梁截面先分别定义Steel01钢筋本构模型、Elastic弹性本构模型和Hysteretic模型[17],再采用Section Agrregator将3种材料本构模型进行聚合定义。其中Steel01钢筋本构模型与Hysteretic模型的本构关系如图7(a)和(b)所示。Elastic弹性本构模型是不考虑材料屈服段的完全弹性应力应变曲线。

图6 内外节点示意图Fig.6 Diagram of internal and external nodes

图7 本构关系Fig.7 Constitutive relation
图7(a)中b为刚度衰减系数,E0为初始弹性模量,bE0是钢筋屈服后衰减的弹性模量,fy为受拉钢筋屈服强度。
3.2.4模型计算
积分类型定义为Displacement Control,迭代计算采用Newton,选用能量准则为收敛准则,自由度数目控制选项设为Plain。
4 数值与试验结果对比分析
4.1数值分析结果
基于三维网格梁有限元分析模型,对表1中的5个代表性试件按照改进模型的建议和方法分别进行建模计算,数值分析结果与试验结果的对比如图8所示。

图8 试件的荷载位移曲线Fig.8 Load-displacement curves of specimens
图8中,最大荷载值除B14的误差超过了10%外,其余均小于10%,这表明三维网格梁模型模拟结果与试验结果吻合较好。
4.2配筋率影响分析
5组试件中,混凝土设计强度均为44.8 MPa,而B2、B4、B9及B14的主要区别是板的配筋率分别为0.5%、0.99%、2%及3%。将5组试件进行对比分析,以探究配筋率对板抗冲切性能的影响,结果如图9所示。
由图9可以看出,试件B14的最大荷载约为试件B2的3.13倍,且试件配筋率越高,试件的延性相对降低,配筋率对于板冲切承载力的影响是十分显著的。表2将4组试件的最大荷载进行归纳并给出与中国混凝土结构设计规范(GB 50010-2010)、美国规范(ACI 318-08)、欧洲规范(EC 4)所计算出的抗冲切承载力进行对比分析。

图9 配筋率对比分析Fig.9 Comparative analysis of reinforcement ratio
表2对比分析发现,由于中国规范中没有考虑配筋率对板冲切性能的影响,所得到的抗冲切承载力较模拟所得到的最大荷载,其离散性较大。

表2 模拟和规范计算值与试验值对比分析
4.3混凝土影响分析
试件B1和B2的配筋率均为0.5%,混凝土设计强度分别为13.8 MPa和44.8 MPa。对2组试件进行对比,观察混凝土强度对于板抗冲切性能的影响,结果如图10所示。

图10 混凝土强度对比分析Fig.10 Comparative analysis of concrete strength
由图10可以看出,试件B2的最大荷载约为B1的1.01倍,基本相等。混凝土强度对于试件加载初期影响较为显著,但对于板最大冲切承载力值影响不大。
通过对配筋率和混凝土强度对比可以发现,混凝土强度对于板最大冲切承载力的影响并不大,而配筋率的影响显著,我国规范在规定抗冲切承载力设计值时应该考虑配筋率对板抗冲切性能的影响。
5 变形分布与屈服节点模拟
5.1变形分布模拟
国内外试验研究中,通过数值分析模型对节点变形分布进行很好模拟的并不多见。文中网格梁模型与试验结果吻合较好,运用OpenSEE有限元软件对试件的节点变形分布进行模拟。在网格梁模型中取一条直线1,直线通过201~208节点,观察8个节点的变形分布,如图11所示。对5组试件进行变形分布模拟,如图12所示,其中试件B1、B2及B4选取柱变形yc分别是5.08 mm、10.16 mm及15.24 mm时直线1上各节点变形情况,B9和B14选取柱变形yc分别是2.54 mm、5.08 mm、7.62 mm时直线1上各节点变形情况。

图11 变形模拟的节点选取Fig.11 Node selection of deformation simulation
由图12可知,当中柱变形均为5.08 mm时,5组试件的各节点变形分布基本相似。高配筋率试件(B9、B14)的中柱变形与试件B1、B2、B4的差值与各节点变形差值也基本相似,说明配筋率对于板各节点的变形发展模式影响不大。
5.2屈服节点模拟
网格梁模型也可以对试件的屈服节点进行模拟,模拟以单元为单位,圆点表示此单元内相应节点产生屈服。模拟发现试件B1、B2、B4的屈服节点相同,如图13(a)所示。图13(b)为试件B9屈服节点图,试件B14未发生屈服。

图12 试件变形分布Fig.12 Deformation distribution of specimens

图13 试件屈服节点模拟Fig.13 Yield node simulation of specimens
通过模拟发现板柱结构的屈服总是先发生在板柱交界处,然后由交界处向外传播。试件B9屈服节点并未向外传播,但图13(a)所示3个试件的屈服节点都由交界处向外传播,虚线所表示的屈服线与Elstner[8]所列出屈服线模式相吻合。
6 抗震性能模拟
2008年Ying等[18]对不同形式荷载下的板柱节点进行了试验研究,包含配筋率对板柱节点抗震性能影响,认为配筋率的提高将显著提高板柱节点的侧向刚度。在文中模型与试验模拟吻合较好的基础上,对试件进行抗震性能研究,验证侧向刚度是否会显著提高。选取混凝土强度相同、配筋率分别为0.99%和3%的B4和B14试件,将两个构件都填加长度为10 mm且刚度无限大的柱头,在柱头上分别施加步长2.5、5和10 mm的水平往复荷载,得到滞回曲线如图14所示。不同步长对应的最大水平荷载如表3所示。从表3中可以看出,B14的侧向刚度显著大于B4,即配筋率的提高显著提高了板柱节点的侧向刚度。

图14 试件的滞回曲线Fig.14 Hysteretic curves of specimens

工况最大水平荷载/kN2.5mm5mm10mmB4(0.99%)B14(3.00%)141.9319.4155.7373.7174.6447.4
《建筑抗震试验方法规程》规定采用等效黏滞阻尼系数来衡量抗震试验中试件耗能能力的大小,系数越大则耗能能力越好,阻尼系数的计算公式如式(5)所示,示意图如图15所示。取B4及B14一个步长的滞回曲线,运用式(5)对其进行计算,得到B4的阻尼系数he=0.4,B14的he=0.35,配筋率较小的B4所得等效黏滞阻尼系数略大。
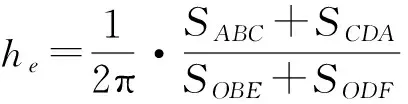
(5)

图15 耗能能力计算示意图Fig.15 Diagram of energy dissipation capacity calculation
7 结论
(1)通过OpenSEES建模分析表明模拟结果与试验结果吻合较好,说明了网格梁模型对板柱结构模拟的合理性。文中所采用的节点、单元、截面的划分以及材料本构的定义较为合理,网格梁模型可以参照其建立。
(2)板柱节点随着配筋率的提高,其侧向刚度将显著提高。
(3)配筋率对于板承载力和延性均有影响,配筋率越大,板的延性相对降低,其最大冲切承载力值增加,但配筋率对于板各节点的变形发展模式影响不大。
(4)混凝土强度对板最大抗冲切承载力值影响不大,配筋率是进行板柱节点抗冲切设计不可忽略的影响因素,欧洲规范考虑了配筋率对抗冲切承载力的影响,建议我国在规范修订中也应充分考虑此点。
References)
[1]Luo Y H,Durrani A J,Conte J P.Equivalent Frame Analysis of Flat Plate Buildings for Seismic Loading[J].Journal of Structural Engineering ASCE,1994,120(7):2137-2155.
[2]Robertson I N.Analysis of Flat Slab Structures Subjected to Combined Lateral and Gravity Loads[J].ACI Structural Journal,1997,94(6):723-729.
[3]Zineddin M,Krauthammer T.Dynamic Response and Behavior of Reinforced Concrete Slabs under Impact Loading[J].International Journal of Impact Engineering,2007,106(1):1517-1534.
[4]Guandalini Stefano,Burdet Olivier,Muttoni Aurelio.Punching Tests of Slabs with Low Reinforcement Ratios[J].ACI Structural Journal,2009,34(9):87-95.
[5]CEN,Eurocode 2-Design of Concrete Structures:Part 1-1 General Rules and Rules for Buildings[S].2004.
[6]ACI Committee 318,Building Code Requirements for Structural Concrete (ACI-318)and Commentary[S].2005.
[7]GB50010-2010,混凝土结构设计规范[S].北京:中国建筑工业出版社,2011.
GB50010-2010,Code for Design of Concrete Structures[S].Beijing:China Architecture & Building Press,2011.(in Chinese)[8]Elstner R C,Hognestad E.Shearing Strength of Reinforced Concrete Slabs[J].ACI Journal Proceedings,1956,53(1):29-58.[9]郑山锁,王唯,李龙,等.基于纤维模型的型钢混凝土柱精细化建模分析[J].广西大学学报:自然科学版,2012,37(2):197-203.ZHENG Shan-suo,WANG Wei,LI Long,et al.Accurate Modeling of SRC Columns Based on OpenSees[J].Journal of Guangxi University:Nat Sci Ed,2012,37(2):197-203.(in Chinese)
[10]OpenSees Command Language Manual.Open System for Earthquake Engineering Simulation[DB/OL].2010,http:// opensees.berkeley.edu.
[11]刘立渠,黄小坤,陶学康.考虑纵筋率及加载面边长比影响的板受冲切承载力计算分析[J].土木工程学报,2008,41(7):27-32.
LIU Li-qu,HUANG Xiao-kun,TAO Xue-kang.Analytical Study on the Punching Shear Capacity of Slabs Considering the Influences of Tension Reinforcement and Column Aspect Ratios[J].China Civil Engineering Journal,2008,41(7):27-32.(in Chinese)
[12]Coronelli D.Grid Model for Flat-Slab Structures[J].ACI Structural Journal,2010,107(6):645-653.
[13]Ying Tian,Jianwei Chen,Aly Said,et al.Nonlinear Modeling of Flat-plate Structures Using Grid Beam Elements[J].Computers and Concrete,2012,10(5):491-507.(in Chinese)
[14]陈建伟,苏幼坡,杨梅.板柱节点抗冲切性能分析的力学转化模型[J].力学与实践,2012,34(5):57-60.
CHEN Jian-wei,SU You-po,YANG Mei.Mechanical Transformation Model of Punching Shear Capacity Analysis for Slab-Cloumn Connections[J].Mechanics in Engineering,2012,34(5):57-60.(in Chinese)
[15]陈建伟,苏幼坡,丁峰.不平衡弯矩作用下板柱节点抗冲切性能非线性分析[J].世界地震工程,2012,28(4):75-79
CHEN Jian-wei,SU You-po,DING Feng.Nonlinear Analysis of Punching Shear Resistance Capacity for Slab Column Connections under Unbalanced Moment[J].World Earthquake
Engineering,2012,28(4):75-79.(in Chinese)
[16]Yettram A,Husain H M.Grid-framework Method for Plates in Flexure[J].Eng Mech Div ASCE,1965,63(3):53-64.
[17]Haruki Aakiyama,Neil M Hawkins.Response of Flat Plate Concrete Structures to Seismic and Wind Forces,SM84-1[R].The National Science Foundation Earthquake Hazards Mitigation Program Grant No.ENV 72-03585,University of Washington,Seattle,WA,98195,July,1984.
[18]Ying Tian,James O Jirsa,Oguzhan Bayrak,et al.Behavior of Slab-column Connections of Existing Flat-plate Structures[J].ACI Structural Journal,2008,105 (5):561-569.
[19]郑山锁,代旷宇,孙龙飞,等.钢框架结构的地震损伤研究[J].地震工程学报,2015,37(2):290-297
ZHENG Shan-suo,DAI Kuang-yu,SUN Long-fei,et al.Research on the Seismic Damage of Steel Frame Structure[J].China Earthquke Engineering Journal,2015,37(2):290-297.
Punching Shear Capacity Analysis of a Slab-column Connection Considering the Effect of Different Reinforcement Ratios
CHEN Jian-wei1,2,BIAN Jin-liang1,WANG Ning1,SU You-po1,2
(1.College of Civil and Architectural Engineering,North China University of Science and Technology,Tangshan 063009,Hebei,China;2.Earthquake Engineering Research Center of Hebei Province,Tangshan 063009,Hebei,China)
A slab-column structure is a bearing system,which is composed of a plate and a column.Because there are no ribs,force transfer is simple,that is to say,the load passes to the foundation directly through the column.This structure has some advantages such as optimization of space and steel plate use,layout flexibility,and quick construction.To improve the punching shear capacity of the concrete slab and to reduce its span,we often set the column head on top of the column.Punching shear has been the object of intense experimental effort since the 1950s.Some codes account for size or membrane effects,or the ratio of column size to the depth of the slab.Here,comparative analysis of formulas for punching shear strength calculations following ACI318-08,Eurocode 2,and GB50010-2010 is carried out.The research shows that the effect of the reinforcement ratio is not always uniform.Using five samples with different reinforcement ratios,which is 0.5% (two),0.99%,2.0%,and 3.0%,respectively,the numerical simulation and parameter analysis is performed with Open System for Earthquake Engineering Simulation (OpenSEES)considering the material nonlinearity and geometric nonlinearity.The proposed numerical method successfully simulates the punching shear capacity of slab-column connections in terms of the load-deformation curve,stiffness variation,and failure characteristics.The research results show that the reinforcement ratio is the key factor in punching shear resistance and should be considered appropriately in any code revision.Finally,the analysis of punching shear strength is also presented with regard to concrete.
slab-column structure; reinforcement ratio; punching shear capacity; OpenSEES
2015-07-23
国家自然科学基金项目(51278164);河北省重点基础研究项目(14965406D)
陈建伟(1978-),男,副教授,主要从事工程抗震与防灾减灾方面的研究。E-mail:heuu2010@163.com。
TU375.2
A
1000-0844(2016)04-0525-08
10.3969/j.issn.1000-0844.2016.04.0525

