连续降雨条件下某震后高边坡稳定性分析①

邹祖银,朱占元,张　锋,陈婷婷,张自兴

(1.四川农业大学土木工程学院,四川 都江堰 611830;2.村镇建设防灾减灾四川省高等学校工程研究中心,四川 都江堰 611830;3.哈尔滨工业大学交通科学与工程学院,黑龙江 哈尔滨 150090)



连续降雨条件下某震后高边坡稳定性分析①

邹祖银1,2,朱占元1,2,张锋3,陈婷婷1,2,张自兴1,2

(1.四川农业大学土木工程学院,四川 都江堰 611830;2.村镇建设防灾减灾四川省高等学校工程研究中心,四川 都江堰 611830;3.哈尔滨工业大学交通科学与工程学院,黑龙江 哈尔滨 150090)

基于饱和-非饱和渗流理论,综合考虑降雨入渗引起土体重量增加、渗透力增大以及抗剪强度降低等因素的影响,建立降雨条件下震后高边坡有限元模型,运用自编计算程序USLOPE-FEM进行稳定性分析。研究结果表明:未降雨之前,坡体塑性应变主要集中分布于松散堆积体下部与基岩分界面,边坡已经接近临界平衡状态;降雨量20 mm/h时连续入渗使边坡上部土层含水量增加,负压区消失且出现饱和区;随着降雨时间延长,坡体表层暂态饱和区逐渐向内部推移,土体的重量和渗透力显著增大、抗剪强度明显降低,坡体中剪应力整体增大,塑性应变区向坡顶扩展而逐渐贯通;连续降雨6 h后,临空面表层出现局部滑塌,连续降雨36 h后整个堆积层将沿基岩滑塌逐步堵江。研究成果可为强降雨条件下边坡安全性评价提供参考,也为该边坡的失稳预警与滑坡防治积累资料。

边坡工程; 强降雨; 稳定性分析; 饱和-非饱和渗流; 汶川地震

0　引言

震惊中外的“5·12”汶川大地震让数万生命毁于一旦,生态环境也被瞬息改变。大量滑坡、崩塌是改变山河面貌的主要因素,也是导致人员伤亡、财产损失、设施破坏的一个重要原因[1-2]。地震诱发崩塌、滑坡产生的大量松散固体物质还残留在山体上,近几年强降雨诱发再次滑坡崩塌乃至形成泥石流灾害的案例不胜枚举[3-5]。震后高边坡的安全性评价倍受当地政府、民众以及学术界的广泛关注。

连续降雨是诱发边坡失稳的重要因素之一,也是国内外边坡工程的研究热点[1-25]。为了深入探究降雨诱发边坡失稳的机制和规律,A.Tohari等[20-21]陆续进行了降雨入渗模型和原位试验研究;基于Mohr-Coulomb准则和有效应力原理,D.G.Fredlund等[22-23]提出并发展了一些非饱和土强度准则,促进了非饱和土土力学的快速发展;在数值模拟方面,基于饱和-非饱和渗流理论,有研究采用极限平衡法和强度折减有限元法评价降雨入渗条件下的边坡稳定性[17]。然而,强降雨入渗条件下饱和-非饱和边坡失稳原因极其复杂,如何综合考虑多种因素的联合作用,特别是土体质量增加和强度参数软化对边坡稳定性影响的研究还不够深入。

鉴于此,本文针对某汶川地震震后高边坡实际工程,以避免或减轻滑坡灾害为应用背景,基于自编饱和-非饱和降雨入渗程序USLOPE-FEM,进行边坡稳定性分析,以揭示连续降雨震后高边坡失稳机理,为强降雨条件下边坡稳定性分析与安全性评价提供一般的技术思路和经验参考,也为震后高边坡的失稳预警与滑坡防治准备必要的基础资料。

1　工程地质与滑坡概况

1.1滑坡概况

大咀山高边坡系“5·12”汶川地震诱发的滑坡,位于平通镇牛斐村涪江上游(图1),地理坐标为104°39′46″E,32°47′27″N。滑坡体近似于马蹄形,前缘宽456 m,轴线长71 6 m,海拔660～1 300 m,厚度10～60 m,体积超过100×104m3。

震后滑坡的山体,上覆土层为大面积分布厚度较大、松散、易渗水的残留滑坡坡积土,下伏基岩为较密实且相对隔水的板岩,并且由于土层向下蠕动、地表水径流与入渗、地下水渗流与渗出等的长期作用,导致残坡积层中形成较多的土体蠕滑裂缝、地表水径流切沟、地表水入渗侵蚀通道和地下水渗流潜蚀通道等,既破坏了残坡积层的完整性、降低了土体及其与基岩接触面的抗剪强度,又为地表水入渗、地下水渗流创造了有利条件。故此,在强降雨条件下上覆土层容易沿基岩接触面滑塌而形成再次滑坡,如2009年6月下旬的连续暴雨就触发了其局部的再次滑坡。若长时间连续大暴雨,极有可能出现大规模滑坡堵江,因此对其开展强降雨条件下边坡稳定性评价势在必行。

1.2工程地质

据四川省冶金地质勘查局水文工程大队调查资料,滑坡体地形条件易形成滑坡(图1),其后缘坡度约50°～66°,残留滑体堆积集中区约31°～52°,前部坡度约17°～52°。

图1　震后高边坡现场照片Fig.1　Site photos of the high slope after earthquake

基底为志留系茂县群组(SMX23)千枚岩:绿灰色,风化后成黄褐色,隐晶质结构,板状、 千枚状构造,勘察揭露范围内,主要为强中～等风化板岩,局部见全风化板岩。劈理面平直光滑,无填充,产状322°～348°∠50°～66°。岩体主要受两组结构面切割,其产状分别为185°∠54°和234°∠47°,结构面平直光滑,无填充。

1.3气象条件

平通镇牛斐村属北亚热带山地湿润季风气候区,具有冬寒夏热、四季分明、夏秋多雨、冬春干旱等特点。根据平武县与绵阳气象站历年气象资料统计:多年平均降雨量为960.40 mm,最大日降水量186.0 mm,降雨主要集中于7—9月,占全年的75.5%;年平均相对湿度72%;多年平均蒸发量1 074.3 mm,多年平均日照1 323.0 h,多年平均雷雨日28.4天,多年平均霜日数为48.1天。

2　降雨条件下非饱和土边坡稳定性分析模型与计算参数

2.1饱和土-非饱和土渗流控制方程

基于质量守恒原理和非饱和土Darcy定律,各向异性多孔介质的饱和-非饱和渗流控制微分方程[6-7,24]可写为,

(1)

式中:h为压力水头(饱和区为正值，非饱和区为负值);kr为相对渗透系数(0≤kr≤1);kij为饱和渗透系数;Ss为单位贮水系数;C为容水度，C=dθ/dh，θ为体积含水率;β为特征系数(非饱和区为0，饱和区为1);t为时间;S为源汇项。

式(1)的定解条件为：

初始条件：

h(xi,t)|t=0=h0(xi)

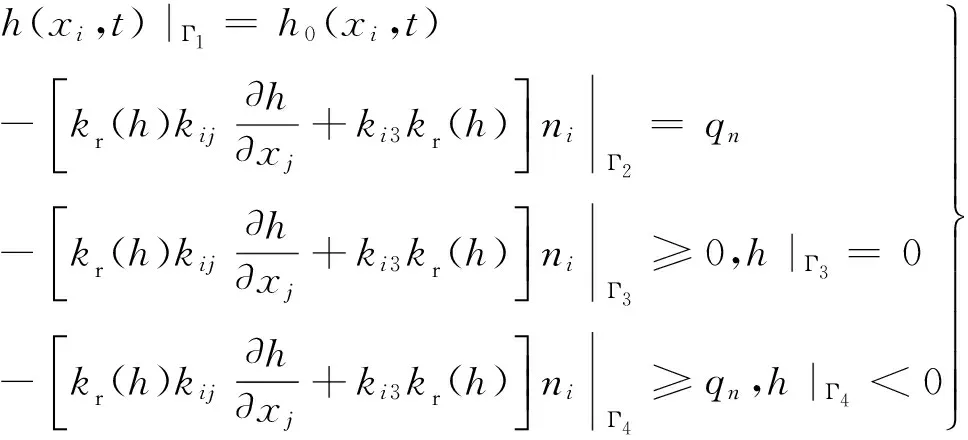
(2)

式中:i=1,2,3;ni为方向余弦;i(t)为入渗率;Γ1为水头边界，Γ2为流量边界，Γ3为饱和逸出边界，Γ4为非饱和逸出边界。对式(2)采用伽辽金加权余量法求解，并在空间上采用有限单元法进行离散，时域上采用隐式向后差分格式进行离散。

2.2降雨入渗边界

降雨条件下，雨水的入渗量与土体的渗透性、干湿度及降雨强度、降雨持时等因素有关。可采用Darcy定律计算垂直地表的最大入渗能力，

(3)

当q(t)≤R(t)时，全部入渗，即R(t)|Γ5=q(t)；当q(t)>R(t)时，坡面形成定水头饱和入渗，即h(xi,t)|Γ1=z(xi)。式中:q(t)为降雨强度Q(t)在入渗面上的分量，q(t)=Q(t)ni，ni为入渗面方向余弦。

2.3水力渗透参数

与饱和土不同，非饱和土的水力渗透参数为压力水头(基质吸力，体积含水量或饱和度)的函数，可由土水特征曲线得出。常用的拟合模型很多，本项目采用Van Genuchten模型[6-7,24](即VG模型)拟合水力渗透参数，

(4)

式中:Se为饱和度;θ=nSe为体积含水量;n为孔隙率;α、β、m分别为模型拟合参数，m=1-β-1。

2.4土的重力增量离散

因降雨持时延长，边坡土体含水量增大，土的重度增加使得下滑力增大。降雨入渗后土的重度为γ=γd+Se(γs-γd)。将由降雨入渗引起的土的附加重力增量等效为节点荷载[7]，

{ΔRg}e=∭[N]T{ΔP}=dxdydz

(5)

式中:{ΔRg}e为降雨入渗附加重力体积力的等效节点荷载;[N]为形函数;{ΔP}为土的重力增量。

2.5渗透力增量离散

基于不同降雨时刻的坡体渗流场，对饱和区根据增量有限元理论计算的由单元渗透体积力增量等效的节点渗透载荷[6]，

{ΔFS}e=-γw∭[N]T{ΔJ}dxdydz

(6)

式中:{ΔFS}e为渗透体积力引起的等效节点荷载;γw为水的容重;[N]为形函数;{ΔJ}为增加的水力梯度。

2.6改进的抗剪强度准则

20世纪60年代以来，国内外很多学者如Bishop等基于Mohr-Coulomb准则提出了非饱和土的强度表达式，其中Fredlund的双参数模型在岩土工程界一度获得广泛认可。本项目基于固结不排水静三轴试验资料，采用土的强度参数与含水量之间的函数关系，考虑含水量对非饱和土强度的影响[6]，

τ=c(θ)+σtanφ(θ)

(7)

式中:τ为总的剪应力;c(θ)为黏聚力与含水量之间的函数关系;φ(θ)为摩擦角与含水量之间的函数关系。该式为总应力强度公式。

此外,根据土的弹-塑性模型和相关联的流动法则,计算因降雨引起的坡体各时段的应力、位移以及塑性应变。基于上述理论,采用Visual Fortran语言编写降雨条件下饱和-非饱和土坡稳定性分析计算程序USlope-Fem,并实现降雨入渗条件下边坡渗流场与瞬态稳定性的数值模拟[7]。

2.7计算参数

平通镇牛斐村大咀山山体高边坡连续降雨条件下稳定性分析的计算模型见图2,横向长930 m,左侧边界高702 m,右侧边界高70 m。基于实际情况,设定:模型左右边界AC、IJ为透水边界,底部AJ为不透水边界,上坡面CDEFGH为降雨入渗边界,坡面HI为饱和逸出边界,GH为非饱和逸出边界。

图2　计算模型(单位:m)Fig.2　Calculation model (Unit:m)

采用等参四边形单元剖分计算域(图3)。左、右竖向边界为水平位移约束,底部水平边界为竖向位移约束,共9 755个节点、9 469个单元。采用弹塑性本构模型,并基于Mohr-Coulomb屈服准则,计算任意时刻坡体内所有节点应力、位移和单元塑性应变。基于现场勘查资料与室内实验结果[25]并参考文献资料,采用Van Genuchten模型(即VG模型)拟合水力渗透参数,渗流场计算参数与应力场计算参数见表1。

图3　计算域单元网格剖分Fig.3　Element meshes in computational domain

表1　物理力学参数

3　计算结果分析

基于勘察资料,设定图2计算模型的右侧、左侧初始水头边界分别为高程710 m、950 m处,假设降雨量20 mm/h,据此对边坡连续降雨入渗条件下饱和-非饱和稳定渗流进行模拟计算。

3.1降雨入渗分析

24小时内坡体内部的水分场变化如图4所示。可以看出,降雨入渗1 h,边坡上部土层含水量增加,负压区消失,出现较浅的饱和区;且因下伏基岩的隔水作用,土层零压面与基岩面之间的水头压力梯度很大,由于下坡面为饱和逸出边界,因而地下水位升高不明显[图4(b)]。随着降雨时间延长,坡体表层便形成暂态饱和区且逐渐向内部推移,由于震后山体破碎,含黏土碎石土层渗透系数很大,入渗速度较快。当降雨24 h后,入渗深度达到10 m以上[图4(c)]。

图4　持续降雨下边坡渗流场变化过程(压力水头,单位:m)Fig.4　Change process of slope seepage field under continuous rainfall (Pressure head,unit:m)

3.2边坡稳定性分析

基于勘察资料与试验结果,及参考文献给出的土的含水量与抗剪强度指标之间关系,确定边坡各土层的弹性模量、抗剪强度指标与含水率之间的函数关系见表1。据此模拟计算边坡连续降雨入渗条件下的应力应变状态并进行安全性评价研究。

降雨初始时刻边坡的最大剪应力云图见图5(a);降雨量20 mm/h、降雨24 h的最大剪应力云图见图5(b)。可以看出,坡体中最大剪应力成层分布,并随深度增加而增大;与降雨前相比,降雨入渗后坡体中最大剪应力整体增大。

图5　最大剪应力(τmax)云图Fig.5　Nephogram of the maximum shear stress τmax

降雨过程中坡体塑性应变变化过程见图6。可以看出,未降雨之前,塑性应变主要集中分布于地震引起的松散堆积体下部土-基岩分界面,边坡已经接近临界平衡状态;降雨入渗后,上部坡体的重量和下部坡体的渗透力均显著增大,致使坡体沿土-基岩分界面的下滑力增加,塑性应变区沿土-基岩分界面向坡顶扩展而逐渐贯通。同时,由于松散堆积体的临空面较陡,当连续降雨6 h后,临空面就会在表层出现局部滑塌,表现为溯源滑动[图6(b)],与图1实际边坡滑动相符,验证了计算结果的正确性;随着降雨的继续进行,滑动面向坡体深入,当连续降雨36 h后,滑动面接近基岩[图6(e)],整个堆积层将沿基岩开始滑塌。

图6　塑性应变(εp)云图Fig.6　Nephogram of plastic strain εp

降雨持续24 h坡体网格位移矢量图见图7。可见,降雨触发坡体位移,特别是边坡上部地震引起的松散堆积体有明显向下滑动的趋势,位移随降雨持续时间的增加而增大。

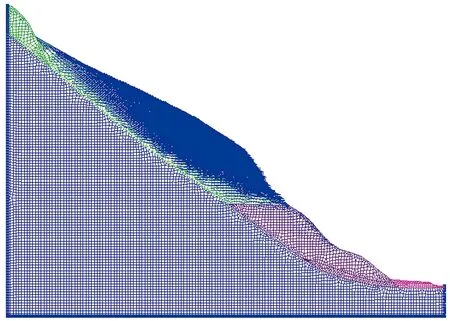
图7　降雨24 h 位移矢量图Fig.7　Vector graph of displacement after rainfall for 24 h

基于强度折减法计算边坡松散堆积体整体安全系数随降雨持续时间的变化关系(图8)。可见降雨持续36 h,其整体安全系数为1.001,处于临界平衡状态;继续降雨将整体下滑、堵江并摧毁对岸公路边的民房,阻断省道S205,形成坝体高度约25 m的堰塞湖,威胁上下游村庄安全。

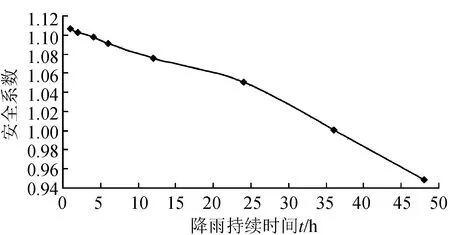
图8　边坡安全系数变化过程Fig.8　Change process of slope safety factor

4　结论

(1)边坡系震后高边坡,“5·12”汶川大地震使山体松动滑塌形成大量残留滑体。未降雨之前,坡体塑性应变主要集中分布于地震引起的松散堆积体下部与基岩分界面,边坡已经接近临界平衡状态。

(2)降雨量20 mm/h,连续入渗使边坡上部土层含水量增加,负压区消失(基质吸力降低)且出现饱和区,土层零压面与基岩面之间的水头压力梯度很大;随着降雨时间延长,坡体表层形成暂态饱和区且逐渐向内部推移,土体的重量和渗透力显著增大、抗剪强度明显降低,坡体中剪应力整体增大且沿土-基岩分界面的下滑力明显增加,塑性应变区向坡顶扩展而逐渐贯通;当连续降雨6 h后,临空面就会在表层出现局部滑塌,表现为溯源滑动;当连续降雨36 h后,整个堆积层将沿基岩滑塌堵江。

(3)建议针对本边坡必须进行预处理或加强变形监测,特别是加强连续降雨时的预警。

References)

[1]殷跃平.汶川地震地质与滑坡灾害概论[M].北京:地质出版社,2009.

YIN Yue-ping.Great Wenchuan Earthquake:Seismogeology and Landslide Hazards[M].Beijing:Geological Press,2009.(in Chinese)

[2]黄润秋,许强.中国典型灾难性滑坡[M].北京:科学出版社,2008.

HUANG Run-qiu,XU Qiang.Catastrophic Llandslides in China[M].Beijing:Science Press,2008.(in Chinese)

[3]崔鹏,韦方强,陈晓清,等.汶川地震次生山地灾害及其减灾对策[J].中国科学院院刊,2008,23(4):317-323.

CUI Peng,WEI Fang-qiang,CHEN Xiao-qing,et al.Geo-hazards in Wenchuan Earthquake Area and Countermeasures for Disaster Reduction[J].Bulletin of Chinese Academy of Sciences,2008,23(4):317-323.(in Chinese)

[4]顾成壮,胡卸文,张茂淳,等.强降雨下饱和平滑型滑坡坡体水流运动及其边坡稳定效应分析——以四川汉源二蛮山滑坡为例[J].岩土力学,2013,34(4):1075-1081.

GU Cheng-zhuang,HU Xie-wen,ZHANG Mao-chun,et al.Analysis of Flow Motion and Its Effect on the Slope Stability of Plane Sliding Landslide Saturated under Heavy-rain——A Case Study of Ermanshan Landslide in Hanyuan County of Sichuan Province[J].Rock and Soil Mechanics,2013,34(4):1075-1081.(in Chinese)

[5]殷志强,徐永强,赵无忌.四川都江堰三溪村“7·10”高位山体滑坡研究[J].工程地质学报,2014,22(2):309-318.

YIN Zhi-qiang,XU Yong-qiang,ZHAO Wu-ji.Sanxi Village Landslide in Dujiangyan,Sichuan Province on July 10,2013[J].Journal of Engineering Geology,2014,22(2):309-318.(in Chinese)

[6]吴李泉,张锋,凌贤长,等.强降雨条件下浙江武义平头村山体高边坡稳定性分析[J].岩石力学与工程学报,2009,28(6):1193-1199.WU Li-quan,ZHANG Feng,LING Xian-zhang,et al.Stability Analysis of High Slope Subjected to Heavy Rainfall in Pingtou Village of Wuyi County,Zhejiang Province[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(6):1193-1199.(in Chinese)[7]ZHU Zhan-yuan,ZHANG Feng,LING Xian-zhang.Rainfall-induce Seepage Field of a High Slope and Its Effect Factors[J].Advanced Materials Research,2011,243-249(1):2423-2428.

[8]许建聪,尚岳全.降雨作用下碎石土滑坡解体变形破坏机制研究[J].岩土力学,2008,29(1):109-113.

XU Jian-cong,SHANG Yue-quan.Study on Mechanism of Disintegration Deformation and Failure of Debris Landslide under Rainfall[J].Rock and Soil Mechanics,2008,29(1):109-113.(in Chinese)

[9]魏宁,茜平一,傅旭东.降雨和蒸发对土质边坡稳定性的影响[J].岩土力学,2006,27(5):778-782.

WEI Ning,QIAN Ping-yi,FU Xu-dong.Effects of Rainfall Infiltration and Evaporation on Soil Slope Stability[J].Rock and Soil Mechanics,2006,27(5):778-782.(in Chinese)

[10]Cai F,Ugai K.Numerical Analysis of Rainfall Effects on Slope Stability[J].International Journal of Geomechanics,2004,4(2):69-78.

[11]Kima J,Jeong S,Park S,et al.Influence of Rainfall-induced Wetting on the Stability of Slopes in Weathered Soils[J].Engineering Geology,2004,75(3/4):251-262.

[12]Cho S E,Lee S R.Evaluation of Surgical Stability for Homogeneous Slopes Considering Rainfall Characteristics[J].Journal of Geotechnical and Geoenvironmental Engineering,2002,128(9):756-763.

[13]Schmertmann J H.Estimating Slope Stability Reduction due to Rain Infiltration Mounding[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(9):1219-1228.

[14]Chen H,Lee C F ,Law K T.Causative Mechanisms of Rainfall-induced Fill Slope Failures[J].Journal of Geotechnical and Geoenvironmental Engineering,2004,130(6):593-602.

[15]Zhan T L T,Ng C W W.Analytical Analysis of Rainfall Infiltration Mechanism in Unsaturated Soils[J].International Journal of Geomechanics,2004,4(4):273-284.

[16]Gavin K,Xue J F.A Simple Method to Analyze Infiltration into Unsaturated Soil Slopes[J].Computers and Geotechnics,2008,35(2):223-230.

[17]李兆平,张弥.考虑降雨入渗影响的非饱和土边坡瞬态安全系数研究[J].土木工程学报,2001,34(5):57-61.

LI Zhao-ping,ZHANG Mi.Effects of Rain Infiltration on Transient Safety of Unsaturated Soil Slope[J].China Civil Engineering Journal,2001,34(5):57-61.(in Chinese)

[18]黄茂松,贾苍琴.考虑非饱和非稳定渗流的土坡稳定分析[J].岩土工程学报,2006,28(2):202-206.

HUANG Mao-song,JIA Cang-qin.Stability Analysis of Soil Slopes Subjected to Unsaturated Transient Seepage[J].Chinese Journal of Geotechnical Engineering,2006,28(2):202-206.(in Chinese)

[19]徐晗,朱以文,蔡元奇,等.降雨入渗条件下非饱和土边坡稳定分析[J].岩土力学,2005,26(12):1957-1962.

XU Han,ZHU Yi-wen,CAI Yuan-qi,et al.Stability Analysis of Unsaturated Soil Slopes under Rainfall Infiltration[J].Rock and Soil Mechanics,2005,26(12):1957-1962.(in Chinese)

[20]Tohari A,Nishigaki M,Komatsu M.Laboratory Rainfallinduced Slope Failure with Moisture Content Measurement[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(5):575-587.

[21]Zhang J,Jiao J J,Yang J.In-situ Rainfall Infiltration Studies at a Hillside in Hubei Province,China[J].Engineering Geology,2000,57(1/2):31-38.

[22]Fredlund D G,Rahardio H.非饱和土土力学[M].陈仲颐,译.北京:中国建筑工业出版社,1997.

Fredlund D G,Rahardio H.Soil Mechanics for Unsaturated soil[M].Translated by CHEN Zhong-yi.Beijing:China Architecture and Building Press,1997.(in Chinese)

[23]凌华,殷宗泽,蔡正银.非饱和土的应力-含水量-应变关系试验研究[J].岩土力学,2008,29(3):651-655.

LING Hua,YIN Zong-ze,CAI Zheng-yin.Experimental Study on Stress-water Contentstrain Relationship of Unsaturated Soil[J].Rock and Soil Mechanics,2008,29(3):651-655.(in Chinese)

[24]毛昶熙,段祥宝,李祖贻,等.渗流数值计算与程序应用[M].南京:河海大学出版社,1999.

MAO Chang-xi,DUAN Xiang-bao,LI Zu-yi,et al.Numerical Computation in Seepage Flow and Programs Application[M].Nanjing:Hohai University Press,1999.(in Chinese)

[25]杨萍,朱占元.某震后高边坡含砾粉质粘土强度的正交试验研究[J].四川建筑科学研究,2012,38(4):119-122.

YANG Ping,ZHU Zhan-yuan.Orthogonal Experimental Study on Shear Strength of Gravel Silty Clay from a Post-earthquake High Slope[J].Sichuan Building Science,2012,38(4):119-122.(in Chinese)

Stability Analysis of Post-earthquake High Slope under Continuous Rainfall

ZOU Zu-yin1,2,ZHU Zhan-yuan1,2,ZHANG Feng3,CHEN Ting-ting1,2,ZHANG Zi-xing1,2

(1.College of Civil Engineering,Sichuan Agricultural University,Dujiangyan 611830,Sichuan,China;2.Sichuan Higher Education Engineering Research Center for Disaster Prevention and Mitigation of Village Construction,Dujiangyan 611830,Sichuan,China;3.School of Transportation Science and Engineering,Harbin Institute of Technology,Harbin 150090,Heilongjiang,China)

Continuous rainfall is an important factor inducing slope failure,and the causes of saturated-unsaturated slope failure under strong rainfall infiltration are diverse and complex.However,current research on the combined effects that induce slope failure is inadequate,particularly in relation to the increase in soil weight and softening of strength parameters after rainfall infiltration,both of which can impact slope stability.In this study,we establish a finite element model of a high slope following the Wenchuan earthquake in the condition of continuous rainfall.In the modeling process,the factors affecting slope stability caused by rainfall infiltration are considered,such as soil weight increase,penetration increase,and shear strength decrease.Furthermore,to analyze slop stability we employ a self-compiled calculation program,USLOPE-FEM,which is based on saturated-unsaturated seepage theory.Results show that the plastic strain zone of the slope is mainly distributed in the interface between the bottom of loosely accumulated materials and bedrock,and that the slope was close to a critical state of equilibrium before the rain.However,when the rainfall reached 20 mm/h,continuous infiltration increased the soil water content in the upper slope,the area of negative pressure disappeared,and a zone of saturated zone appeared.With continuation of rainfall,the transient saturated zone on the slope surface gradually developed towards the interior,causing a dramatic increase of in the weight and penetration of the slope soil,together with an evident decrease in shear strength.Furthermore,an integral increase of shear stress in the slope occurred and the plastic strain zone extended and interpenetrated gradually to the top of slope. After six hours of continuous rain,a local slump appeared on the surface of the free face,and after 36 hours the whole accumulation horizon gradually slumped along the bedrock and block river.Based on results of calculations and the above analysis,it is recommended that the slope is firstly improved and strengthened in relation to instability during continuous rainfall.It is considered that the results of this study can be used as a reference for evaluating slope safety under heavy rainfall.

slope engineering; heavy rainfall; stability analysis; saturated-unsaturated infiltration; Wenchuan earthquake

2016-01-23

四川省教育厅科研创新团队项目(16TD0006);青年基金项目(15ZB0001)；村镇建设防灾减灾四川省高等学校工程研究中心开放基金项目(CDPMV1405)

邹祖银(1974-)，男，博士研究生，副教授，主要从事边坡工程与岩土工程数值仿真方面的科研与教学工作。E-mail:382358357@qq.com。通信作者：朱占元(1974-)，男，博士，教授，主要从事冻土动力学与冻土工程、边坡工程方面的科研与教学工作。E-mail:zhuzyuan910@163.com。

P642.22

A

1000-0844(2016)04-0541-08

10.3969/j.issn.1000-0844.2016.04.0541