基础刚度对砖石古塔地震响应影响研究①

芦　苇,赵　冬,王玉兰

(1.西安建筑科技大学土木工程学院,陕西 西安 710054; 2.西安建筑科技大学理学院,陕西 西安 710054)



基础刚度对砖石古塔地震响应影响研究①

芦苇1,赵冬2,王玉兰1

(1.西安建筑科技大学土木工程学院,陕西 西安 710054; 2.西安建筑科技大学理学院,陕西 西安 710054)

以西安万寿寺塔纠偏工程为研究背景,分别建立增加圈梁、圈梁-地梁组合以及圈梁-地梁-托盘组合模型下的塔体与基础协同工作模型。采用时程分析法,对不同基础刚度条件下塔体的地震响应进行分析及评估,结果表明:(1)增大基础刚度的同时结构的地震位移响应将会被放大,但应力时程曲线的波动范围随之缩小、幅值减小;(2)增设圈梁时由于塔底三向受力,塔底应力将被放大;(3)进行基础完全托换能够大幅改善塔底在地震作用下的受力状态。在塔体加固维修时应综合考虑地震作用下塔体的位移放大效应与塔体应力分布的影响,选取合适的基础刚度。

砖石古塔; 基础刚度; 地震响应; 应力; 位移

0　引言

针对大多古建筑砖石结构自身基础刚度弱这类关键性结构缺陷,现有工程实例基础加固措施多采用在塔体底部增设圈梁,再设置地梁,最后安装托盘基础的加固方法[1-4]。但加固的塔体因基础刚度变化而引起抗震性能改变这类问题的研究,则尚未展开。

本文以西安万寿寺塔为研究背景,对纠偏加固后砖石古塔在不同基础刚度条件下塔体的地震反应变化进行对比分析。

1　工程概况

万寿寺藏经塔位于西安市东郊万寿中路,为市重点文物保护单位。该塔始建于万历年间(明),楼阁式,共6层,塔身通高22.5 m,平面呈六角形,青砖黄泥砌筑,底层实心。古塔多年向西北方向倾斜,近来倾斜加剧。为拯救岌岌可危的古塔,专家先暂时采用大型钢桁架支撑的方法阻止塔体倾斜趋势的发展,支撑设在塔重心点附近,即第3、第4层西北面,如图1(a);后经过研究制定纠偏加固措施,即钻孔掏土纠倾、基础加固、地基托换、整体顶升等工程措施,将古塔扶正,现处于安全状态[图1(b)]。

图1　万寿寺塔纠偏前后对比Fig.1　Comparison chart of the wanshou Tower before and after rectification

万寿寺塔的几何尺寸如表1所列。

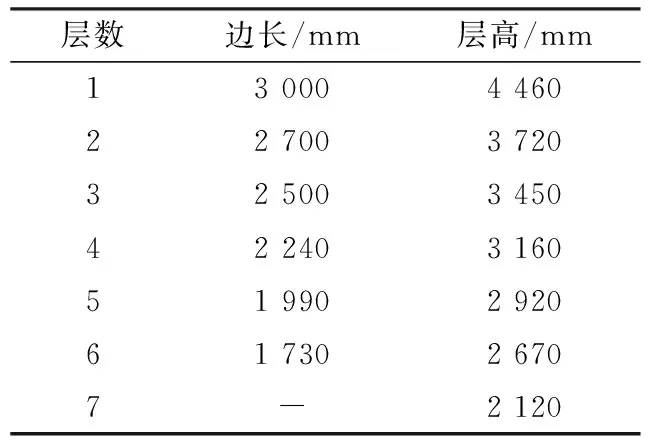
表1　万寿寺塔几何尺寸

2　动力测试

2.1动力测试方案

本工程采用脉动法[5]来测定分析结构物的动力特性。

(1)测试设备

选取DH5920动态信号测试分析系统,并通过DHMA实验模态分析系统对结构的模态参数进行动力特性分析;传感器采用磁电式水平速度传感器(型号为DH610H),频率范围0.1～100 Hz[6]。

(2)测点布置

采取同步测试法获得古塔的动力特性参数。此方法需在古塔各层布置传感器并同步采集脉动信号,以一层为一个固定参考点,每个测点均从南北和东西2个方向进行采样,每次采样30 min。各测点布置如图2所示。

(3)采样频率

现场测试原始信号的频率为30 Hz,采样频率取为100 Hz,主要分析万寿寺塔结构前4阶自振频率。

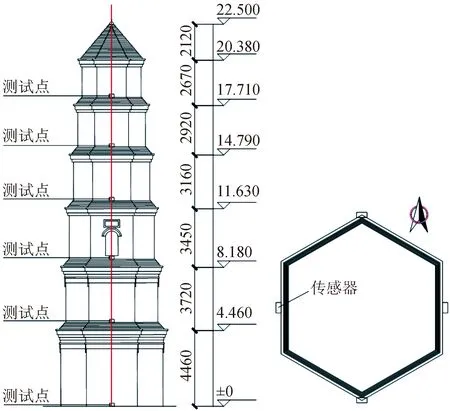
图2　测试点布置示意图Fig.2　Schematic diagram arrangement of test points

为减少传感器精度对实测结果的影响,实测前要对各传感器进行规一化验证,保证各个通道的反应是同方位的[6]。

(4)结构自振频率确定

利用DHMA实验模态分析系统对结构的模态参数进行分析,得到结构前4阶固有频率(表2)。

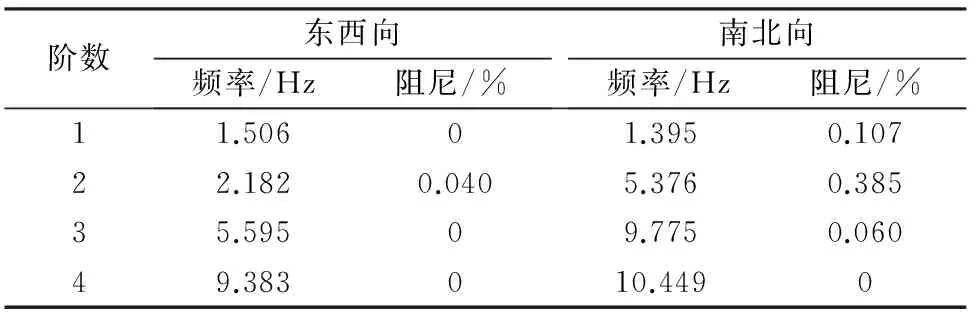
表2　阵型相关矩阵校验

3　数值模型

用反演法确定模型参数,即先拟定有限元模型材料属性,弹性模量E为待定参数,将有限元模型的模态分析结果与现场测试的整体动力特性结果加以对比,以结构周期T或频率为目标值。通过不断修改待定参数,使计算所得到的周期或频率与实测值(即动力测试结果)接近,得到塔体材料弹性模量E=900 MPa。

由此建立ANSYS模型,将结构前3阶振型同动力特性测试值结果相比较。由于脉动法测得的数据是与地基的相对值,在模型计算时只计算塔体模型(不加地基)。整理后的动力特性测试的数据与计算分析结果对比见表3。

表3　动力特性测试与模型计算频率值比较

前三阶频率与实测值相差不大,偏差来源于均质材料模型的简化、材料参数选取有限元网格划分及模型材料参数值的设定。因此认为此模型较好地反映了古塔结构的弹性阶段的材料性能,能够可靠模拟结构在地震作用下的状态。

4　地震响应分析

4.1基础刚度调整方案

(1)增设圈梁

按照工程加固古塔的实际情况,在上述模型塔底增设高400 mm的混凝土封闭圈梁加固,混凝土强度为C30。

(2)增设地梁

按照加固措施,加固圈梁后,再在塔底及圈梁下增设高900 mm的C30混凝土封闭地梁。

(3)增设托盘

在圈梁与垫梁的基础上,塔底增设高600 mm的C30混凝土托盘,托盘材料参数同圈梁。模型示意如图3。

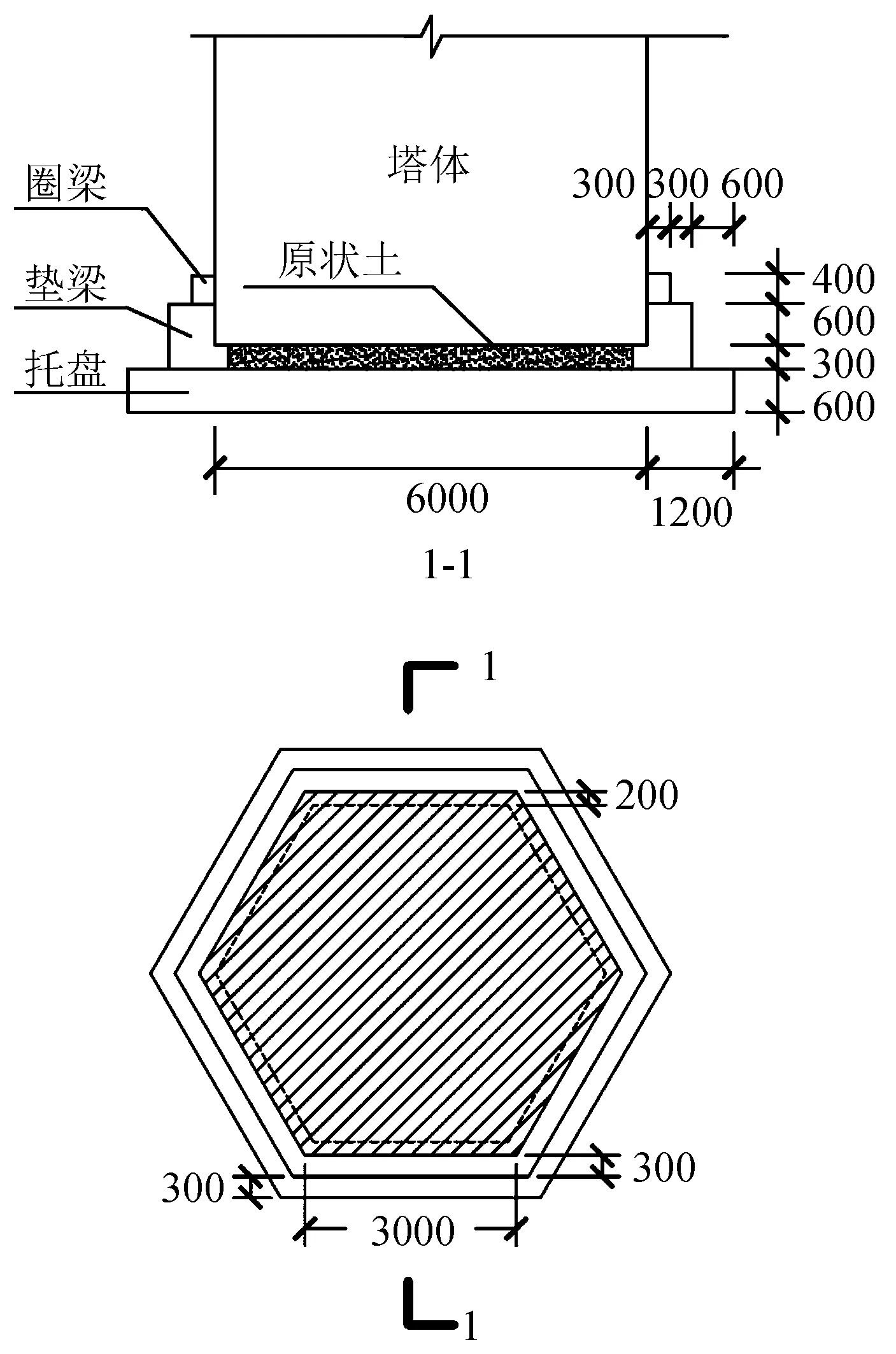
图3　不同基础刚度方案示意图Fig.3　Schematic diagram of different foundation stiffness

4.2地震波选取

根据万寿寺塔所处场地条件[7-8],建立地基与塔体协同工作模型。选取El-Centro波并进行调整,原始地震波特性如表4所列。应用时程分析法,对不同基础刚度条件下万寿寺在水平地震作用下的位移和应力状态进行分析。

表4　El-centro波主要特性

选取El-Centro波对塔体震害影响较大的前10 s,按照相应于Ⅷ度多遇地震将地震波峰值加速度调整为70 gal(图4)后作为地震动输入。考虑塔体的材料脆性及结构塑性变形能力较差,本文仅对古塔在弹性阶段的地震响应进行分析[9-10]。

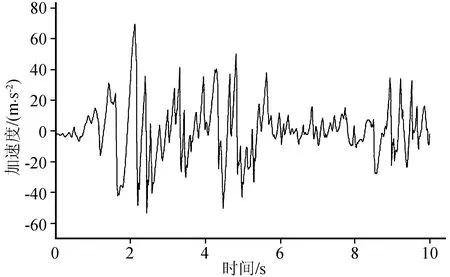
图4　调整后的El-Centro波加速度时程曲线Fig.4　Acceleration time-history curve of adjusted El-Centro wave

4.3不同基础刚度对塔体的地震反应分析

采用完全法对三种基础刚度条件的模型进行时程分析,考虑模型对称性,仅输入一个水平方向的El-Centro地震波,得到塔体水平位移响应。

(1)位移反应对比分析

由图5、图6及表5可看出,随着基础刚度增大,水平位移反应增加,增设托盘的位移最大,增设圈梁时位移最小,塔顶偏离塔体角度也随之增加,塔体的位移地震响应越明显。故随着塔体基础刚度变大,上部结构位移响应随之增大。因此在加固时应特别注意过大的基础刚度对结构地震位移响应的放大作用,注意实时监测及位移控制。

(2)应力响应对比

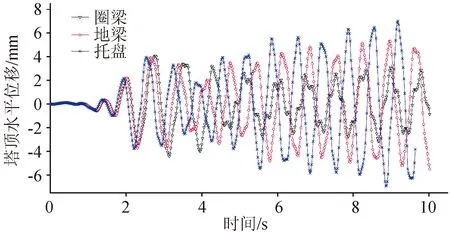
图5　不同基础刚度塔顶水平位移时程曲线Fig.5　Horizontal displacement time-history curve of tower top with different foundation stiffness

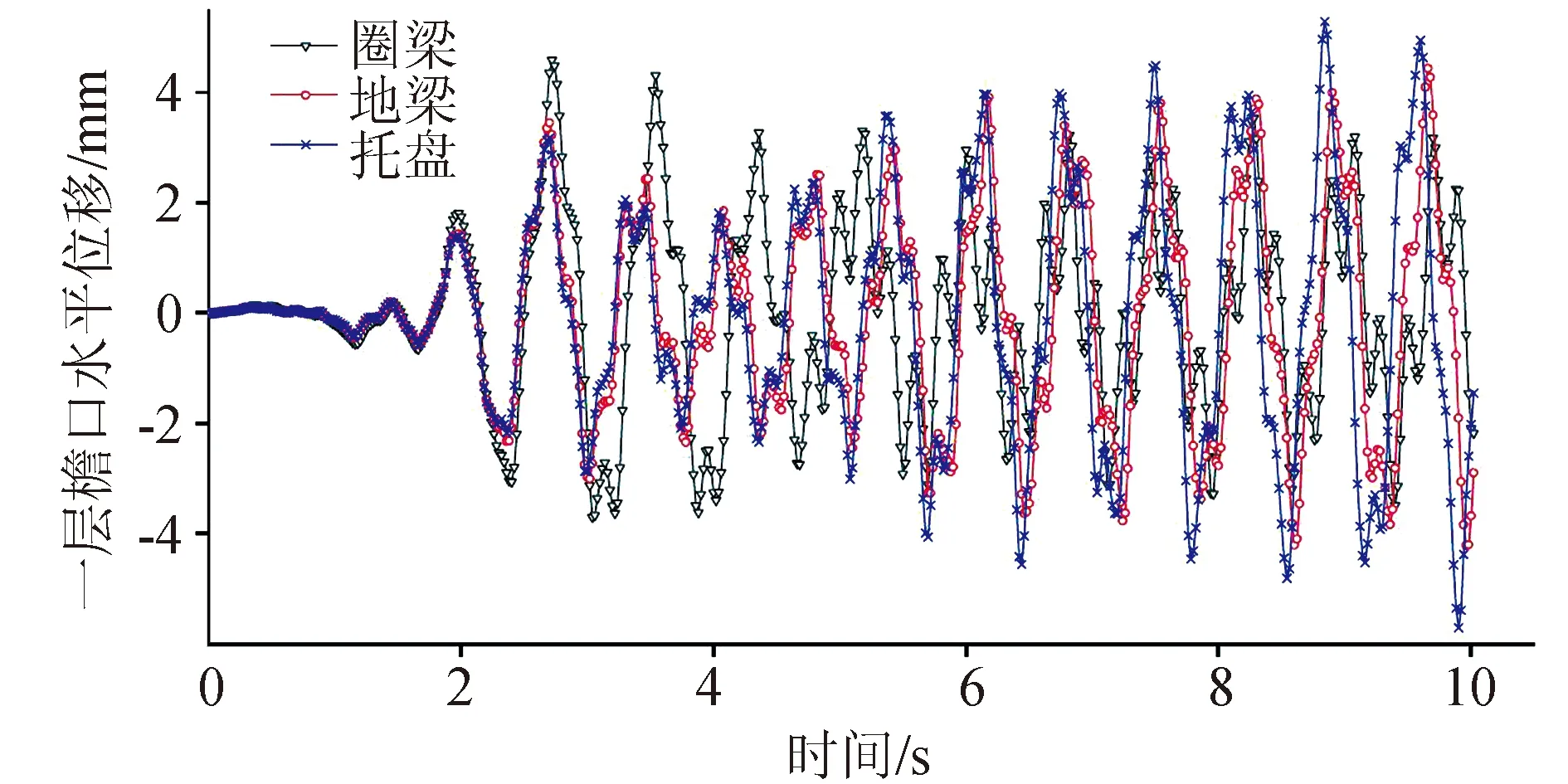
图6　不同基础刚度一层檐口水平位移时程曲线Fig.6　Horizontal displacement time-history curve of the first- floor cornice with different foundation stiffness

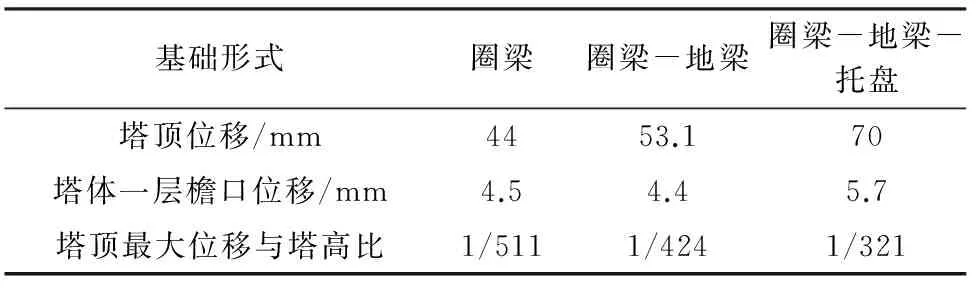
表5　塔体位移与塔高比

在塔体底部选取a、b两点(图7),提取塔体-基础-地基协同作用时三种基础刚度条件下a、b两点的第一、三主应力反应,分析其在地震波作用下的应力状态,并归纳a、b两点的主应力差值,即应力时程曲线的幅值,如表6所列。

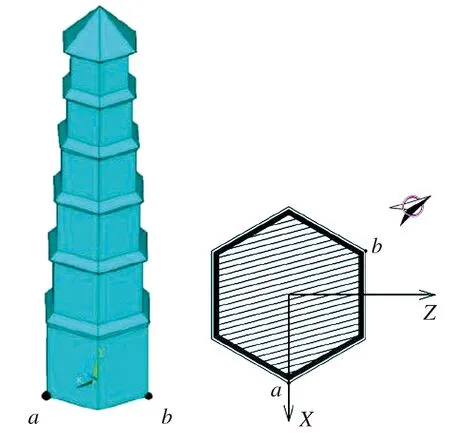
图7　a、b点位置示意图Fig.7　Location of test point a and b

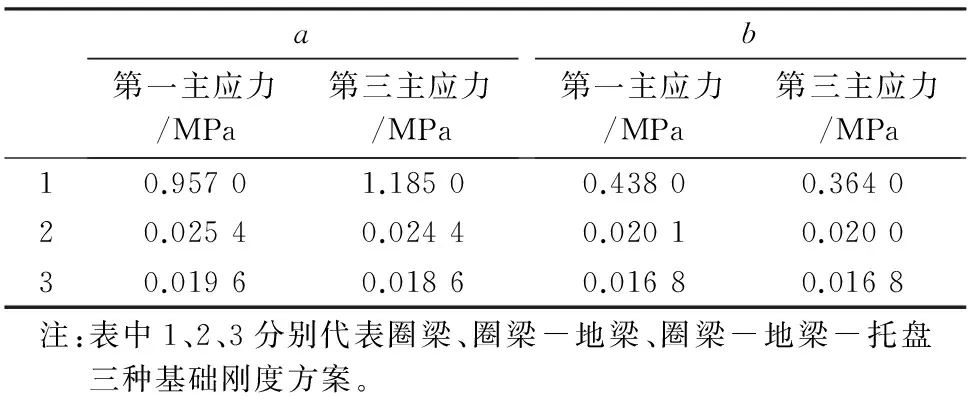
表6　不同基础刚度塔底应力幅值

随塔体基础刚度的增大,塔体a,b两点应力变化趋势基本相同,即主应力均随之减小。从图8～9看出,地震波作用下仅增设圈梁时塔底应力远大于其他两种基础刚度条件(应力值约为其他两种情况的40～50倍),这是由于仅用圈梁加固时,在三向受力状态下,“箍”效应下受地震力影响,应力峰值被放大。而从增设地梁到增设托盘这两种基础刚度条件下,转化为以“托换”产生的整体效应为主,随基础刚度增大,塔底应力分布趋于均匀,塔底角点的应力受基础刚度影响,使塔体底部受到的地震作用被削弱。这说明塔体基础加固,尤其是进行基础完全托换,将对塔体受力状态有很大改善。a、b两点主应力差值随塔体基础刚度的增大而减小,即塔体应力变化范围缩小(表6)。因此较大的基础刚度亦可减小地震作用下结构的应力变化幅值,防止出现局部因受力过大产生破坏。对基础进行完全托换能够从根本上避免结构因受地震造成的应力损伤。

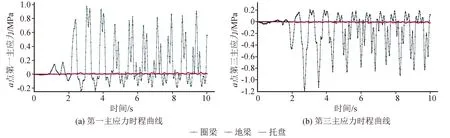
图8　不同基础刚度塔底a点第一、第三主应力时程曲线Fig.8　The first and third principal stress time-history curve of point a with different foundation stiffness

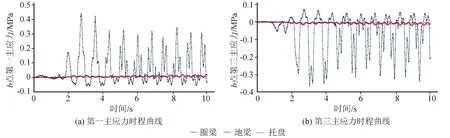
图9　不同基础刚度塔底b点第一、第三主应力时程曲线Fig.9　The first and third principal stress time-history curve of point b with different foundation stiffness

5　结论

基于时程分析法,选取El-Centro波并进行调整,建立基础为圈梁、圈梁-地梁组合及圈梁-地梁-托盘组合三种工况下的协同工作模型,进行地震响应分析,并提取塔顶、一层檐口水平向位移及塔底a、b点第一、第三主应力,分析其变化规律,结论如下:

(1)在水平单向地震波作用下,随着基础刚度增加,塔体水平向位移响应随之增大,塔体容易因位移过大发生破坏。基础刚度增大对塔体结构位移响应有放大作用。

(2)在水平单向地震波作用下,随基础刚度增加,塔体应力峰值减小,分布趋于均匀。当基础仅设置圈梁时,由于塔底处于三向受力状态,“箍”效应明显,在地震作用下应力反而增大,但在增设地梁和增设托盘这两种基础刚度条件下,应力时程曲线波动范围随基础刚度增大而缩小,应力反应幅值减小,塔体受到的地震作用削弱。这说明塔底应力对基础刚度条件敏感,较大的基础刚度能够削弱地震波作用下塔底的应力响应,避免结构因受地震力造成破坏。特别是进行基础完全托换,能够大幅改善塔底在地震作用下的受力状态。

(3)在对塔底基础进行加固时,应充分考虑地震作用下塔体的位移放大效应与塔体应力分布影响,选取合适的基础刚度方案。

References)

[1]陈平,赵冬,王伟,等.眉县净光寺塔纠偏工程[J].西安建筑科技大学学报,2003,35(1):44-47.

CHEN Ping,ZHAO Dong,WANG Wei,et al.A Study on the Rectification of Jingguang Temple Pagoda in Meixian Country[J].Journal of Xi'an University of Architecture and Technology,2003,35(1):44-47.(in Chinese)

[2]陈平,赵冬,王伟,等.眉县净光寺塔纠偏施工技术[J].施工技术,2003,32(6):24-25.

CHEN Ping,ZHAO Dong,WANG Wei,et al.Deviation Rectification Construction Technology for the Jingguang Temple Tower of Mei County[J].Construction Technology,2003,32(6):24-25.(in Chinese)

[3]袁建力,刘殿华,李胜才,等.虎丘塔的倾斜控制和加固技术[J].土木工程学报,2004,37(5):44-49.

YUAN Jian-li,LIU Dian-hua,LI Sheng-cai,et al.Inclination-control and Strengthening Technology Applied to Huqiu Pagoda[J].China Civil Engineering Journal,2004,37(5):44-49.(in Chinese)

[4]凌均安.组合纠偏法扶正兰州白塔[J].施工技术,1999,28(2):9-11.

LING Jun-an.Setting Lanzhou White Pagoda Upright with Combined Deviation Rectifying Method[J].Construction Technology,1999,28(2):9-11.(in Chinese)

[5]吴小波.某框架结构办公楼的动力特性测试与分析[J].福建建设科技,2005,10(5):29-30.

WU Xiao-bo.Dynamic Characteristics Test and Analysis of a Frame Structure Office Building[J].Fujian Construction Science and Technology,2005,10(5):29-30.(in Chinese)

[6]樊华,胡跃祥,袁建立.中江南塔结构动力特性测试研究[J].扬州大学学报:自然科学版,2013,16(3):57-60.

FAN Hua,HU Yue-xiang,YUAN Jian-li.The Structure of the South Tower of Zhongjiang in Dynamic Test Research[J].Journal of Yangzhou University:Natural Science Edition,2013,16(3):57-60.(in Chinese)

[7]薛峰,王庆良,胡亚轩,等.西安市岩土体剪切波速与土层深度关系的研究[J].地震工程学报,2014,36(2):249-256.

XUE Feng,WANG Qing-liang,HU Ya-xuan,et al.Study on the Relationship between Soil Depth and Shear Wave Velocity of Rock and Soil Mass in Xi'an City[J].China Earthquake Engineering Journal,2014,36(2):249-256.(in Chinese)

[8]陈昌禄,邵生俊,方娟,等.不同结构性黄土的强度规律及传统强度准则适应性分析[J].地震工程学报,2013,35(4):851-857.CHEN Chang-lu,SHAO Sheng-jun,FANG Juan,et al.Analysis of Strength Variation of Different Kinds of Structural Loess and Adaptability of Traditional Strength Criterion[J].China Earthquake Engineering Journal,2014,35(4):851-857.(in Chinese)[9]张名泉,马可婧,刘灿,等.不同掏蚀深度下古城墙的稳定性数值分析[J].地震工程学报,2013,35(1):133-138.

ZHANG Ming-quan,MA Ke-jing,LIU Can,et al.Analysis and Numerical Calculations of stability on Ancient City Wall under Various Sapping Depths[J].China Earthquake Engineering Journal,2013,35(1):133-138.(in Chinese)

[10]王旭东,石玉成,刘琨.夯土长城体掏蚀失稳机理研究[J].地震工程学报,2011,33(增刊):381-385.

WANG Xu-dong,SHI Yu-chen,LIU Kun.Research on Sapping Instability Mechanism for Rammed Wall[J].China Earthquake Engineering Journal,2011,33(Supp.):133-138.(in Chinese)

Impact of Foundation Stiffness on the Seismic Response of Ancient Masonry Pagoda

LU Wei1,ZHAO Dong2,WANG Yu-lan1

(1.School of Civil Engineering,Xi'an University of Architecture and Technology,Xi'an 710054,Shaanxi,China;2.School of Science,Xi'an University of Architecture and Technology,Xi'an 710054,Shaanxi,China)

Using the Wanshou Pagoda restoration project in Xi'an city as the research focus,this paper discusses the establishment of a cooperative work model for the pagoda body and foundations using three different types of foundation stiffnesses (setting ring beam,combination of ring beam and ground beam,and combination of ring beam,ground beam and tray).Field tests are conducted to determine the dynamic characteristics of the pagoda body using the pulsating method,and results are used as a reference for verifying the reliability of the simplified numerical model.Seismic waves (EL-Centro)under the same site conditions are selected as the horizontal excitation acting on the foundation.With an understanding of the pagoda's brittleness,this paper analyzes only the dynamic response in the elastic stage.A time-history analysis method is used to analyze the stress and displacement response law under different foundation stiffness conditions,and during displacement analysis the top of pagoda and 1F eave are selected as displacement monitoring points.The maximum horizontal displacement is found to increase with an increase in foundation stiffness,and the dip angle of the pagoda correspondingly increases.For stress analysis,two points,"a" and "b",from the pagoda bottom are selected as monitoring points,and the first and third principal stress-time curves of the two points are analyzed with different foundation stiffnesses.With an increase in foundation stiffness,the first and third principal stress at point "a" drops significantly,and the stress change trend at point "b" is similar to that at "a".It should be noted that when only the ring beam is set,the peak stress at the pagoda bottom is about 40～50 times that of the other foundation forms.The analysis results show that:(1)with an increase in foundation stiffness there is amplification of the seismic displacement response of the pagoda structure,but a reduction in the fluctuation range of the stress time-history curve; (2)the stress state of the pagoda bottom is sensitive to foundation stiffness,and as the pagoda bottom is in a tri-axial stress state when the ring beams are added its stress is magnified; (3)underpinning the entire foundations would significantly improve the stress state of pagoda bottom under seismic action,and also have a positive effect on the shear stress control of the pagoda body.However,when reinforcing the pagoda body and determining the appropriate foundation stiffness,it is necessary to comprehensively consider the displacement amplification effect of the pagoda body,and the stress distribution of pagoda bottom under seismic action.

ancient masonry pagoda; foundation stiffness; seismic response; stress; displacement

2015-07-08

芦苇(1988-)，男，陕西延安人，博士研究生，从事古建筑加固及维修工程研究。E-mail：281081454@qq.com。

TU746.3

A

1000-0844(2016)04-0498-06

10.3969/j.issn.1000-0844.2016.04.0498