含缺陷结构的冲击断裂试验研究

杨仁树， 丁晨曦， 杨立云， 陈　程， 孙金超

(1．中国矿业大学(北京)力学与建筑工程学院，北京　100083； 2. 深部岩土力学与地下工程国家重点试验室，北京　100083)



含缺陷结构的冲击断裂试验研究

杨仁树1,2， 丁晨曦1， 杨立云1， 陈程1， 孙金超1

(1．中国矿业大学(北京)力学与建筑工程学院，北京100083； 2. 深部岩土力学与地下工程国家重点试验室，北京100083)

利用新型数字激光动态焦散线试验系统和落锤冲击加载平台，以缺陷端部曲率为单一变量，将孔状缺陷和裂纹缺陷纳入同一个试验研究体系。研究了冲击荷载下，含不同端部曲率中央缺陷的PMMA条形试件的三点弯曲动态断裂过程，断裂破坏经历三个阶段：前期为冲击应力波作用下，试件下边界裂纹的起裂与扩展；中期为裂纹在缺陷处的应力释放和停滞；后期为落锤自重作用下，缺陷端部的起裂与试件贯穿。在相同的试验条件下，不同端部曲率的缺陷对前期裂纹起裂与扩展基本没有影响；缺陷端部曲率越大，中期缺陷处停滞时间越短，并得出二者之间的近似函数关系；后期缺陷端部起裂时的应力强度因子随着缺陷端部曲率的增大呈现出先减小后增大的变化趋势。

动态焦散线；冲击荷载；缺陷；曲率；应力强度因子

在多数工程结构中，缺陷(如裂纹、孔洞)的存在是不可避免的，这些缺陷的存在对工程结构的强度、抗震性能等有着严重的影响。对含缺陷结构的断裂行为的研究一直以来都是断裂力学、岩石力学等学科领域的重点关注课题。在理论方面，任利等[1]提出了复合型裂纹断裂的新准则，指出复合裂纹的扩展规律与裂纹即时的应力状态有关；Wasiluk等[2]建立了Z准则，认为裂纹扩展方向可以被最小Z因子进行确定；张娅等[3]利用弹塑性大挠度模型并结合有限差分法分析了含缺陷自由梁受冲击荷载的动力行为；胡家顺等[4]根据线性断裂力学理论和应变能释放原理得出了管道中的裂纹缺陷对结构固有频率的影响规律；在试验方面，岳中文等[5]研究了介质中的裂纹缺陷对爆炸荷载的动态响应；杨仁树等[6]研究了冲击荷载作用下二维介质中裂纹的倾角对结构破坏的影响；李术才等[7]研究了三维介质中裂纹倾角对类岩石材料断裂特征的影响。

可以发现，人们较多研究的是裂纹缺陷对结构力学性能的影响，孔状缺陷的相关研究较少，但实际结构物中，不规则孔状缺陷却是客观存在、不容忽视。此外，对于裂纹缺陷的起裂，可以通过Griffith[8-9]的相关理论进行求解裂纹尖端的应力场；而对于孔状缺陷的起裂，却一直没有比较适合的理论加以解释。且由于材料内部缺陷的多样性和随机性，研究存在较大的难度，以至此领域的研究并没有形成定论[10]。

基于此，希望能够建立裂纹缺陷和孔状缺陷对结构力学性能影响的内在联系。一定意义上来说，缺陷端部的曲率是建立孔状缺陷与裂纹缺陷之间联系的物理量，孔状缺陷端部曲率为有限值，裂纹缺陷端部曲率远大于孔状缺陷的，理想裂纹端部的曲率趋于无穷大。结合动态焦散线试验方法，通过模型试验的手段研究含不同端部曲率缺陷对结构冲击断裂特性的影响，从试验角度，将裂纹缺陷和孔状缺陷的研究纳入同一体系，为进一步的深入研究提供了思路。

1　试验原理与试验系统

1.1焦散线试验原理

焦散线试验方法自1964年由Manogg[11]提出至今，已经获得长足发展，其中透射式焦散线试验方法已经成为研究PMMA等透明材料断裂问题的可靠方法。国内苏先基等[12]率先采用多火花式高速摄影机对动荷载作用下裂纹的动态扩展问题进行了研究；杨仁树等[13]基于焦散线原理建立了新型数字激光动态焦散线试验系统。

图1为焦散线方法原理示意图[14]，在拉、压应力作用下，固体介质会发生形变，导致厚度方向上的尺寸变化，进而影响其折射率。平行光线透射介质时，在不同折射率的区域会发生不同方向的折射，在参考平面上形成焦散线及其包围的焦散斑(暗区)，裂纹尖端处于

焦散斑的中心处。

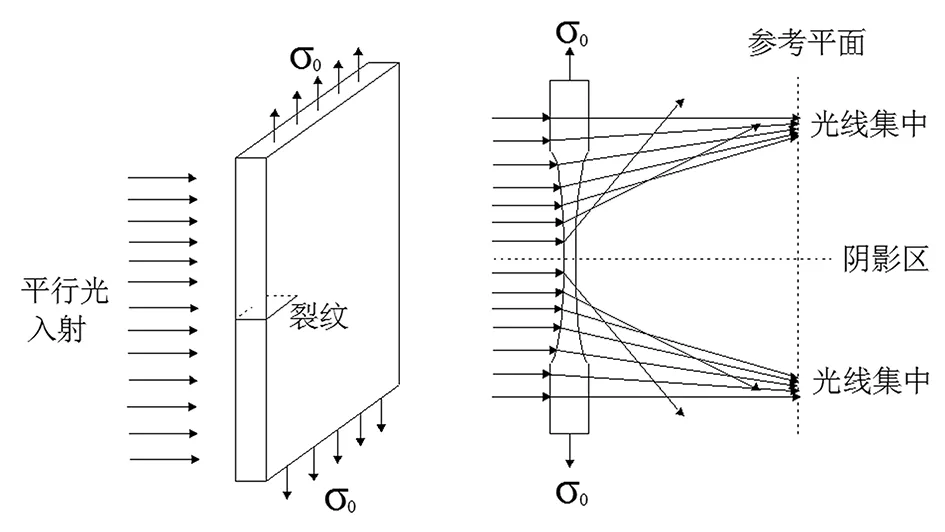
图1　焦散线方法原理图Fig.1 Diagram of caustics

在焦散线试验中，裂纹尖端的应力强度因子可以将相关焦散斑特征尺寸代入计算式[15]获得，计算式如下：

KⅡ=μKⅠ

(1)

式中：Dmax为焦散斑最大直径；μ为比例系数，与焦散斑的最大直径Dmax和最小直径Dmin有关；g为数值系数，通常取g=3.02。F(ν)是由裂纹扩展速度引起的修正因子。数值分析发现，在具有实际意义的扩展速度下，F(ν)≈1。对于本试验而言，试件的有效厚度deff=5 mm，应力光学常数c=85 μm2/N，参考平面到试件平面的距离z0=900 mm。

1.2试验设备

该试验所采用的试验设备为动态光测力学实验室的新型数字激光动态焦散线方法试验系统和落锤冲击加载试验平台，图2为该试验系统的光路图，图3为落锤冲击加载试验平台。

图2 新型数字激光动态焦散线方法试验系统光路图Fig.2BeampathdiagramofDLDC图3 落锤冲击加载平台Fig.3Drop-hammerimpacttestingplatform

2　PMMA试件与试验操作

2.1PMMA试件及其规格参数

试验的模型材料为PMMA板材，PMMA为典型的脆性材料，具有较高焦散光学常数，且是光学各向同性材料，作为模型材料用于研究冲击断裂[6,16-17]、爆炸致裂[5,18]的作用机理由来已久。PMMA的动态力学参数为: 膨胀波波速CP=2 320 m/s，剪切波波速CS=1 260 m/s，动态弹性模量Ed=6. 1 GN/m2，动态泊松比νd=0.31，动态应力光学常数|Ct|=85 μm2/N。

如图4所示，试件的规格为200 mm×50 mm×5 mm，试件的下方中点处均预制一条垂直于上、下边界的切缝，长度为5 mm，切缝端部记为点O，预制该切缝的目的是为了保证在落锤冲击荷载下，引导试件均能从下边界中部起裂，保证起裂的一致性。前5组试件中央分别预制半长轴a=5 mm，半短轴b=5 mm，4 mm，…，1 mm的椭圆形孔状缺陷，依次对应的组编号为S-1，S-2，…，S-5；第6组试件中间预制一条长为2a=10 mm的激光切缝，组编号为S-6。缺陷下端点记为点P1，上端点记为点P2，试件共6组，每组3个，共计18个。

图4　试件及加载示意图Fig.4 Diagram of specimen and loading

椭圆的长轴端点处的曲率为：

(2)

式中：κ为长轴端点处的曲率；a为半长轴长度；b为半短轴长度。

将a,b值代入式(2)计算可得出前5组试件缺陷上、下端部(P2、P1)处的曲率分别为20 m-1、31 m-1、56 m-1、125 m-1、500 m-1。其中试件组S-6中部的缺

陷是一条激光切缝，其端部是以激光线度(0.3 mm)为直径的圆弧，端部曲率为6 667 m-1，远大于前5组的，可视为裂纹缺陷。随着椭圆端部曲率的逐渐增大，孔状缺陷逼近裂纹缺陷。

2.2试验操作及数据处理

试验采用落锤冲击加载，加载点为试件上表面中点。为了减小实验装置惯性效应和防止接触点提前破坏，经过试验的调试对比，最终确定落锤重1 kg，自由下落高度300 mm，获得加载速度2.42 m/s，能够满足试验要求，6组共18个试件的加载条件相同。在落锤开始下落的同时，触发高速摄影仪，保证整个加载过程能够被完整的记录。高速摄影仪的图片拍摄频率为150 000 fps，即每秒拍摄150 000幅图片，相邻两幅图片之间的时间间隔为极短的6.67 μs。采用Photoshop软件处理图片，获取焦散斑的相关特征尺寸，代入式(1)计算得到各瞬时时刻的应力强度因子。

3　试件断裂形态与分析

3.1断裂形态

6组共18个试件加载完成以后，通过对试验结果的观察和相关数据的处理，发现组内试件的破坏特性基本一致，说明试验操作稳定，试验结果可靠。每组随机抽取1个试件进行分析，图5所示的是6个试件的断裂形态，裂纹的整体扩展轨迹为直线，断裂面平整光滑。

图5　试件断裂形态Fig.5 Fracture morphology of specimens

3.2时程特征分析

由于篇幅所限，图6只列出了试件S-1-1、S-4-1、S-6-1这3个试件断裂过程的焦散照片及对应时间。试验的冲击过程被高速摄影仪完整记录，试验过程中落锤始终与加载点接触，无二次冲击。将落锤冲击接触试件上表面的时刻记为0 μs，冲击作用下，预制切缝O处发生应力集中，根据式(1)，可定性了解到应力强度因子与焦散斑尺寸Dmax呈现正相关关系， 焦散斑尺寸逐渐变大，则应力强度因子也随之增长。当应力强度因子超过该试验条件下的断裂韧性值(临界应力强度因子)，O处即发生起裂，图中所示试件在307 μs左右起裂。随后，裂纹快速扩展，360 μs左右扩展至缺陷下端部P1处，在P1处焦散斑逐渐减小直至完全消失。不久，缺陷上端出现“月牙形”散斑，缺陷上端部P2处发生应力集中，随着应力集中程度的加剧，P2处开始起裂，观察发现，不同端部缺陷的试件在P2处起裂的时间存在明显差异。此后，裂纹扩展直至试件贯穿。

图6　试件破坏各阶段焦散照片Fig.6 Digital caustic photos of specimens in different fractural stages

通过观察分析发现，在冲击荷载作用下，试件的断裂破坏具有三个不同阶段：

前期：落锤冲击加载，试件下边界预制切缝O处发生应力集中并起裂，裂纹扩展至缺陷下端P1处。中期：裂纹扩展至缺陷处，停滞。后期：缺陷上端P2处发生应力集中并起裂，裂纹继续向落锤加载位置扩展，直至贯穿试件。在整个裂纹扩展阶段，焦散斑形状对称，始终呈现为Ⅰ型拉伸破坏的典型形状，因此，试件的主要断裂形式为拉伸破坏。

表1、表2分别列出了6组试件断裂破坏的主要时间历程和前、中期时间。可以发现，6组试件在相同冲击荷载作用下，O处起裂的时间t1和裂纹扩展至缺陷下端P1处的时间t2均基本相同，t1为307 μs左右，t2为360 μs左右，前期O至P1的扩展时间(t2-t1)为53 ～60 μs左右。据此，可以从断裂破坏的时程特征上判断，试件中缺陷端部曲率的变化并不引起前期裂纹起裂及扩展的明显变化。

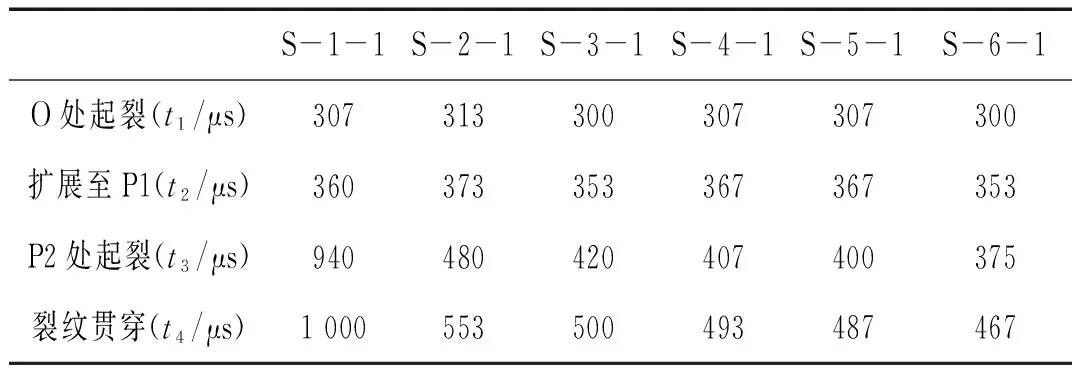
表1　试件断裂破坏主要时间历程表

表2　试件断裂破坏前、中期时间表

此后，裂纹扩展至缺陷处，进入中期停滞阶段，随后缺陷上端P2处起裂，进入破坏后期；P2处起裂时间t3和贯穿时间t4则表现很大的差异性，显然这是试件中缺陷的不同造成的。随着试件中的缺陷上端P2处的曲率的增加，裂纹在缺陷处的停滞时间△t=(t3-t2)迅速减小；表明缺陷端部曲率的增加促使缺陷端部应力积聚加剧，进而缩短起裂时间。根据缺陷曲率κ与停滞时间△t的对应关系，利用非线性拟合得到二者之间的近似函数关系为：

(3)

3.3应力特征分析

由于试件中央缺陷的存在，裂纹扩展至缺陷处出现停滞，据此，将各试件的裂纹尖端应力强度因子KⅠ与时间t的关系分为两部分表示。图7(a)为各试件从O处发生应力集中至裂纹扩展到P1处的KⅠ-t图像，图7(b)为各试件从P2处起裂至裂纹贯穿试件的KⅠ-t图像。

图7　试件断裂破坏的KⅠ—t图像Fig.7 Curves of KⅠ—t during fracture

通过对图7的分析发现，在开始加载到断裂破坏的前期阶段(0～307 μs)，各个试件的裂纹尖端应力强度因子大小及变化趋势基本一致。表3为各试件扩展裂纹在O、P1、P2三个指定位置处的应力强度因子值，其中O处起裂时的应力强度因子即为该加载条件下的动态断裂韧性值，可以看出，对于含不同缺陷的试件，O处起裂的临界应力强度因子基本相同，KⅠ为0.72 MN/m3/2左右；裂纹扩展至P1处时，应力强度因子基本相同，KⅠ为0.87 MN/m3/2左右。进而从应力特征角度说明了试件中缺陷端部曲率的变化并不引起初期裂纹起裂及扩展的明显变化，这与前文从时程特征角度分析所得到的结论是一致的。

在落锤冲击作用下，预制切缝端部O处最先发生应力集中，O处焦散斑随着时间推移逐渐变大，应力强度因子值逐渐增长，这是起裂之前能量积聚的阶段，当应力强度因子值达到动态断裂韧性值，O处裂纹起裂并扩展；在裂纹由O扩展至P1过程中，试件中反射、绕射应力波与裂纹发生复杂的相互作用，运动裂纹端部的应力集中被进一步加强，应力强度因子进一步上升。随后，裂纹扩展至缺陷处，裂纹端部的应力集中释放，裂纹扩展停滞。落锤冲击加载时间约为200 μs，经过前期的裂纹扩展和中期在缺陷处的停滞，冲击应力波在试件边界和中央缺陷处多次来回反射和绕射，应力波的能量衰减殆尽；后期缺陷上端部P2处的起裂和扩展可视为在落锤自重作用下的破坏，缺陷端部起裂后，应力强度因子迅速减小，无明显波动，符合准静态加载裂纹端部应力强度因子的变化规律。

表3　各试件在指定位置处的应力强度因子

从表3列出的各个试件的缺陷上端部P2处起裂时的裂纹尖端应力强度因子值，可以看出，各个试件的缺陷上端部P2处起裂时的应力强度因子差别较大。其中，随着缺陷端部曲率的增加，P2处起裂时的动态应力强度因子逐渐减小(前5组S-1～S-5的试验结果表现出这样的趋势)，而S-6试件缺陷上端部点P2处起裂时的动态应力强度因子较之则表现为逆势增大(由于试验技术的限制，难以在组S-5和S-6之间插入端部缺陷介于二者之间的试验组来进一步细分曲率变化的梯度)。图8为通过缺陷曲率和P2处起裂的应力强度因子对应值拟合的曲线，可见，在该试验条件下，随着缺陷端部曲率的增大，P2处起裂时的应力强度因子在一定范围内表现为先减小后增大。在后期的研究中，将进一步从力学和能量角度对这一现象作出详细解释。

图8　P2处起裂的KⅠ—κ图像Fig.8 Crack initiation curves of KⅠ—κ at P2

4　结　论

以缺陷端部曲率为单一变量，将孔状缺陷和裂纹缺陷纳入一个试验研究体系。

前期阶段的预制切缝处起裂的裂纹在扩展过程中应力强度因子逐渐增大；中期阶段裂纹扩展至中央缺陷处，经历能量释放和停滞；后期阶段的缺陷端部起裂的裂纹在扩展过程中应力强度因子迅速减小。试件断裂形式主要为Ⅰ型拉伸破坏。

[1] 任利，朱哲明，谢凌志，等．复合型裂纹断裂的新准则[J]．固体力学学报，2013，34(1):31-37.

REN Li，ZHU Zhe-ming， XIE Ling-zhi， et al． New fracture criterion for mixed mode cracks[J]． Chinese Journal of Solid Mechanics， 2013，34(1):31-37.

[2] Wasiluk B, Golos K． Prediction of crack growth direction under plane stress for mixed-modeⅠandⅡloading[J]． Fatigue & Fracture of Engineering Materials & Structures， 2000， 23(5):381-386．

[3] 张娅，江志农，赵军．含缺陷自由梁的弹塑性大挠度动力响应[J]．振动与冲击，2007，26(10):27-29.

ZHANG Ya， JIANG Zhi-nong， ZHAO Jun． Elasto-plastic dynamic behaviour of a free-free beam with an initial notch[J]． Journal of Vibration and Shock， 2007，26(10):27-29.

[4] 胡家顺，冯新，周晶． 含非贯穿直裂纹管道的振动特性分析[J]．振动与冲击，2011，30(4):21-25.

HU Jia-shun， FENG Xin， ZHOU Jing． Vibration analysis and crack identification of a cantilever pipe with a circumferential part-through crack[J]． Journal of Vibration and Shock， 2011，30(4):21-25.

[5] 岳中文，杨仁树，郭东明，等．爆炸应力波作用下缺陷介质裂纹扩展的动态分析[J]． 岩土力学，2009，30(4):949-954.

YUE Zhong-wen， YANG Ren-shu， GUO Dong-ming， et al． Dynamic analysis of crack propagation in media containing flaws under the explosive stress wave[J]． Rock and Soil Mechanics， 2009，30(4):949-954.

[6] 杨仁树，王雁冰，侯丽冬，等．冲击荷载下缺陷介质裂纹扩展的DLDC试验[J]．岩石力学与工程学报，2014，33(10):1971-1976.

YANG Ren-shu， WANG Yan-bing， HOU Li-dong， et al． DLDC experimental on crack propagation in defective medium under impact loading[J]． Chinese Journal of Rock Mechanics and Engineering， 2014，33(10):1971-1976.

[7] 李术才，杨磊，李明田，等．三维内置裂隙倾角对类岩石材料拉伸力学性能和断裂特征的影响[J]． 岩石力学与工程学报，2009，28(2):281-289.

LI Shu-cai， YANG Lei， LI Ming-tian， et al． Influences of 3d internal crack dip angle on tensile mechanical properties and fracture features of rock-like material[J]． Chinese Journal of Rock Mechanics and Engineering， 2009，28(2):281-289．

[8] Griffith A A． The phenomena of rupture and flow solids [J] ． Philosophical Transactions of the Royal Society of London， Sereis A， 1921， 221: 163-198.

[9] Tada H， Par is P C， Irwin G R． The stress analysis of cracks handbook， 3rd edition [M]． New York:ASME． 2000.

[10] 朱乃龙，饶云刚，余舟波．脆性材料统计断裂判据的研究[J]．工程力学，2009，26(5):35-47.

ZHU Nai-long， RAO Yun-gang， YU Zhou-bo． Study on criterion of statistical fracture for brittle materials[J]．Engineering Mechanics， 2009，26(5):35-47.

[11] Manogg P． Anwendung der schattenoptik zur untersuchung des zerreissvorgangs von platen[D]．West Germany: University of Freiburg，1964.

[12] 苏先基，雷志辉． 动态焦散线试验方法及其在断裂力学中的初步应用[J]．力学学报，1987，19(4):357-365.

SU Xian-ji， LEI Zhi-hui． Experimental methods of dynamic caustics and its application in fracture mechanics[J]． Acta Mechanica Sinica，1987，19(4):357-365.

[13] 杨立云，杨仁树，许鹏． 新型数字激光动态焦散线试验系统及其应用[J]．中国矿业大学学报，2013，42(2):188-194.

YANG Li-yun， YANG Ren-shu， XU Peng． Caustic method combined with laser & digital high-speed camera and its application[J]． Journal of China University of Mining & Technology， 2013，42(2):188-194．

[14] Takahashi K， Arakawa K ．Experimental mechanics， dependence of crack acceleration on the dynamic stress intensity factor in polymers[J]． Experimental Mechanics， 1987，27(6):195-217.

[15] Theocaris P S． Dynamic propagation and arrest measurements by method of caustics on overlapping kewparallel cracks[J]．International Journal of Solid and Structures，1978(14):639-653.

[16] 李清，张迪，杨阳，等．含单侧预制裂纹梁的冲击动态断裂过程试验研究[J]．振动与冲击，2015，34(4):205-210.

LI Qing， ZHANG Di， YANG Yang， et al． Dynamic fracture tests for a beam containing unilateral pre-existing cracks under impact loads[J]． Journal of Vibration and Shock， 2015，34(4):205-210.

[17] 姚学锋，熊春阳，方竞．含偏置裂纹三点弯曲梁的动态断裂行为研究[J]．力学学报，1996，28(6):661-669.

YAO Xue-feng， XIONG Chun-yang， FANG Jing． Study of dynamic fracture behavior on three-point-bend beam with off-center edge-crack[J]． Acta Mechanica Sinica， 1996，28(6):661-669.

[18] 李清，杨仁树．爆炸载荷裂纹扩展的应力强度因子及其断裂行为[J]．煤炭学报，2002，27(3) ：290-293.

LI Qing，YANG Ren-shu．Stress intensity factor and fracture behavior for crack propagation under blasting load[J]．Journal of China Coal Society，2002，27(3)：290-293．

Tests for structures with flaws under impact loading

YANG Renshu1,2, DING Chenxi1, YANG Liyun1, CHEN Cheng1, SUN Jinchao1

(1. School of Mechanics and Civil Engineering, China University of Mining and Technology, Beijing 100083, China;2. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Beijing 100083, China)

Using the test system of digital laser dynamic caustics(DLDC) and the impact loading platform of drop hammer, hole and crack flaws were introduced into the same test study system with a single variable of flaw tips curvature. Dynamic three-point bending tests of PMMA strip specimens with different tips curvatures of flaws under impact loading were studied. It was shwon that fracture failure experiences three stages including crack initiation and propagation at bottom border of specimens duo to impact stress wave action during initial stage, stress release and crack stagnation at flaws during medium stage, and crack initiation at top tips of flaws and specimens penetration duo to the weight of drop hammer during ultimate stage; under the same test conditions, changes of curvature at flaw tips almost have no effect on crack initiation and propagation during initial stage; stagnation time is shortened with increase in curvature at flaw tips during medium stage, the approxinate function relation between them is obtained; the stress intensity factors of crack initiation at flaw tips decreases firstly and then increases with increase in curvature during ultimate stage.

dynamic caustics; impact loading; flaw; curvature; stress intensity factor

国家自然科学基金-煤炭联合基金重点项目(51134025)；深部岩土力学与地下工程国家重点实验室自主重点课题(GDUEZB201401)

2015-10-28修改稿收到日期：2016-01-14

杨仁树 男，教授，1963年生

丁晨曦 男，博士，1991年生

E-mail:dingcx91@sina.com

O348.1

A

10.13465/j.cnki.jvs.2016.15.017