消能限位防屈曲支撑拟静力试验研究

马　华, 张芳亮, 刘亚双, 李振宝

(北京工业大学 城市与工程安全减灾省部共建教育部重点实验室，北京　100124)



消能限位防屈曲支撑拟静力试验研究

马华, 张芳亮, 刘亚双, 李振宝

(北京工业大学 城市与工程安全减灾省部共建教育部重点实验室，北京100124)

提出了一种具有限位功能的新型防屈曲支撑(LBRB)，该支撑在普通防屈曲支撑上设置限位装置，实现小变形时正常发挥防屈曲支撑的耗能作用，大变形时防屈曲支撑的外约束体提供附加刚度，限制变形的进一步发展。通过6个LBRB构件的拟静力试验，研究限位距离、工作段截面积、工作段长度、钢芯与夹持钢管之间间隙等因素对滞回性能的影响，结果表明：构造合理的LBRB构件具有良好的耗能能力并能在大变形时提供附加刚度。

防屈曲支撑；耗能作用；限位；附加刚度；滞回性能

北岭地震和阪神地震后，日本、美国和台湾地区对防屈曲支撑的研究日趋广泛[1-2]。近些年，大陆地区对防屈曲支撑的研究逐渐成熟，研究了材料、约束形式、间隙、无黏结材料等对防屈曲支撑性能的影响[3-4]。防屈曲支撑兼备普通支撑和阻尼器的优点，在小震作用下为结构提供侧向刚度，中震、大震作用下可由钢芯屈服耗散地震能量[5-8]。

随着经济的发展，由位移起控制作用的高层、超高层结构日趋常见，控制其在大震、超大震作用下的过大变形是亟待深入研究的重要课题[9,10]。韩淼等[11]提出基础隔震层软碰撞限位的思想，将隔震层变形限制在允许变形范围内。王军文[12]考虑相邻梁体相对位移的不同因素，提出在桥梁中抗震限位装置设计方法的研究。闫维波等[13]对比设置和未设置限位斜撑RC耗能器框架的抗震性能，证明耗能器屈服可消耗部分地震能量，而限位斜撑大幅提高了结构后期承载力。万金国等[14]针对普通防屈曲支撑的单一屈服点不能适应不同水平地震作用以及在变形过大时容易断裂的问题，提出过一种具有双屈服点和免断裂功能的防屈曲支撑，但对大变形时的性能尚不明确。

本文在保证普通防屈曲支撑耗能能力的基础上，开发其限位功能，研发一种消能限位防屈曲支撑(简称LBRB)，用于高层、超高层结构的减震控制，在明确结构系统构造并进行力学性能分析的基础上，对LBRB构件进行拟静力试验，研究限位距离、工作段参数等对其耗能、限位性能的影响，建立其恢复力模型，为设计提供参考。

1　LBRB基本力学性能

LBRB由钢芯、夹持钢管及限位装置构成，钢芯屈服变形达到限位装置设置的限位距离前，LBRB与普通防屈曲支撑没有差别。钢芯变形达到限位距离后，夹持钢管参与轴向受力，提供附加刚度。此时，LBRB退化为钢芯与夹持钢管并联的中心支撑构件。

为分析LBRB的工作原理，将钢芯工作段单元及夹持钢管视为并联的弹塑性弹簧单元；外部约束钢管对刚度及承载能力的提高可通过钩单元(只受拉力)及缝单元(只受压力)模拟；连接段及过渡段视为弹性弹簧。LBRB的力学模型如图1所示。

LBRB的刚度会随钢芯与夹持钢管的受力状态而改变，表1为不同阶段LBRB刚度公式。其中kw为钢芯工作段弹性刚度，kc为钢芯连接段弹性刚度，kt为夹持钢管弹性刚度，α为屈服系数，即屈服后刚度与弹性刚度的比值。LBRB理论骨架曲线示意如图2所示。

图1　LBRB力学模型Fig.1 Mechanical Model of LBRB

受力状态刚度公式钢芯弹性k1=11kw+1kc+1kc钢芯塑性k'1=11αkw+1kc+1kc钢芯塑性钢管弹性k2=11αkw+kt+1kc+1kc

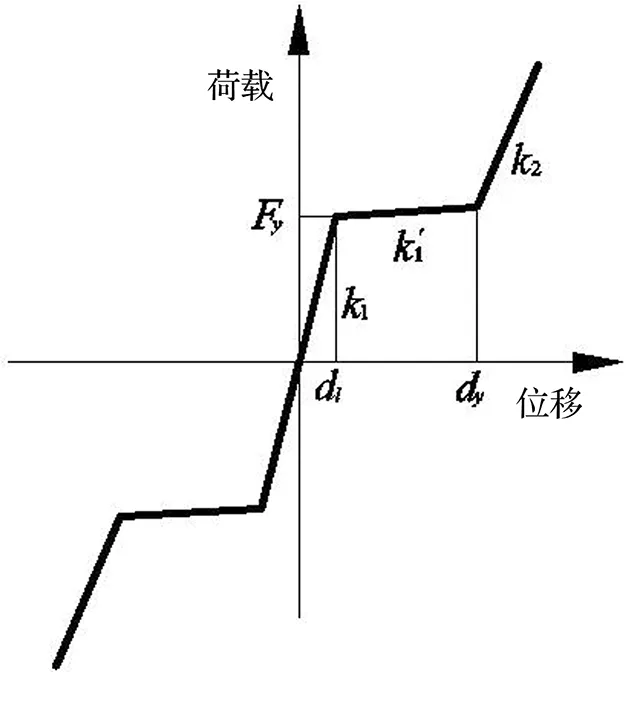
图2　LBRB理论骨架曲线示意图Fig.2 Theoretical skeleton curve of LBRB

2　试验概况

2.1试件设计与参数

LBRB拟静力试验共6根试件，构造图见图3。LBRB试件翼缘板焊接在钢芯两端形成工字形连接段；限位块焊接在过渡段外侧形成钢芯体系。钢板与槽钢(方管)焊接形成中间钢管；两侧焊接挡板及U形槽形成夹持钢管体系。钢芯体系、垫板及两侧夹持钢管体系通过螺栓连接。试件S0及S1～S5组装图分别见图4(a)和(b)。试验主要参数见表2。钢材的主要材性见表3。

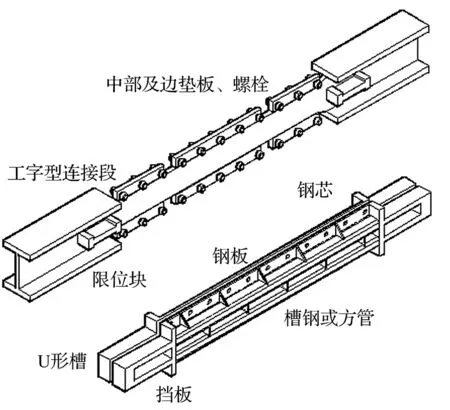
图3　试件构造图Fig.3 Specimen dimensions

编号截面/mm2长度/mm屈服荷载/kN应变(限位距离/mm)间隙S0115×1610185122.5%(25)1S1115×1610185122.5%(25)1S275×1610183352.5%(25)1S3115×165095125%(25)1S4115×165095122.5%(12)1S5115×1610185122.5%(25)2

表2中，试件S0的夹持钢管为钢板焊接槽钢，试件S1～S5的夹持钢管为钢板焊接方管。

试件S1工作段截面对应设计屈服荷载512 kN，设计钢材应变利用率为2.5%；钢芯与夹持钢管之间间隙为1 mm。

试件S2减小工作段截面以考察不同k2/k1的影响，钢芯工作段截面对应设计屈服荷载为335 kN。

试件S3缩短钢芯工作段长度，考察5%钢材应变利用率对LBRB滞回性能的影响。

试件S4钢芯工作段长度同试件S3，但限位距离等比例缩小，与试件S1对比考察对应2.5%钢材应变作为设计限值是否可行。

试件S5在试件S1基础上改变钢芯与夹持钢管之间间隙为2 mm，考察间隙对LBRB承载能力及稳定性的影响。试件主要尺寸及构成见表4，限位块及U形槽截面见图5。

图4　试件组装图Fig.4 Assembly of the specimen

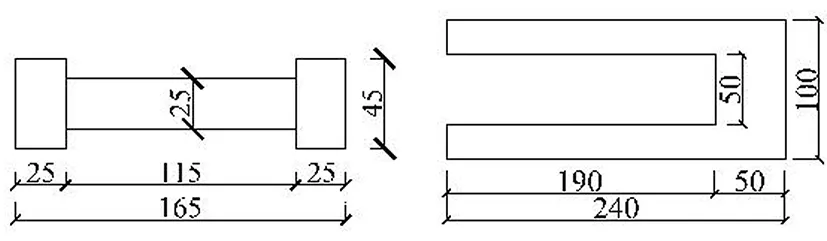
图5　限位块及U形槽Fig.5 displacement stopper and U-shape slot

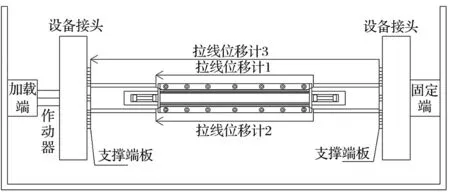
图6　试件加载及位移计布置图Fig.6 Loading facility and displacement gauges placement

型号用途钢号下屈服点/MPa抗拉强度/MPa弹性模量/GPa屈服应变强屈比伸长率/%-16钢芯、挡板Q235278.6443.22040.141.5921.5-8夹持钢管Q235296.5436.52070.21.4729.2[10#夹持钢管Q235285.0474.71870.241.6627.840×40×3夹持钢管Q235439.6523.53000.141.198.8

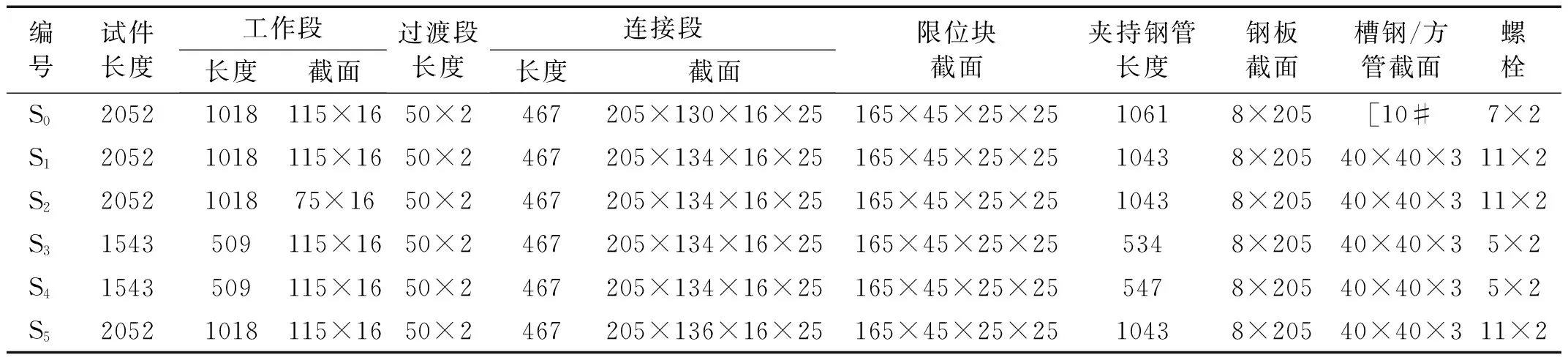
表4　试件主要参数

注：1. 长度单位均为mm，截面单位均为mm2。

2.连接段及限位块截面为工字型。

2.2试验测量及加载方案

拟静力试验采用3 000 kN阻尼器试验系统进行加载，按照图6所示安装构件。

试验过程记录加载轴力和钢芯轴向位移。位移传感器的布置方式如图6所示，位移计1和2所测平均值作为LBRB钢芯轴向变形，位移计3测量LBRB整体轴向变形。

拟静力试验在保证LBRB耗能能力的基础上考察其限位效果。加载全程位移控制，如LBRB设计应变为2.5%时对应限位距离为25 mm，加载以5 mm为幅值增量且每级循环2圈，在25 mm位移附近时减小位移增量以便观察滞回曲线的变化，随后仍以5mm为增量直至构件破坏。加载制度如图7所示。

图7　加载制度Fig.7 Loading system

3　试验结果与分析

3.1试验现象

各试件破坏模式及破坏现象基本相似，多为限位装置发挥作用，荷载大幅提升后发生整体失稳破坏。

试件S0钢芯发生多阶屈曲，螺栓间夹持钢管鼓屈，夹持钢管约束范围内有整体失稳趋势，如图8所示。

图8　试件S0Fig.8 Specimen S0

试件S1在26 mm对应压力荷载下发出金属摩擦声，28 mm对应压力荷载下发出较大声响，35 mm对应压力荷载下有轻响并伴随试件中部压屈，压力荷载接近1 500 kN时发生整体屈曲失稳，如图9所示。

图9　试件S1Fig.9 Specimen S1

试件S2在25 mm对应压力荷载时发出轻微声响，28 mm对应压力荷载下屈曲失稳，如图10所示。

图10　试件S2Fig.10 Specimen S2

试件S3在拉力达到1 400 kN时，钢芯拉断并发出闷响，如图11(a)所示。试验继续测试钢管性能，钢管受拉达到2 200 kN时发生面外弯曲，最终方管与端板焊接处拉裂，如图10(b)所示。

试件S4在15 mm压力荷载下发出轻响，20 mm对应压力荷载下发出钢材摩擦声，最终压屈破坏，如图12所示。

试件S5达到25 mm拉力峰值时，发出尖锐响声，并伴随沙沙的摩擦声，后由于U形槽焊接质量问题，U形槽拉裂破坏，见图13(a)，钢芯所受轴力突然增大，钢芯被拉裂，如图13(b)所示。

图11　试件S3Fig.11 Specimen S3

图12　试件S4Fig.12 Specimen S4

图13　试件S5Fig.13 Specimen S5

3.2试验结果

反复荷载作用下的荷载-位移曲线能够反映防屈曲支撑加载、卸载规律、耗能及滞回规律等。试件S0～S5荷载-位移曲线与理论计算骨架曲线对比详见图14(a)～(f)，图中实线为滞回曲线，虚线为理论骨架曲线。

试件S0～S5滞回环比较饱满，普遍特征是在相应限位距离明显看出附加刚度，说明夹持钢管可以顺利发挥作用，但其值小于设计值，分析原因是S0外约束体螺栓间距过大导致约束不足，夹持钢管发生螺栓间屈曲变形，附加刚度有所折减。受拉状态下由于U形槽与限位块间空隙加工不够精确，造成单侧钢管首先参加工作，由此受拉附加刚度不准确。在后续研究中，为准确考虑钢管刚度的贡献值，需要求较高的试件加工精度以及钢管偏移等导致的刚度折减问题。

下面对破坏现象和滞回曲线中的关键问题逐一进行分析

试件S0，由于连接夹持钢管螺栓间距过大，由于约束不足导致钢管鼓屈，因而附加刚度偏小。拉力及压力荷载下承载能力相近。

试件S1，忽略钢芯的抗弯贡献，假设两端铰接，失稳荷载为3 176 kN，而最终S1破坏形式为中间部分弯曲失稳，分析为钢芯屈服后产生多阶小幅值屈曲变形，夹持钢管两端无约束，只中间与钢芯嵌槽相连，导致钢管受力后与加载轴力并不完全重合，如此产生的初始偏心随荷载的增加逐渐增加，导致构件中间部分发生整体弯曲变形。S2～S5同样存在类似问题。

试件S2，钢芯截面相对S1有所减小，其余条件不变。拉力最大变形值25 mm，拉力最大荷载1 100 kN；压力最大变形达到30 mm，压力最大荷载达到1 600 kN，造成这种现象的原因是钢芯由多阶变形拉直过程中，与夹持钢管之间摩擦力增大，尤其试件中间段产生弯曲的趋势后，这种摩擦力会随之增大。此时，限位空隙加工精度所造成的不良影响会扩大，造成单侧钢管首先受力，从而拉力附加刚度减小。

试件S3，加载至钢芯断裂后继续对夹持钢管轴向加载，滞回曲线分为两部分，将钢管滞回曲线调整到钢芯最终状态，如图14(d)所示，第一次加载阶段，滞回环比较饱满，钢芯的耗能能力良好。第二次加载阶段，受拉承载力主要反映夹持钢管的性能；受压时钢芯断口接触，受压承载力反映夹持钢管与钢芯的性能。夹持钢管上的方形钢管与挡板焊接处拉裂破坏。

试件S4，相对S3其限位距离减小，由荷载位移曲线可知，附加刚度提前实现，与预测相符，说明钢芯应变利用率采用2.5%并保留一定安全储备是可行的。

试件S5，钢芯与夹持钢管之间的间隙由1 mm变为2 mm，由试验滞回曲线可知，承载能力及滞回曲线均具有可靠的稳定性，间隙变化对滞回曲线的影响并不明显，说明1～2 mm的间隙宽度都可保证试件较好实现其性能。

图14　S0～S5滞回曲线Fig.14 Hysteretic Curves of S0～S5

3.3钢芯耗能段恢复力模型

应用Bouc-Wen模型分析6根LBRB试件试验结果中钢芯屈服耗能阶段的滞回性能，如图15(a)～(f)，其中，实线为试验值，虚线为应用Bouc-Wen模型模拟所得拟合值。从曲线可知，Bouc-Wen模型模拟所得滞回结果与试验结果较吻合，说明Bouc-Wen模型可以较好地模拟LBRB的滞回性能。

上述6根试件的相关参数如下表5所示。对于β、γ、n三个决定滞回曲线形状的参数，6根试件参数接近，可近似认为一致且离散性不大，可取平均值进行取值，即β=0.84，γ=0.16，n=1。因此LBRB钢芯耗能段的滞回模型可采用如下公式描述：

RT(u,z)=αku+(1-α)kuyz

另外，k、α、μy等三个参数由支撑构件的几何尺寸及材料特性决定，试验精度达标的基础上可按理论值代入计算并进行分析。屈服后刚度系数均取0.02，刚度值及屈服位移按理论计算结果取值。同时，要考虑加工误差等随机因素的影响。

表5　Bouc-Wen 模型相关参数

4　结　论

(1) 提出一种消能限位防屈曲支撑构件，前期钢芯屈服消耗地震能量，后期夹持钢管提供附加刚度限制过大变形，适用于高层、超高层结构的减震控制。

(2) 拟静力试验结果表明，LBRB钢芯屈服后滞回环饱满，耗能能力良好。应用Bouc-Wen模型模拟消能限位支撑的钢芯耗能阶段滞回性能效果良好，并讨论了相关参数的确定方法。

(3) 附加刚度表现明显，说明夹持钢管能够在加载后期顺利参与受力，但附加刚度确定方法还需进一步研究。

消能限位防屈曲支撑作为一种功能上的创新型支撑，其附加刚度实现程度及构造设计方面还存在不足，需要更多的研究及试验以确定最合理的支撑参数，优化其设计思路，使消能限位防屈曲支撑的研究形成体系。

[1] 汪家铭, 中岛正爱，陆烨. 屈曲约束支撑体系的应用与研究进展(Ⅱ)[J]. 建筑钢结构进展, 2005, 7(2): 1-11.

WANG Jia-ming, NAKASHIMA M, LU Ye． The practice and research development of buckling-restrained braced frames(Ⅱ) [J]. Progress in Steel Building Structures, 2005,7(2):1-11.

[2] 周云. 防屈曲耗能支撑结构设计与应用[M]. 北京:中国建筑工业出版社,2007.

[3] 郝晓燕, 李宏男,牧野俊雄. 装有腹板式钢制防屈曲支撑框架结构振动台试验及分析[J]. 振动与冲击, 2014,33(16): 130-134.

HAO Xiao-yan, LI Hong-nan, TOSHIO Makino. Shaking table experiment and performance analysis of steel frame structure with innovative H type steel-unbuckling-braces[J]. Journal of Vibration and Shock, 2014, 33(16): 130-134.

[4] 张玥, 高向宇, 尹学军, 等. 调谐质量型防屈曲支撑 TMD 构造及动力性能试验研究[J]. 振动与冲击,2014,33(15): 22-30.

ZHANG Yue, GAO Xiang-yu, YIN Xue-jun. Tests for structure and dynamic properties of TMD buckling-restrained braces[J]. Journal of Vibration and Shock, 2014, 33(15): 22-30.

[5] Iwata M, Murai M. Buckling-restrained brace using steel mortar planks; performance evaluation as a hysteretic damper[J]. Earthquake engineering & structural dynamics, 2006, 35(14): 1807-1826.

[6] Black C J, Makris N, Aiken I D. Component testing, seismic evaluation and characterization of buckling-restrained braces[J]. Journal of Structural Engineering,2004,130(6):880-894.

[7] Tsai C S, Lin Y, Chen W, et al. Mathematical modeling and full-scale shaking table tests for multi-curve buckling restrained braces[J]. Earthquake Engineering and Engineering Vibration, 2009, 8(3): 359-371.

[8] 赵俊贤, 吴斌, 欧进萍. 新型全钢防屈曲支撑的拟静力滞回性能试验[J]. 土木工程学报, 2011, 44(4): 60-70.

ZHAO Jun-xian, WU Bin, OU Jin-ping. Uniaxial quasi-static cyclic tests on the hysteretic behavior of a novel type of all steel buckling-restrained brace[J]. China Civil Engineering Journal, 2011,44(4):60-70.

[9] 张振炫，陈清军. 高层建筑结构长周期地震反应的比较研究[J].结构工程师, 2009, 25(4): 78-84.

ZHANG Zhen-xuan, CHEN Qing-jun. A comparative study on long-period seismic responses for high-rise structures[J]. Structural Engineers, 2009, 25(4):78-84.

[10] 廖述清, 裴星洙, 周晓松, 等. 长周期地震动作用下结构的弹塑性地震反应分析[J]. 建筑结构,2005,35(5):24-27.

LIAO Shu-qing, PEI Xing-zhu, ZHOU Xiao-song, et al. Elastic-plastic analysis of earthquake response of structures under the long-period earthquake motion[J]. Building Structure, 2005, 35(5): 24-27.

[11] 韩淼, 周锡元. 基础隔震建筑软碰撞保护分析[J]. 建筑科学, 1999, 15(1): 14-20.

HAN Miao, ZHOU Xi-yuan. Analysis of soft-collision safety for base isolated buildings[J]. Building Science,1999,15(1): 14-20.

[12] 王军文, 李建中, 范立础. 桥梁中抗震限位装置设计方法的研究[J]. 土木工程学报, 2007, 39(11): 90-95.

WANG Jun-wen, LI Jian-zhong, FAN Li-chu. A study on the design method of seismic restrainers for bridges[J]. China Civil Engineering Journal, 2007, 39(11): 90-95.

[13] 闫维波, 李振宝, 马华, 等. 带 RC 耗能器-限位斜撑框架抗震性能研究[J]. 建筑结构, 2009, 38(11): 65-67.

YAN Wei-bo, LI Zhen-bao, MA Hua, et al. Seismic behavior of frame with RC dampers and lock-up braces[J]. Building Structure, 2009, 38(11): 65-67.

[14] 万金国,杨凡,李文峰,等. 双屈服点免断裂屈曲约束支撑性能试验与数值模拟[J]. 建筑结构,2013,17(1):105-108.

WAN Jin-guo, Yang Fan, Li Wen-feng, et al. Experiment research and mechanical simulation of BRB with double yield points and non-fracture[J]. Building Structure,2013,17(1):105-108.

Pseudo-static tests for a new type buckling restrained brace with displacement stopper

MA Hua, ZHANG Fangliang, LIU Yashuang, LI Zhenbao

(Key Lab. of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100024, China)

A new type buckling restrained brace with displacement stopper(LBRB) was proposed here. The energy-dissipation function of a typical buckling restrained brace was performed under smaller deformation and the additional stiffness was provided by the outer restraint element under larger deformation. Thus, the deformation could be limited to a certain level. Pseudo-static tests of 6 LBRB specimens were carried out to investigate the influence of limited distance, working section area, working section length, and clearance between steel core and clamping steel tube on the LBRB’s hysteretic behavior. The results showed that the LBRBs with resonable structures have a good energy-dissipation ability and can provide an additional stiffness under larger deformation.

buckling restrained brace; energy dissipation; displacement stopper; additional stiffness; hysteretic performance

国家自然科学基金项目(51178014)

2015-05-25修改稿收到日期：2015-07-24

马华 女，工学博士，副研究员，1962年生

TU352

A

10.13465/j.cnki.jvs.2016.15.033