基于磁致负刚度装置的低频隔振平台理论设计

张晓平， 何　琳， 周　炜

(1. 海军工程大学 振动与噪声研究所，武汉　430033； 2. 船舶振动噪声重点实验室，武汉　430033)



基于磁致负刚度装置的低频隔振平台理论设计

张晓平1.2， 何琳1.2， 周炜1.2

(1. 海军工程大学 振动与噪声研究所，武汉430033； 2. 船舶振动噪声重点实验室，武汉430033)

基于ANSYS的有限元法开展了三磁体永磁负刚度装置优化设计，采用APDL参数化设计语言，分析了永磁体材料特性及结构参数对负刚度性能的影响。分析表明导磁体能较大程度增强装置负刚度性能；选择剩磁大，矫顽力小的永磁体材料能增强装置的负刚度性能；在体积恒定的情况下，选择大的长宽比以及合适的宽厚比，能获得更大的负刚度性能；装置的初始间隙越小，负刚度性能越强。根据分析结果，采用永磁负刚度装置及钢丝绳隔振器，开展了低频隔振平台的理论设计。

负刚度；永磁体；有限元法；低频；隔振平台

在精密加工、精密测量领域，如MEMS制造、超大规模集成芯片生产、微细电火花加工等对环境振动具有极其严格的要求。超低频、微振动隔振系统[1]能隔离地基和环境微振动对超精密设备的影响，以提供平稳的工作环境。空气弹簧[2-3]以其极低的固有频率及较大的承载能力被广泛应用于精密隔振平台，然而空气弹簧隔振系统复杂，成本高，维护难度大。采用负刚度机构[4-6]与正刚度隔振系统并联，能够降低系统的固有频率，提高隔振系统的隔振性能。Carrella[7]提出使用三个相互吸引的永磁体构建负刚度机构，实验表明系统的固有频率从14 Hz降低到7 Hz。针对质量为3.2 t的圆形微振动平台，选用承载能力大、固有频率较低、蠕变小、寿命长的钢丝绳隔振器作为被动隔振元件，设计适用于该平台的永磁负刚度装置，可降低系统的固有频率至2 Hz以下，具有无需维护、隔振性能优异的优点。

本文采用基于ANSYS的有限元法，分析永磁体材料特性及结构参数对负刚度性能的影响，开展优化设计，为永磁体负刚度装置及低频隔振平台的设计提供依据。

1　永磁负刚度装置原理及有限元分析方法介绍

永磁负刚度装置主要由三块永磁体构成，如图1所示，上下磁体固定与基座，中间磁体连接平台机脚，三块永磁体磁化方向相同，中间磁体同时受上下磁体吸引。由于两块永磁体之间的磁力随间隙呈非线性关系，且间隙越小，吸力越大。

图1　正负刚度并联隔振系统Fig.1 Isolation system with positive and negative stiffness

当中间磁体随平台向下运动时，下磁体对中间磁体的吸力大于上磁体对它的吸力，中间磁体受磁力向下，且位移越大，磁力越大；向上运动时中间磁体磁力向上，且位移越大，磁力越大。由于运动过程中，中间磁体所受磁力与系统恢复力方向相反，该装置具有负刚度特性。

永磁负刚度装置的刚度与永磁体材料、尺寸、磁体之间的间隙、导磁结构等因素有关，永磁体磁力的理论分析[8-9]非常复杂，而实验研究[10]成本高、耗时长。

基于ANSYS的有限元计算方法能够快速、准确地研究各参数对负刚度的影响。永磁负刚度装置采用了三块方形永磁体，采用三维静态磁场标量法对其进行参数化建模及仿真分析。装置关于XZ、YZ两个面对称，为降低计算量，建模时仅截取装置的四分之一，采用四面体单元、自由网格划分方式对所有体进行单元划分，有限元模型如图2所示。

图2　永磁负刚度装置有限元模型Fig. 2 Finite element model of PMNSD

给中间磁体施加力标志。采用FMAGSUM对中间磁体上的虚功力求和。本文运用APDL提供的循环控制语句*DO、*ENDDO在自动修改参数后重复执行命令流。计算不同永磁体材料、尺寸、间隙条件下中间磁体的磁力随位移的变化，并对磁力与位移的曲线进行拟合，得到永磁负刚度装置在平衡位置的动刚度。

2　永磁负刚度装置刚度影响因素分析

2.1刚度随位移变化的特性分析

永磁体磁力与磁体间距离呈强烈的非线性关系，文献[11]采用了四次多项式对两磁体间磁力进行了拟合，而磁致负刚度装置的中间磁体所受磁力可表示为

(1)

式中:a，b为永磁负刚度装置的磁力系数。由此可得到永磁负刚度装置的刚度为：

K=-a-bx2

(2)

可见，永磁负刚度装置的刚度与位移成二次方的非线性关系。

表1　 刚度随位移变化特性分析计算条件

根据表1的参数，计算永磁负刚度装置在大位移变化(±8 mm)的情况下中间磁体磁力与位移的关系，如图3所示。

图3　大位移条件下的磁力-位移曲线Fig.3 Magnetic force-displacement curve under large displacement

图中可以看到中间磁体磁力与位移呈一定的非线性关系，采用三次多项式对曲线进行拟合，得到

F=-1.57-410.33x+0.0145x2-1.06x3

(3)

根据式(1)及式(2)，对式(3)作一定的近似，舍去小量——常数项及二次项，得到系数

a=410.33,b=0.35

(4)

由于刚度表达式中二次项系数很小，刚度非线性并不是特别明显。另外，精密仪器设备工作过程中位移在1 mm以内，同样采用表1中的参数，计算得到永磁负刚度装置在小位移(±2 mm)变化条件下的刚度系数为

a=417.16,b=0.037

(5)

可见，二次项系数非常小，可以忽略不计。因此可以将永磁负刚度装置在±2 mm位移范围内的刚度近似为线性的，其刚度值采用的仿真曲线拟合得到。

2.2导磁体对刚度的影响

按照表2中的参数进行计算。在自由空间中，永磁体的磁场将填充整个临近的空间区域，如图4所示，如不采取任何导磁措施，永磁体负刚度装置对外辐射强烈的磁场，严重影响系统其他部件。

表2　导磁体影响计算参数

图4　无导磁体的磁场分布Fig.4 Magnetic field without magnetizer

在永磁体上、下、左、右四个面采用厚度为20 mm的纯铁制作一个封闭的环，构成封闭的磁路，分析表明，永磁体外的磁场基本上沿着导磁体通过，仅有极少量漏磁，如图5所示。

图5　无导磁体的磁场分布Fig.5 Magnetic field with magnetizer

另外，计算发现加装导磁体后，则装置刚度由-192.8 N/mm变为-454.4 N/mm，如图6所示。分析认为，导磁体构成了一条封闭的磁路，几乎没有漏磁和损耗，磁体间气隙的磁通量最大化，因此中间磁体受的磁力也是最大化的，装置负刚度特性得到明显增强。

图6　磁力-位移曲线(有、无导磁体对比) Fig.6 Magnetic force-displacement curve with or without magnetizer

2.3永磁体材料属性对刚度的影响

永磁体材料属性主要包含剩磁感应强度Br和矫顽力Hcb，采用APDL三层嵌套循环，按照表3的参数，计算了不同Br和Hcb时的刚度。

表3　材料属性影响计算条件

图7　材料属性对装置刚度的影响Fig.7 Effect of material properties on device’s stiffness

从图7可以看出，剩磁对刚度的影响非常大，以Hcb=1 000 kA/m为例，当剩磁Br从1 T增加到1.5 T，永磁负刚度装置的刚度由-194 N/mm变到-454 N/mm。装置负刚度特性随剩磁增强而增强。

矫顽力对刚度的影响较小，以Br=1.25 T为例，当矫顽力Hcb从800 kA/m增加到1 200 kA/m，装置刚度由-316.2 N/mm变到-304.7 N/mm。装置负刚度特性随矫顽力增大而减弱。

因此，为增强装置的负刚度特性，应尽量选择剩磁大，矫顽力小的永磁体材料。

2.4永磁体结构长宽比对刚度的影响

通常，永磁体体积越大，磁力也越大，装置的负刚度也越强。但是相同体积下永磁体的结构尺寸对刚度也有一定的影响。定义永磁体长宽比λ=L/W，在永磁体体积恒定的条件下，保持面积S=LW及厚度H恒定，按照表4的参数，计算不同λ情况下装置的刚度，结果见图8。

表4　长宽比影响计算条件

图8　长宽比对装置刚度的影响Fig.8 Effect of λ on device’s stiffness

可以看到，刚度曲线并非关于λ=1对称，且在λ≈1/2附近具有极大值(受结构参数的影响，极大值位置会发生变化)，在λ小于极大值段，随着λ增加，装置刚度增加，负刚度特性减弱；在λ大于极大值段，随着λ增加，装置刚度减小，负刚度特性增强，且增幅较大。

这是由于导磁体位于L×H面的侧边，当λ减小，永磁体宽度W增加，长度L减小，则导磁体的截面积L×HL减小，导磁体中产生了磁饱和现象，装置中的漏磁严重，影响了刚度；而当λ增大，导磁体的截面积大，不会产生磁饱和，磁路上漏磁越小，充分发挥了永磁体的磁力。

因此，为增强装置的负刚度特性，在永磁体体积恒定、厚度恒定的情况下，应选择矩形截面，且应尽量选择较大的长宽比。同时应保证导磁体平行于长边，以增大导磁体截面积。

2.5永磁体宽厚比对刚度的影响

定义永磁体宽厚比α=W/H，永磁体体积保持恒定，且L=W，按照表5的参数，计算不同α情况下装置的刚度，结果见图9。

表5　宽厚比影响计算条件

图9　宽厚比对装置刚度的影响Fig.9 Effect of α on device’s stiffness

从计算结果可以看到，随着宽厚比增大，装置的刚度呈先显著减小，后缓慢地减小，在α≈3.4附近取得极小值(受结构参数的影响，极小值位置会发生变化)，然后随α增加，刚度又缓慢增加。因此，在设计永磁体结构时，若限定了永磁体的体积，则应优先考虑增大感应面积。但是，一方面，由于永磁体材料较脆，若厚度太小，结构强度不足；另一方面，若一味地增大宽厚比，装置的负刚度特性反而会减弱，因此应当根据计算合理地选择宽厚比。

2.6初始间隙对刚度的影响

由于永磁体之间的吸力与磁体间的间隙呈强烈的非线性关系，永磁负刚度装置的初始间隙对刚度具有较大的影响。图10计算出了初始间隙3 mm～10 mm条件下装置的刚度，可以看到，随着间隙增加，装置负刚度特性迅速减弱。

表6　初始间隙影响计算条件

图10　初始间隙对装置刚度的影响Fig.10 Effect of initial gap on device’s stiffness

因此，在满足平台正常工作的运动位移范围条件下，应尽量使用小的初始间隙，以充分发挥装置的负刚度特性。

2.7综合分析

通过以上对有无导磁体、永磁体材料属性、长宽比、宽厚比、初始间隙等对永磁负刚度装置的刚度的影响分析，综合各方面因素，得到以下几条设计准则：

(1) 设计具有足够截面积的导磁体，使永磁负刚度装置形成一条最佳的封闭磁路，尽可能减小漏磁，一方面可以增强负刚度性能，另一方面还能控制永磁负刚度装置对其外部设备的磁场影响；

(2) 尽可能选用剩磁大，矫顽力相对较小的永磁体材料；

(3) 根据永磁体负刚度装置的外形尺寸限制，将永磁体设计为长方形，长宽比取1～4；

(4) 充分利用尺寸空间，使永磁体的感应面积最大，其次尽可能增大厚度，厚度一般不超过宽边长度；

(5) 结合永磁负刚度装置的应用场合，确定工作位移及极限位移，将永磁负刚度装置的最小初始间隙设为比极限位移大1～2 mm。

(6) 根据被动隔振系统刚度，确定所需要的负刚度的大小，通过调节永磁体结构尺寸以及初始间隙，设计负刚度合适的永磁负刚度装置。

3　低频隔振平台设计

3.1系统设计

低频隔振平台总质量为3.2 T，选用四个HGGS-800型钢丝绳隔振器进行支撑，并联四只永磁负刚度装置，结构如图11所示。

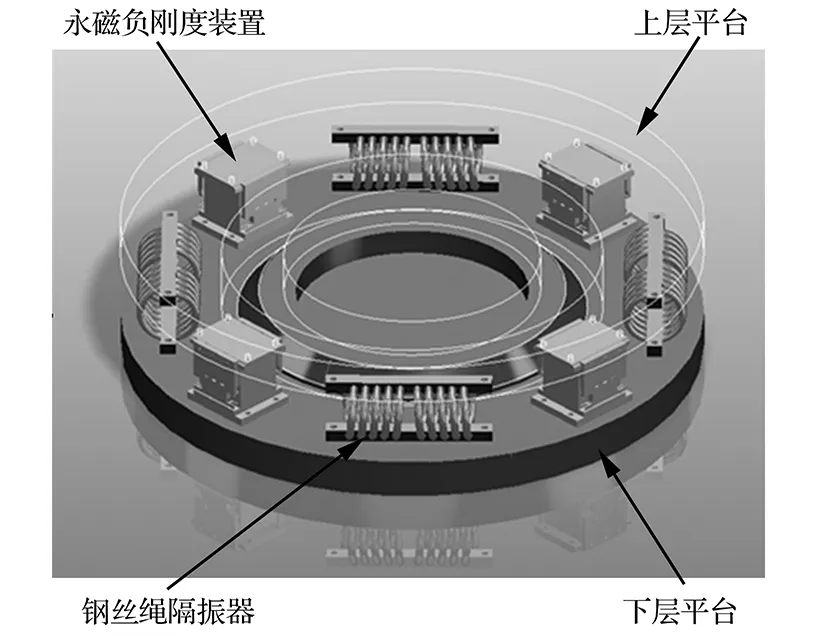
图11　低频隔振平台结构示意图Fig.11 Diagram of low frequency vibration isolation platform

平台安装时，首先采用四个钢丝绳隔振器支撑上层平台，并在上层平台上安放好精密仪器设备，让钢丝绳隔振器稳定工作在静平衡位置。将永磁负刚度装置的中间磁体调整到上下磁体的正中央，即平衡位置，并锁定，然后将其安装到下层平台中间，并采用垫片调整其与上层平台之间的间隙，最后解除永磁负刚度装置锁定，使上层平台可以在一定范围内上下运动。由于永磁负刚度装置的中间磁体位于平衡位置，并不会产生对外的力，上层平台始终保持在原来的静平衡位置，即未改变平台的静刚度。永磁负刚度装置能够抵消钢丝绳隔振器的正刚度，降低了平台的动刚度。

3.2系统固有频率设计

额定载荷下动刚度为980 N/mm，根据固有频率常规计算公式：

为降低平台的固有频率到2 Hz以下，要求单个负刚度装置的刚度为：

选用某厂家一种性能优异的永磁材料，其剩磁Br=1.39 T，矫顽力Hcb=1 011 kA/m。隔振平台正常工作情况下运动位移范围限制在±1 mm以内，因此设置负刚度装置初始间隙为2 mm。受结构尺寸限制及结构强度要求，长宽均小于200 mm，选择长宽比约为2～4，在平行长边的方向上设置导磁体，厚度为15 mm～30 mm以内。按照表7、表8、表9中的永磁体长、宽、导磁体厚度参数进行相关计算。

从计算结果可以看到，当厚度为15 mm时，满足刚度需求的最小永磁体尺寸为200 mm×100 mm×15 mm，体积为300 cm2；当厚度为20 mm时，满足刚度需求的最小永磁体尺寸为200 mm×60 mm×20 mm，体积为240 cm2；当厚度为25 mm时，满足刚度需求的最小永磁体尺寸为200 mm×50 mm×25 mm，体积为250 cm2。同时考虑到永磁体材料非常脆，为保证装置强度，厚度不宜太小。又若永磁负刚度装置负刚度过强，系统的刚度过于低，会导致系统抗干扰能力弱。因此，经综合考虑，最终选择宽度为永磁体尺寸为200 mm×60 mm×20 mm。此时，隔振平台系统的固有频率为：

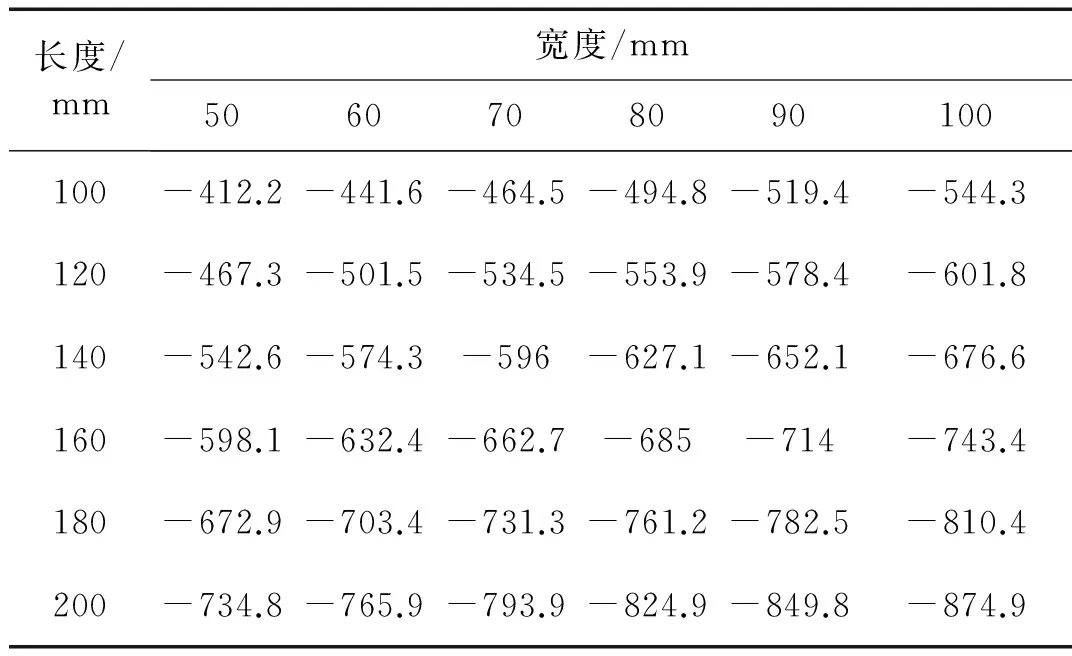
表7　永磁负刚度装置刚度计算(厚度15 mm)

表8　永磁负刚度装置刚度计算(厚度20 mm)

表9　永磁负刚度装置刚度计算(厚度25 mm)

3.3系统动力学特性分析

由于低频隔振平台主要是用于隔离环境微振动对精密仪器设备的影响，上层平台在工作中产生的位移极其微小，可以忽略钢丝绳隔振器及永磁负刚度装置的非线性影响，将钢丝绳隔振器简化为刚度元件及阻尼元件，将永磁负刚度装置简化为负刚度元件。

低频隔振平台属于积极隔振系统，下层平台至上层平台之间的位移传递率为：

(6)

当系统不并联永磁负刚度装置时，

k=4×980 000=39 200 000

c=4×200=800

(7)

当系统并联永磁负刚度装置时，

k=4×(980 000-878 400)=406 400

c=4×200=800

(8)

将式(7)、式(8)分别带入式(6)中，可得到并联永磁负刚度装置后系统的隔振性能曲线，如图12所示。可见，永磁负刚度装置能够显著提高隔振系统的低频隔振效果，并联永磁负刚度装置后，100 Hz以下频带的宽频隔振效果提高了6.3 dB。

图12　低频隔振系统位移传递率Fig.12 Displacement transmissibility oflow frequency vibration isolation platform

4　结　论

永磁负刚度装置采用三块永磁体产生负刚度特性，与具有正刚度的钢丝绳隔振器并联使用，可降低系统的固有频率，提高隔振平台的低频隔振效果。本文采用ANSYS的APDL参数化设计语言，分析了永磁体材料特性及结构参数对永磁体负刚度装置负刚度性能的影响，分析表明：① 导磁体能较大程度增强装置负刚度性能；② 选择剩磁大，矫顽力小的永磁体材料能增强装置的负刚度性能；③ 在体积恒定的情况下，选择大的长宽比以及大的宽厚比，能获得更强的负刚度性能；(4)装置的初始间隙越小，负刚度性能越强。最后，针对3.2 t重的微振动平台，通过计算选择合适的永磁体尺寸，设计出的永磁负刚度装置能使低频隔振平台的固有频率达到1.79 Hz，使用永磁负刚度装置后平台的隔振效果提高了6.3 dB。

[1] 陈智锋，张绍宗，吕海宝，等．隔振设计在超精密加工与测量中的应用[J]．航空精密制造技术，2002，38(3)：10-13.CHEN Zhi-feng, ZHANG Shao-zong, LÜ Hai-bao, et al. The application of design of vibration insulation in ultra precision machining and measuring[J]. Aviation Precision Manufacturing Technology,2002,38(3):10-13, 31.

[2] 罗奇．大型超低频空气弹簧隔振平台电磁阻尼系统相关研究[D]．哈尔滨:哈尔滨工业大学，2006.

[3] 赵建文．空气弹簧在光学平台隔振系统中的应用研究[D]．西安:西安电子科技大学，2006.

[4] 纪晗，熊世树，袁涌，等．基于负刚度原理的结构减震效果理论分析[J]．振动与冲击，2010，29(3)：91-94.

JI Han, XIONG Shi-shu, YUAN Yong, et al. Influence analysis of the structural seismic reduction effect based on negative stiffness principle[J].Journal of Vibration and Shock, 2010, 29(3): 91-94.

[5] 纪晗，熊世树，袁涌．基于负刚度原理的结构隔震效果分析[J]．华中科技大学学报:自然科学版，2010，38(2)：76-79.

JI Han, XIONG Shi-shu, YUAN Yong. Analyzing vibration isolation effect of structures using negative stiffness principle[J]. Journal of Huazhong University of Science & Technology:Natural Science Edition,2010, 38(2): 76-79.

[6] 路纯红，白鸿柏．新型超低频非线性被动隔振系统的设计[J]．振动与冲击，2011，30(1)：234-236.

LU Chun-hong, BAI Hong-bai. A new type nonlinear ultra-low frequency passive vibration isolation system[J]. Journal of Vibration and Shock, 2011, 30(1):234-236.

[7] Carrella A，Brennan M J，Waters T P， et al．On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J]．Journal of Sound and Vibration, 2008, 315:712-720.

[8] 田录林，杨小萍，李言，等．适用于永磁轨道及永磁轴承的解析磁力模型的研究[J]．摩擦学报，2008，28(1)：33-73.

TIAN Lu-lin, YANG Xao-ping, LI Yan, et al. Analytical magnetic force model for permanent magnetic guide way and permanent magnetic bearings[J].Tribology, 2008, 28(1):33-73.

[9] Ebrahimi B, Khamesee M B, Golnaraghi M F. Design and modeling of a magnetic shock absorber based on eddy current amping effect[J]. Journal of Sound and Vibration, 2008,(315): 875-889.

[10] 李强，徐登峰，范新，等．新型永磁隔振器的隔振性能分析与实验研究[J]．振动与冲击，2013，32(13)：6-11．

LI Qiang, XU Deng-feng, FAN Xin, et al. Analysis and test of vibration isolation performance for a novel permanent magnet vibration isolator[J]. Journal of Vibration and Shock, 2013, 32(13): 6-11.

[11] 谢佳君，高学绪，包小倩. 永磁体磁力与永磁隔振系统固有频率分析[J].磁性材料及器件，2011，42(2)：17-19.

XIE Jia-jun, GAO Xue-xu, BAO Xiao-qian. Analysis of magnetic force between cylinder magnet pair(s) and natural frequency of vibration isolation system based on them[J]. Journal of Magnetic Materials and Devices,2011, 42(2)：17-19.

Theoretical design of a low frequency vibration isolation platform based on permanent magnet negative-stiffness device

ZHANG Xiaoping1,2, HE Lin1,2, ZHOU Wei1,2

(1.National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China;2. Institute of Noise and Vibration, Naval University of Engineering, Wuhan 430033, China)

Theoretical design of permanent magnet negative-stiffness devices(PMNSDs) was developed with the finite element software ANSYS. The effects of magnet material characteristics and structural parameters on their negative-stiffness performance were analyzed using APDL. The results showed that the devices’ negative-stiffness performance can be improved by using magnetizers and the magnet material with higher remanence and lower coercivity, the larger ratio of length to width, the appropriate ratio of width to thickness, and the devices’ clearance as small as possible. Based on the above study results, the theoretical design of a low frequency vibration isolation platform using PMNSDs and wire-rope isolators was developed.

negative stiffness; permanent magnets; finite element method; low frequency; vibration isolation platform

新世纪优秀人才支持计划

2015-05-07修改稿收到日期：2015-08-05

张晓平 男，博士生，1986年10月生

何琳 男，教授，博士生导师，1957年11月生

TU317

A

10.13465/j.cnki.jvs.2016.15.031