基于物料运动特性的旋回破碎机生产率分析

李　强　巩亚东　宋伟刚

东北大学，沈阳，110819



基于物料运动特性的旋回破碎机生产率分析

李强巩亚东宋伟刚

东北大学，沈阳，110819

为研究旋回破碎机动锥低速运转状态下对散体物料的破碎性能并改善破碎腔型，结合物料在破碎腔内的运动和力学特性，提出了破碎机生产率计算方法。从分层破碎原理出发，基于破碎腔几何结构，研究物料在排料和挤压半周期的运动形式，并对运动轨迹进行绘制；再根据物料在阻塞层的上拱速度和排料速度对生产率进行求解，并以PXF6089旋回破碎机为算例，进行离散元方法和实际生产验证。仿真及物理实验证明该计算方法可行。

旋回破碎机; 运动特性; 生产率; 离散元方法

0　引言

在煤炭矿山、建筑建材等工业部门，为提高燃料燃烧效率或对矿物有用成分进行解离，需对原矿进行碎磨加工。目前，已出现基于电、热、磁、声等的多种新型破碎方法，但基于经济性考虑，各选矿企业仍以机械破碎为主，其中旋回破碎机可完成岩石粗中碎。

为提高企业经济效益，需对旋回破碎机生产性能进行深入研究，提高产品生产率。而散体物料通过破碎腔的运动方式直接影响破碎机生产效率，所以需建立物料流动方程并研究物料运动轨迹。国内外已有学者在破碎机生产性能方面开展相关研究。文献[1-4]提出了分层破碎原理，并采用选择函数、破碎函数和分级函数建立矩阵模型对破碎机破碎性能进行预测。

文献[5-8]结合Evertsson的研究成果，提出了圆锥破碎机生产率建模新方法，并以此为主目标对破碎腔型进行多目标参数优化，根据该理论制成物理样机，破碎性能显著提高。Atta等[9]以物料流动模型和破碎产品粒度模型为理论基础，通过控制闭边排料口尺寸和动锥转速来提高破碎机生产性能。

目前对破碎机生产率的研究大多基于细碎圆锥式破碎机，该类型破碎机衬板与岩石之间作用力及压缩比较小，为实现生产性能优化，需提高动锥旋摆速度以实现物料在排料半周期的自由落体运动。而中粗碎旋回破碎机破碎比较大，破碎过程中岩石对衬板作用力大，若采用较高的旋摆速度易加速衬板磨损，会降低破碎机使用寿命。所以散体物料在旋回破碎机与圆锥破碎机破碎腔中流动模型不同，以滑动形式为主，物料受力复杂。虽然Evertsson等[2]基于牛顿运动定律和加速度合成定理对散体物料流动模型进行了深入研究，但该模型过于复杂，解析解求解困难，故需在保证生产率理论解与实际生产结果相符的前提下，对物料流动模型进行简化处理或重新建立物料在腔体中的流动模型。

本文在充分研究旋回破碎机动锥低速运动状态下破碎腔中散体物料在排料和挤压半周期的流动特性，并忽略如小摆角造成的曲线运动等运动学次要因素，提出了建立物料流动模型及旋回破碎机生产率模型的新方法。以PXF6089旋回破碎机为算例，通过离散元仿真方法和实际生产数据对模型准确性进行验证。

1　散体物料在破碎腔中的运动形式

物料在破碎腔中的运动形式主要取决于动锥转速及动锥在给料口和排料口的摆动行程。物料运动主要存在三种形式：沿动锥衬板和物料群滑动、自由落体运动以及自由落体和滑动并存[8]。

根据Evertsson的研究，在实际工况下，将物料运动形式发生转变的两个极限转速定义为n1和n2。若动锥旋摆速度小于n1，物料发生纯滑动运动；若动锥旋摆速度大于n2，物料将发生自由落体运动；若转速介于n1和n2之间，当物料靠近给料口时，发生滑动运动，而在排料口附近将发生自由落体运动[8]，即

(1)

(2)

式中，S1、S2分别为动锥在入料口和排料口的摆动行程；t1、t2分别为物料发生自由落体运动和滑动运动的临界时间；αB为动锥底角。

2　旋回破碎机物料运动轨迹

2.1PXF6089破碎机破碎腔结构参数分析

PXF6089旋回破碎机动锥衬板母线由多段相互连接的直线段构成，但各直线段斜率差别不大。为便于研究，将动锥衬板母线阻塞点以上部分在以悬挂点为原点、竖直方向为y轴的绝对坐标系下进行一元线性回归拟合，取母线上各线段的端点为拟合点，得到动锥母线在挤压半周期极限位置的直线方程：

y=5.251x+2117

(3)

相似度R2=0.9942，该拟合直线的斜率K1=5.251，倾斜角αB=79.2177°。PXF6089旋回破碎机在给料口、排料口动锥摆动行程分别为S1=8mm，S2=44mm，可计算出物料发生纯滑动的临界转速n2=137r/min，而该型号破碎机推荐动锥摆速n=120r/min，因此，物料在破碎腔的运动为纯滑动形式。

2.2挤压半周期物料运动轨迹

当物料破碎过程趋于稳定时，挤压半周期内破碎腔中物料严密压实，无向下流动趋势，其运动形式由动锥转速决定。当动锥转速小于滑动临界转速时，物料沿其他物料群或衬板发生纯滑动运动，且两种运动形式及受力状态相似。

取第i破碎层靠近动锥衬板某物料质点为研究对象，为便于观察物料运动形式，对动锥摆动行程适当放大，如图1所示。

图1　挤压半周期物料运动轨迹

挤压半周期内物料运动形式为以悬挂点O为圆心、物料质心到悬挂点距离Ri为矢径的单摆运动，该运动最大摆角γ为动锥进动角的两倍，则物料摆动轨迹为弧线ABC，而国内外生产的旋回破碎机进动角大多小于0.5°，因此，可将物料运动轨迹近似成一条直线AD，摆动行程li为

li=Riγ

(4)

设物料在第i破碎层排料口极限位置A点的坐标为(xA，yA),则物料质点到悬挂点O的矢径Ri及物料运动轨迹AD方程分别为

(5)

(6)

设该轨迹终点坐标为D(xD，yD),根据两点之间距离公式及矢径摆动行程，可得D点坐标为(xA-γyA，yA+γxA)，则物料在挤压半周期运动轨迹可唯一确定。

将该破碎层物料的运动速度在全局坐标系下进行分解，水平方向运动使物料发生挤压破碎，竖直方向运动使物料上拱，物料上拱速度为

(7)

其中，ω为物料质点在纵截面上单摆摆动速度，该参数与物料运动时间t、动锥旋摆角速度ωn及进动角γ相关，即

ω=ωnγsinωnt

(8)

设ξ为矢径和动锥母线之间的夹角，根据两直线夹角定理，该参数与矢径斜率K2和动锥母线斜率K1相关，即

(9)

2.3排料半周期物料运动轨迹

取第i个破碎层靠近动锥衬板某物料质点为研究对象，如图2所示。

图2　排料半周期物料运动轨迹

以物料质心为原点，以衬板母线方向为y轴建立相对坐标系x′o′y′。相对坐标系在全局坐标系下最大摆角γ=0.012rad，忽略动锥的摆动，则相对坐标系只发生平移运动，运动形式为沿动锥衬板或其他物料群滑动运动和垂直于矢径Ri匀速直线运动的合成，将这两个运动在相对坐标系下进行正交分解，设起点A坐标为(xA，yA)，则物料在第i个破碎层的运动轨迹为

(10)

则排料半周期第i个破碎层物料在全局坐标系的运动轨迹方程为

(11)

若散料可破碎，且在破碎过程中满足充分平稳给料，忽略动锥自转和物料切向运动的影响。根据式(5)～式(11)，在MATLAB环境下对PXF6089旋回破碎机破碎腔物料运动轨迹进行绘制，如图3所示。

图3　PXF6089旋回破碎机物料运动轨迹

3　PXF6089旋回破碎机生产率建模

破碎机生产率的研究大多基于物料在破碎腔内自由落体运动而开展，未考虑当动锥转速过低时，物料的滑动运动状态。为了对PXF6089旋回破碎机性能进行预测和优化，需对其生产率进行理论建模。

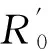
图4　破碎机阻塞层横截面结构参数

根据物料运动特性，在排料半周期内，物料运动可在全局坐标系下分解为沿竖直和水平两个方向的运动。在竖直方向上位移可表示为f(t)，对其进行一阶求导，可表示在t时刻物料运动速度。

图4中A点所对应的是挤压半周期的极限位置，C点为排料半周期的极限位置，物料在A、C点的速度分别与破碎层纵截面中物料在每一破碎层的滑动起点和终点速度相等，且图4中速度基于α的分布与纵截面中速度基于时间的分布是相同的。因此，物料在阻塞层的排料速度为

(12)

同理，物料在排料半周期阻塞层C点和D点的速度与阻塞层纵截面起点和终点的速度相等，且阻塞层基于α的速度分布与基于时间的速度分布相同，则物料在阻塞层的上拱速度为

(13)

结合余弦定理，则物料在阻塞层的排料量和上拱量分别为

(14)

(15)

4　PXF6089生产率模型离散元验证

4.1矿石物料物性参数标定

为保证理论模型的准确性和有效性，需对以PXF6089旋回破碎机为算例的生产率模型进行验证。根据破碎机在低速状态下的生产率模型及PXF6089旋回破碎机推荐几何结构和运动参数(表1)，设物料在破碎腔的松散密度为1.6 t/m3。则可计算其理论生产率Q=3997.44 t/h。

表1　PXF6089旋回破碎机运动学和结构特性

近年来，随着对高精度、高复杂度破碎过程模型的需求，一些计算机软件(如EDEM)被广泛采纳并应用于破碎领域，取得了很好的效果[10-13]。由于破碎过程模型的建立主要依赖于岩石本构参数，而目前对该参数的研究多从黏结颗粒模型(bonded particle model，BPM)着手[14-17]，采用夹逼处理的方法，以岩石的宏观力学特性为指标进行微观参数标定[18]。对PXF6089旋回破碎机常规处理的铁矿石进行BPM平行键参数标定，具体标定参数及其他散体物料物性参数见表2。

表2　岩矿物料物性参数

4.2基于EDEM旋回破碎机工作过程仿真

根据某选矿企业提供的矿石物料粒度分布形式，对给料岩矿进行离散化处理，并采用模具挤压的方法按照实际矿石形态建立矿石模型。对PXF6089旋回破碎机进行结构和运动建模并简化处理，其工作过程的仿真主要包括三个阶段：颗粒物料替换、平行键生成及物料破碎。选择数据记录时间间隔为0.01 s，仿真时间为25 s，计算机实际工作时间为123 h，文件大小为70 GB。图5所示为不同时刻物料破碎仿真过程。

(a)t=0.4 s(b)t=4.6 s

(c)t=9 s(d)t=13 s图5　PXF6089旋回破碎机工作过程仿真

4.3仿真结果分析

在EDEM后处理模块中，建立质量传感器，可记录PXF6089旋回破碎机破碎产量，如图6所示。

图6　PXF6089旋回破碎机产量

从图6可看出，在2 s前破碎机产量较少，此时物料刚下落，未填满破碎腔；物料填满破碎腔后，物料破碎产量直线上升，破碎均匀；14 s后物料破碎基本完成，产量增加趋于平缓。

为计算破碎机瞬时生产率，需提取离散元中数据，并进行相应处理，如图7所示。从图7可看出，在2 s前，岩矿未填满破碎腔，随矿石物料逐渐下落，破碎机生产率直线上升。在4 s时，瞬时生产率达到3400 t/h。在6 s到12 s内，物料在破碎机满载工作状态下进行破碎，可看出此过程破碎机生产率为3700 t/h，且存在波动，但基本稳定在3500～4000 t/h之间。在12 s后，瞬时生产率急剧下降，破碎腔内物料减少，破碎效率降低。

图7　PXF6089旋回破碎机瞬时生产率

5　PXF6089生产率现场测量

为验证生产率理论公式计算的可靠性，还需对某选矿厂旋回破碎机生产率进行现场测量，该选矿厂选用一台PXF6089旋回破碎机作为粗碎设备。完成物料卸载、挤压破碎和产量的记录，如图8所示。为记录实际生产率，选矿厂采用在输送带托辊下方安装称重传感器(即皮带秤)的方式实时监控并记录产量。经过近一年的记录，在排矿口调整为170 mm情况下，实际测量PXF6089旋回破碎机生产率为3500～4000 t/h。

(a)物料卸载(b)物料破碎起始

(c)物料破碎终止(d)产量记录图8　PXF6089旋回破碎机工作过程

将PXF6089旋回破碎机生产率理论计算值、离散元仿真值和现场测量数据汇总，见表3。

表3　PXF6089旋回破碎机生产率汇总　t/h

从表3可看出，计算、仿真和现场测量数据趋于一致，但理论值偏大，因为当物料在排料半周期从挤压极限位置向排料极限位置运动的过程中，矢径发生变化，而理论计算所代入矢径为最大值，因此，理论生产率偏大，但该数值仍在仿真和现场测量可行参数域中，证明生产率计算模型可行。

6　结论

(1)基于层压破碎原理，对物料在挤压和排料半周期运动特性进行研究，并利用MATLAB对物料通过破碎腔运动轨迹进行绘制。

(2)基于物料和破碎机运动学特性及物料在破碎腔受力特性，建立低速旋回破碎机生产率理论模型。

(3)以PXF6089旋回破碎机为算例，进行离散元仿真和实际生产验证，所得生产率理论计算值在仿真和现场测量数据参数域中，但由于对计算方法进行简化，造成理论值偏大，故该值可作为PXF6089的最大生产率。

[1]Evertsson C M，Bearman R A. Investigation Interparticle Breakage as Applied to Cone Crushing[J]. Minerals Engineering，1997，10(2)：199-214.

[2]Evertsson C M.Modelling of Flow in Cone Crushers[J]. Minerals Engineering，1999，12(12)：1479-1499.

[3]Evertsson C M. Output Prediction of Cone Crushers[J]. Minerals Engineering，1998，11(3)：215-231.

[4]Lindqvist M，Evertsson C M. Improved Flow and Pressure Model for Cone Crushers[J]. Minerals Engineering，2004，17(11/12):1217-1225.

[5]Huang Dongming， Fan Xiumin，Wu Dianliang，et al.Multi-objective Planning of Cone Crusher Chamber，Output and Size Reduction[J].Minerals Engin-eering，2009，22(12)：1091-1093.

[6]Dong Gang，Huang Dongming,Fan Xiumin. Cone Crusher Chamber Optimization Using Multiple Constraints[J].International Journal of Mineral Processing，2009，93(2)：204-208.

[7]Dong Gang，Fan Xiumin，Huang Dongming. Analysis and Optimization of Cone Crusher Performance[J].Minerals Engineering，2009，22(12): 1091-1093.

[8]黄东明.挤压类破碎机工作机理和工作性能优化研究[D].上海：上海交通大学，2007.

[9]Atta K T, Johansson A, Gustafsson T. Control Oriented Modeling of Flow and Size Distribution in Cone Crushers[J].Minerals Engineering, 2014, 56(2):81-90.

[10]Weerasekara N S，Powell M S，Cleary P W，et al. The Contribution of DEM to the Science of Comminution[J]. Powder Technology，2013，248(248)：3-24.

[11]Lichter J, Lim K, Potapov A, et al. New Developments in Cone Crusher Performance Optimization[J].Minerals Engineering,2009, 22(7):613-617.

[12]Quist J.Cone Crusher Modeling and Simulation-development of a Virtual Rock Crushing Enviro-nment Based on the Discrete Element Method with Industrial Scale Experiments for Validation[R]. Göteborg: Chalmers University of Technology, 2012.

[13]Morrison R D，Shi F，Whyte R. Modeling of Incremental Rock Breakage by Impact-for Use in DEM Models[J]. Minerals Engineering，2007，20(3)：303-309.

[14]Potyondya D O，Cundall P A. A Bonded-particle Model for Rock[J]. International Journal of Rock Mechanics & Mining Sciences，2004，41(8)：1329-1364.

[15]Ding Xiaobing，Zhang Lianyang.A New Contact Model to Improve the Simulated Ratio of Unconfined Compressive Strength to Tensile Strength in Bonded Particle Models[J]. International Journal of Rock Mechanics & Mining Sciences，2014，69：111-119.

[16]Manouchehrian A，Sharifzadeh M，Marji M F，et al. A Bonded Particle Model for Analysis of the Flaw Orientation Effect on Crack Propagation Mechanism in Brittle Materials under Compression[J].Archives of Civil and Mechanical Engineering，2014，14(1)：40-52.

[17]Obermayr M, Dressler K, Vrettos C, et al. A Bonded-particle Model for Cemented Sand[J]. Computers & Geotechnics, 2013, 49(49):299-313.

[18]Quist J.Cone Crusher Modelling and Simulation[D].Nybro:Chalmers University of Technology，2012.

(编辑陈勇)

Gyratory Crusher Productivity Analysis Based on Kinematic Characteristics of Materials

Li QiangGong YadongSong Weigang

Northeastern University,Shenyang,110819

For investigating the bulk material breakage performance of gyratory crusher under the low speed of mantle and improving the structure of crushing chamber, combining with the kinematic and dynamic characteristics of materials,a calculation method of productivity was proposed. On the basis of Layered breakage theory and the structure of crushing chamber, the bulk material motion forms of discharge and compressive half cycle were researched and the trajectories were draw. Productivity was solved based on the materials velocity of upward and downward in the choke layer. Numerical results of PXF6089 gyratory crusher were presented. The data of actual production and discrete element method were adopted to verify the results accuracy. Simulation results and physical experimental results show the calculation method is accurate.

gyratory crusher; kinematic characteristics; productivity; discrete element method (DEM)

2015-09-30

TD451

10.3969/j.issn.1004-132X.2016.15.008

李强，男，1986年生。东北大学机械工程与自动化学院博士研究生。主要研究方向为矿山机械。巩亚东，男，1958年生。东北大学机械工程与自动化学院教授、博士研究生导师。宋伟刚，男，1963年生。东北大学机械工程与自动化学院教授、博士。