旋转尺蠖压电电机驱动机构自由振动分析

邢继春　张　楠　李　冲

燕山大学，秦皇岛，066004



旋转尺蠖压电电机驱动机构自由振动分析

邢继春张楠李冲

燕山大学，秦皇岛，066004

提出了一种新型旋转尺蠖压电电机。考虑旋转尺蠖压电电机驱动机构为连续系统，建立了驱动机构动力学模型；利用该动力学模型求解了样机驱动机构的固有频率和模态函数。分析了系统参数对驱动机构固有频率的影响规律，为旋转尺蠖压电电机的设计打下了理论基础。

旋转尺蠖；驱动机构；模态分析；压电电机

0　引言

近年来，利用尺蠖运动原理的压电高精密微位移驱动器逐渐应用于精密测量、微机电系统、精密加工装配、纳米科学仪器、生物细胞操纵和半导体装备等领域[1]。压电精密驱动器根据输出的运动形式分为直线型和旋转型[2]，根据驱动信号的频率可分为准静态驱动器和超声驱动器。准静态驱动器驱动信号频率较低，常见的有尺蠖压电电机、惯性冲击式压电电机等[3]。驱动信号频率较高的超声驱动器中关于行波超声电机研究的文献较多，成果也较为突出[4]。而且，现有的旋转型压电电机中行波超声电机最为常见，其特点为输出速度较高、行程较大，但在高精密定位中其定位精度和分辨率较低[5]。而准静态压电电机中的尺蠖压电电机则能将大行程与高精度、高分辨率很好地兼容，并且克服了惯性冲击式压电电机输出力矩较小的缺点[6]。

目前，尺蠖压电电机设计研究的类型多为直线型驱动器，将尺蠖驱动机理应用到精密旋转驱动技术中的实例不多[7]，并且该种电机的传动系统的驱动与控制理论尚不完善，因此，大大限制了尺蠖电机在微动精密控制领域中的应用[8-9]。本文提出了一种新型旋转尺蠖压电微动电机。该电机以压电叠堆作为驱动元件，由于定子的特殊结构，当工作时驱动机构可产生角度位移；并且具有实现箝位装置可调、单个零件结构简单、能够实现微动压电电机大行程等优点。本文针对旋转尺蠖压电电机的关键部件驱动机构建立动力学模型，并进行自由振动分析。

1　旋转选尺蠖压电机工作原理

图1　旋转尺蠖压电电机

图1为旋转尺蠖压电电机实物图及爆炸图。时序驱动信号如图2所示，图2中A为驱动电压幅值，T为电机工作一个周期的时间。当施加图2a所示的时序信号时，图3中压电叠堆1伸长，钳位机构3顶住转子。继续输入图2b所示时序信号，压电叠堆5伸长，由于驱动机构利用杠杆位移放大原理，驱动机构7发生弯曲。钳位机构3带动转子9顺时针转过一定角度θ。当输入图2c所示时序信号时，压电叠堆2伸长顶住转子后，撤销压电叠堆1和5的电压信号，钳位机构3和驱动机构7恢复原状。钳位机构4带动转子转过角度θ。将压电叠堆6输入图2d所示的时序信号后，压电叠堆6伸长，驱动机构8发生弯曲，钳位机构4再带动转子顺时针转过角度θ。撤销压电叠堆2和6的电压信号，钳位机构4和驱动机构8恢复原状。完成了一个周期的动作。重复上一周期的动作，以此来实现完整的连续运动。

(a)压电叠堆1　　　　　　(b)压电叠堆2

(c)压电叠堆3　　　　　　(d)压电叠堆4图2　时序驱动信号

图3　驱动原理示意图

2　驱动机构动力学模型的建立

如图4所示，驱动机构由基座和驱动机构两部分固连组成，并通过基座上的中心孔与固定轴形成过盈配合，其中1为压电堆，2为支撑梁，3为驱动梁，4为基座梁。建立驱动机构动力学模型，对驱动机构进行相应的简化。驱动机构关于x轴、y轴成反对称结构，因此，取驱动机构的1/4进行动力学问题研究，并作以下假设：

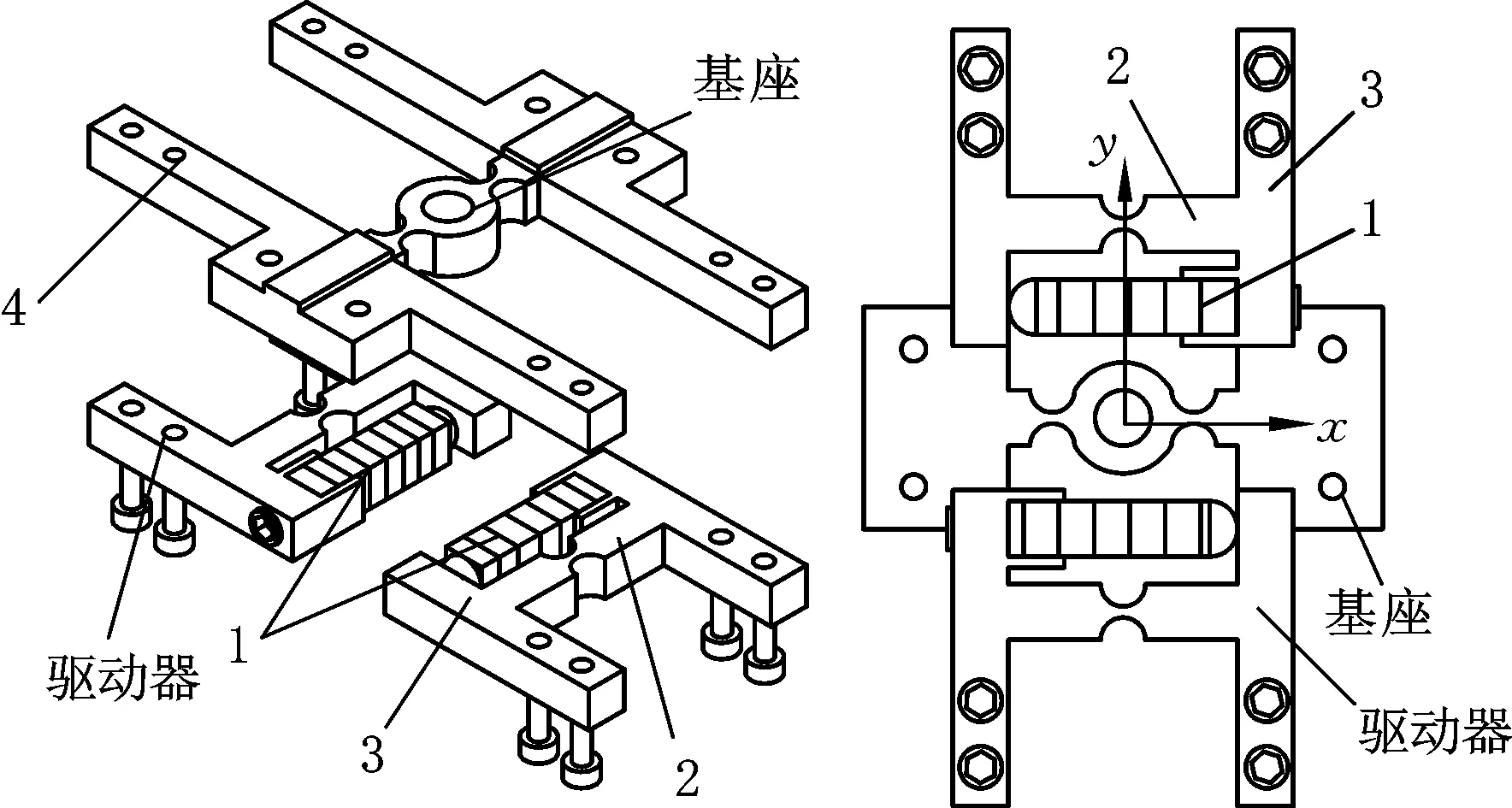
图4　驱动机构轴测爆炸图和驱动机构平面图

(1)考虑驱动机构的弹性变形主要发生在压电叠堆、支撑梁、驱动梁和基座梁上。

(2)考虑支撑梁的长度小于截面高度的5倍，该梁段为铁摩辛柯梁，故考虑截面剪切惯量和转动惯量。

(3)考虑支撑梁和基座梁处两尺寸相同的柔性铰链弯曲变形，忽略拉伸变形，将柔性铰链视为铰链与卷簧的组合，卷簧刚度为K，可利用直圆型柔性铰链转动刚度公式[7]求解：

s=R/t

式中，Mz为关于z轴的弯矩；αz为关于z轴的转角；E为驱动机构材料弹性模量；hj为铰链宽度；t为凹口处最小厚度；R为切口半径。

(4)驱动梁与基座梁通过两个螺钉固连。考虑两梁在两螺钉位置l5、l6处有相同的动态位移，如图5所示。

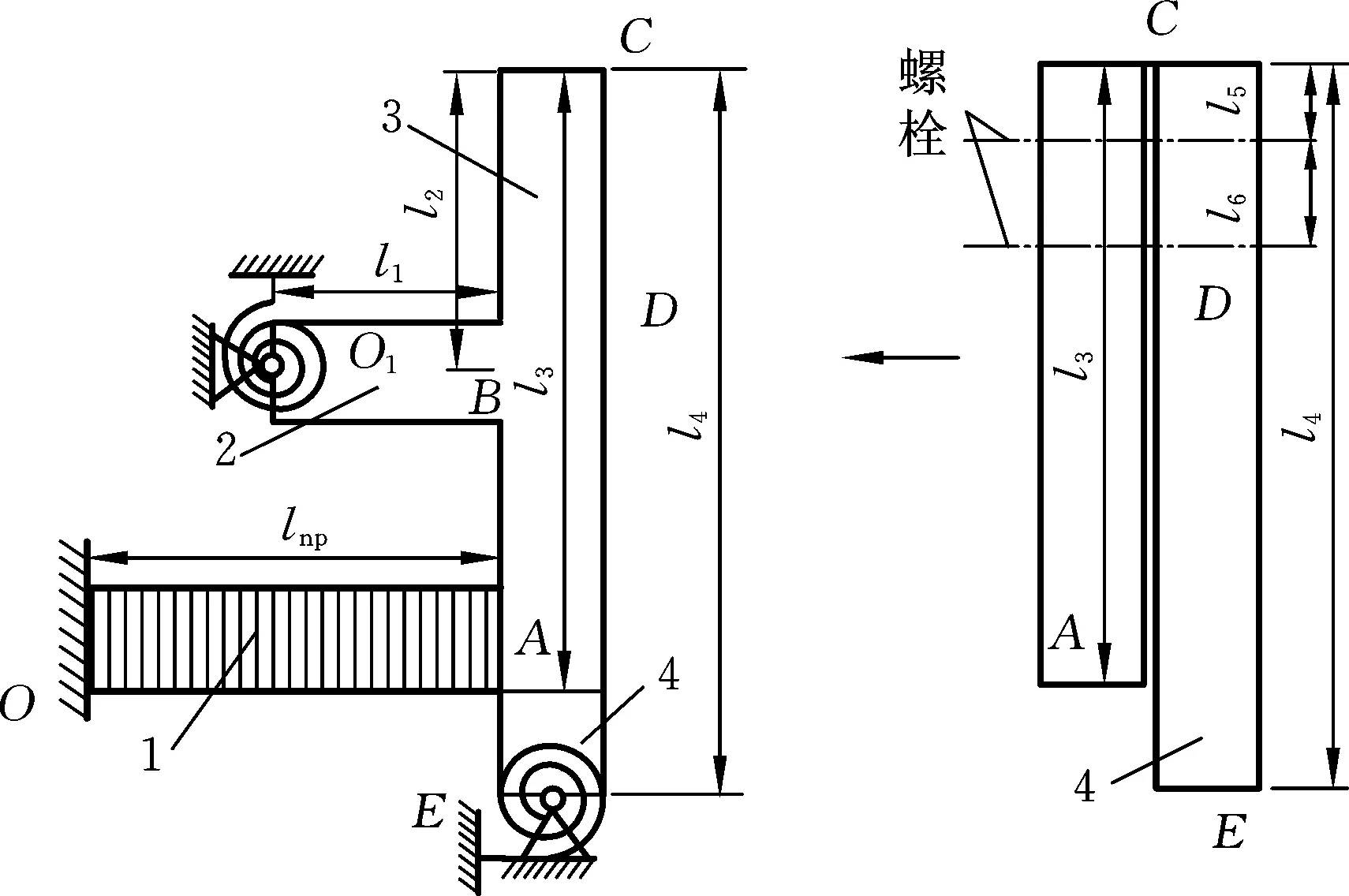
图5　驱动机构简化模型图

2.1压电堆自由振动

压电叠堆为多层压电陶瓷片的粘合体。考虑压电叠堆为连续系统，忽略层与层间的能量耗损，预紧力不能使压电堆产生电荷，忽略预紧力对动力学模型的影响，只考虑压电叠堆纵向振动。

(1)

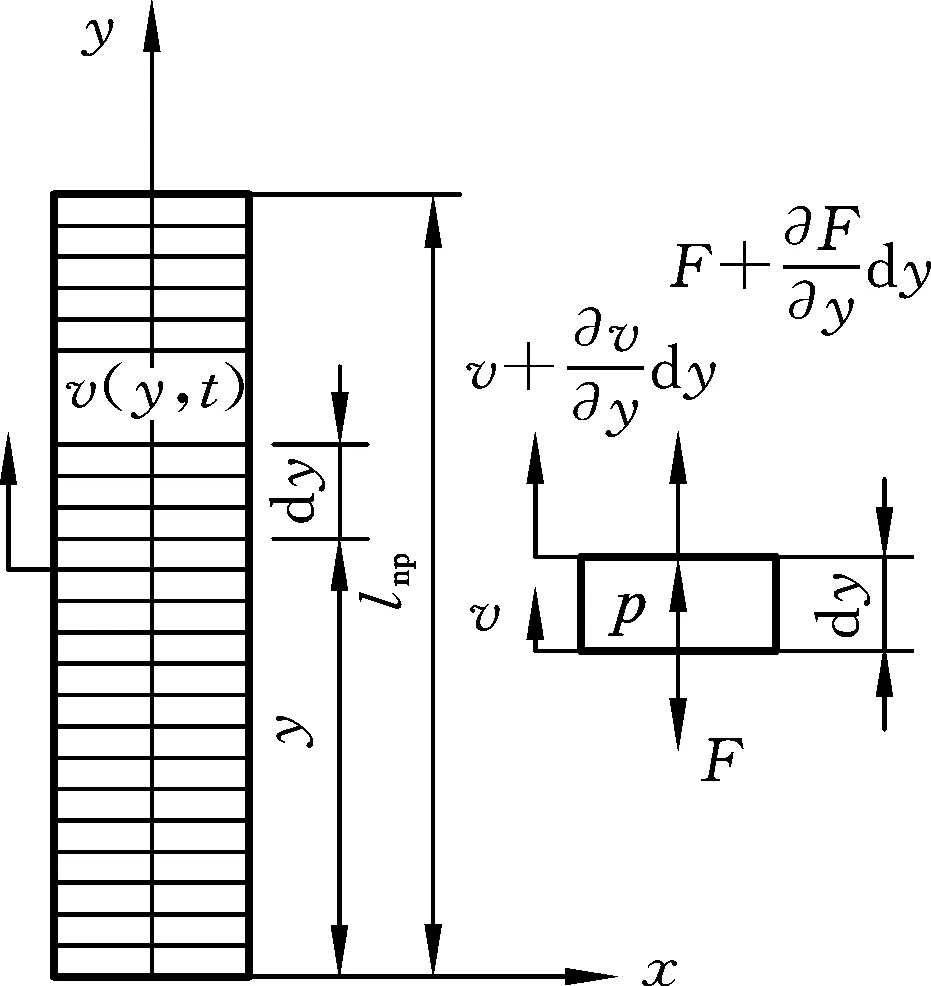
图6　压电堆动力学模型

由压电本构方程推导出轴向内力表达式：

(2)

其中，d33为压电系数，当驱动电压信号V(t)=0时，把式(2)代入式(1)，令p=0，得到压电堆轴向振动偏微分方程：

(3)

设式(3)解的形式为

v(y,t)=φp(y)q(t)

(4)

其中，q(t)为广义坐标，压电堆轴向振动模态φp(y)为

(5)

系数Ai(i=1,2)由边界条件确定，进而得出无穷多个固有频率ωi(i=1,2,…)及对应的模态函数φpi(i=1,2,…)。

2.2支撑梁自由振动

简化支撑梁，其动力学模型如图7所示，考虑支撑梁的长度小于截面高度的5倍，认为该梁为铁摩辛柯梁模型，O1端柔性铰链简化为简支端和定刚度卷簧，刚度为K。对支撑梁模型建立坐标系，对应的弯曲振动横向位移为y1(x1,t)，梁的密度和弹性模量分别为ρ、E,横截面积为S1，极惯性矩为I1，作用在梁上的分布载荷为f(x1,t)。

图7　支撑梁动力学模型

设梁的切变模量为G，取厚度dx1为研究对象，截面产生的切应变γ=Fs/(κGS1)，Fs为单元所受剪力，κ为截面形状因素。截面因刚体转动产生的角度θ和应变γ都使中心轴的切线偏转，则有∂y1/∂x1=θ+γ。

对微元应用牛顿第二定律列出平衡方程：

f(x1,t)dx1

(6)

令式(6)中f=0，代入切应变，化简可得

(7)

考虑截面转动产生的惯性力矩，建立力矩平衡方程：

(8)

其中，M为单元所受弯矩；J为截面转动惯量，J=ρI1。

由力矩和转角的关系知M=-EI1∂θ/∂x1，代入式(8)，化简整理得

(9)

从式(7)、式(9)中消去θ，可得铁摩辛柯梁动力学方程：

(10)

仅考虑转动惯量的影响，忽略剪切变形，式(10)可简化为

(11)

设式(11)中解的形式为

y1(x1,t)=φ(x1)q(t)

(12)

其中，φ(x1)为支撑梁的模态函数。代入式(11)得

(13)

(14)

(15)

设式(15)解的一般形式为

φ(x1)=eλx1

(16)

将式(16)代入式(15)，导出本征方程为

λ4+δ2λ2-β4=0

(17)

解出4个本征值：±iβ1，±β2，其中

则式(15)的通解，即支撑梁的模态函数为

φ(x1)=B1cos(β1x1)+B2sin(β1x1)+

B3sinh(β2x1)+B4cosh(β2x1)

其中，系数Bi(i=1,2,3,4)可由边界条件确定，并可得到无穷多个固有频率ωi(i=1,2,…)及对应的模态函数φi(i=1,2,…)。

2.3驱动梁和基座梁自由振动

驱动梁和基座梁动长度均大于截面宽度的5倍，可视为欧拉-伯努利梁。两个梁左端分别在长度为l5、l6处利用螺栓固连，驱动梁右端与压电堆相连，基座梁右端利用柔性铰链约束。其动力学模型如图8所示。

图8　驱动梁和基座梁动力学模型

在驱动梁中，取微元dx2为研究对象，建立动力学方程：

(19)

以右截面上任一点为矩心建立平衡方程：

(20)

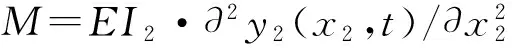
(21)

设式(21)中方程解的形式为

y2(x2,t)=η(x2)q(t)

(22)

将式(22)代入式(21)导出

η(4)(x2)-β2η(x2)=0

(23)

则式(23)的通解，即驱动梁的模态函数为

η(x2)=C1cos(βx2)+C2sin(βx2)+

C3sinh(βx2)+C4cosh(βx2)

其中，系数Ci(i=1,2,3,4)可由边界条件确定，从而可以得到无穷多个固有频率ωi(i=1,2,…)及对应的模态函数ηi(i=1,2,…)。

在基座梁中，取dx3单元体为研究对象，微元体沿y3方向的动力学方程为

(25)

微元体满足力矩平衡条件，力矩平衡方程为

(26)

上述方程与驱动梁动力学方程一致，故可得简化后的弯曲振动方程：

(27)

将式(27)的解分离变量，把解的形式写成

y3(x3,t)=ψ(y)q(t)

(28)

将式(28)代入式(27)，导出

ψ(4)(x3)-β4ψ(4)(x3)=0

(29)

式(29)的通解，即基座梁的模态函数为

ψ(x3)=D1cos(βx3)+D2sin(βx3)+

D3sinh(βx3)+D4cosh(βx3)

通过边界条件可确定式(30)中系数Di(i=1,2,3,4)，进而得到固有频率ωi(i=1,2,…)及对应的模态函数φi(i=1,2,…)。

2.4边界条件和连续条件

由驱动机构分离后各段的边界条件和连续条件，可知以下关系式：

(1)压电堆y=0处为固定端，此处轴向位移为零，即

φp(0)=0

(31)

(2)支撑梁x1=0处为卷簧和铰链，挠度为零，转角不为零，即

(32)

(3)驱动梁x2=0和基座梁x3=0处为自由端，弯矩和剪力均为零，即

(33)

(4)基座梁x3=l4处为弹性约束，边界条件为

(34)

(5)压电堆y=lnp和驱动梁x2=l3结合处，有

(35)

(6)支撑梁x1=l1和驱动梁x2=l2结合处，有

(36)

(7)驱动梁与基座梁通过螺栓固连，螺栓位置在l5、l6处，有

(37)

3　结果分析

3.1固有频率及模态分析

驱动机构结构参数见表1，将参数代入连续条件得出系统的固有频率及振型，不同材料对应的固有频率见表2。图9～图11所示为前3阶固有频率对应的振型，且振型图中标出了l5、l6及l2位置处的位移值。

表1　结构参数

表2　不同材料对应的固有频率　rad/s

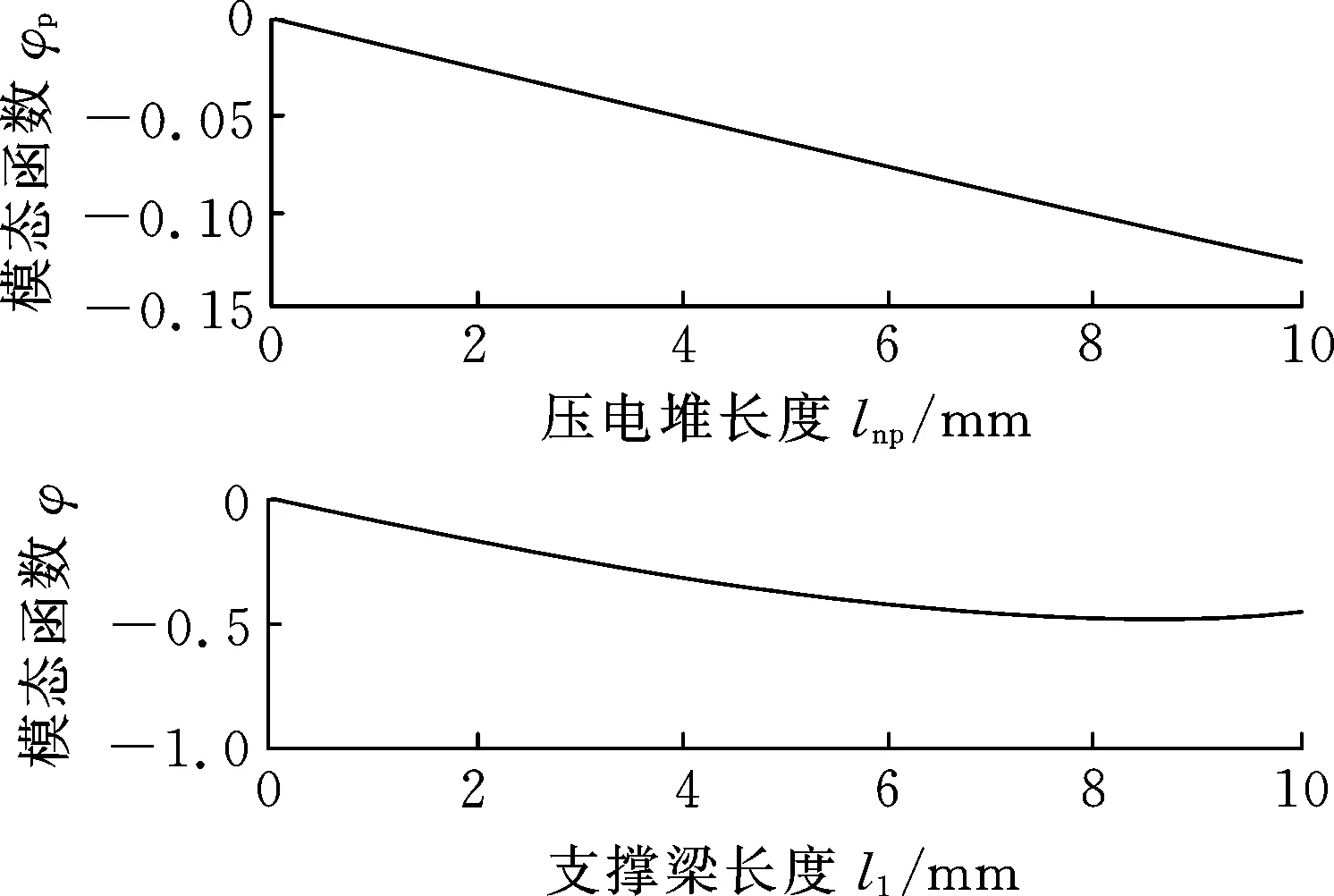
(a)压电堆和支撑梁振型

(b)驱动梁和基座梁振型图9　驱动机构1阶振型

由表2和图9～图11可知：

(1)在5种材料中，黄铜对应的驱动机构同阶固有频率最小，碳钢对应的同阶固有频率最大。不同材料对应的固有频率中，2阶和3阶固有频率总是相差最小。

(2)同阶振型中，压电堆的轴向振动和支撑梁对应的铁摩辛柯梁的弯曲振动较弱，而驱动梁和基座梁对应的欧拉伯努利梁的弯曲振动现象较明显。这是因为压电堆和支撑梁都是截面与长度尺寸比值较大而不易产生振动。

(a)压电堆和支撑梁振型

(b)驱动梁和基座梁振型图10　驱动机构2阶振型

(a) 压电堆和支撑梁振型

(b)驱动梁和基座梁振型图11　驱动机构3阶振型

(3)同阶固有频率中，驱动梁和基座的l5和l6处的位移值分别相同，这与l5和l6处因螺栓连接而具有相同位移的假设是一致的。

3.2系统参数对结构的影响规律

分别选取梁高度h(包括h1、h3、h4)，铰链宽度hj，各梁段长度l1、l3、l4及螺栓作用位置l5为目标参数，作固有频率随参数变化曲线，如图12～图17所示，可知：

图12　固有频率随h变化情况

图13　固有频率随hj变化情况

图14　固有频率随l1变化情况

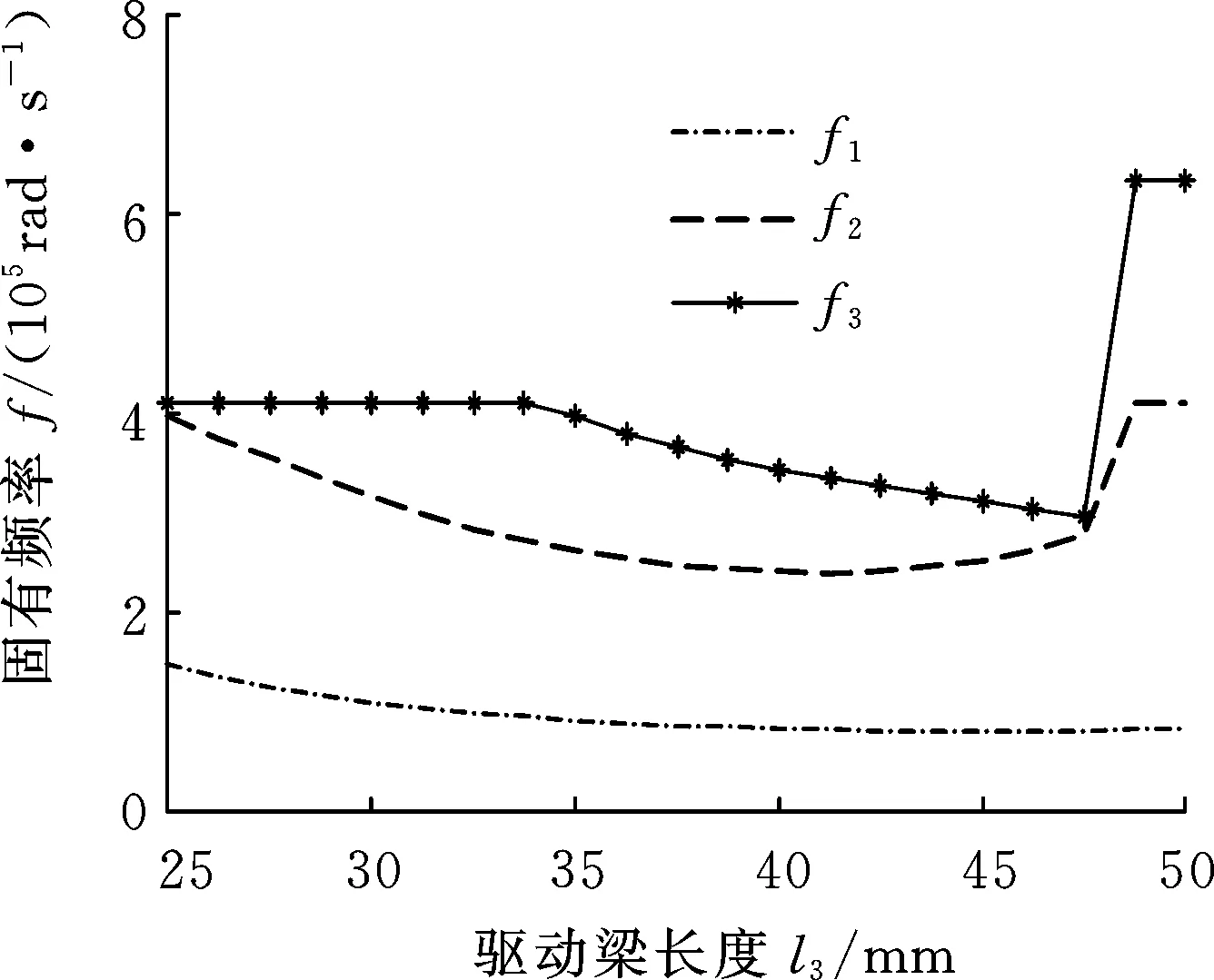
图15　固有频率随l3变化情况

图16　固有频率随l4变化情况

图17　固有频率随l5变化情况

(1)随h的增大，1阶固有频率f1先增大后减小，2阶和3阶固有频率f2、f3先增大而后趋于平稳。这是由于当梁高度h较小时，各梁段皆已振动，随梁高度的增大固有频率增大；当梁高度h继续增大时，铰链相对各梁段更易发生振动，故系统的固有频率变化不大。

(2)随铰链宽度hj的增大，1阶和2阶固有频率不变，3阶固有频率先增大后不变。

(3)随l1的变化，固有频率基本没有发生变化，这是由于支撑梁是铁摩辛柯梁，其主振动频率远大于驱动梁和基座梁的主振动频率，故支撑梁长度的改变对驱动机构低阶固有频率的改变影响很小。

(4)随l3的变化，2阶和3阶固有频率变化较大，且固有频率值在3阶固有频率时出现了突变，这是由于l3对驱动梁会产生直接影响，且驱动梁相对容易振动，故较低频率容易随l3发生变化，并且随l3的增大到某一值使得振型发生变化。

(5)l4变化时，1阶和2阶固有频率发生局部变化，而3阶固有频率没有发生变化，这是由于基座梁相对于驱动梁更加容易振动，故其主振动频率是最低的。

(6)当l5增大并且l6与l5相对距离不变时，2阶和3阶固有频率在某一区间先不变后减小，而1阶和2阶频率都不变。

4　结论

(1)选用碳钢材料可以增大驱动机构的固有频率。

(2)驱动梁和基座梁的振动比压电堆和支撑梁的振动显著。

(3)参数h、l3对驱动机构系统总体固有频率的影响较大。

(4)理论分析为新型旋转尺蠖压电电机的样机改进和实验研究打下了理论基础。

[1]Richard J C.Nano-scale Measurements and Manipulation [J]. Journal of Vacuum Science and Technology: B, 2004, 22(4): 1609-1635.

[2]Duong K, Garcia E.Design and Performance of a Rotary Motor Driven by Piezoelectric Stack Actuators[J].Japanese Journal of Applied Physics,1996,35：6334-6341.

[3]Itatsu Y, Torii A, Ueda A.Inchworm Type Microrobot Using Friction Force Control Mechanisms[C]//2011 International Symposium on Micro-nano Mechatronics and Human Science (MHS). Nagoya, 2011:273-278.

[4]赵淳生. 世界超声电机技术的新进展[J].振动、测试与诊断，2004，24(1):1-5.

Zhao Chunsheng. Recent Progress in Ultrasonic Motor Technique[J].Journal of Vibration,Measur-ement& Diagnosis,2004,24(1):1-5.

[5]Bernard Y,Christen J L,Hernandez C,et al.From Piezoelectric Actuator to Piezomotor[J].Piers Online,2001,7(5):416-420.

[6]Sun Xiantao, Chen Weihai, Zhang Jianbin, et al. A New Novel Piezo-driven Linear-rotary Inchworm Actuator[J]. Sensors and Actuators A:Physical,2015, 224:78-86.

[7]Li Jianping，Zhao Hongwei，Shao Mingkun，et al．Design and Experiment Performance of an Inchworm Type Rotary Actuator[J].Review of Scientific Instruments,2014,85: 085004.

[8]Tomoyuki Y， Ryuichi Y，Masashi I，et al.Applica-tion of Micro Piezo Actuator (SIDM)—Lens Drive for Mobile Phone Camera[J].Journal of the Japan Society for Precision Engineering,2009,75(1):144-145.

[9]Kihwan K,Nahmgyoo C,Woojin J.The Design and Characterization of a Piezo-driven Inchworm Linear Motor with a Reduction Mechansim[J].JSME International Journal, Series C: Mechanical Systems, Machine Elements and Manufacturing,2004,47(3):803-811.

(编辑陈勇)

Free Vibration Analysis of Driving Mechanisms of a Rotary Inchworm Piezoelectric Motor

Xing JichunZhang NanLi Chong

Yanshan University，Qinhuangdao，Hebei，066004

A novel rotary inchworm piezoelectric motor was proposed herein. Considering the driving mechanism of the rotary inchworm piezoelectric motor was a continuous system, the dynamics model of the driving system was presented. The natural frequencies and mode function of the drive mechanism of a prototype were solved by using the dynamics model. The influences of system parameters on the natural frequency of the driving mechanism were analyzed. All the conclusions lay a theoretical foundation for the design of the rotary inchworm piezoelectric motors.

rotary inchworm；driving mechanism；modal analysis；piezoelectric motor

2015-11-16

燕山大学青年教师自主研究计划课题资助项目(13LGB002)

TH113.1DOI：10.3969/j.issn.1004-132X.2016.15.002

邢继春，男，1983年生。燕山大学机械工程学院讲师。主要研究方向为压电电机驱动与控制。发表论文10余篇。张楠(通信作者)，男，1981年生。燕山大学机械工程学院副教授。李冲，男，1988年生。燕山大学机械工程学院博士研究生。