柔性臂杆、柔性关节空间机械臂T-S模糊轨迹跟踪及双柔振动并行综合控制

洪昭斌　　 陈　力　　李文望

1. 厦门理工学院，厦门，361024　　2. 福州大学，福州，350108



柔性臂杆、柔性关节空间机械臂T-S模糊轨迹跟踪及双柔振动并行综合控制

洪昭斌1陈力2李文望1

1. 厦门理工学院，厦门，3610242. 福州大学，福州，350108

针对存在参数不确定和外界干扰的柔性臂杆、柔性关节空间机械臂追踪期望运动的问题，设计了基于T-S模糊模型的滑模鲁棒控制方案和双柔性振动并行控制方案。首先，设计了关节柔性补偿器以提高系统的等效关节刚度。其次，利用反馈线性化技术建立了系统追踪期望轨迹的误差动力学方程，通过对系统Lyapunov稳定性证明来选择滑模控制参数；简化并改进T-S模糊推理规则，提出了模糊滑模鲁棒控制方法，可解决滑模控制的抖振问题并具有计算量少、控制力矩小的优点。再次，提出了柔性臂杆振动模态的直接反馈控制方案，解决了双柔性并行综合控制的问题。最后，运用逐步仿真的方法，对比仿真结果，证实了所设计轨迹跟踪、双柔性并行综合控制方案的有效性和稳定性。

空间机械臂；柔性臂杆-柔性关节；参数不确定；T-S模糊滑模控制；双柔性并行控制

0　引言

空间机器人[1-3]可代替宇航员进行太空试验、探测、操作等活动，对空间机器人进行动力学分析、控制等研究是各国太空计划的重点领域。为了减小空间机器人的质量，其机械臂杆件大多设计为轻质的细长柔性杆[4-6]，这样的柔性杆通常具有较大的尺寸并产生低频的大幅值柔性振动，系统刚柔耦合效应严重。同时，在使用电机驱动机械臂杆时，由于制造技术、齿轮及减速器的弹性等原因，驱动关节也呈现柔性[7]的性质并产生弹性振动。因此，在针对空间机器人进行动力学分析、控制时，同时考虑其关节柔性、臂杆柔性对控制性能的影响具有非常重要的意义。然而，以上研究或者仅考虑了柔性关节对空间机器人轨迹跟踪精度的影响，或者仅解决了柔性杆振动模态的控制问题，同时解决关节柔性、臂杆柔性(双柔性)问题的研究也主要针对地面的机械臂系统[8-9]，或使用奇异摄动法[10]来处理，这与大尺寸柔性空间机械臂产生高幅低频振动的实际情况不符。

在针对机器人的动力学控制中，许多学者提出了如自适应[11]、鲁棒[12]、神经网络[6]等控制方法来解决参数不确定系统的轨迹跟踪问题，但所构建的控制器往往存在计算量偏大的缺点，实际应用非常困难。滑模变结构控制也可以解决参数不确定和外部干扰的系统轨迹追踪控制问题，具有很好的鲁棒性且计算量小，但是滑模变结构控制的最大缺点是系统控制输出在切换时有抖动。一般都认为，将神经网络或模糊控制与滑模变结构控制相结合可有效解决滑模控制中的抖振问题，基于此思路，很多研究人员也提出了多种控制方法，如文献[13-14]分别利用模糊理论和自适应神经网络较好地消除了滑模变结构控制中力矩的抖振。但是模糊理论中合适的模糊规则设计非常困难，而神经网络的自适应学习计算量也非常大，均在实际应用中存在种种限制。

为了解决以上问题，本文利用拉格朗日第二类方程建立了柔性臂杆、柔性关节空间机械臂系统的动力学模型；对柔性关节刚度进行补偿以提高系统的等效刚度；利用反馈线性化技术导出空间机械臂系统追踪期望运动的误差动力学方程，并基于Lyapunov稳定性证明来选择滑模控制参数；建立T-S模糊逻辑模型，简化模糊推理规则，设计系统追踪期望轨迹的改进型T-S模糊滑模鲁棒控制方案；对柔性杆的柔性振动模态设计了直接反馈控制方案；最后，针对系统存在建模误差和外界干扰的情况，对平面二杆空间机械臂系统进行数值仿真分析。

1　双柔性空间机械臂系统动力学分析

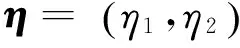
图1　 双柔性空间机械臂系统

由于该柔性臂杆、柔性关节空间机械臂处于太空，无外力作用，系统对惯性坐标系满足动量守恒关系。利用该动量守恒关系，并结合系统柔性臂的弹性应变能、柔性关节的弹性势能，由拉格朗日第二类方程可得到系统动力学方程：

(1)

(2)

2　关节柔性刚度补偿控制输入设计

分析式(1)、式(2)的系统动力学方程发现，系统的机械臂关节存在柔性问题，这将对机械臂跟踪期望运动产生影响。本节针对系统的关节柔性补偿问题进行处理，设计关节柔性补偿器以提高柔性关节的等效刚度，最终提高基体及机械臂跟踪期望轨迹的精度。

对系统动力学方程式(2)进行改写，可得关节驱动电机的力矩动态方程：

(3)

针对该动态方程，设计总的电机控制输入为

τm=Knτn-Kθτθ

(4)

其中，τn为后文待设计的系统轨迹跟踪、柔性模态控制方案，Kθ为对角正定系数矩阵，若Kn选择为

Kn=I+Kθ

(5)

将式(4)代入式(3)，系统关节驱动电机的力矩动态方程则变为

(6)

对比式(3)和式(6)可知，系统关节驱动电机的刚度得到了提升，且Kθ选择得越大，Kn随之增大，系统的等效刚度也随之增大。所以，合适地选择Kθ可对系统关节的柔性进行补偿。

3　系统动力学反馈线性化

上文解决了系统机械臂关节驱动电机的柔性补偿问题后，为了设计系统基体、关节追踪期望运动的控制方案，系统动力学方程改写为

(7)

(8)

(9)

进一步整理有

(10)

利用此误差动力学方程，可进行经典的滑模控制设计。

4　滑模控制器设计

利用双柔性空间机械臂的误差动力学方程(10)，设计滑模控制面为

式中，λ为正定常值系数。

针对以上选定的滑模控制面，本节对控制向量u进行设计来保证系统追踪期望轨迹。在经典的滑模控制当中，可设计u为

u=ure+uS

(11)

所以，当控制系统处于滑模面上，有

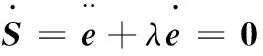
此时uS=0，将系统误差动力学方程式(10)代入上式，ure则可直接设计为

(12)

为了进一步对切换控制向量uS进行设计，选择以下Lyapunov函数：

将V对时间求一阶导数并利用式(10)～式(12)，可得

(13)

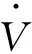
(14)

5　T-S模糊滑模鲁棒控制方案改进设计

利用T-S模糊逻辑来对上节所设计的滑模控制方案进行改进，解决滑模控制抖振的问题，并减小控制系统的计算量。一般地，典型多输入-多输出T-S系统的模糊逻辑规则如下[15]：

Rj：IF x1(t) is Mj1and…and xn(t) is Mjn

THEN yj(t)=zj(X(t),t)，j=1,2,…,r

其中，Rj代表第j个模糊规则，xk和Mjk(j=1,2,…,r；k=1,2,…,n)分别为系统的前件变量和模糊集，r为系统的模糊规则数量。

对于系统的各个独立输入X(t)，利用中心加权解模糊化推理，可获得整个T-S系统的输出向量Y(t)：

其中，Y(t)∈Rr，X(t)∈Rn，而利用直积法，适用度函数wj(X(t))可以定义为

(15)

基于以上T-S模糊模型，针对双柔性空间机械臂系统，对系统基体姿态和关节角的三个控制器设计进行离散化处理。为了使模糊推理尽可能简单，设计单个滑模反馈控制的模糊推理规则库为

其中，i=1,2,3。同样为了使控制系统更加简单，模糊输入变量Si的三角形隶属度函数选择如图2所示。

图2　 三角形隶属度函数

利用中心加权解模糊可得到最终的系统控制输入：

(16)

由此，可分别得到系统载体姿态、两个关节铰的控制输入ui(t)(i=1,2,3)，则系统的整体控制输入为这三个离散控制ui(t)的合成向量。由于所设计的滑模反馈控制的模糊推理规则仅有两条，同自适应控制、神经网络控制等智能控制方法相比，该系统控制输入将具有模糊规则简单、计算量小的显著优点。

6　柔性臂振动模态反馈控制

解决了关节柔性的补偿和基体姿态、机械臂关节的轨迹跟踪问题后，本节仅考虑柔性臂振动模态对系统控制的影响。于是，从系统动力学方程式(7)中可解出

若不考虑系统参数不确定的影响，仅考虑系统的可精确建模模型，则有

(17)

更进一步地，有

(19)

选择以下Lyapunov函数：

将上式对时间求导并利用式(18)，同时忽略系统的参数变动，则有

(20)

τ=τr+τf

(21)

至此，该合成控制器(式(21))加上系统柔性关节刚度补偿控制可完成系统轨迹跟踪控制及柔性关节刚度补偿、柔性模态主动抑制的并行综合控制任务。

7　系统仿真分析

为了检验本文设计的综合控制器的性能，将所设计控制方案应用于图1所示的双柔性空间机械臂系统上。该机械臂系统的参数见表1。

表1　系统惯性参数表

基体姿态及关节角的期望运动轨迹分别设置为

(1)为了说明T-S模糊逻辑控制器的优势，不考虑柔性杆和柔性关节对控制系统的影响，先利用传统的滑模控制器(式(14))来对空间机械臂追踪期望运动进行控制，仿真结果如图3所示。图3显示了在式(14)控制方案控制时，系统控制输入力矩变化情况；若使用本文设计的T-S模糊滑模鲁棒控制方案，即利用式(16)对系统进行控制，系统的控制输入力矩如图4所示。通过对比控制输入力矩(图3、图4)，发现应用T-S模糊滑模控制后，系统控制输入力矩的抖振情况有所缓解；更为重要的是控制输入力矩大幅减小，仅为原来的1/10左右，说明该控制方案还可有效解决控制器饱和的问题。因此，从实用的角度出发，本文所设计的控制方案更接近于工程实际应用。

图3　 采用滑模控制时的控制输入

图4　 采用T-S模糊滑模控制时的控制输入

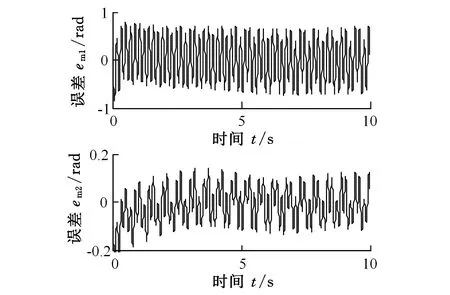
图5　 无柔性关节刚度补偿时的转角误差

(2)为了说明柔性关节刚度补偿的重要性，关闭了系统的柔性关节补偿控制，图5所示为两个驱动电机转角与机械臂杆实际转角的误差；当打开柔性关节刚度补偿时，图6所示为电机转角与臂杆转角的误差。从图6可以明显看出，本文所设计的关节刚度补偿可以很好地解决柔性关节存在时驱动电机与机械臂杆转角误差的问题，达到很好的控制精度。

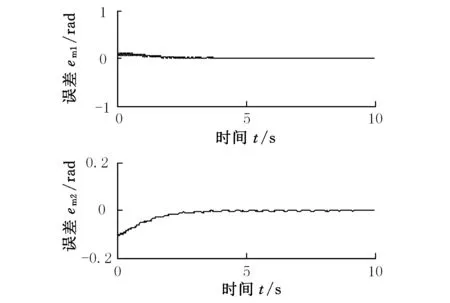
图6　 有柔性关节刚度补偿时的转角误差

(3)在对系统柔性关节刚度进行补偿后，通过切换柔性杆振动模态控制的输入，得到图7～图10的仿真结果。图7所示为未对柔性杆振动进行控制时的柔性模态，图8所示为对柔性杆振动进行主动控制时的柔性模态，图9、图10所示为系统追踪期望轨迹的最终跟踪情况。对图7、图8进行对比，发现本文所设计的振动控制方案可有效地抑制柔性杆的振动模态，2s后柔性模态基本收敛于0，避免了柔性杆振动对系统控制精度的影响。而图9、图10则说明了所设计的综合控制方案可保证系统稳定、高精度地追踪其期望运动。

图7　 无柔性杆振动控制时的柔性模态

图8　 有柔性杆振动控制时的柔性模态

图9　 基体姿态追踪情况

图10　 机械臂关节角追踪情况

8　结论

(1)针对柔性臂杆、柔性关节空间机械臂系统存在外界干扰及系统参数不确定而导致的建模误差情况，本文结合反馈线性化和T-S模糊逻辑推理系统，设计了空间机械臂追踪期望运动的改进型T-S模糊滑模控制方案，大幅缓解了控制器饱和的问题，同时由于所设计的T-S模糊推理规则仅有两条，该控制方案不仅能解决参数不确定的问题，而且具有计算量小、便于实际应用的优点。

(2)针对系统柔性关节问题，设计了柔性关节刚度补偿控制方案，有效解决驱动电机实际转角与关节转角之间存在误差的问题；针对柔性臂杆的振动，设计了柔性模态直接反馈控制方案，对柔性振动模态进行主动控制，实现了双柔性并行控制。

(3)为了验证所设计综合控制方案的有效性，逐步对不同工况下的空间机械臂进行仿真分析，仿真结果表明，该T-S模糊滑模鲁棒控制方案可保证系统在同时存在参数变动及外界干扰的情况下仍能准确、稳定地追踪期望运动，解决了柔性关节和柔性臂杆的振动问题。

[1]ReviewofUnitedStatesHumanSpaceflightPlansCommittee.SeekingaHumanSpaceflightProgramWorthyofaGreatNation[R].WashingtonD.C.:NASA,2009.

[2]XuWenfu,LiangBin,XuYangsheng.SurveyofModeling,Planning,andGroundVerificationofSpaceRoboticSystems[J].ActaAstronautica, 2011,68(68):1629-1649.

[3]ColeshillE,OshinowoL,RembalaR,etal.Dextre:ImprovingMaintenanceOperationsontheInternationalSpaceStation[J].ActaAstronautica,2009,64 (9/10): 869-874.

[4]苏文敬,吴立成,孙富春,等.空间柔性双臂机器人系统建模、控制与仿真研究[J].系统仿真学报,2003,15(8): 1098-1100.

SuWenjing,WuLicheng,SunFuchun,etal.DynamicsModeling,ControlandSimulationforFlexibleDual-armSpaceRobot[J].JournalofSystemSimulation,2003,15(8):1098-1100.

[5]王从庆,张承龙.自由浮动柔性双臂空间机器人系统的动力学控制[J].机械工程学报,2007, 43(10): 196-200.

WangCongqing,ZhangChenglong.DynamicControlofaFree-floatingFlexibleDual-armSpaceRoboticSystem[J].ChineseJournalofMechanicalEngineering,2007,43(10):196-200.

[6]ZhangWenhui,HuXiaoping,FengYamin.AdaptiveControlforFree-floatingSpaceFlexibleRobotBasedonFuzzyCMAC[J].JournalofInformationandComputationalScience,2014,11(1): 141-149.

[7]UlrichS,SasiadekJZ.ExtendedKalmanFilteringforFlexibleJointSpaceRobotControl[C]//Proceedingsofthe2011AmericanControlConference.Piscataway:IEEE,2011: 1021-2016.

[8]ShihabudheenKV,JacobJ.CompositeControlofFlexibleLinkFlexibleJointManipulator[C]//2012AnnualIEEEIndiaConference.WashingtonD.C.:IEEE,2012:827-831.

[9]VakilM,FotouhiR,NikiforukPN.ANewMethodforDynamicModelingofFlexible-linkFlexible-jointManipulators[J].JournalofVibrationandAcous-tics,2012,134(1): 14503-14513.

[10]梁捷,陈力.柔性关节-柔性臂空间机器人的神经网络自适应反演控制及双重柔性振动抑制[J].计算力学学报, 2014,31(4): 459-466.

LiangJie,ChenLi.NeuralNetworkAdaptiveBacksteppingControlandDoubleFlexibleVibrationActiveHierarchicalSuppressionofSpaceRobotwithFlexible-jointandFlexible-link[J].ChineseJournalofComputationalMechanics,2014,31(4): 459-466.

[11]张福海,付宜利,王树国.惯性参数不确定的自由漂浮空间机器人自适应控制研究[J].航空学报,2012, 33(12): 2347-2354.

ZhangFuhai,FuYili,WangShuguo.AdaptiveControlofFree-floatingSpaceRobotwithInertiaParameterUncertainties[J].ActaAeronauticaetAstronauticaSinica,2012, 33(12): 2347-2354.

[12]GuoShengpeng,LiDongxu,MengYunhe,etal.ReactionlessRobustFinite-timeControlforManipulationofPassiveObjectsbyFree-floatingSpaceRobots[J].Chin.Phys.B, 2014, 23(5): 347-354.

[13]刘希, 孙秀霞, 刘树光，等.非脆弱递归滑模动态面自适应神经网络控制[J].控制理论与应用, 2013, 30(10): 1323-1328.

LiuXi,SunXiuxia,LiuShuguang,etal.Non-fragileRecursiveSlidingModeDynamicSurfaceControlwithAdaptiveNeuralNetwork[J].ControlTheory&Applications, 2013,30(10): 1323-1328.

[14]洪昭斌,陈力.漂浮基双臂空间机器人系统的模糊神经网络自学习控制[J].机器人,2008, 30(5): 435-439.

HongZhaobin,ChenLi.FuzzyNeuralNetworkSelf-learningControlofFree-floatingDual-armSpaceRobotSystem[J].Robot,2008, 30(5):435-439.

[15]HyunCH,ParkCW,KimS.TSFuzzyModelBasedIndirectAdaptiveFuzzyObserverandControllerDesign[J].Inf.Sci.,2010,180(11): 2314-2327.

(编辑陈勇)

T-S Fuzzy Trajectory Tracking and Double-flexible Parallel Control of Flexible-link Flexible-joint Space Manipulator

Hong Zhaobin1Chen Li2Li Wenwang1

1.Xiamen University of Technology, Xiamen,Fujian,361024 2.Fuzhou University, Fuzhou, 350108

Aimed at the problems of flexible-link flexible-joint space manipulator with parameter uncertainties and external disturbances to track the desired motion, the T-S fuzzy control and double-flexible vibration parallel control were proposed. Firstly, a joint flexibility compensation controller was introduced to improve the equivalent stiffness of each joint. Secondly, the error dynamic equations were obtained based on feedback linearization in the trajectory tracking procedure, and control parameters of fuzzy control was selected by Lyapunov stability theory.Subsequently, the fuzzy sliding mode control was improved with simple T-S fuzzy rules. The great advantage of proposed control is free of undesirable chattering phenomenon in sliding mode control and light burden of computations. Then, the double-flexible parallel control was presented to suppress the vibration of flexible links. Finally, the simulation results on a space manipulator demonstrate the validity of the proposed control scheme.

space manipulator;flexible-link flexible-joint;parameter uncertainty;T-S fuzzy sliding mode control;double-flexible parallel control

2015-10-10

福建省自然科学基金项目(2013J05021)；福建省科技计划重大重点项目(2012H0041)；福建省教育厅A类项目(JA15382)

TP241

10.3969/j.issn.1004-132X.2016.15.006

洪昭斌，男， 1982年生。厦门理工学院机械与汽车工程学院讲师、博士。主要研究方向为空间机器人动力学及控制。陈力，男， 1961年生。福州大学机械工程及自动化学院教授、博士研究生导师。李文望，男， 1966年生。厦门理工学院机械与汽车工程学院教授。