支持向量机与K-均值聚类融合算法的研究

田飞，于威威（上海海事大学，上海　201306）

支持向量机与K-均值聚类融合算法的研究

田飞，于威威
（上海海事大学，上海201306）

传统的支持向量机分类算法随着样本规模增大、支持向量数量增多时，其分类过程所消耗的时间也会随之增加。为此，提出一种改进算法，将K-均值聚类算法与支持向量机融合。将标准支持向量机训练后得到的支持向量集进行特定比例的K均值聚类操作，把聚类的中心作为新的支持向量，再用二次规划方法求解得到新的分类决策函数。实验结果表明，该分类算法有效地减少计算时间，提高分类速度，尤其在训练集规模庞大、支持向量数量较多的情况下，效果会更加明显。

支持向量机；支持向量；K均值聚类；二次规划

0　引言

支持向量机（Support Vector Machine，SVM）算法是在统计学习理论［1］的基础上提出的，在处理小样本分类问题是具有其他分类算法不具备的优势。它最初于20世纪90年代由Vapnik提出，是近几年来机器学习的一项重大研究成果，SVM在很大程度上解决了过学习、高维数和局部极小点等传统困难。此外，由于其优秀的性能以及其优良的范化能力，使其在很多领域中得到长足的发展，并被广泛应用于网络入侵检测、文本识别、人脸表情图像识别等领域。人们对于支持向量机算法的研究已经相当成熟，在加速训练过程方面近年来已经取得了一定的研究成果：如Platt提出的 SMO （Sequential Minimal Optimization）方法［2］、以及Suykens等人提出的最小二乘支持向量机［3］（Least Squares Support Vector Machines，LS-SVM）和Osuna等的Chunking方法［4］以及文献［5］使用KNN预选取样本的方法等，这些方法对分类速度的提高没有任何影响。文献［6］提出的RSVM（Reduced Support Vector Machines）算法是基于随机地选取样本集中的一个子集进行训练，该方法在一定程度上减少SVM训练时间、加快训练速度。但是由于样本规模减小而损失了部分支持向量，导致其分类精度有所下降。所以，研究如何在尽量减小分类精度损失的前提下，将原始支持向量的数量尽量减少是本文需要解决的一个问题。

在提高SVM分类速度这个方向，许多研究人员也提出了相应的减少支持向量算法：如Burges等人提出的一种提高分类速度方法［7］，该方法中的向量集既不是训练样本也不是支持向量，而是经过变换得到的特殊向量。文献［8］提出了ν-SVM，并指出参数ν是支持向量的个数和训练样本个数的比率（支持向量率）的下界。刘向东、陈兆乾等人提出的快速的支持向量机分类算法 FCSVM［9］（Fast Classification for Support Vector Machines）是通过变换矩阵的方式来减少分类函数中的支持向量，但是该变换方式需要通过不断的迭代来找出合适的支持向量划分集。本文提出了一种减小支持向量，提高分类速度的算法：即将K均值聚类算法引入SVM中，将标准的SVM训练得到的支持向量集通过聚类算法按照特定的比例压缩，再根据求解二次规划问题来求解出新的稀疏后的支持向量对应的权重系数，最终得到精简后的新的SVM快速决策函数。

1　原理概述

1.1支持向量机算法

设样本及其值表示为 （xi，yi），其中 i=1，2，…，l，xi∈Rn，yi∈｛-1，1｝，在线性不可分的情况下，SVM将数据映射到一个特征高维空间Ø（x）=（φ1（x），φ2（x），…，φN（x））中，并且构造出最优超平面y（x）=sgn［w·（x）+b］。以此来实现非线性分类到高维特征空间中的线性分类的一个转化，即在约束条件为yi［Ø（xi）·w+b］≥1-ξ的情况下，使‖w‖最小化的问题。也就是：

其中ξi≥0，i=1，2，…，l，c为给定常量

为了解决约束最优化问题并转化为其对偶问题，引入式（2）所示的拉格朗日函数：

其中ai，γi是拉格朗日乘子ai≥0，γi≥0，i=1，2，…，l。由于该优化问题存在不等式约束，因此，对w，b，ξ求偏导并令其等于零，得：

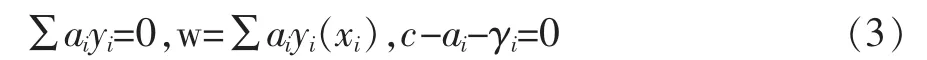
将公式（3）代入公式（2），那么该问题就转化为求最大化下面函数（寻优函数）：

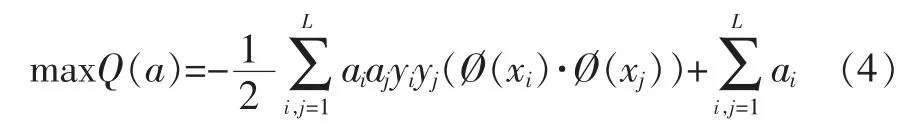
选取核函数K（xi，xj）求解最优化问题：

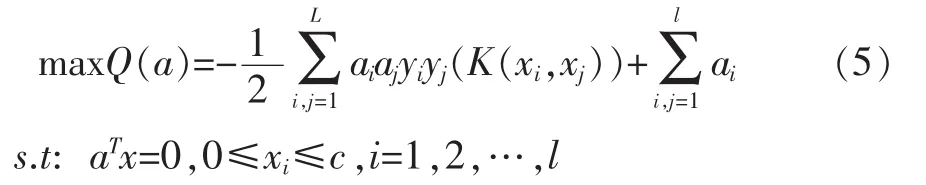
这是一个标准的二次规划问题 （Quadratic Programming，QP），再根据KKT条件，最优解满足，

其中SV表示支持向量。

最后的决策函数为：

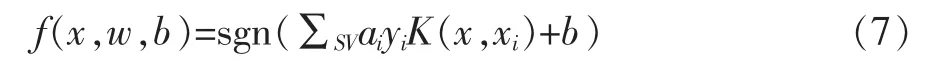
1.2K-均值聚类算法

K-均值聚类算法属于聚类方法中一种应用最广泛的划分算法，它以K为聚类类别数，把n个对象划分为k个簇，从而使类内间高内聚，类间低耦合。其主要过程如下：

（1）给定点集X=｛x1，x2，…，xl｝，X∈Rn，并给定簇数K，选取精度ε＞0，置m=0。假设选取前K个初始聚类中心为：。

2　算法设计

从上述公式（7）可以直观地看出，支持向量的多少将决定SVM分类过程的计算量的大小。传统的SVM分类函数中包含了全部的支持向量，以致于其分类速度必然较慢，所以提高分类速度的关键就在于减少SV的数量。那么该如何减少SV的数量？因此，本文提出将K-均值聚类算法引入支持向量机算法中，其基本思想如下：

3　实验结果及分析

为了验证本文算法的分类性能，选取UCI标准数据集［10］上的The Insurance Company Benchmark（COIL 2000）作为实验所用的数据。该数据集包含了7822个保险公司客户的记录，每个记录由86个属性组成，包含社会人口数据（属性1-43）和产品的所有关系（属性44-86）。社会人口数据是由派生邮政编码派生而来的，生活在具有相同邮政编码地区的所有客户都具有相同的社会人口属性。其中5822个客户的记录作为训练样本集，2000个客户的记录作为测试样本集，将本文算法与标准SVM算法进行了对比。实验中选择了径向基函数（RBF）作为分类器的核函数，支持向量机的惩罚因子C=500，训练后得到的支持向量个数为1333。并且重复10折交叉验证法［11］对比实验：在标准SVM训练得到支持向量的基础上，调节本文算法中的压缩比l2/l1及相关系数，使得该算法在保持分类精度差异较原始SVM不明显的前提下，尽量减少支持向量，加快分类速度。对比实验结果参见表1。

从表1的实验结果可以看出，相对于传统SVM算法，在保持分类精度无显著差异的前提下，本文改进的算法通过调节部分参数使分类函数中的支持向量数尽可能达到最少，从而在分类时间上明显比标准SVM快；从改进前后速度比较来看，本文提出的方法分类速度最高提高了47.03%。

4　结语

本文从对标准SVM训练后得到的支持向量集，并按照特定比例压缩的方法来减小分类的时间，提高支持向量机的分类速度这一思路出发。提出了一种新的改进的支持向量机算法，该算法使用K-均值聚类算法通过特定比例对原始支持向量集进行压缩，以此来得到新的稀疏化后的支持向量集，然后按照误差最小原则重新构造了一个新的分类决策函数，从而使计算量减少到最小，使分类速度提高。通过实验对比，本文算法比传统支持向量机算法具有更好的实用性，尤其是在数据规模较大或者是支持向量数量较多的情况下，其分类效果会更加明显。

表1　实验对比结果

［1］Vapnik V.The Nature of Statistical Learning Theory［M］.New York：Springer-Verlag，1995.

［2］Platt J C.Fast training of Support Vector Machines Using Sequential Minimal Optimization.Advances in Kernel Methods Support Vector Learning，California，USA，1999∶185-208.

［3］Suykens J A K，Vandewalle J.Least Squares Support Vector Machine Classifiers.Neural Processing Letters，1999，9（3）∶293-300.

［4］KEERT HIS，GILBERTE.Convergence of a Generalized SMO Algorithm for SVM Classifier Design［J］.Machine Learning，2002，46（1 /3）∶3 51-36 0

［5］韩德强，韩崇昭，杨艺.基于K-最近邻的支持向量预选取方法.控制与决策，2009，24（4）∶494-498

［6］LEE Y J，MANGASARIAN O L.RSVM∶Reduced Support Vector Machines［R］.Wisconsin∶Data Mining Institute，Computer Sciences Department，University of Wisconsin，2000.

［7］Burges C J C and Sch？lkopf B.Simplified Support Vector Decision Rules.In 13th International Conference on Machine Learning，Bari，Italy 1996∶71-77.

［8］Schölkopf B，Smola A J，Williamson R C，et al.New Support Vector Algorithms.Neural Computation，2000，12（5）∶1207-1245.

［9］刘向东，陈兆乾.一种快速支持向量机分类算法的研究.计算机研究与发展，2004，41（8）∶1327-1332.

［10］Frank A，Asuncion A.UCI Machine Learning Repository.Http∶//www.ics.uci.edu.html，2007.

［11］Kohavi R.A study of Cross-Validation and Bootstrap Foraccuracy Estimation and Model Selection［C］.Proc 14th Joint Int.Conf.Artificial Intelligence.San Mateo，CA：Morgan Kaufmann，1995：1137-1145.

Support Vector Machine；Support Vectors；K-Means Clustering；Quadratic Programming（QP）

Research on Support Vector Machine and K-means Clustering Fusion Algorithm

TIAN Fei，YU Wei-wei
（Shanghai Maritime University，Shanghai 201306）

The traditional classification algorithm of support vector machine（SVM）as the sample size increases，the increase in the number of support vectors（SVs），the classification process consumes time will also increase.Therefore，proposes an improved algorithm K-mean clustering algorithm and SVM fusion.The standard SVM training support vector specific proportion of the K-means clustering and the cluster center as a new support vector，uses quadratic programming method to solve the obtained new support vector coefficients.Experimental results show that the classification algorithm can effectively reduce the computing time and improve the classification speed，especially in the case of large training set size and the number of support vectors，the effect is more obvious.

1007-1423（2016）20-0035-04

10.3969/j.issn.1007-1423.2016.20.007

田飞（1990-），男，安徽六安人，硕士研究生，研究方向为数字图像处理，模式识别

于威威（1978-），女，山东淄博人，博士研究生，副教授，研究方向为模式识别、计算机图像处理、数据挖掘等

2016-04-12

2016-07-10