等效源法声全息中求解正则化参数的一种新方法

蔡鹏飞，陈德兵，姚　波，朱永洪（重庆车辆检测研究院 国家客车质量监督检验中心，重庆　401122）

等效源法声全息中求解正则化参数的一种新方法

蔡鹏飞，陈德兵，姚波，朱永洪
（重庆车辆检测研究院 国家客车质量监督检验中心，重庆401122）

针对等效源法近场声全息声场重建中Tikhonov最优正则化参数选取问题，本文引入Bayesian正则化准则法进行求解，并与GCV法和L-curve法进行仿真对比分析。结果显示，Bayesian正则化准则法在宽频带内有优异的重建性能。进一步的计算及试验表明，该方法能够稳定准确地实现声场重建。

等效源；近场声全息；Bayesian；正则化

基于声阵列的噪声源识别技术能够快速高效地实现声场重建［1-4］。目前，等效源法声全息［5］在声场重建中得到广泛应用。其通过均匀密度分布的单极子等效实际声源，将自由场格林函数作为声源表面声学量与测量声压的传递函数来构建求解方程，对于不同拓扑结构的声源表面及阵列形式均有很好的适应性［5］。

然而对于声场重建问题，常需采用正则化方法来获得最优解。Tikhonov正则化作为一种最常用的正则化方法在近场声全息（NAH）中已得到广泛应用［6］。最优正则化参数的选取是该方法的重要步骤，通常采用L-curve法［7］，广义交叉验证（GCV）法等［8］。但不同的正则化参数选取方法没有绝对的优劣之分，往往需视不同的研究内容而选择最优的正则化参数选取方法。虽然各种方法已得到成功运用，但同种方法的重建效果大多因研究问题背景而异，目前还没有一种适应性最好的正则化参数选取方法［9-10］。

近年来出现了一种新的正则化参数选取方法——Bayesian正则化准则［11］。文献［12］将ESM法和Bayesian法作了理论对比，而在正则化参数确定方面，ESM采用GCV和L-curve法，Bayesian法采用Bayesian正则化准则。本文受上述文献启发，基于等效源法近场声全息，在声场逆向求解过程中提出采用Bayesian正则化准则来选择最优的正则化参数，并与采用L-curve、GCV两种正则化参数选取方法的声场重建结果进行对比，最后通过仿真分析及试验，验证了Bayesian正则化准则在等效源法声全息中应用的正确性与有效性。该方法为汽车工程中噪声源识别领域诸如进气噪声、排气噪声、发动机噪声、室内噪声等提供了一种便捷高效的识别方法。

1　基本理论

1.1等效源法近场声全息

等效源法近场声全息的基本思想是用一系列分布在振动体内部或表面的等效源如单极子产生的声场替代振动体实际辐射声场。通过全息面所测声压数据反向求解各等效源源强，利用声学传递函数即可求得声场中各声学量。假设全息面分布M个麦克风，声源面布置N个等效源，全息面测点声压可以表示为矩阵形式：

式中：p为麦克风所测声压列向量；q为等效源强度列向量；G是等效源强到测点声压的传递矩阵，其中G（m，n）=jρckg（rm，r）n，ρ为空气密度，c为声速，k是波数，rm为第m个测点位置矢量，rn为第n个等效源位置矢量，g（rm，r）n为自由场格林函数：

事实上，为获得声源的局部信息或细节信息，需按声源形状布置多个等效源。本文旨在研究等效源数多于测量点数的情形，此时式（1）为欠定方程，没有特解，通过Tikhonov正则化技术寻求式（1）的最优解［12］：

式中：H表示转置共轭，η为正则化参数，I为单位矩阵。对传递矩阵进行奇异值分解：

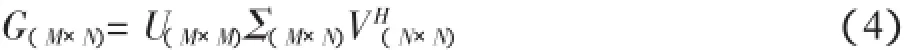
其中，U为左奇异向量酉矩阵；Σ=［S 0］为奇异值矩阵，且S=diag（σ1，…σM）为对角矩阵，σ为奇异值，且σ1≥…≥σM≥0；V为右奇异向量酉矩阵。将式（4）带入式（3），化简得式（1）的最优解：

由式（5）可知，求得等效源强度后，便可确定声场空间任一点的声压等声学量。

1.2Bayesian正则化准则

求解式（5）中声源强度，正则化参数η的选取尤为重要，若记式（5）为q=VΣRUHp，则：

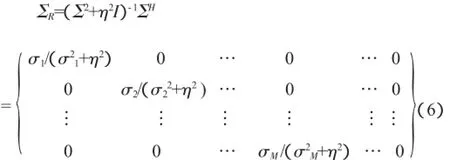
从式（6）可以看出：η选择过大，造成小奇异值项对实测声压过滤波，导致解失真；η选择过小，对于受噪声污染的声压数据，小奇异值项对噪声干扰敏感，引起重建误差。正则解的精度对正则化参数有直接的依赖性，因此选择最优的正则化参数才能保证最优解。Bayesian正则化准则［11-12］是一种新的高效稳健的正则化参数选取方法，通过最小化如下函数获得最优正则化参数：

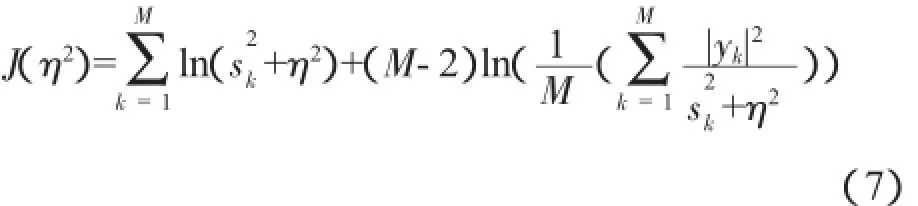
式中：sk为矩阵S的第k个奇异值，yk为向量y的第k个元素，且：

2　正则化参数选取方法比较及试验验证

为探究本文引入的Bayesian正则化准则在等效源法声全息中的声场重建性能，将其与L-curve法，GCV法进行数值仿真对比研究，比较三种方法在不同全息测量距离、声场信噪比、重建频率方面对声场重建结果的影响，采用相对误差衡量各自的重建性能：

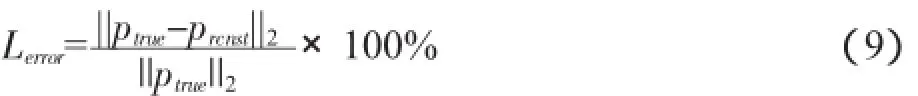
式中：Lerror为相对误差；ptrue，prcnst分别为真实声压和重建声压，单位为Pa；||||2表示矩阵的2范数。

仿真试验中，测量面为36通道的Brüel&Kj∂er公司、直径0.65 m的平面传声器阵列，声源等效为21×21个不同强度的单极子点声源，单位强度点声源位于声源面几何中心，全息距离用Zh表示，传声器阵列及等效源布置物理模型如图1所示。

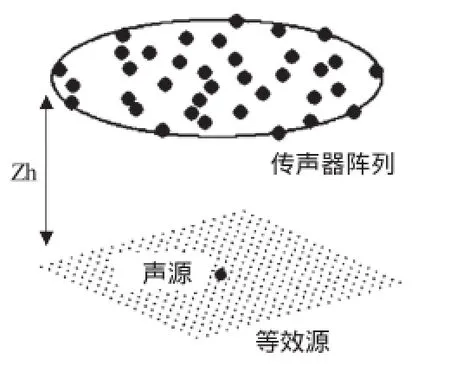
图1　仿真试验模型

2.1不同测量距离时的对比分析

对于图1所反映的声场求逆过程是欠定问题的求解，利用式（5）在200 Hz～3 000 Hz频带范围内进行计算，并加入60 dB的高斯白噪声以模拟测量噪声。图2给出了测量距离分别为0.1～0.3 m（间隔0.05 m）时，三种参数选取方法的重建声压相对误差结果。可以看出：

1）三种方法的重建结果表现出一致性，即均呈现低频误差小，高频误差大，且随测量距离增大相对误差增大的趋势，这与近场声全息适用于中低频声源识别的结论相吻合。

2）Bayesian正则化准则法在低频近距离测量时有优异的重建性能，而高频远距离测量时重建误差在10%以内，整个频段内都有较好的重建结果。

3）GCV法与Bayesian法有相似的重建性能，但在测量距离较远时高频识别结果出现波动幅度较大的震荡。究其原因，主要是某些频率点处，如2 700 Hz时，GCV函数没有出现明显的最小值拐点，而在拐点出现前，其函数值如图3（a）虚线椭圆标注的部分，曲线基本没有变化，导致最小的GCV函数值对应多个变量，从而使正则化参数的选取出现不稳定性。

4）L-curve法在低频靠近声源测量时也有较好的重建性能，但在高频段重建结果较差，且中低频有突变。进一步的分析表明，以全息距离0.2 m，频率2 800 Hz为例，此时L曲线及其曲率分别如图3（b）中的上、下图所示，残留范数lg（||Gq-p||）与解范数lg（||q||）的平衡点出现在曲线最大曲率处，如图3（b）上图箭头所示处，此时出现过正则化，导致正则化解失去了大量高频空间频率信息，仅剩下奇异值很大的几项，导致重建结果不准确。而当全息距离为0.15 m时，亦由于过正则化，致使重建结果不稳定。

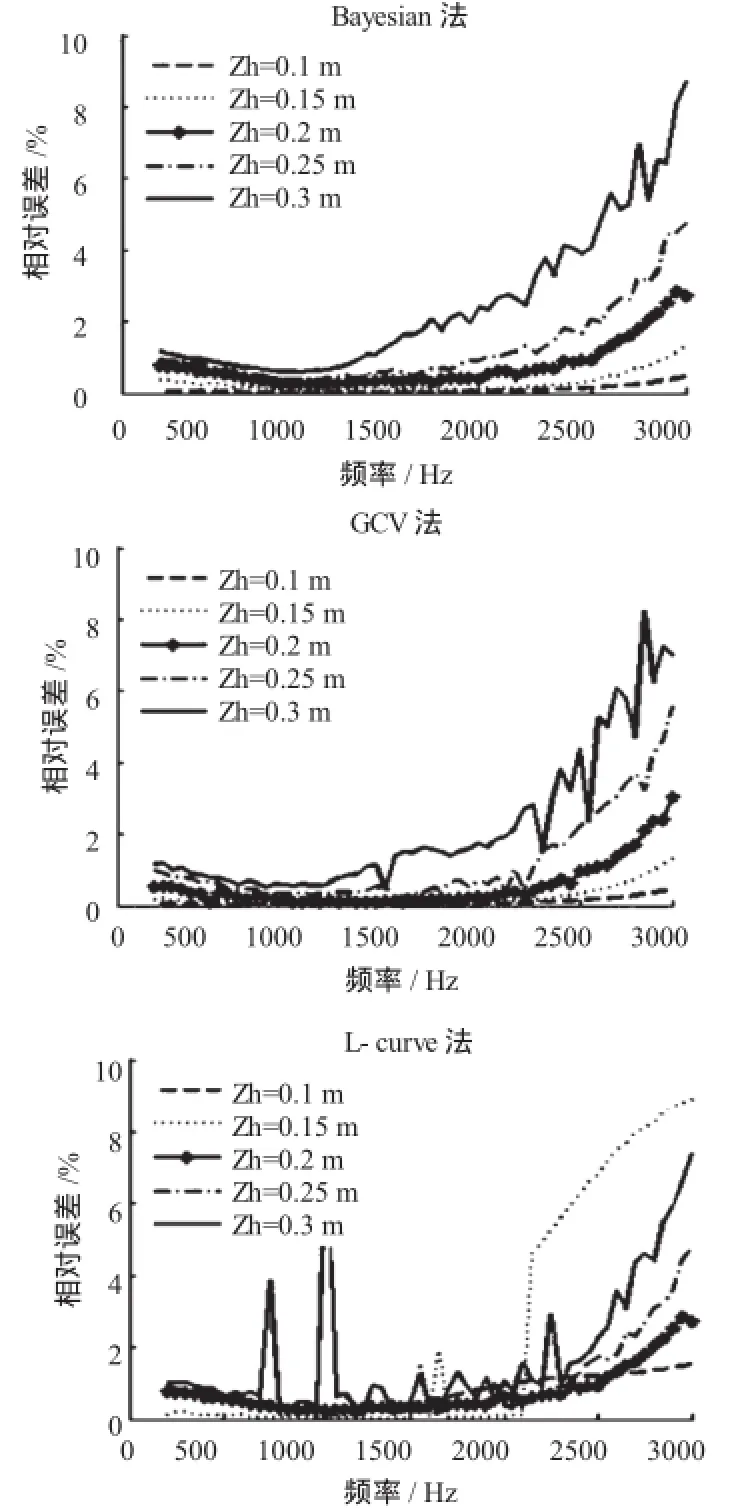
图2　不同全息距离时的相对误差曲线

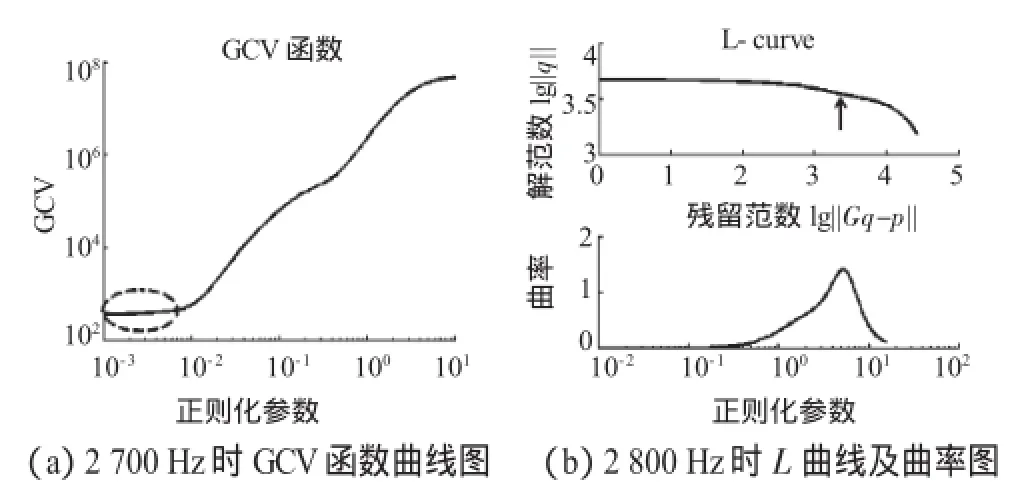
图3　GCV函数及L曲线

2.2不同噪声水平时的对比分析

为进一步探究不同噪声环境下三种方法的重建性能，模拟信噪比SNR为30 dB、40 dB、50 dB、60 dB、70 dB的声场噪声环境，进行多次仿真试验，其中全息测量距离为0.2 m，0.05 m处的声压相对误差计算结果如图4所示。对比可知：Bayesian正则化准则法在全频段不同信噪比配置下都有很好的重建性能；GCV法在信噪比较低时重建结果出现震荡，重建性能不稳定；L-curve法在高频且信噪比过大时重建结果出现较大偏差，这是由于欠正则化致使测量数据对微小的噪声干扰产生较大的扰动。

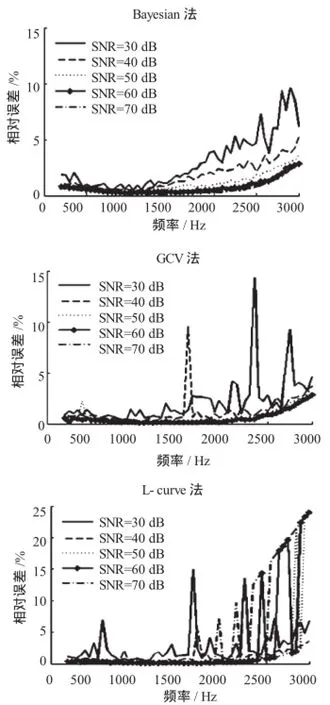
图4　不同信噪比时的相对误差

以上仿真结果表明，Bayesian正则化准则法对全息距离、声源频率以及声场信噪比都有很好的适应性，能够选择最优的正则化参数，从而避免正则解因过正则化和欠正则化带来的误差；GCV法虽有较好的重建性能，但在高频段以及不理想的噪声环境下由于GCV函数最小值的不确定性致使重建结果容易出现震荡；L-curve法在低频且靠近声源面测量时，通过L曲线最大曲率选取的正则化参数能稳定正则解，但宽频带内，尤其是高频段，其重建性能较差。

2.3试验验证

为验证Bayesian正则化参数选取方法在等效源法近场声全息中应用的正确性与有效性，进行了仿真分析与对比试验。仿真及试验中，在距离声源平面0.1 m的位置进行测量，在距离声源面0.05 m的重建面上将重建计算结果与实际测量值进行比对。声源为位于支架中心位置的扬声器，其由近似的稳态白噪声激励，设置21×21个等效源，等效源间距为0.03 m×0.03 m。试验采用Brüel&Kj∂er公司、直径0.65 m、集成4958型传声器的36通道COMBO阵列采集声信号，基于等效源法近场声全息原理完成重建计算，并与试验测量值进行对比，结果如图5所示。

图5　试验结果

图5中SPL表示声压级，其中上图为距离声源表面0.05 m处的试验测量值，下图为利用Bayesian正则化准则的重建值。结果显示，声学成像中心都出现在声源中心位置，能够准确定位声源。再次与GCV、L-curve法计算结果相比，如图6所示，在感兴趣的500 Hz～3 000 Hz频率范围内，幅值差异较为明显。图中带“+”的实线表示测得的不同频率的最大声压级，点线、实线、点划线分别表示用Bayesian正则化准则、GCV、L-curve法计算得到的最大声压级。可以看出点线和带“+”的实线吻合较好，而实线和点划线相对带“+”的实线有较大偏差。这表明Bayesian正则化准则法计算结果更能准确反映试验测量值，GCV、L-curve法计算结果相对试验测量值而言较差，尤其在1 500 Hz～2 000 Hz范围内以及3 000 Hz附近，幅值差异达到最大。这进一步验证了Bayesian正则化准则法能准确有效地完成声场重建。

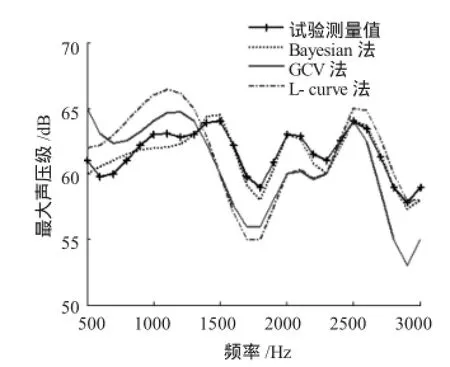
图6　最大幅值

3　结论

综合仿真分析和试验结果表明：总体上Bayesian正则化准则与GCV、L-curve法一样，在低频低噪声水平重建误差小，高频远距离测量时误差较大。但基于Bayesian正则化准则法在全频带内都能选择最优的正则化参数，声场重建结果精度高，且无需先验的信噪比作为输入参数。Bayesian正则化准则法在等效源法近场声全息中能够稳定精确地实现声场重建，为等效源法声全息声场逆问题的求解提供了一种新的指导方法。

［1］Francesco Martellotta.On the use of microphone arrays to visualize spatial sound field information［J］.Applied Acoustics，2013，74（8）:987－1000.

［2］Donavan P R，Rymer B，Blake W.Localization of truck noise sources under passby conditions using acoustic beamforming methods［J］.SAE International Journal of Commercial Vehicles，2009，2（1）:128－139.

［3］褚志刚，杨洋，王卫东，等.基于波束形成方法的货车车外加速噪声声源识别［J］.振动与冲击，2012，31（7）：66－70.

［4］邓江华，顾灿松，刘献栋，等.基于声阵列技术的汽车噪声源识别贡献量分析［J］.振动工程学报，2010，23（6）：630－635.

［5］Pinho M E V，Arruda J R F.On The Use of the Equivalent Source Method for Nearfield Acoustic Holography［J］.ABCMSymposiumSeries in Mechatronics，2004，1：590-599.

［6］Williams E G.Regularization methods for near-field acoustical holography［J］.J.Acoust.Soc.Am，2001，110（4）：1976－1988.

［7］Hansen P C，O'Leary D P.The use of L-curve in the regularization of discrete ill-posed problems［J］.SIAMJournal on Scientific Computing，1993，14（6）:1487-1503.

［8］Golub G H，Heath M，Wahba G.Generalized cross-validation as a method for choosing a good ridge parameter［J］.Technometrics，1979，21（2）:215-223.

［9］Leclere Q.Acoustic imaging using under-determined inverse approaches:Frequency limitations and optimal regularization［J］. Journal ofSound and Vibration，2009，321（3-5）:605-619.

［10］Magalhaes M B S，Tenenbaum R A.Sound Sources Reconstruction Techniques:A Review of Their Evolution and New Trends［J］.Acta Acustica united with Acustica，2004，90（2）:199 -220.

［11］Antoni J.Bayesian focusing：a unified approach to inverse acoustic radiation［C］.Proceedings of ISMA，2010，Leuven，Belgium.2010.

［12］Pereira A，Leclere Q，Antonio J.A theoretical and experimental comparison of the equivalent source method and a Bayesian approach to noise source identification［C］.4th Berlin BeamformingConference，2012.

修改稿日期：2016-04-23

A New Method of Solving Regularization Parameters in Acoustic Holography Based on Equivalent Source Method

Cai Pengfei，Chen Debing，YaoBo，Zhu Yonghong
（ChongqingVehicle Test&Research Institute，National Coach QualitySupervision&TestingCenter，Chongqing401122，China）

Accordingtothe choice ofthe optimal Tikhonov regularization parameters in near field acoustic holography reconstruction based on equivalent source method，the authors introduce the Bayesian regularization criterion method to solve the above problem，and compare it with GCV and L-curve methods by simulation analysis contrast. The results show that Bayesian regularization criterion method has an excellent reconstruction performance in wide frequency band.Further calculation and experiment showthat Bayesian regularization criterion method can achieve stable and accurate sound field reconstruction.

equivalent source；near filed acoustic holography；Bayesian；regularization

U467.4+93；U463.6

A

1006-3331（2016）04-0009-04

蔡鹏飞（1989-），男，硕士；主要从事车辆NVH控制理论及应用研究，汽车整车检测等工作。