一种采用剩余服务时间的异构网络选择算法
杜 白,李红艳
(西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071)
一种采用剩余服务时间的异构网络选择算法
杜 白,李红艳
(西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071)
针对异构网络环境中的网络选择问题,提出了使用剩余服务时间的异构网络选择算法.大部分现有的工作都是在一个时刻点只考虑用户或者网络收益全局的最优化,而没有考虑最优分配结果对后续到达业务影响的问题.剩余服务时间的概念将这个影响引入文中提出的建模中,从而得到一个在长时间尺度上更好的网络选择方案.文中使用非合作博弈对网络进行建模,并证明了文中提出的博弈模型的纳什均衡点同时也是全局的最优解;最后,利用李雅普诺夫理论证明了文中算法的稳定性.仿真结果说明,剩余服务时间的引入能够使网络的性能得到改善,降低了用户的阻塞率,提高了网络总的收益.
异构网络;网络选择;非合作博弈;李雅普诺夫;剩余服务时间
近年来,新式无线网络接入技术快速发展带来了很多新问题,比如异构环境中的网络发现、网络选择和网络切换等[1].网络选择是其中一个关键性问题,直接影响整个网络资源的利用率和用户体验的满意度.网络选择中,为了得到不同参数合理的权重,找到合适的折中点,很多数学方法,比如博弈论、多目标优化、效应函数、层次分析法和模糊逻辑等被广泛使用[2-6].
博弈论专门用于解决博弈参与者的均衡问题,非常适用于网络选择场景[7-8].文中使用非合作博弈研究新用户到达时如何进行博弈,使整个网络的收益达到最大.目前已有的工作大多考虑在用户到达时,如何进行网络选择使全网达到最优,而没有考虑当前的决策对网络后续性能的影响.这种做法会导致网络资源在长时间尺度上的分配达不到最优.笔者使用剩余服务时间的概念,将新用户的网络选择对整个网络长时间的影响引入模型中,使用李雅普诺夫稳定理论和排队论进行建模,并证明在网络的容量域内,文中提出的算法具有稳定性[9-10].仿真的结果证明了文中算法的有效性,降低了用户的拒接概率,减少了网络中数据的队列长度,使业务数据在整个系统中的分布更加均衡,提高了网络业务容量.
1 系统的非合作博弈模型和网络选择算法
如图1所示,异构网络的场景包含1个蜂窝网和两个无线局域网(Wireless Local Area Network,WLAN),3个网络重叠覆盖.用户在不同的区域有不同的可接入网络.用ui表示用户i,Nj表示接入网j,其中,N1表示蜂窝网,N2和N3分别表示两个WLAN网.假设网络分时隙运行,用户以泊松过程随机到达整个网络.每个用户需求的最小带宽用βi表示,如果用户获得的带宽小于βi,则认为ui的满意度为0,也就是支付函数为0,后面会给出支付函数的具体定义.
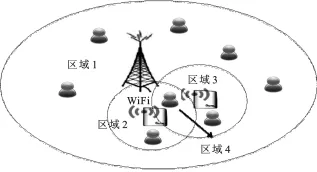
图1 异构网络场景
由于不考虑切换,所以忽略网络的预留带宽,假设每个接入网都会把网内的所有资源分配出去,也就是说,如果网络中只有1个用户,网络会把所有资源都给这个用户使用.当有新用户到达时,新老用户会竞争整个网络的资源,每个用户实际分配的带宽用bi表示,可利用非合作博弈来对这个竞争过程进行建模.
现在进行非合作博弈的建模:博弈参与者为新用户和老用户.老用户是指已经接入网络的用户,新用户是指还未接入网络的用户所有的用户用u表示
策略:老用户让出的带宽,用xi表示.新用户从老用户手中抢到的带宽,用αi表示.假设网络中已有n个用户{u1,…,un},新到达用户为un+1,对于老用户,定义支付函数如下:



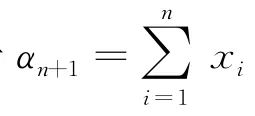
只要让所有的偏导等于0,则可以得到如下方程组:

方程组式(3)的解就是优化问题式(2)的最优解.
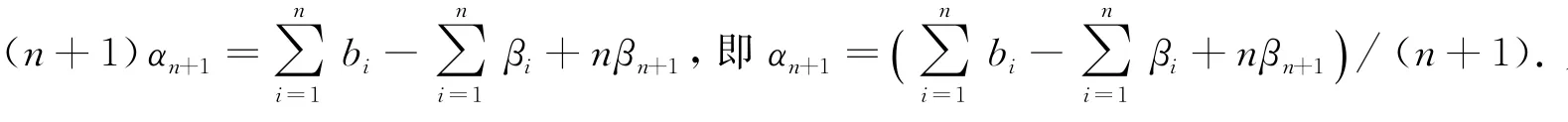
下面介绍文中提出的博弈方案的纳什均衡点,并证明这个纳什均衡点同时也是式(2)的最优解.
这里使用最佳响应函数的方法来求纳什均衡点[7].具体方法为:对所有老用户的支付函数求导,使其等于0,然后联立求解.
2 剩余服务时间的引入和算法的稳定性分析
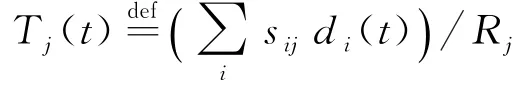
剩余服务时间表示网络随时间的推移其忙碌情况的变化.若只看带宽,一个网络中有很多需要大带宽的用户,导致新用户到达时,可以分出的带宽很小.但是,这些用户可能很快会结束业务离开网络.使用剩余服务时间,可以使新用户选择更适合的接入网.下面给出加入剩余服务时间后的算法,并使用李雅普诺夫理论分析其稳定性.
第1步 新用户到达时,根据式(3)进行博弈,得到接入每个接入网j能够得到的带宽,用Bj来表示.
第2步 得到每个接入网当前时刻的剩余服务时间Tj,然后计算DiTjRj-VBj.在所有接入网中找出最小的一个DiTjRj-VBj进行接入,其中,V是常数,代表带宽的权重.文中使用带宽进行博弈,来获得当前时刻的全局最优,所以,V取值越大,最终结果越倾向于瞬时的全局最优;反之,则倾向于长时间尺度的优化,而损失当前时刻网络的收益.
第3步 新用户选择好网络后,所有用户的带宽按照式(3)的博弈结果进行分配.
下面证明,当用户的到达速率在容量域内时,文中提出的算法可以使整个网络稳定.

当用户到达时,只要自己进行一次博弈就可以得到最终的选择结果.下面给出具体的网络选择算法.
第1步 新用户到达时,对所有它可以选择的接入网分别按照式(3)进行求解,得到它接入每一个可选的接入网可获得的带宽.
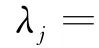
(1)容量域.假如存在一种网络选择策略,可使网络在到达率λ的情况下稳定,那么这个到达率λ就是在容量域内的,所有这样的到达率λ的集合ζ称为网络的容量域.
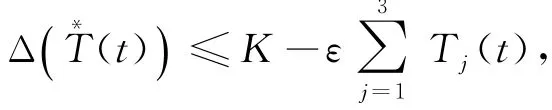
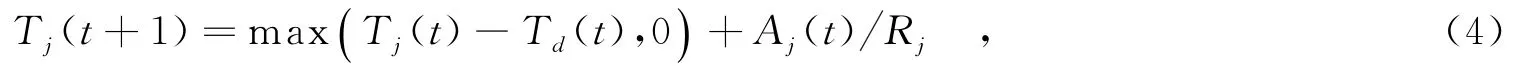
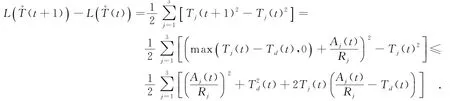
由于Aj(t)Rj和Td(t)都是有界的.所以
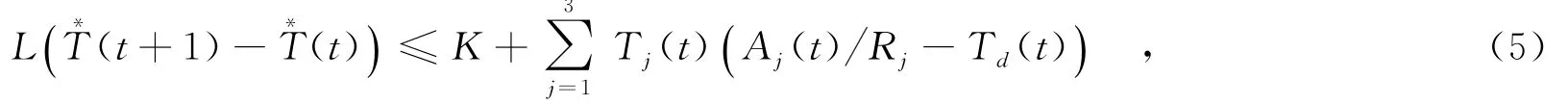
3 仿真结果
仿真的网络场景如图1所示.蜂窝网的服务速率设为10 MB/s,两个WLAN的服务速率为54 MB/s.假设业务分为两种,一种总数据量为2 MB到20 MB的均匀分布,另一种为50 MB到200 MB的均匀分布.这样假设是因为现在的移动用户的业务需求中,很少有数据量非常大的业务,其中,比较大的在线视频,在一种终端中观看1 h左右的视频,多数在200 MB以下,而用户又很少会使用移动终端看超过1 h以上的业务.用户需要的最小带宽为0.5 MB到2.0 MB的均匀分布.所有的用户按泊松过程到达整个网络.仿真中若不考虑剩余服务时间,就只需使用上文中的博弈结果进行网络选择;若考虑剩余服务时间,就使用上文中提出的加入剩余服务时间的算法.
由图2可以看出,用户的拒绝概率随着到达率的提高而提高,并且由于考虑了剩余服务时间后,用户在长时间尺度上会更加均匀地分布在整个网络中,从而降低了用户被拒绝的概率.并且能够支持更多的用户,也就是可以服务更多的数据.

图2 用户的拒绝概率随到达率的变化

图3 用户的平均收益

4 结束语
文中提出了基于非合作博弈的异构网络选择算法,并且证明了在文中的建模方法中,纳什均衡点正好也就是全局的最优点.然后,在模型中引入了剩余服务时间的概念来研究新用户对网络后续运行的影响,并且利用李雅普诺夫理论证明了在整个容量域内,笔者提出的算法可以使网络稳定.最后仿真表明,剩余服务时间的引入降低了用户的拒绝概率,并且提高了用户的平均收益.这是因为考虑了网络选择在长时间尺度上的影响,使得用户更加均匀地分布在了整个网络中.
[1]GUSTAFSSON E,JONSSON A.Always Best Connected[J].IEEE Wireless Communications,2003,10(1):49-55.
[2]宋建锋,李建东.性价比最大化的异构网络博弈选择策略[J].西安电子科技大学学报,2014,41(1):18-22. SONG Jianfeng,LI Jiandong.Gaming Network Selection Scheme Considering Performance-price Ratio Maximization in Heterogeneous Wireless Networks[J].Journal of Xidian University,2014,41(1):18-22.
[3]WANG L,KUO G S G S.Mathematical Modeling for Network Selection in Heterogeneous Wireless Networks—a Tutorial[J].IEEE Communications Surveys&Tutorials,2013,15(1):271-292.
[4]HOU J,O’BRIEN D.Vertical Handover-decision-making Algorithm Using Fuzzy Logic for the Integrated Radio-and-OW System[J].IEEE Transactions on Wireless Communications,2006,5(1):176-185.
[5]CHEN Q B,ZHOU W G,CHAI R,et al.Game-theoretic Approach for Pricing Strategy and Network Selection in Heterogeneous Wireless Networks[J].IET Communications,2011,5(5):676-682.
[6]LAHBY M,CHERKAOUI L,ADIB A.Network Selection Algorithm Based on Diff-AHP and TOPSIS in Heterogeneous Wireless Networks[C]//Proceedings of the International Conference on Multimedia Computing and Systems.Piscataway: IEEE,2012:485-490.
[7]NIYATO D,HOSSAIN E.Dynamics of Network Selection in Heterogeneous Wireless Networks:an Evolutionary Game Approach[J].IEEE Transactions on Vehicular Technology,2009,58(4):2008-2017.
[8]CHARILAS D E,PANAGOPOULOS A D.A Survey on Game Theory Applications in Wireless Networks[J].Computer Networks,2010,54(18):3421-3430.
[9]NEELY M J.Stochastic Network Optimization with Application to Communication and Queueing Systems[M]. California:Morgan&Claypool,2010.
[10]URGAONKAR R,KOZAT U C,IGARASHI K,et al.Dynamic Resource Allocation and Power Management in Virtualized Data Centers[C]//Proceedings of the IEEE Network Operations and Management Symposium.Piscataway: IEEE Computer Society,2010:479-486.
(编辑:齐淑娟)
Network selection algorithm in heterogeneous wireless networks based on residual service time
DU Bai,LI Hongyan
(State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China)
We propose a network selection algorithm based on the residual service time for the network selection problem in heterogeneous networks.There have been already many research works and achievements in this area,but most of the existing works just consider the optimal user or network revenue which does not consider the impact of new users.This paper presents the concept of the residual service time,and uses it to model the impact of the new users,in order to get a better network option on long time scales.In this paper,we use the noncooperative game to model the network,and prove that the Nash equilibrium of the model is also the global optimal solution.Finally,we use the Lyapunov stability theory to show that the proposed algorithm is stable. Simulation results show that the introduction of the residual service time can improve the network performance,reduce the blocking rate,and increase the total network revenue.
heterogeneous networks;network selection;non-cooperative game;Lyapunov;residual service time
10.3969/j.issn.1001-2400.2016.01.002
TN929.5
A
1001-2400(2016)01-0007-05
2014-08-20 网络出版时间:2015-04-14
国家自然科学基金资助项目(91338115,61231008);国家科技重大专项资助项目(2011ZX03005-004,2011ZX03004-003,2013ZX03004007-003,2011ZX03005-003);陕西省13115科技创新工程资助项目(2010ZDKG-26);国家重点基础研究发展计划资助项目(2009CB320404);国家重点实验室基金资助项目(ISN1002005,ISN090305);长江学者和创新团队发展计划资助项目(IRT0852)
杜 白(1986-),男,西安电子科技大学博士研究生,E-mail:du198614@163.com.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20150414.2046.002.html

