MIMO雷达迭代降维稳健波束形成方法
虞泓波,冯大政,解 虎
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
MIMO雷达迭代降维稳健波束形成方法
虞泓波,冯大政,解 虎
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
针对多输入多输出雷达发射、接收导向矢量失配问题,提出一种迭代降维稳健波束形成方法.首先将整体线性联合估计方法应用到多输入多输出雷达模型中,得到改进的协方差矩阵估计;接着建立多输入多输出雷达发射、接收导向矢量失配模型,根据目标信号输出功率最大原理,建立代价函数以估计真实的发射与接收导向矢量.并提出一种双迭代算法求解该代价函数,每次迭代过程仅需要求解两个低维的凸二次约束二次规划问题.仿真实验表明,与传统算法相比,在导向矢量失配严重情形下,所提算法能够取得更高的输出信干噪比,且收敛速度快,具有较低的计算复杂度.
多输入多输出雷达;稳健波束形成;二次约束二次规划;双迭代;降维
多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达能够利用多个发射天线发射正交波形,利用MIMO雷达的波形多样性可以增加系统自由度,从而提高系统干扰抑制能力、空间分辨率、参数可辨识性及目标检测能力[1-2].近年来,人们研究了稳健的波束形成方法,以提高在实际应用中最小方差无畸变响应(Minimum Variance Distortionless Response,MVDR)波束形成器[3-11]的性能.文献[3]提出了基于最坏情况的稳健自适应波束形成方法,在文献[3]的基础上又提出基于概率约束的稳健自适应波束形成方法[4].文献[5]提出基于干扰和噪声协方差矩阵重构的方法.文献[6]提出直接根据采样数据自适应计算对角加载水平的稳健波束形成方法,该方法用整体线性联合(General Linear Combined,GLC)估计的协方差矩阵代替采样协方差矩阵,以提高传统MVDR波束形成器的性能.文献[7-10]研究了利用阵列几何结构少部分先验信息进行导向矢量估计的方法,文献[7-8]说明了此类方法的参数(先验信息)依赖性低于之前的稳健波束形成方法.文献[11]提出了一种迭代求解的MIMO雷达稳健波束形成方法.
MIMO雷达系统自由度为发射阵维数与接收阵维数之积,对MIMO雷达进行全维处理,需要更多的训练样本估计协方差矩阵以提高MVDR波束形成器的性能,且涉及到的计算复杂度很高,不利于工程应用.笔者在文献[7,9]的基础上,利用MIMO雷达收发阵列少部分先验知识,根据输出功率最大原理,建立代价函数以估计真实的导向矢量,目标函数将假定导向矢量与真实导向矢量间的失配量限定在假定导向矢量的正交补空间中,并提出一种双迭代(Bi-Iteration,BI)算法求解该目标函数,以减小计算复杂度.
1 MIMO雷达稳健波束形成方法
假设一个MIMO雷达系统包含M个发射正交信号的发射阵元,N个接收阵元,θi为远场点目标的波达角,b(θi)∈CN×1,b(θi)表示接收导向矢量,a(θi)∈CM×1,a(θi)表示发射导向矢量,则MIMO雷达数据矢量可以表示为

其中,βi为回波幅度,P为信号源个数,符号⊗表示Kronecker积,z为零均值复高斯白噪声矢量.数据协方差矩阵R=E{yyH},在实际应用中通常由采样数据的最大似然估计得到:为样本数.容易求得采样矩阵求逆(Sampling Matrix Inversion,SMI)算法目标信号输出功率为

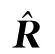
1.1发射、接收导向矢量失配模型
假设a(θt)与b(θt)分别为假定的发射导向矢量与接收导向矢量,则c(θt)=a(θt)⊗b(θt),为假定的收发联合导向矢量.为简化表示,下文中用at表示a(θt),用bt表示b(θt),用ct表示c(θt).假设ea和eb分别为发射导向矢量与接收导向矢量的失配量(这里的失配量ea与eb包含了由角度失配、阵元误差等各种因素导致的导向矢量失配),则真实的收发联合导向矢量为

由式(3)容易得到收发联合导向矢量的失配量为

1.2改进的协方差矩阵估计
文献[6]提出了应用于传统相控阵雷达的GLC方法用来估计相控阵雷达的协方差矩阵,首先将此方法拓展至MIMO雷达中,得到一个比传统采样协方差矩阵更为有效的协方差矩阵估计.由文献[6]所示,一个更为精确的协方差矩阵估计可表示为


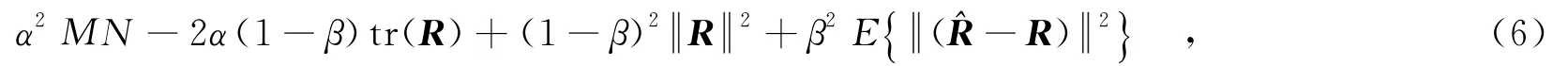
其中,

由此,一个更为精确的MIMO雷达协方差矩阵估计值为

1.3MlMO雷达稳健波束形成方法
式(3)给出了真实的发射导向矢量与接收导向矢量模型,结合式(2)可得到真实导向矢量下的MVDR波束形成器的目标信号输出功率为
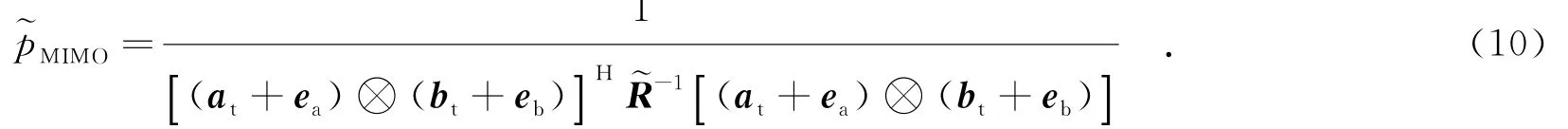

图1 函数值f(θ)随角度的变化曲线
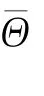
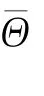
类似于文献[7]中的方法,MIMO雷达的发射阵列与接收阵列可看成两个相控阵模型进行处理,对于MIMO雷达发射与接收导向矢量,需要增加如下约束,以保证估计的导向矢量对应的角度在角域Θ内,即
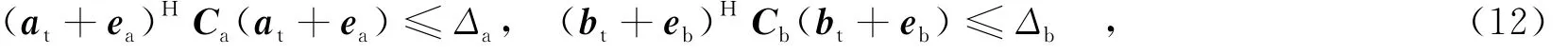
其中,
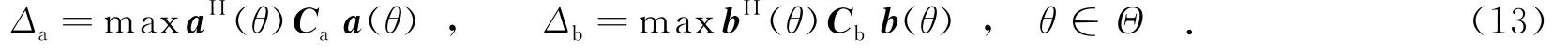
由图1可以看出,Δa与Δb的取值一定位于角域Θ的边界点上,因此,Δa与Δb取值的一个简单计算为
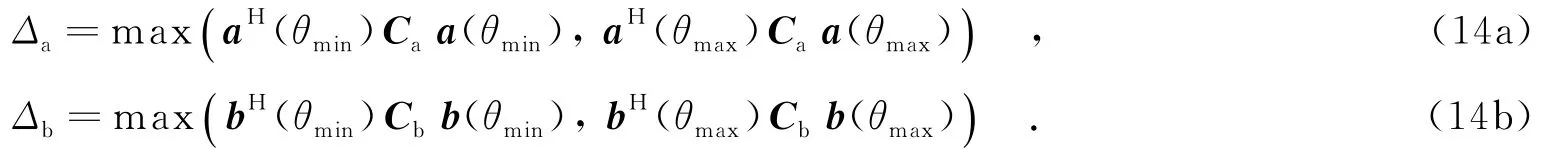
为避免(at+ea)与(bt+eb)分别收敛于零向量0a与0b,类似于文献[9]的方法,分别将失配量ea与eb进一步分解成两部分,e⊥a表示与at正交的部分,e⊥b表示与bt正交的部分,e∥a表示与at平行的部分,e∥b表示与bt平行的部分,即有ea=e⊥a+e∥a,eb=e⊥b+e∥b.需要说明的是,e∥a=γaat,e∥b=γbbt,其中γa与γb为尺度因子,故e∥a与e∥b不会影响波束形成器的输出信干噪比(Signal to Interference and Noise Ratio,SINR)[9].综上,MIMO雷达估计发射和接收导向矢量的代价函数可表示为
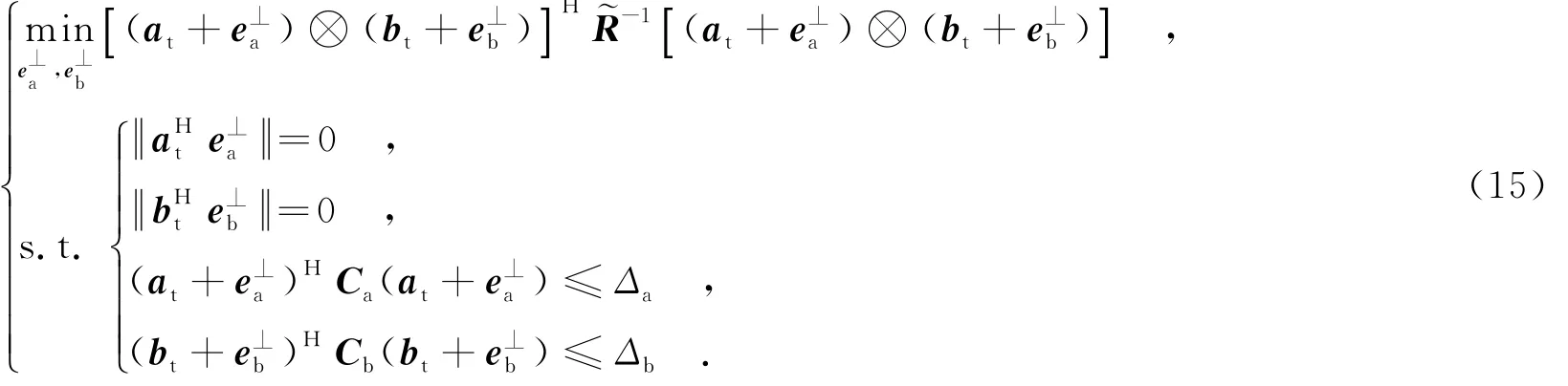
由于不容易直接求解该代价函数,笔者提出了一种双迭代二次约束二次规划(Bi-Iteration-Quadratically Constrained Quadratic Programming,BI-QCQP)算法来求解式(15)所示代价函数的最优解.
1.4Bl-QCQP算法
首先,固定e⊥a,注意到

其中,IN为N阶单位矩阵.式(15)可转化为

其次,固定eb⊥,利用式(17)所示问题是一个凸的QCQP问题,利用凸优化
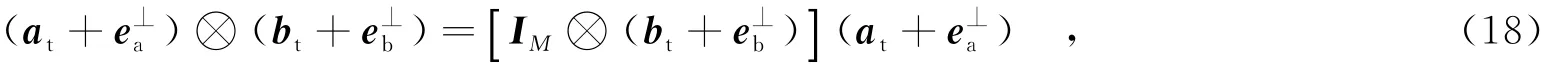
其中,IM为M阶单位矩阵.可将式(15)转化为

综上,用双迭代算法求解代价函数式(15)的BI-QCQP算法流程如下:
(1)给定初值e⊥a(0),参数0<δ≪1.
(2)将e⊥a(k-1)代入式(17)所示代价函数,求解该凸QCQP问题的最优解,得到e⊥b(k-1).
(3)将e⊥b(k-1)代入式(19)所示代价函数,求解该凸QCQP问题的最优解,得到e⊥a(k).
说明:由于BI算法的收敛性与初值无关[11],因此为方便计算,可赋初值e⊥a(0)=at.
2 仿真实验与性能分析
假设MIMO雷达系统采用收发共置的均匀线阵,阵元个数为10,阵元间距为半个波长.空间远场处存在两个点干扰,分别位于30°与50°,干噪比(Interference and Noise Ratio,INR)均为30 dB.为验证文中算法在导向矢量失配较大的场景下的性能,设假定的目标方向为3°,而真实的目标方向为6°,即目标波达方向存在3°的失配,阵元幅相误差服从零均值复高斯分布,方差为0.04.仿真实验添加5种算法与文中算法进行性能对比:文献[6]的GLC算法、文献[9]的基于协方差矩阵重构与导向矢量估计(Rec)算法、最坏情况性能最优算法(Worst-Case)[3]、基于概率约束算法(Probability Constraint,PC)[4]和经典的对角加载算法(Loaded Sample Matrix Inverse,LSMI).其中,Worst-Case算法中误差界选取ε=7;PC算法中误差界选取εpc=7,概率值选取p=0.99;LSMI方法中对角加载水平采用10σ2,σ2为噪声功率;BI-QCQP算法角域范围选取Θ=[θt-5°,θt+5°]=[-2°,8°].图4为单次实验的结果,其余为100次独立重复实验取平均值的结果.
图2给出了样本数为200时,6种算法输出SINR随输入信噪比(Signal Noise Ratio,SNR)的变化曲线图.从图2可以看出,在整个输入SNR范围内,所提算法均取得了最高输出SINR.GLC算法由于采用自适应对角加载技术,相对于固定对角加载技术LSMI显示出较好的性能.由于Rec算法首先使用Capon谱进行协方差矩阵重构,而Capon法对阵元福相误差较为敏感,在阵元幅相误差较大时重构后的协方差矩阵与理想协方差矩阵偏差较大,Rec算法性能会严重下降[10].
图3给出了SNR为-5 dB时,6种算法输出SINR随样本数变化曲线,样本数从10开始,在样本数小于100时,为保证Worst-Case、PC、Rec算法的协方差矩阵可逆,对这3种算法的协方差矩阵进行对角加载,加载因子为10σ2.从图3可以看出,与其他4种算法相比,所提算法的输出SINR在整个样本数范围均获得了最大值,所提算法与Worst-Case、PC、Rec、LSMI算法在样本数为200以后开始收敛,而GLC算法随着样本数的增加性能逐渐下降,这是因为当样本数较大时估计的协方差矩阵更接近理想协方差矩阵,从而由自适应对角加载技术得到的对角加载水平减小,不能提供足够好的抗导向矢量失配的稳健性.

图2 输出SINR随SNR变化曲线

图3 输出SINR随样本数的变化曲线

图4 输出SINR随迭代次数的变化曲线
图4给出了SNR为-5 dB时,BI-QCQP算法输出SINR随迭代次数的变化曲线,从图4可以看出,经过3 ~4步文中算法开始收敛,说明BI-QCQP算法可快速收敛.BI-QCQP算法每一步迭代过程仅需要分别求解两个低维QCQP问题,因此,BI-QCQP算法的快速收敛性就使得所提算法具有较低的计算复杂度.
下面详细分析6种算法的计算复杂度,忽略低阶项(二阶及以下项),其中,Worst-Case算法与PC算法中均需求解二阶锥规划问题(Second-Order Cone Programming,SOCP),用内点法容易求解,一般在10步左右可以收敛[3],Rec算法与文中BI-QCQP算法均需要求解QCQP问题,用内点法求解其迭代次数一般也需要10步左右.因此,可以假设上述4种算法中每一次用内点法求解SOCP或QCQP问题的迭代次数均为B=10(实际中每次求解的迭代次数可能不同,但一般均在10次左右),以便于对计算复杂度进行分析.BIQCQP算法的迭代次数假设为3步.
表1列出了6种算法的计算复杂度.BI-QCQP算法由于采用迭代降维处理,每次迭代只需分别求解两个低维的QCQP问题,且算法可以快速收敛,而Worst-Case算法、PC算法及Rec算法均需进行全维迭代处理,因此与Worst-Case算法、PC算法及Rec算法相比,其计算复杂度更低.此外,在进行权矢量更新时,BIQCQP算法的计算复杂度为(O 3B(M3+N3)),远小于Worst-Case算法、PC算法及Rec算法的计算复杂度O(BM3N3),从而较大提高了计算效率.

表1 6种算法计算复杂度比较
3 结束语
笔者将GLC算法应用到MIMO雷达模型,得到改进的协方差矩阵估计,接着利用MIMO雷达收发阵列少部分先验知识,根据目标信号输出功率最大原理建立代价函数以估计真实的发射与接收导向矢量.用BI算法求解该代价函数,将原始的高维问题转化为低维的凸QCQP问题.仿真实验表明,与传统算法相比,在导向矢量失配严重的情形下,文中算法能够取得最高的输出SINR,且能快速收敛,与其他稳健波束形成算法相比,具有较低的计算复杂度,尤其在进行权矢量更新时,能够较大提高计算效率.
[1]HAIMOVICH A M,BLUM R S,CIMINI J,et al.MIMO Radar with Widely Separated Antennas[J].IEEE Signal Processing Magazine,2008,25(1):116-129.
[2]王旭,周生华,刘宏伟,等.一种空时联合优化的MIMO雷达波形设计方法[J].西安电子科技大学学报,2014,41 (3):42-48. WANG Xu,ZHOU Shenghua,LIU Hongwei,et al.Waveform Design Method for MIMO Radar Based on Joint Spatial and Temporal Optimization[J].Journal of Xidian University,2014,41(3):42-48.
[3]VOROBYOV S A,GERSHMAN A B,LUO Z Q.Robust Adaptive Beamforming Using Worst-Case Performance Optimization:a Solution to the Signal Mismatch Problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.
[4]VOROBYOV S A,CHEN H,GERSHMAN B.On the Relationship between Robust Minimum Variance Beamformers with Probabilistic and Worst-Case Distortionless Response of Constraints[J].IEEE Transactions on Signal Processing,2008,56(11):5719-5724.
[5]GU Y,GOODMAN N A,HONG S H,et al.Robust Adaptive Beamforming Based on Interference Covariance Matrix Sparse Reconstruction[J].Signal Processing,2014,96(B):375-381.
[6]DU L,LI J,STOICA P.Fully Automatic Computation of Diagonal Loading Levels for Robust Adaptive Beamforming [J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):449-458.
[7]KHABBAZIBASMENJ A,VOROBYOV S A,ABOULNASR H.Robust Adaptive Beamforming Based on Steering Vector Estimation with as Little as Possible Prior Information[J].IEEE Transactions on Signal Processing,2012,60 (6):2974-2978.
[8]VOROBYOV S A.Principles of Minimum Variance Robust Adaptive Beamforming Design[J].Signal Processing,2013,93(12):3264-3277.
[9]GU Y,LESHEM A.Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885.
[10]GONG C,HUANG L,XU D,et al.Knowledge-aided Robust Adaptive Beamforming with Small Snapshots[J]. Electronics Letters,2013,49(20):1258-1259.
[11]ZHANG W,WANG J,WU S.Robust Minimum Variance Multiple-Input Multiple-Output Radar Beamformer[J].IET Signal Processing,2013,7(9):854-862.
(编辑:齐淑娟)
Iterative dimension-reduced robust adaptive beamformer for MIMO radar
YU Hongbo,FENG Dazheng,XIE Hu
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)
Aiming at the transmitted and received steering vectors mismatch problem,an iterative dimension-reducing robust adaptive beamformer for MIMO radar is presented.The General Linear Combined(GLC)method is applied in MIMO radar to obtain the enhanced covariance matrix estimation,and the transmitted and received steering vectors mismatch model is established.The cost function is established based on the desired signal output power maximum principle to estimate the transmitted and received steering vectors.The bi-iteration method is proposed to solve the cost function and it is merely necessary to find out two low-dimensional convex quadratically constrained quadratic programming(QCQP)problems in per iteration.Simulation results show that the proposed method can obtain the higher output signal-to-noise-plus-interference(SINR)under the condition of severe steering vector mismatch than the conventional robust beamformers,and that the proposed method can converge fast so that it has the lower computational complexity.
multiple-input multiple-output(MIMO)radar;robust beamformer;quadratically constrained quadratic programming(QCQP);bi-iteration;dimension-reduced
TN958.92
A
1001-2400(2016)01-0030-06
10.3969/j.issn.1001-2400.2016.01.006
2014-07-20 网络出版时间:2015-04-14
国家自然科学基金资助项目(61271293)
虞泓波(1988-),男,西安电子科技大学博士研究生,E-mail:beyond̠hongbo@126.com.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20150414.2046.022.html

