例析分段函数中的热点题型

☉江苏省如皋市第二中学 郝红云

例析分段函数中的热点题型

☉江苏省如皋市第二中学 郝红云

所谓“分段函数”是指在函数定义域内，自变量x的区间分为多段，不同的区间对应不同的法则，具有这种特点的函数叫作分段函数.分段函数的求解中，首先不要把它误认为是几个函数来进行求解；分段函数的书写，与其他函数有所区分，在书写时使用花括号，将各段函数采用上下并排的方式并列写在一起，并注明各段函数的自变量x的取值范围.分段函数的定义域是各段函数的定义域的并集，实际是求解连续的区间的定义域.值域的求解与定义域相似.分段函数的图像首先对函数的自变量进行分析，确定自变量的区间，按照相应的区间，分段画出函数的图像；分段函数的函数值求解的过程中，首先也要对函数的自变量进行分析，确定自变量的区间，然后探究这一区间函数的表达式，按照表达式进行函数值的求解，直至求解出函数值，完成分段函数的求解.

分段函数是近几年高考的热点内容，涉及求分段函数的函数值、最值、奇偶性、单调性等问题，解答这些问题中渗透了分类讨论、数形结合等多种数学思想方法.笔者结合平时的教学实践，谈谈分段函数中的热点题型.

题型一——作出分段函数的图像

此类题型就是根据分段函数的解析式作出每段上的图像，有的可以考虑图像变换得到.

例1 作出y=|x2-2x-3|和y=x2-2|x|-3的图像，并说明这两个图像可由y=x2-2x-3的图像经过怎样的变换得到.

解析：在不同的平面直角坐标系下，分别作出y=|x2-2x-3|与y=x2-2|x|-3的图像.

事实上，y=|x2-2x-3|=可分段画出图像，如图1、图2所示.

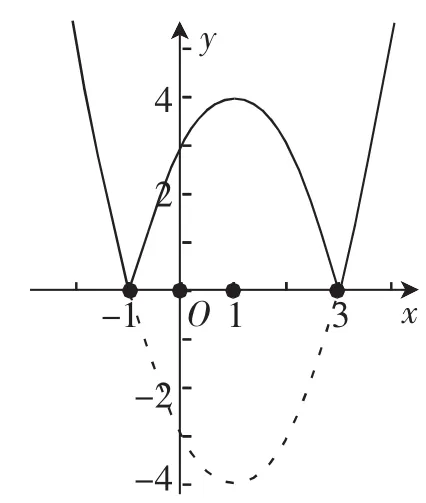
图1

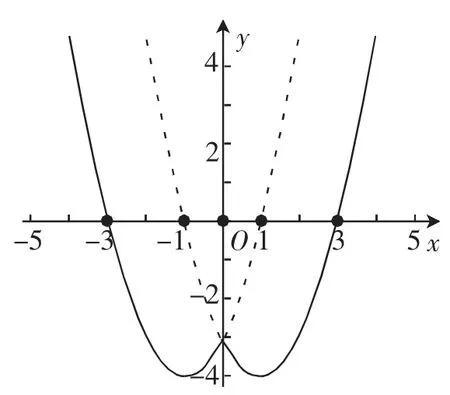
图2

通过观察图像可知，y=|x2-2x-3|的图像可由y=x2-2x-3的图像经过下列变换得到：保持y=x2-2x-3的图像在x轴上方的部分不变，x轴下方的图像沿x轴翻折上去即可.y=x2-2|x|-3的图像可由y=x2-2x-3的图像经过下列变换得到：保持y=x2-2x-3的图像在y轴右侧的部分不变，原左侧的图像换成将y轴右边的图像沿y轴翻折而成的图像即可.

思考：对于一般的函数y=f（x），如何通过变换得到y=|f（x）|及y=f（|x|）的图像？方法是类似的.

点评：分段函数有几段，其图像就由几条曲线组成，作图的关键是根据定义域的不同，分别由表达式作出其图像.作图时，一要注意每段自变量的取值范围；二要注意间断函数的图像中每段的端点的虚实.

题型二——求分段函数中参数的范围

分段函数的参数的取值范围的求解，首先分析自变量所处的区间，然后根据所在定义域代入相应的解析式，画出相应的图像，再根据数形结合去解.

解析：当x＞0时，（fx）=（fx-1），即当x＞0时，（fx）的图像与（fx-1）的图像相同，而（fx-1）的图像可由（fx）的图像向右平移1个单位得到，可先作出（fx）在x≤0时的图像，如图3；再将它向右平移1个单位，如图4；取（fx-1）在x＞0时的图像即能得到（fx）在（0，1］上的图像，如图5.

图3

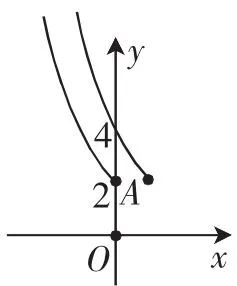
图4

图5

重复上面图像平移、选取的步骤就可得到f（x）在x＞0的图像，如图6.

图6

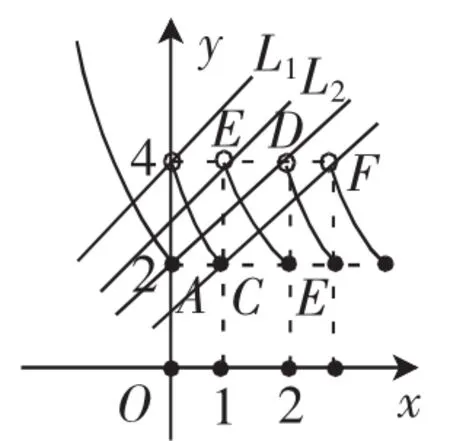
图7

方程f（x）=x+a有且只有两个不相等的实数根，可转化为函数f（x）的图像与直线y=x+a有且只有两个不同的交点.观察图像发现直线AD、CF的斜率为1，通过直线平移观察可得，只有当直线y=x+a在直线L1与L2之间运动时才满足要求，如图7，从而可得3≤a＜4.

点评：此类分段函数的特点是一段是具体函数，另一段反映图像变换.由图像变换来获得图像，一般要经历图像变换和图像选取两个步骤.本题中当x＞0时f（x）= f（x-1），由作图可知，f（x）在（-1，+∞）上是周期为1的周期函数.

题型三——求分段函数的定义域和值域

文章对定义域与值域的概念进行解析.在进行分段函数定义域与值域的求解时，需画出函数图像，通过清晰的图像来理清思路，利用数形结合的思想进行解题.

函数的定义域与值域的求解方法相似，在进行求解的过程中，都要考虑自变量x的区间范围，定义域是在分段函数求解后，将求解的数值取并集，值域同上.分段函数的值域的求解是近年来的高考热点.

解析：作出函数图像，如图8所示.利用“数形结合”易知f（x）的定义域为［-1，+∞），值域为（-1，3］.

点评：在分段函数的定义域与值域求解中，主要是分析各段函数共同拥有的区间，根据共有的区间进行求解.

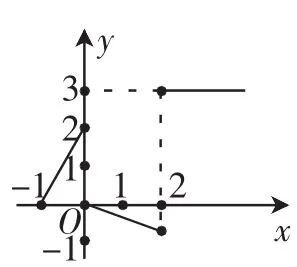
图8

题型四——求分段函数的解析式

求函数解析式遵循“求谁设谁”的原则，首先要设置自变量的区间，求哪个区间的解析式，自变量x就设在哪个区间内，然后代入已知区间的解析式，利用奇偶性解出f（x）.

解析：设x＜0，则-x＞0.

因为（fx）是偶函数，

点评：求分段函数的解析式时，分别求出定义域内各段对应的解析式，将所求的定义域内的函数解析式组合在一起，完成分段函数解析式的求解.在进行求解的过程中，注意自变量的设置情况，遵循“求谁设谁”的原则，还有注意考虑所有的区间，保证求解解析式时，不会出现错漏的状况.

题型五——分段函数的单调性判断

分段函数单调性的判断方法：分别求出各段函数在其定义区间内的单调性，多个区间用“，”相连.仍可借助图像判断其单调区间，体会数形结合的思想.

例5 写出函数（fx）=|1+2x|+|2-x|的单调区间.

当x≥2时，（fx）=（1+2x）+［-（2-x）］=3x-1；

图9

点评：分段函数的单调性的判断是高考数学中的重要考点，学生在学习的过程中必须掌握判断方法.判断分段函数的单调性时，首先对各段的分函数的性质进行判断，然后根据各段函数的情况，来判断区间分界点函数值的关系，确定分段函数的单调性.假若每一段函数单调性一致，分界点处函数值一致，说明分段函数符合单调性性质，则在整个定义域上单调递增或递减，反之，不符合单调性的定义，则说明函数的单调性不一致，就要对各段函数分段说明其单调性.

题型六——分段函数中的不等式问题

分段函数中通常会涉及不等式问题，解决此类问题也是分段讨论，得到相应的解析式，列出不等式求解.

解析：在（f（fx））≤3中，令（fx）=t⇒（ft）≤3.由（ft）≤3

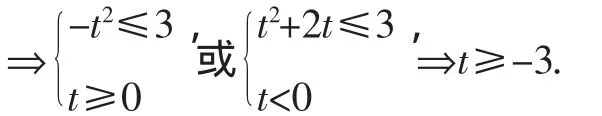
点评：分段函数与不等式是高考的常考点，难度不大，尤其是在解不等式时又伴随着参数，在求解这类问题时，注意应用分类讨论和数形结合这两个思想，使不等式的求解过程简化.

题型七——分段函数中方程和零点的问题

这类题型一般考查函数与方程、数形结合的数学思想.

例7 已知（fx）是定义在［1，+∞）上的函数，且（fx）=则函数y=2x（fx）-3在区间（1，2015）上零点的个数为___________.

解法一：由例1可知，先作出（fx）在1≤x＜2上的图像，再将它的横坐标伸长原来的2倍，纵坐标变为原来的一半，再选取x≥2的部分，可得（fx）在2≤x＜4上的图像.如此反复，可得（fx）在x≥2的图像，如图10.

图10

函数y=2x（fx）-3在区间（1，2015）上零点的个数可转化为方程（fx）=的根的个数，进一步可转化为函数y=（fx）与y=的图像在（1，2015）上交点的个数，如图11.

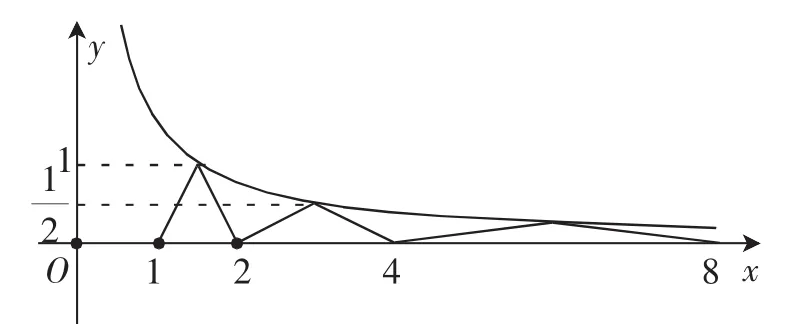
图11

P切PQ而线段PQ与函数y=的图像只有一个交点，由一般性可知在图像变换的每一段上两个图像只有一个交点.

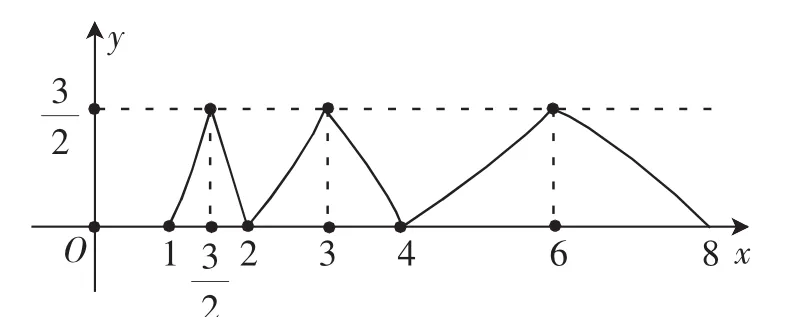
图12

函数y=2x（fx）-3在区间（1，2015）上零点的个数可转化为方程g（x）=的根的个数，进一步可转化为函数y= g（x）与y=图像在（1，2015）上交点的个数.结合上述图像易得，函数y=2x（fx）-3的零点为x=，令，所以函数y=2xf（x）-3在区间（1，2015）上零点的个数是11.

点评：解法一与解法二对比可知，解法二明显更符合命题者的意图，更易操作，而解法一操作时由图像不能直接判断交点的个数，此时需从代数角度寻求解决方案.方程的根与函数的零点是一一对应的，在新课标教材中，这是一个基础的知识点，其中含参问题更是高考热点.

题型八——分段函数中的应用问题

例8 如图13，动点P从边长为1的正方形ABCD的顶点A处出发顺次经过B，C，D再回到A，设x表示P点的行程，y表示PA的长度，求y关于x的表达式.

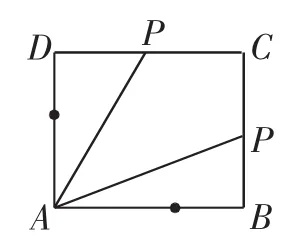
图13

解析：如图13所示，当P点在AB上运动时，PA=x；

当P点在CD上运动时，由Rt△PDA求出PA=

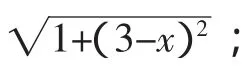
当P点在DA上运动时，PA=4-x.

点评：前段对高考分段函数中的各个考查重点进行讨论，这里探讨实际问题中分段函数的模型，应该了解这也属于高考数学考查分段函数的重点.

分段函数作为高考的热点，学生在学习时应该加强注意力.同时分段函数作为练习和模拟题中的常客，其涉及多方面的内容，在进行每部分内容的学习时，根据内容的特点，来具体学习.学习中要综合运用分类讨论思想、数形结合思想、化归转化思想、方程与函数思想、建模思想，才能让问题迎刃而解，事半功倍.通过以上各类题型的分析，不难得到分段函数在考查中的一种解题的重要途径是：函数图形会使分段函数的求解过程更加清晰化，在分段函数相关内容的学习时，坚持数形，将分段函数明显地表现在图像中，再结合等价转化思想、分类讨论等函数思想求解分段函数，提升学习的效果.