立足起始课教学，培养核心素养——对数概念教学的实录与反思

☉江苏省苏州第十中学校 毛东良

立足起始课教学，培养核心素养
——对数概念教学的实录与反思

☉江苏省苏州第十中学校 毛东良

一、背景

数学核心素养，从通俗的角度来讲，就是把所学的数学知识排除或忘掉后剩下的东西，能从数学的角度看问题，有条理地进行理性思维、严密求证、逻辑推理的意识和能力.从专业的角度讲，就是主动探寻并善于抓住数学问题的背景和本质的素养；熟练地运用准确、简明、规范的数学语言表达自己的数学思想.本文试着从教学过程的维度，通过对数概念这节起始课，思考数学核心素养的培养.该课是笔者参加2015苏州大市评优课所开设的一节公开课.

二、教材解读

“对数的概念”是苏教版教材必修1“对数函数”的起始课，是前面指数概念和指数函数的回顾、深化和延续，同时又是学习对数运算性质和对数函数的基础.指数运算是已知底数和指数求幂值，而对数则是已知底数和幂值反过来求指数，对数既是一种全新的运算，又起到承上启下的作用.

三、教学过程

（一）概念的生成在情境中引发

情景1计算：

（1）16×256=_______；

（2）256×4096=______；

（3）4096×32768=______.

师：请大家以最快的速度完成上面3个计算.

生1：第（1）问我发现一个规律，如图1，

16×256=24×28=24+8.后面的数字太大还在计算中.

师：很棒，有没有办法快速处理（2），（3）这类大数据的运算？（受到了刚才的启发，学生很快有了思路）.

生2：是不是都可以化成2的多少次方来处理呢？（教师ppt上引入图1，快速解决（2），（3））

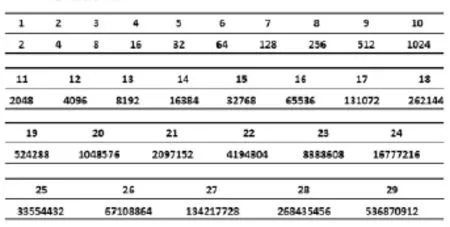
图1

师：谁能概括一下这种算法的优点？

生3：这种计算方法的优点就是把复杂的乘除运算转化成了简单的加减运算.

师：实际上二千多年前阿基米德在还没有指数运算法则的情况下就发现了这个规律，但可惜没有继续探究下去，也没有在实际生活中得以运用，失去了对数破土而出的机会.

（二）概念的感悟在观察中发现

情景2计算：299792.458×31536000=1光年

299792.458→光在真空中的速度（千米/秒）

×31536000→一年的秒数

1 光年→一个天文单位

能否利用刚才的运算处理这个大数据运算？回到表格中…

问题：31536究竟等于2的多少次方？

生4：根据y=2x与y=31536的图像，精确值肯定存在，由表格知在14与15之间，但求不出.

师：可见这一数表虽然好但不够用，无法找到满足方程2x=31536的x准确值.早在16世纪德国数学家斯蒂菲尔德，就发现了这种神奇的计算方法，但他也遇到同样的问题.许多人为了制作一张更为精确的表格而奉献了自己毕生的精力.

图2

设计意图：通过经历16，17世纪大数据的运算难题，使学生深刻认识到对数对简化运算的重大作用和引进对数的必要性，对数和指数的联系通过表格得到了初步体现.同时通过丰富的情景和动人的历史故事激发学生的求知欲和创造欲，形成锲而不舍的钻研精神和科学态度.在发现对数的过程中，同时也涉及到了对数的运算性质，为后续学习做好了铺垫.

（三）概念的构建在类比中揭示

师：回顾初中数学，为了解方程a3=2引入了新的符号根式“”，方程的解就用a=表示.类似地，请大家思考：如何得到方程2x=31536的解呢？

生5：也引进一个符号来表示这个数，而且含有2，31536这两个数.

师：不错，苏格兰数学家纳皮尔首创“log”与2，31536组成的整体log231536来表示一个2的多少次幂等于31536的数，这样的数就称为对数.引导学生将其推广到一般情形：

师：板书：若ab=N（a＞0，a≠1），则logaN=b（a＞0，a≠1）.

写法：格式四线三格，如图3.

图3

读法：以a为底，N的对数.注意不是“log”以a为底，N的对数（.请同学一起来读一下x=log0.850.5）.

师：对数式logaN=b中a和N有什么限制呢？

生6：可以从指数式来研究对数式：一个关系，两种表示.

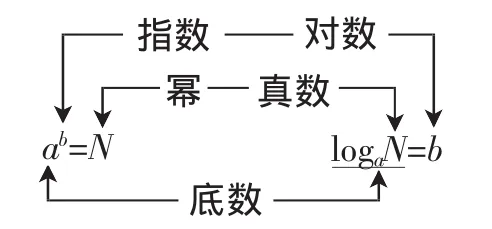
引导学生得出a＞0，a≠1和N＞0.（教师板书）

设计意图：对数符号是难点，注意书写格式，避免因书写不规范而产生的错误，强化对数符号的认识和理解.明确指数式和对数式中a，b，N是相同的，理解指数式与对数式的相互关系，互化也体现了等价转化这个重要的数学思想.

（四）概念的深化在互动中建立

活动1：每位同学书写四个对数式，写完后同桌交换检查、纠正.

活动2：将同桌书写的四个对数式改写为指数式后，再互相检查、纠正（效果相当不错）.

活动3：将下列对数式改写为指数式：（1）log10a=-1.699.（2）loge1=0（e=2.7182818284…）.（学生板演）

师：常用对数log10a=lga.纳皮尔（Napier）的对数在爱丁堡发表以后，布立格斯（Briggs，1561～1630）根据他在牛津大学讲授纳皮尔对数的经验和体会，提出了他的改进意见：建议将对数改良为以10为底的对数最为方便实用.布立格斯与荷兰数学家佛拉格（Vlacq）共同完成了1 至100000的以10为底的14位的对数表，这就有了常用对数.

自然对数logea=lna（e=2.7182818284…），很多反映自然规律的数学模型都包含e，如放射性元素的衰变公式、牛顿的冷却定律，还有化学、物理和建筑学等自然学科，所以称为自然对数.

设计意图：三个学生活动加深对数概念的理解.历史背景的介绍，让学生明白“常用对数”和“自然对数”背后曲折的故事，强化了学生对对数概念的认识，体会数学文化的传承精神.

问题1求下列各式的值：（1）log28；（2）log927.

教师巡视学生答题情况，投影交流学生的解法.

生7：由23=8，得到log28=3.

生8：设log28=x，则2x=8=23，所以x=3.

师：设x的目的是什么？

生8：将对数式转化为指数式，从而解决问题（.1）中容易得到23=8，故不需要设x；（2）问中不容易得出相应的指数式，可通过设x将对数式转化为指数式的可能性更大.设log927=x，由定义知，9x=27，即32x=33，得x=，即log27=.

9

师：在对数式不熟练时可先设x转化为指数式，确定x值，即用对数的定义去解决问题.

设计意图：帮助学生在应用的过程中进一步认识对数概念的本质，加深对对数概念的理解，掌握对数式与指数式的互化方法，培养学生的运算能力和分析问题、解决问题的能力.

师：同学们有没有发现每次不管哪个方法你都要回到指数的形式很麻烦，下面我们来看看对数的运算，我们能不能从中发现一些简单性质，方便运算.

问题2求对数的值：（1）log31；（2）log33；（3）lne；（4）log1；（5）lg1；（6）lg10；（7）ln1；（8）log0.50.5.

（以上问题解答由学生板演）

师：从问题2的结果你有什么发现？

生9：（1），（4），（5），（7）的真数均为1，可得loga1=0；（2），（3），（6），（8）真数和底数均一样，可得logaa=1.

师：能证明上述2个归纳得到的结论吗？

生10：通过指数式可证明.

问题3 求对数的值：（1）log55-2；（2）log335；（3）2log23；（4）7log70.6.

生11：由（1），（2）发现logaab=b；（3），（4）不太会处理.

生12：设log23=x，则2x=3，消掉x后发现2log23=3.同理7log70.6=0.6.

师：很好，大家能从上面的解法中猜出alogaN=N的值吗？如何证明？生齐答：N.

生13：由指数式ab=N，得对数式b=logaN，可代掉N，得到logaab=b；而代掉b，得到alogaN=N.

（师生掌声认同，教师将4个结论板书）

设计意图：通过学生讨论交流，从例题、练习中归纳、猜想、证明得到对数的简单性质，强化了数学思想方法.

（五）收获的提升在总结中升华

师：谁来小结一下我们今天数学课的收获？

生14：我们了解了对数的诞生，学习了对数的定义，以及指数式、对数式的互化.

师：对数从思想萌芽到诞生经历了漫长的200多年，通过刚才介绍的故事，同学们能受到哪些启发？

生15：人类最初为了解决繁难的大数运算不断寻求突破，从而有了对数思想的萌芽和对数的诞生，同时困难也迎刃而解，真是思路决定出路，没有创新就无法突破.

生16：纳皮尔坚持对数的研究多年，这需要怎样坚韧不拔的意志和信念.假如我能为了我的兴趣和爱好如此投入，那该会有怎样的成就呢？

生17：布里格斯为了共同的爱好去拜访纳皮尔，才有了他们的思想碰撞，使对数得到改进和完善.可见人类的交流多么重要，闭目塞听、闭门造车只会让人类的文明止步不前.

师：今天和大家沿着历史的足迹，探索了对数的含义，完成了前人用了两千年的时间探索完成的对数的概念，同时也完善了我们的运算知识体系，从中感受到了数学的玄妙.

四、教学反思

（一）情景教学，揭示概念教学规律

对数的发展史告诉我们，对数思想的起因源自实际需要.对数概念的产生从阿基米德、舒开、斯蒂费尔到纳皮尔《奇妙的对数表的说明》的问世，人类思维经历了一个由具体形象到形式抽象发展的漫长过程.就如伊夫斯所言：“在向学生讲授一门学问时，应当按照这门学问发展的顺序来进行.”让学生亲历概念形成过程；数学家对于该概念的探究活动，感知对数概念的发现历程；理解科学发现的艰难曲折的过程；体悟数学的人文精神，体验数学探究的成功喜悦感.

（二）类比归纳，破解概念教学难点

本课的教学难点是对数的定义和简单性质的发现.对数的定义采用了类比方法，类比方法是几种逻辑推理中最富有创造性的，科学史上很多重大发现、发明，往往发端于类比，类比被誉为科学活动中的“伟大引路人”.开普勒说：“我珍惜类比胜于任何别的东西，它是我最依赖的老师，它能揭示自然界的秘密，在数学中最不可忽视.”

（三）合作探究，拓展概念教学深度

高中数学新课程倡导自主探索、动手实践、合作交流等学习方式，这些方式有助于发挥学生学习的主动性，使学生的学习过程成为在教师引导下的“再发现、再创造”过程.不必将各种概念定理灌输给学生，

而应创造适当的条件，让学生加强反思同时通过自身的实践活动来主动获取知识.