把握关键，明确目标——立体几何问题求解中关键条件的确定

☉天津市南开中学 李稀琰

把握关键，明确目标
——立体几何问题求解中关键条件的确定

☉天津市南开中学 李稀琰

在某些立体几何的试题中涉及距离、面积或体积，但这样的线、面、体并没有直接给出，需要我们来构造确定.解题中若能准确利用已知条件，明确目标图形，常可使解题事半功倍.下面举例说明.

一、明确定点

例1 设正方体A—C1的棱长为1，P为面对角线AB1上的动点，Q为棱AB上的动点，求C1P+PQ的最小值.

解析：当点P在对角线AB1上的位置固定时，要使PQ最短，只要PQ⊥AB.如图1，由于C1P与PQ不共面，则需将等腰Rt△ABB1绕AB1旋转落在平面DAB1C1上，得五边形DABB1C1，如图2所示，当且仅当C1、P、Q三点共线时，C1P+PQ的值最小.

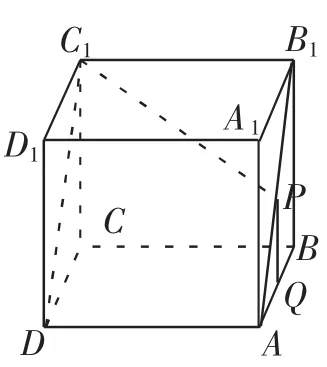
图1

作C1Q⊥AB于Q，交AB1于P点，则C1P+PQ最短.作B1E⊥C1Q 于E，得EQ=B1B=1，又C1E=B1C1· sin∠B1C1E=1·sin45°=，故C1Q=C1P+PQ=C1E+EQ=1+

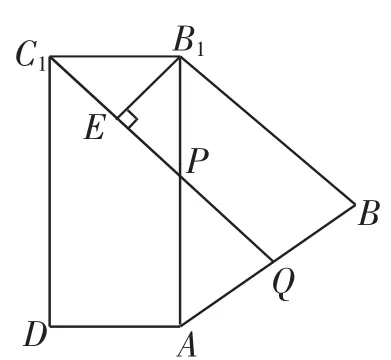
图2

评析：本题的求解关键是确定点Q的位置，将空间问题平面化后，利用三点共线原理明确点Q所在位置是问题求解的关键.柱、锥、台等多面体或旋转体的表面上的两点间的距离最短问题，通常将其沿棱或母线展开，转化成平面几何中图形性质推理求解，即“立体图形平面化”.

变式1 如图3，在侧棱长为2，底面边长为1的正四棱柱ABCD-A1B1C1D1中，P是对角线BD1上的动点，则AP+CP的最小值为_______.

解析：将△ABD1与△BCD1所在平面展开为一个平面，得到图4，则AC之长即为所求.

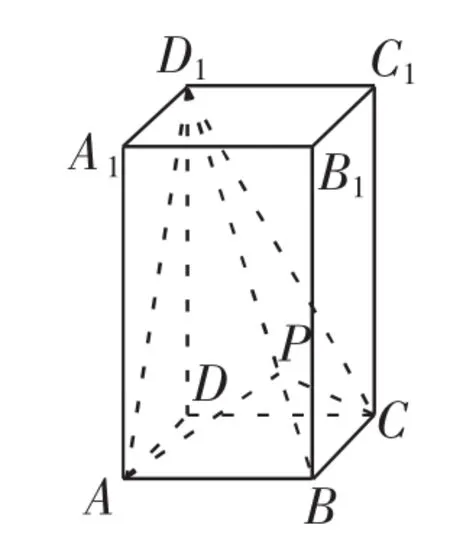
图3

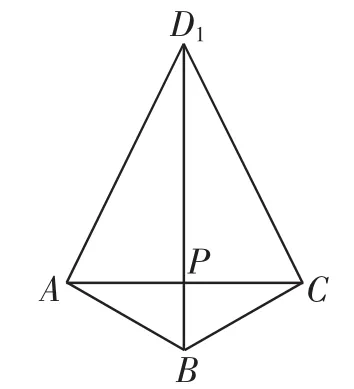
图4

因为AB=1，AA1=2，AB⊥AD1，BC⊥CD1，

所以AD1=CD1=

在Rt△AD1B中，BD1=

评析：本题不必构造目标函数来求最值，因为P是BD1上的动点，所以选对点P的位置，使A、P、C三点共线，即可使得AP+PC取得最小值，因此将有关图形展开到一个平面内求解，即空间问题平面化，这是解答相关立体几何问题的一种有效策略.

二、明确定线

在立体几何的某些试题中经常会遇到求距离的最值问题，欲求解该最值，需要我们先确定最值取得的位置，然后再利用平面几何的相关知识求解.

例2 在长方体ABCD-A1B1C1D1中，AB=，BC= AA1=1，点P为对角线AC1上的动点，点Q为底面ABCD上的动点（点P，Q可以重合），则B1P+PQ的最小值为（）.

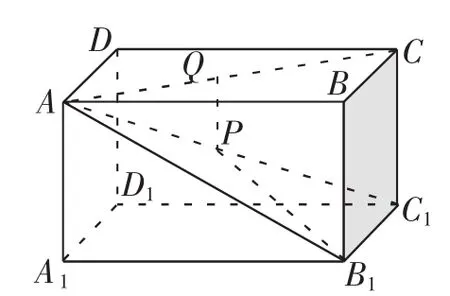
图5

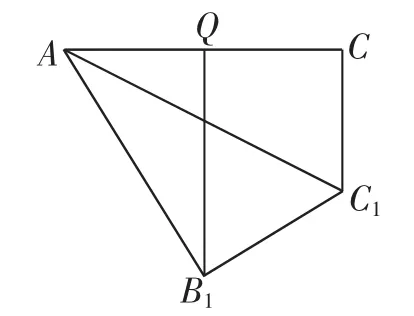
图6

解析：如图5所示，求B1P+PQ的最小值，易知当点Q位于AC上时，PQ可取到最小值.

连接AB1，将平面AB1C旋转至与平面ACC1在同一平面（如图6），过点B1作AC的垂线，交AC于点Q，则B1Q即为所求最小距离.

由由题目条件知，AC⊥CC1，AB1⊥B1C1，AB1=∠CAC1=∠B1AC1=30°，所以∠AB1Q=30°，所以AQ=由勾股定理得B1Q=，即为所求.故正确选项为C.

评析：本题将点到点的距离转化为点到面的距离，同样利用平面化策略，将问题转化为点到线的最小值问题，点到面的垂线段长即为最小值.

变式2 在边长为2的正方体ABCD—A1B1C1D1中，E 为BC的中点，点P在底面ABCD上移动，且满足B1P⊥D1E，则线段B1P的长度的最大值为（）.

解析：对于动态问题的解答要把抓住其中不变的因素，如本题中的点P为面ABCD内的动点，但B1P⊥D1E，因此B1P在一个与D1E垂直的定面上.找到这个定面即可顺利解决问题.

如图7，取CC1的中点F，连接B1F并延长交BC的延长线于点G，连接AG交CD于点H，连接AB1.

易知D1E⊥AB1，D1E⊥B1F，所以D1E⊥平面AB1G，即点P在线段AH上.

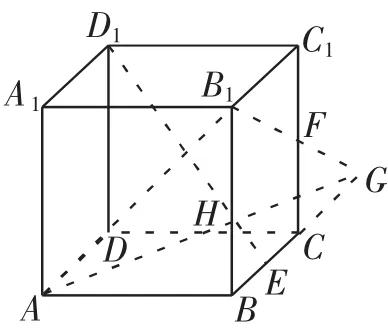
图7

又△GCF∽△GBB1，△GHC∽△GAB，所以，所以H为CD的中点.在△ABH中，易求得

1B1A=2，在△B1BH中，B1H=3，所以线段B1P的长度的最大值为3，故选D.

评析：定线与动线垂直，则动线在与定线垂直的定面内，找到这个定面即可顺利求解.类似若动线与已知面平行，则动线在与已知面平行的定面内等.只要抓住这些动态问题中的不变因素，则可找到问题的求解思路.

三、明确定面

例3 已知正方体ABCD-A1B1C1D1的棱长为2，E是棱D1C1的中点，点F在正方体内部或正方体的表面上，且EF∥平面A1BC1，则动点F的轨迹所形成的区域面积是（）.

解析：因为点E为定点，点F为动点，EF为动线，但EF∥平面A1BC1，故EF在与平面A1BC1平行的平面内，所以确定过点E且平行于平面A1BC1的定面是问题求解的关键所在.如图8所示，分别取棱A1D1，A1A，AB，BC，CC1的中点F，G，H，I，J，易知连接各中点所得六边形与平面A1BC1平行，所在点F在此六边形内.

图8

连接EG，在△EFG中，利用余弦定理，可得∠EFG= 120°，故六边形EFGHIJ为正六边形，易求得该正六边形的面积为3，故正确选项为C.

评析：本题求解中关键是确定过点E与平面A1BC1平行的平面.另外部分同学可以作出该六边形，但没有经过判定就主观上认为其为正六边形.

变式3 在棱长为1的正方体ABCD-A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BC1B1内一点，若A1P∥平面AEF，则线段A1P长度的取值范围是（）.

解析：如图9所示，取B1C1的中点M，取BB1的中点N，连结A1M，A1N，MN，可以证明平面A1MN∥平面AEF，所以点P位于线段MN上，在△A1MN中，有

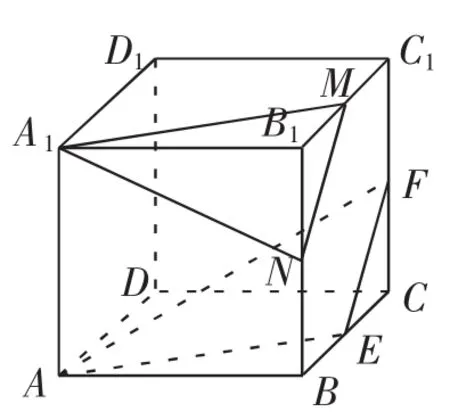
图9

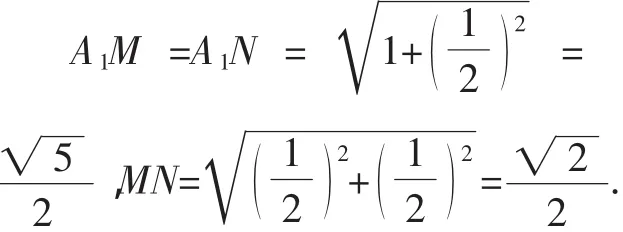
所以当点P位于M，N时，A1P最大.

当P位于MN中点O时，A1P最小，此时A1O=，所以A1O≤A1P≤A1M，即，所以线段AP长度的取值范围

1是.故选项为B.

评析：点P是面BCC1B1内的动点，但A1P∥平面AEF，故A1P应在一个与平面AEF平行的平面内，因此寻找确定的平面是本题求解的关键.

四、明确定体

例4 如图10，正方体ABCD-A1B1C1D1的棱长为1，点P，Q，R分别是棱A1A，A1B1，A1D1的中点，以△PQR为底面作正三棱柱，若此三棱柱另一底面三个顶点也都在该正方体的表面上，则这个正三棱柱的高h=____.

解析：利用三垂线定理易判断体对角线A1C与面PRQ垂直，故所求三棱柱的高所在的直线与A1C重合.

那么接下来的问题是如何确定该几何体在正方体中的位置呢？我们可以转换一下视角，既然高所以的直线与对角线重合，则该三棱柱的侧棱与体对角线平行，据此了确定该正三棱柱的位置，如图11所示，连接AC，BD相交于点M，连接PM，易判断PM平行于A1C，故PM为此三棱柱的一条棱，同理可做出其他棱（略），易知A1C=，所以PM=，故所求三棱柱的高h=

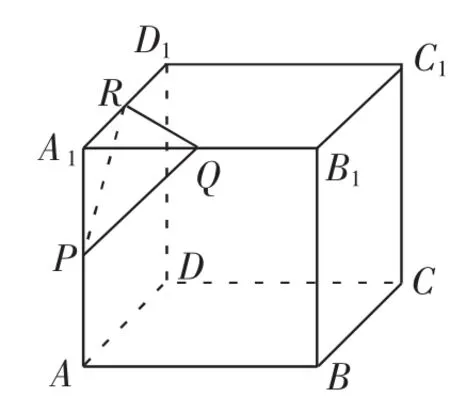
图10

图11

评析：本题只给出待求几何体的一个底面，欲求体积需要我们直观地构造出正三棱锥，那么如何构造？部分同学在解答时利用正方体的对称性，错误地认为所求三棱柱的另外一个底面在正方体的对称位置，而三棱柱的高所在的直线与体对角线重合，因此只要求出即可，再用减2倍，即可到事实是否如此呢？作出对称面后，易发现不能构成正三棱柱.因此上述解答错误.

变式4 已知A，B是球O的球面上两点，∠AOB= 90°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为（）.

A.36π B.64π C.144π D.256π

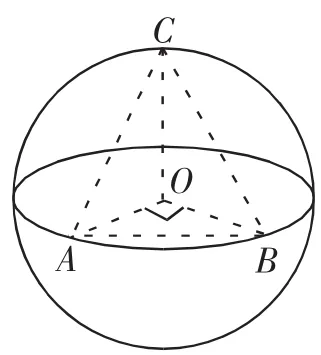
图12

解析：如图12所示，当点C位于垂直于平面AOB的直径端点时，三棱锥O-ABC的体积最大，设球O的半径为R，此时VO-ABC=VC-AOB=R2×R=，故R=6，则球O的表面积为S=4πR2=144π，故选C.

综上所述，在相关问题的求解中，只要确定关键的点、线、面、体的位置，问题即可简捷求解.同学们在解题中要善于找出关键条件的所在.