“玩转”数学，回归教育本真

☉江苏省清江中学 黄保球

“玩转”数学，回归教育本真

☉江苏省清江中学 黄保球

数学好玩吗？相信很多人持否定态度.尤其是对进入高中的不少学生而言，数学就是“噩梦”：高度抽象的概念、定理，错综复杂的关系、公式，永无休止的训练解题……，数学的确让人望而生畏.而数学家们却不赞同“数学不好玩”.“数学是艺术又是科学，她也是一种智力游戏，然而她又是描绘现实世界的一种方式和创造世界的一种力量.”（［德］E.Pi sot、M.Zamansky，著.《普通数学》）“我相信数学是人类最重要的活动之一.它不只是一种游戏，尽管我们喜欢玩它，它不只是一种艺术，尽管有时它是至高无上的艺术.”（苏格兰数学家F.F.Bonsall）“数学家导出方程或公式，就如同看到雕像、美丽的风景，听到优美的曲调等一样，从而得到充分的快乐.”（苏联数学家柯普宁）陈省身更是直言不讳的说“数学好玩”.

学生认为“数学不好玩”，于是对数学失去兴趣，而“兴趣是最好的老师”，失去“兴趣”的支撑，数学学习就难以为继；数学家认为“数学好玩”，对数学始终怀着极大的兴趣，最终取得了令人瞩目的成就.一个“玩”字道出了数学学习的真谛.但“玩”看似简单，其实意味深长，尤其是在高中数学教学中如何“玩转”数学值得探索.笔者从事数学教学十五载，面对的教学对象一直是县内的“三流”学生.这些学生由于数学基础“先天不足”，因此对于数学普遍存在“厌恶”情绪，倘若不能唤起他们对于数学的兴趣，教学效果就无从谈起.于是，笔者开始了“玩转”数学的实践与研究.

一、文学加工，玩转概念生成

数学与文学看似风马牛不相及，但实际上两者之间存在紧密联系.比如，数学抽象与文学抽象都追求某种典型性、普适性及美等；两者创作出的作品都是人类思维——逻辑的与形象的产物；文学修养是最基本的，数学修养是更高层次的修养，既有好的数学修养，也有好的文学修养，不矛盾.［1］因此，用文学视角去解读数学概念既不会失去数学的严谨，又能增加其可读性，可谓是妙趣横生，别具一番风味.

学生作品——时间函数

四季轮回，潮起潮落，阴晴圆缺，历史脚步……，这些自然、社会、生活中最正常不过的现象，它们其实都可以看成是时间的函数.时间是永恒的自变量，它可能是周期函数，日复一日，年复一年，重复着相同的变化；它可能是常数函数，同一时刻发生着相同的事情；它也可能是随机函数，飘忽不定，不可捉摸…….想必人类感受到时间威力的同时，经过理性的沉思后，产生顿悟，于是发明了函数这个概念，希望借助函数的工具破解时间留下的难题.

张奠宙先生说过：“数学有三种不同的形态，第一种是数学家创建数学结构过程中的原始状态；第二种是整理研究成果之后发表在数学杂志上、陈述于教科书上的学术形态；第三种是便于学生理解学习、在课堂上出现的教育形态.”笔者认为，数学其实还有第四种形态，那就是“学生眼中的数学”.通过文学加工，把抽象的数学概念转化为寓言故事、谜语诗歌、散文随笔等具体的文学形式，既玩出了乐趣，又展现了学生对于数学概念的个性化理解.经过玩转，数学概念变得生动形象，平易近人，从而更加易于理解，这就是玩转数学概念的最大价值所在.

二、擂台竞技，玩转复习梳理

复习就是再现学习过程，将已学知识加以梳理，纳入整体系统之中.复习课是教学诸环节中必不可少的一种课型.然而复习课并不讨学生喜欢，究其原因是复习课太枯燥乏味.复习课一般有两种偏向，一种是不进行知识技能的整理，以题海代替复习，导致学生做得苦；另一种是复习整理干巴巴，导致学生听得累.因此，要扭转目前复习课的颓势，“玩转”不失是一种很好的选择.那如何玩转复习课呢？这点我们可以从当前热播的选秀类、竞技类的电视节目中获得灵感.比如，央视的“汉字听写大会”用单纯、简朴的汉字听写手段吸引了亿万观众的参与热情，营造紧张激烈的游戏氛围，使参与者在玩转中领略汉字之美，这一点就很值得我们借鉴.

“数学英雄”车轮战

【比赛规则】把学生分成若干个学习小组，比赛前抽签确定各组的出场顺序队.比赛开始先由各组的1号队员作答，再到各组的2号队员作答：假如回答正确，教师宣布回答正确并继续出题，由下一位作答；假如回答错误，教师宣布回答错误，该名队员即被淘汰，该小组剩下的队员进行余下比赛，以此类推；最终所有队员被淘汰的队伍即判作失败，最后一支坚守在场上的队伍成为第一名.

【答题原则】凡是学生能答对的题目都让学生回答，教师不能随意打断学生的答题，教师的主要任务就是纠错和完善学生的答题过程.

【题目范例】

（1）是不是所有的对象都能构成集合，请举例说明（三个例子）.

（2）什么是空集，请举出三个关于空集的例子.

（3）A=｛x|x2+y=0｝，B=｛y|x2+y=0｝，C=｛（x，y）|x2+y=0｝，请解释上述三个集合的区别.

“擂台竞技”玩转的方式彻底扭转了传统数学复习课单调乏味的局面，学生的学习兴趣和积极性空前高涨，团队协作意识与能力得到进一步加强.在玩转过程中，数学知识得到了梳理，错误得到了纠正，思维能力得到了提升.更为重要的是实现了教师角色回归，由传统课堂的“主演”转变为现在的“导演”，从而实现了“把课堂还给学生”.

三、动手实验，玩转探究学习

在很多学生眼里数学就是解题，就是“纸上谈兵”，毫无乐趣可言.但实际上数学还可以“动手做”，可以像物理、化学那样做实验.波利亚曾指出：“数学有两个侧面，一方面它是欧几里得式的严谨科学，从这个方面看，数学像是一门系统的演绎科学，但另一方面，创造过程中的数学看起来却像是一门试验性的归纳科学.”著名的教育家弗赖登塔尔也曾指出：“要实现真正的数学教育，必须从根本上以不同的方式组织教学，否则是不可能的.在传统的课堂里，再创造方法不可能得到自由的发展.它要求有个实验室，学生可以在那儿个别活动或是小组活动.”数学实验可以分成两类，一类是借助道具和仪器的传统数学实验，另一类是借助计算机、数学软件等信息化设备的现代数学实现.数学实验需要动手操作，而动手操作必然会给学生带来无限挑战和乐趣.

传统数学实验——揭开等时曲线的奥秘

【问题提出】

在一个斜面上，摆两条轨道，一条是直线，一条是曲线，起点高度及终点高度都相同.两个质量、大小一样的小球同时从起点向下滑落，曲线的小球反而先到终点.这是由于曲线轨道上的小球先达到最高速度，所以先到达.这个现象非常符合我们的生活实际.但我们不禁要思考，存不存在这样的一条曲线轨道，小球从不同的高度同时下落时，它们同时到达最底部？

【实验过程】

步骤1：画曲线.

先用硬板纸剪一个圆盘，直径大约3.5厘米左右.取一把直尺，在直尺的边缘贴上一层双面胶，使得直尺的边缘不至于太光滑.然后把直尺搁在硬纸板上，让圆盘挨着直尺的边缘.在圆盘的边上开了一个小孔，正好可以伸进一支铅笔.当圆盘沿直尺的边缘往前滚动时，小孔里的铅笔就在硬纸板上画出了一条如图1所示的曲线.

图1

图2

步骤2：制作轨道.

把硬纸板沿着曲线剪下，剪出一块边缘为上述曲线的纸板，如图2所示.再把这张纸板沿中线垂直对折，把它一分为二.在每张纸板的底部剪开一个方形缺口，缺口大小刚好允许一个钢珠通过；沿两张硬纸板的曲线边缘分别粘上一条硬纸条，纸条的宽度比钢珠的直径稍微大一点，当然，硬纸条的外缘做的略高一些，如图3所示.这样，两条供钢珠滚动的曲线轨道做好了，如图4所示.

图3

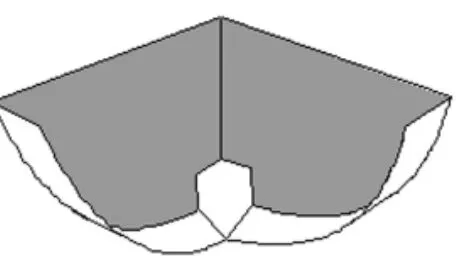
图4

步骤3：滚动实验.

两个学生一组，一个学生用手把两个曲线轨道竖直地按在桌面上固定好，另一位同学分别从两个轨道的不同高度同时释放小钢珠.反复多做几次，观察两个小钢珠向下滚动的情况，你会有什么发现.

现代数学实验——用函数图像画动物

要求：在几何画板中借助一次函数画出如图5所示的动物图形.

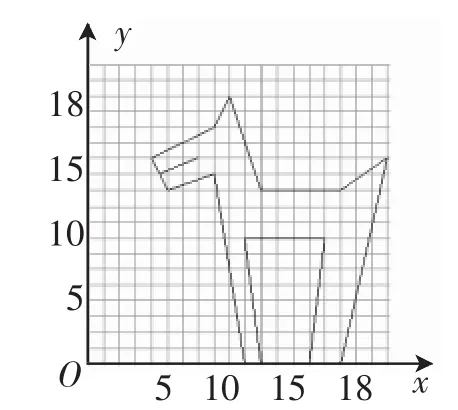
图5

新颖有趣的实验主题能够改变数学抽象枯燥的面孔，学生易于接受，可以克服注入式教学中单向传授的缺陷，构筑师生对话交流的平台，创建民主的实验环境.在实验设计的过程中，对大量的趣味性题材进行加工，力求趣味盎然贴近生活，新颖、生动有吸引力.每一个实验都是课程开发者的研究独创，融入了教师的思考和智慧，注入了活力，给学生全新的感受.

“有许多闪耀着天才光芒的思想，往往就是在玩游戏时从朦胧的想法，从有点异想天开的做法中间产生出来的”，［2］数学教育也是如此.当然，“玩转”的并不只是数学的本身，还有积极的心态.正如陈省身先生所说的“好玩就是不怎么要紧”，如果“把事情看得太严重，太有功利性，就不好玩了”，当学生觉得“数学好玩”时，便会饶有趣味地选择数学、钻研数学、热爱数学.因此，“玩转”数学不是简单的寓教于乐，而是体现了教育本真的回归.

1.黄祖达，樊启毅.漫谈数学与中国文学［J］.大学数学，2009（2）.

2.张国祥，卢兰馨.多元智能开发与评价的实验研究［M］.上海：华东师范大学出版社，2003.