基于NESSUS的兆瓦级永磁直驱风力发电机轮毂可靠性分析

周新建，李志强，涂宏斌ZHOU Xin-jian， LI Zhi-qiang， TU Hong-bin（.华东交通大学 机电工程学院，南昌 33003；.华东交通大学 轨道交通学院，南昌 33003）

基于NESSUS的兆瓦级永磁直驱风力发电机轮毂可靠性分析

周新建1，李志强1，涂宏斌2
ZHOU Xin-jian1， LI Zhi-qiang1， TU Hong-bin2
（1.华东交通大学 机电工程学院，南昌 330013；2.华东交通大学 轨道交通学院，南昌 330013）

轮毂的结构可靠性对于保障整套风力发电机系统的可靠性具有重要的作用。以1.5MW永磁直驱风力发电机的轮毂作为研究对象，利用有限元软件对其进行初步的静力分析，验证其强度安全。考虑轮毂材料力学属性的随机性以及工作载荷的随机性，将材料属性参数（弹性模量Ex、泊松比Prxy、屈服强度σS）以及各叶片叶根工作载荷参数作为随机变量引入到极限状态方程中。利用专门的可靠性分析软件NESSUS联合ANSYS的静力分析模型对轮毂结构强度进行可靠性分析，最终得到轮毂的结构可靠性指标以及各影响参数的灵敏度指标。

1.5MW永磁直驱风力发电机轮毂；静力分析；可靠性分析；灵敏度指标；NESSUS

0　引言

兆瓦级风力发电机因其体型庞大、结构复杂、工作环境严酷（如旷野、海边等），由此带来的问题就是故障率的升高。根据行业要求，对于大型联网运行的风机，可维修寿命需在20年以上，年利用率要在97%以上［1］，要实现如此高的可靠性指标，就须对风机进行可靠性和维修性设计，风机关键部件的可靠性设计就是其中重要的一部分。

轮毂作为风机的关键部件之一，它不仅需要承担来自叶片的交变载荷，还需作为变桨系统的支撑以及将转矩传递给直驱同步发电机的动轴。因此，在设计阶段将轮毂的结构可靠性纳入考虑之中对于保障整套风机的可靠性具有重要作用。现有对风力发电机轮毂的研究大多局限于对轮毂的结构强度或者疲劳强度进行分析计算［2～4］，少数涉及到对轮毂进行可靠性分析的，也仅仅是根据应力-强度干涉模型将轮毂的强度和应力简单地设置成随机正态分布，但两者分布参数（均值μ和标准差σ）都是粗糙地根据经验选取［5］，并没有深入地分析轮毂应力和强度分布的影响因素。

本文对某1.5MW永磁直驱风力发电机的轮毂进行可靠性分析，根据强度-应力干涉理论，建立了轮毂的极限状态模型，将轮毂的载荷参数以及材料的弹性模量Ex，泊松比Prxy以及屈服强度σS都作为随机变量引入到极限状态模型中，利用ANSYS联合专门的可靠性分析软件NESSUS，对风机轮毂进行了可靠性分析，定量地给出了轮毂的可靠性指标及各影响因素的灵敏度指标。其中，NESSUS作为专门的可靠性分析软件，已经被广泛地应用到诸多领域［6，7］。

1　风机轮毂功能简介及模型建立

永磁直驱风力发电机内部主要的关键性零部件有：叶片、轮毂、永磁同步发电机（定子主轴+转动轴+定子+转子+转子制动等）、机舱底座等，具体如图1所示。

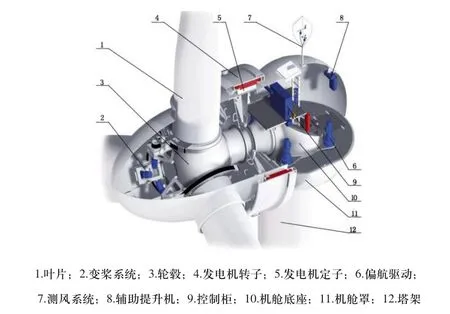
图1　直驱风力发电机内部结构示意图

其中，轮毂3联接风力发电机的三个叶片，三个叶片对称安装在轮毂上，轮毂承担来自叶片的交变载荷，同时将转矩传递给永磁同步发电机的的转轴，除此之外，轮毂上还安装有三套独立的叶片变桨系统，轮毂模型如图2所示。

图2　1.5MW永磁直驱风力发电机轮毂模型

2　基于ANSYS的轮毂有限元分析

将轮毂模型导入ANSYS软件中，考虑到轮毂所受载荷主要来自于叶片，而叶片对轮毂的受力变形具有很大的影响，因此在对轮毂进行分析时，在轮毂的三个叶片接口处分别放置一段叶片的假体。由于后续可靠性分析需要调用轮毂有限元分析的过程和结果文件，因此叶片假体的添加以及后续的网格划分、边界条件施加等都通过ANSYS的参数化语言APDL完成。

2.1轮毂有限元分析模型的建立

风力发电机轮毂和三组叶片都采用10节点四面体单元SOLID187单元划分网格，其中轮毂单元共计69910个，节点共计115278个，总体单元共计112455个，节点共计192874个，轮毂有限元模型如图3（a）所示。

2.2轮毂及叶片假体材料力学属性的赋予

轮毂及叶片的材料直接决定其屈服强度等力学属性，轮毂及叶片所选用材料的材料参数如表1所示。

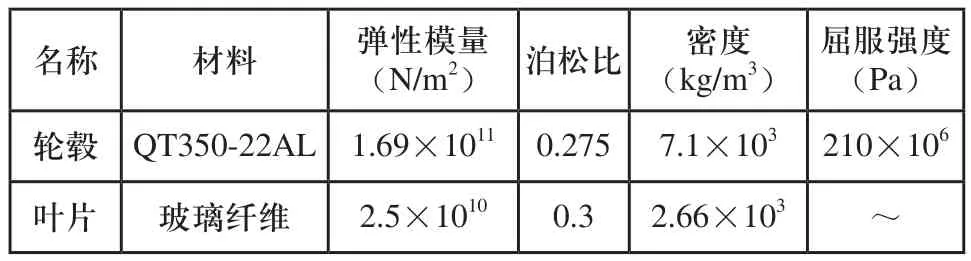
表1　轮毂及叶片的材料属性参数

2.3载荷以及边界条件的施加

风力发电机叶片以及变桨系统的重力，旋转的离心力和惯性力、风吹过叶片产生的气动载荷以及轮毂本身的重力构成了轮毂载荷。其中，叶片对轮毂的载荷都是集中在叶片和轮毂的联接位置，也就是叶根中心位置，因此在施加叶片对轮毂的载荷时，在叶片-轮毂的联接面中心建立节点，叶片对轮毂的载荷施加在其中心节点上，中心节点通过刚性梁单元MPC184与叶片假体上截面节点联接，模拟叶片传力，轮毂与主轴属于刚性联接，因此直接限制轮毂与转动主轴法兰联接面的所有自由度，同时为了约束叶片的轴向旋转，因此约束三个叶根联接面中心（即载荷加载点）的Z向的旋转，具体如图3（b）所示。

对轮毂的强度分析涉及到风机的全部工况，根据GH Bladed软件的仿真结果，可以得到叶片对轮毂的作用载荷，选取12种极限工况的载荷条件作为轮毂应力分析的基础，而载荷大小和方向都是根据叶根坐标系给出的。

2.4轮毂静力分析结果

根据轮毂的有限元分析结果，得到轮毂在各工况载荷条件下的最大等效应力情况如表2所示。

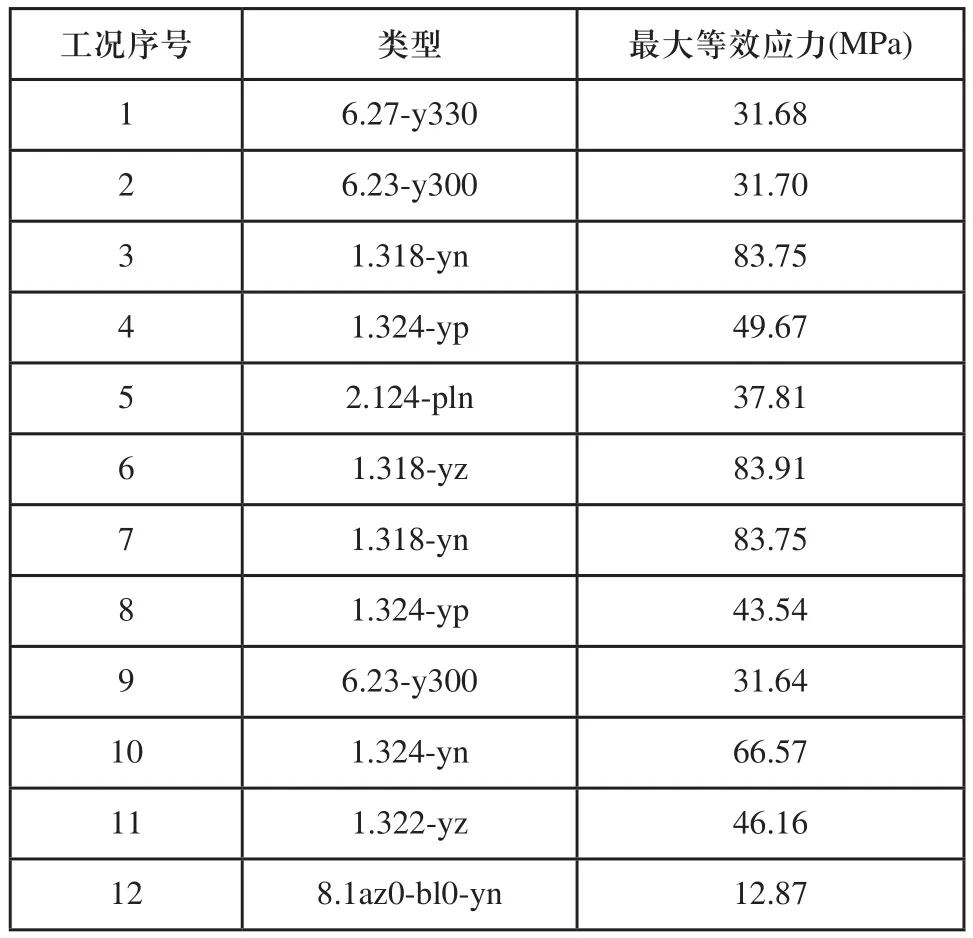
表2　各工况载荷轮毂最大等效应力数值

由此可以得到轮毂应力最大的为工况6，即1.318-yz 的83.91MPa，其中最大极限工况的具体载荷参数如表3所示，表中弯矩为kNm，力为kN，工况6载荷下轮毂的应力云图以及变形云图如图3（c）、图3（d）所示。

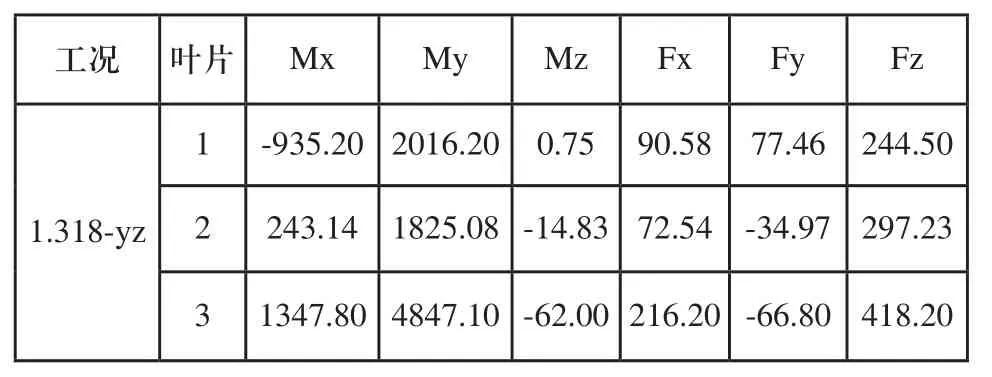
表3　最大极限工况载荷参数

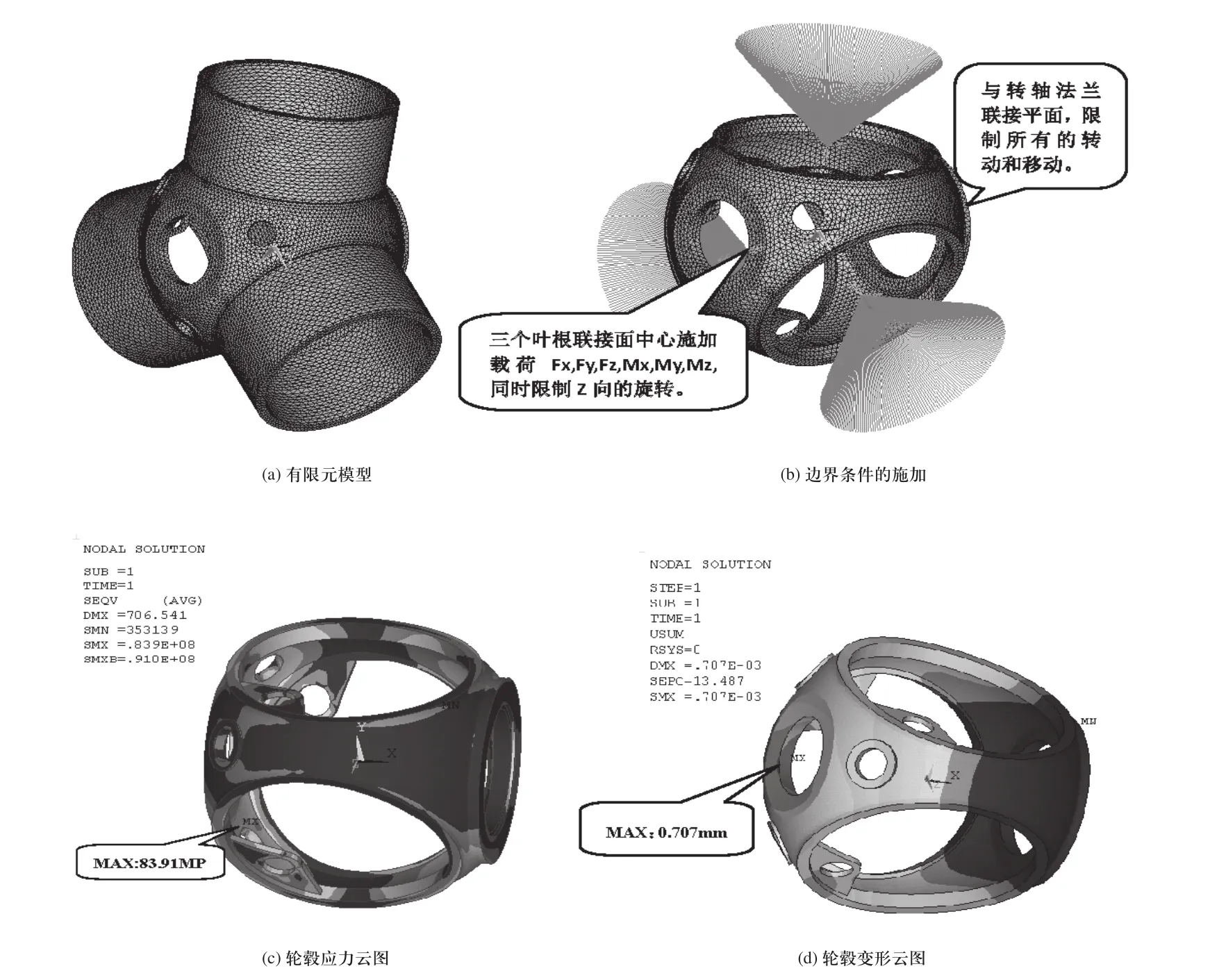
图3　轮毂有限元模型及应力分析结果

分析得到轮毂最大极限应力σmax= 83.91MPa，轮毂材料的屈服强度为σs= 200MPa，安全系数n=1.5，因此n×σmax<σs，轮毂强度符合静力学强度要求。

3　结构可靠性分析理论及分析方法

3.1 结构可靠性计算

系统可靠性都是由其部件的可靠性组成，在计算单一部件的结构可靠度时，一般是基于应力-强度干涉模型，通过分析其主要失效模式，从而建立如式（1）所示的极限状态方程。

其中，S为应力，代表能够导致部件失效的因素；R为强度，代表相应的该部件所能承受极限值；g<0为失效区域，g>0是安全区域。考虑到工作载荷、尺寸参数以及材料参数的随机性影响，方程中的应力S，强度R也都是在一定范围内变化的随机变量，两者的干涉如图4所示。

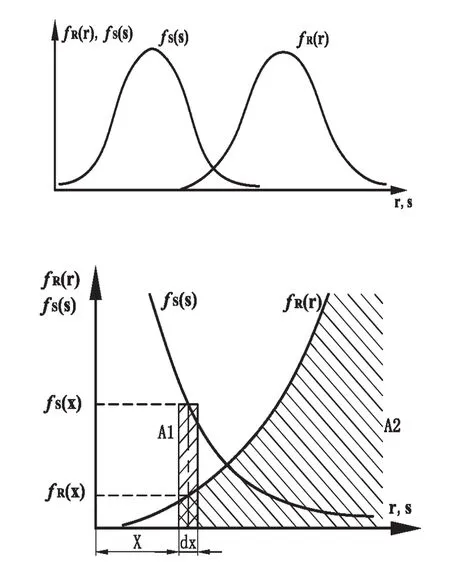
图4　应力-强度干涉模型

由应力-强度干涉模型可知，应力S在［x， x+dx］范围内的概率为A1阴影部分面积fs（x）dx。若强度R>x，则为可靠区域，其概率为A2阴影部分面积，具体如式（2）所示。如果将x变为在应力S范围内的随机变量，则强度R

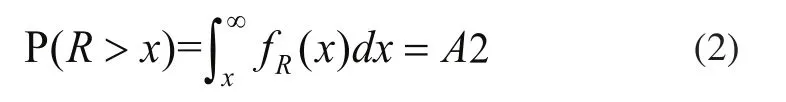
始终大于应力S的概率如式（3）所示。

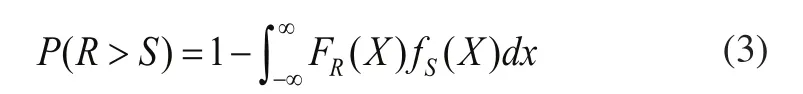
3.2基于设计验算点（MPP）的可靠性指标的定义

在实际的结构可靠性计算的过程中，零部件的极限状态方程可能由n个基本变量共同决定，如式（4）所示。

其中x1～xn一般是呈正态分布的随机变量，利用当量正态法将X转化为标准的正态分布U，则极限状态函数g（X）变换成g（U），在标准正态分布的U空间中，f（u1，u2，…，un）=0为失效面，从坐标原点到失效面f（U）=0的最短距离β，即为所求可靠性指标，部件的失效概率Pf=Φ（-β）。

图5为二维的标准化坐标系中可靠性指标定义的情况示意图，由二维推及到n维，其中P为设计验算点（MPP），其坐标为即为坐标原点到失效面的最短距离β，为设计验算点P处的单位法线向量，三者之间的关系如式（5）所示。在实际工程计算中，αi和β可以通过迭代的方式求解出来。

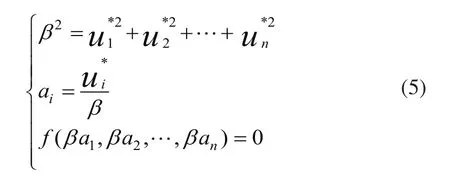
灵敏度因子为失效状态函数在设计点处的变化梯度，在确定性分析中，灵敏度的定义为在概率分析中，灵敏度定义为，表示概率随分布参数（如均值和方差）的改变而变化的程度，同时概率灵敏度分析还可以用于确定每个随机变量的重要性，而设计验算点P处的单位法线向量在U方向上来的投影，即其矢量的余弦值即可代表灵敏度，如式（6）所示。

在U空间中：

在X空间中：

这里σi表示正态分布（或者是非正态分布的近似正态）的标准方差，可见灵敏度因子为确定性灵敏度和不确定性因素（方差）的函数。

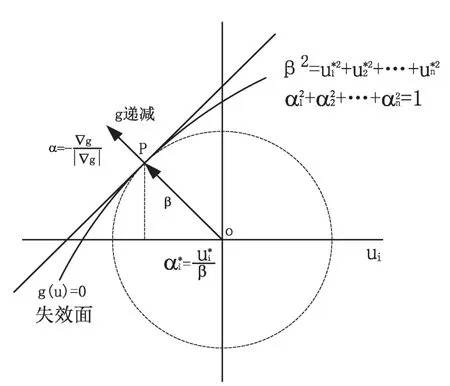
图5　二维情况下可靠性指标的定义

3.3概率分析软件NESSUS介绍

NUSSUS是美国西南研究院为NASA专门研发的一款主要用于航天飞机发动机零部件失效概率分析以及风险评估的计算机软件。后经过不断发展，现NESSUS集成了随机抽样法、解析法、组合法以及替代法等四大类，17种概率计算方法；针对随机变量，NESSUS提供17种概率密度分布函数，包括正态分布，威布尔分布，指数分布等。同时，NESSUS为用户提供了广泛的第三方接口，其可以与ANSYS、ABQUES、LS-DYNA等众多的CAE软件联合使用。NESSUS联合ANSYS进行可靠性计算的流程如图6所示。

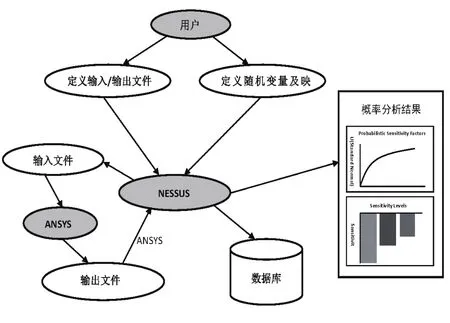
图6　NESSUS联合ANSYS工作流程

4　基于NESSUS的轮毂可靠性分析

4.1轮毂极限状态方程的建立

考虑到轮毂极限工作载荷以及材料属性参数的随机性，将轮毂的工作载荷参数以及轮毂材料属性参数（屈服强度σS、弹性模量Ex、泊松比Prxy及材料密度Density）都作为随机变量引入到极限状态方程中，根据应力-强度干涉模型建立轮毂的极限状态方程如式（9）所示。

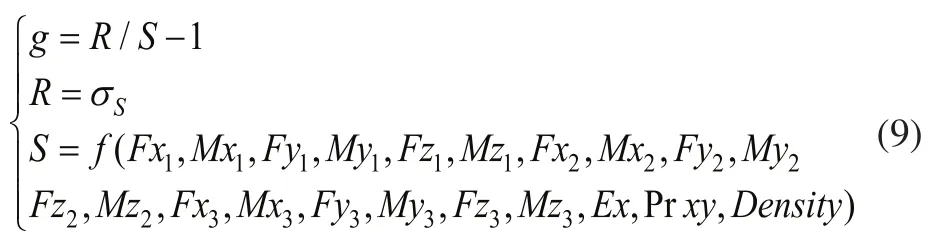
式中，f代表ANSYS有限元计算的函数；

S通过调用有限元求解的结果文件得到；

Mxi，Myi，Mzi，Fxi，Fyi，Fzi为轮毂载荷参数。

4.2各随机变量分布参数的确定

轮毂载荷参数如表3所示。根据经验，载荷参数的标准差取均值的8%，屈服强度Ex和泊松比Prxy的标准差均值的2%。屈服强度σS的标准差等于均值和轮毂材料的屈服强度变异系数的乘积，球墨铸铁的屈服强度变异系数为CS=0.04。由此可以得到轮毂各随机变量的分布参数如表4所示，其中力矩的单位为kNm，力为kN，密度为kg/m3，强度为MPa。

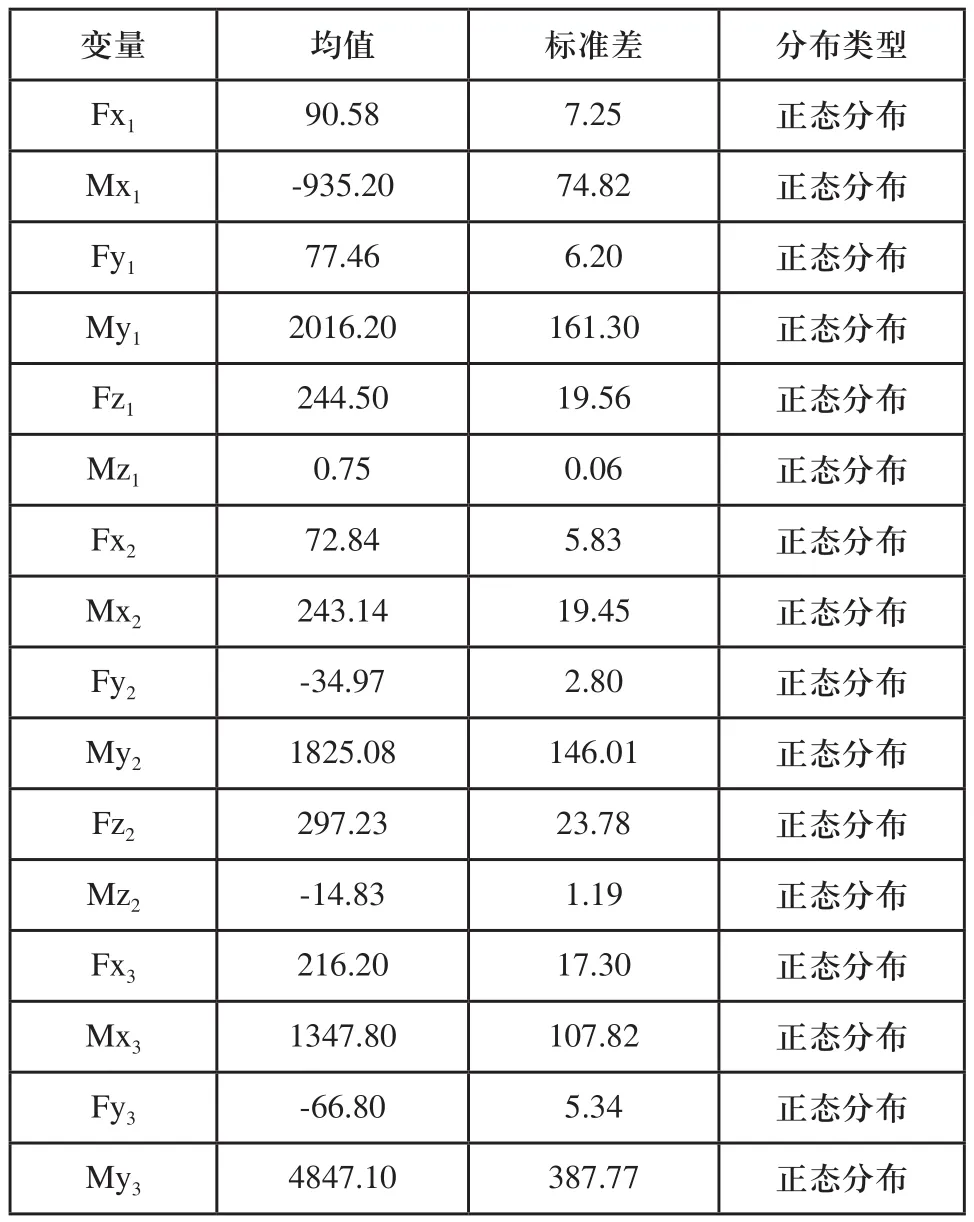
表4　各随机变量的分布参数

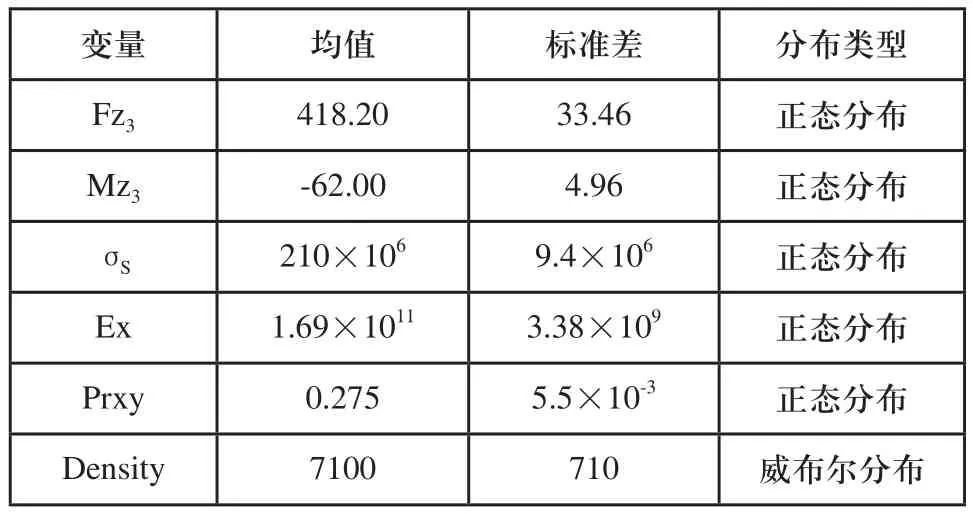
（续）

4.3概率分析方法的选择

NESSUS提供包括蒙特卡洛法（MC）、一阶矩法（FORM）、二阶矩法（SORM）、均值法（MV）及其改进方法等17种概率分析方法，在此选用一阶矩法（FORM）先进行计算，考虑到单种分析方式的计算误差，在后面采用改进均值法（AMV）以及改进均值+法（AMV+）进行验算，其中置信度设置为95%，取样误差设置为0.01。

4.4查看分析结果

利用一阶矩法（FORM），改进均值法（AMV）以及改进均值+算法（AMV+）分别求得的轮毂的可靠度结果如表5所示。运用一阶矩法（FORM）求得的轮毂的设计验算点P在X（R，Mx1，…，Prxy， Density）空间的坐标以及设计点P处的单位法线的方向参数如表6所示，表6中力矩的单位为Nm，力为N，密度kg/ m3，强度为Pa，各随机参数的灵敏度水平如图7所示。

表5　可靠性指标结果

图7　灵敏度水平结果

5　结论

轮毂的静强度分析得到最大等效应力值为83.91MPa，其与安全系数的乘积小于轮毂的屈服强度，符合轮毂的强度要求。通过NESSUS联合ANSYS对轮毂进行可靠性分析，得到该风机轮毂在极限工况下的可靠度指标为0.999996450，符合设计对轮毂可靠度的要求，对轮毂可靠性影响最大的两个随机变量分别是轮毂材料的屈服强度σS以及载荷参数My3，其余因素对轮毂的可靠度影响较小。对于屈服强度σS，灵敏度因子为=0.182，dPf/du1=-0.8449×10-12；对于载荷参数My3，灵敏度因子为=0.794，dPf/du20=0.3827× 10-10，可知屈服强度的均值增加会增加轮毂的可靠度，载荷参数My3的均值增加会降低轮毂的可靠度，这与实际情况相符。

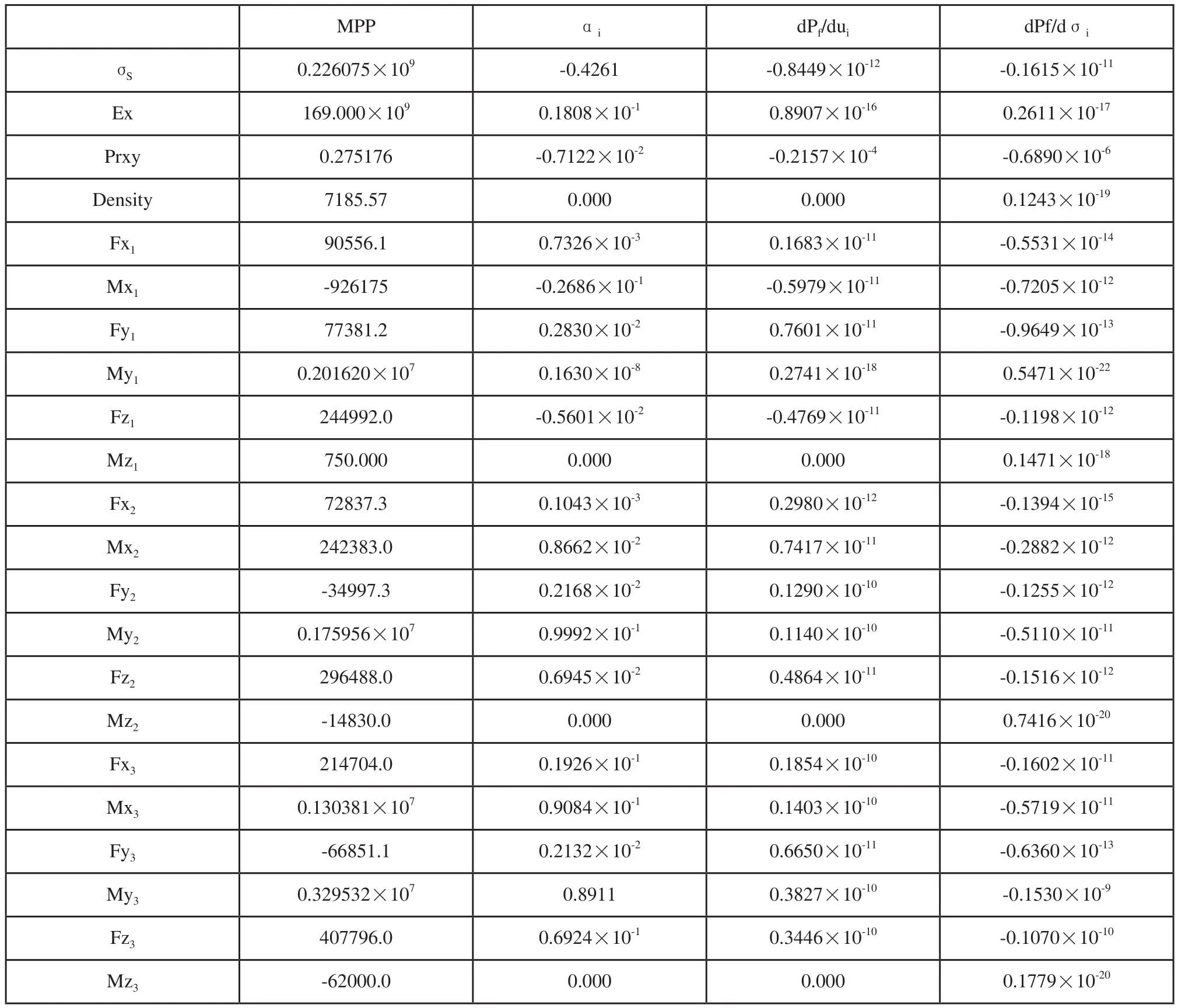
表6　灵敏度分析结果

［1］ 吴佳梁，王广良，魏振山.风力发电机可靠性工程［M］.北京：化学工业出版社，2010.

［2］ 郑甲红，杜翠.2MW风力发电机轮毂优化设计［J］.机械设计与制造，2011，（7）：7-9.

［3］ 张立刚.MW级风力发电机轮毂结构分析及优化方法的研究与应用［D］.重庆：重庆大学，2009.

［4］ 范光良，麦云飞，陈俞廷.大型风力发电机组轮毂强度分析［J］.制造业自动化，2012，34（16）：120-124.

［5］ 岳勇，谢建华，李振辉.复杂工况下风力机轮毂可靠性设计方法研究［J］.制造业自动化，2014，（2）：47-50.

［6］ 穆慧娜，张利敏，温玉全，等.基于NESSUS的空气隙传爆界面可靠性分析［J］.北京理工大学学报，2013，33（4）：331-334.

［7］ 周新建，万正平，周长国.基于NESSUS的汽车后桥可靠性灵敏度分析［J］.机械设计与制造，2009，（1）：68-70.

The reliability analysis of MW scale permanent magnet direct-drive wind generator's hub based on NEssUs

TM315

A

1009-0134（2016）08-0124-06

2016-06-22

永磁直驱风力发电机系统可靠性与维修性技术研究（20122BAB206027）

周新建（1963 -），男，教授，博士，研究方向为机械CAD/CAM和机械可靠性设计。