优化认知结构 促进数学学习

【摘 要】学生对所学知识积极主动的建构，把所学习的新知识纳入到自己的知识体系中，形成系统的知识网络，有利于加深对所学知识的理解，优化自身的认知结构，有利于及时、准确地进行知识迁移，提高解决问题的能力。

【关键词】优化；认知结构；数学学习

【中图分类号】 【文献标志码】 【文章编号】

【作者简介】章世倩，江苏省江阴市第一初级中学（江苏江阴，214431）教师，

数学老师大多有这样的体会：不少学生做数学练习时，与其说是“解题”，还不如说是“记题”。遇到曾经做过的题，可以不假思索地解答。你再问他怎么想到的，为什么这样做，他也说不清。对平时没有涉及到的新问题，就惊慌失措，信心不足。别人稍一点拨提醒，他又思如泉涌，还会发出感叹：怎么就差那么一点点。笔者认为，学生对所学知识没有形成良好的认知结构，没有形成自己的知识网络，对解决问题所需信息的提取和综合渠道不通畅，导致解决问题的视野不开阔，思维受阻。本文试图用实例谈谈如何构建和优化学生的认知结构，探究优化学生认知结构的策略。

一、重视学习规律，构建认知结构

心理学研究表明，学生对数学新知识的学习总是依赖已有的经验。这里的经验既包含已有的生活经验，也包含已有的数学知识经验和思维经历。随着所学内容的增多，学生的知识结构框架也在不断延展。学生要准确理解所学的数学概念、定理、法则，首先就要占据丰富的、符合实际的感性材料，在原有知识结构的基础上，完成对所学新知识的抽象理解。因此，我们在教学过程中，包括在布置学生课前预习时，都要有意识地引导学生寻找新知识与原有知识之间的联系，弄清它们的异同，这是知识结构框架拓展的第一个环节。如果学生能借助原有知识去发现新知识，找到新知识的生长点，这样的预习定会事半功倍。

例如，对于负数概念的引入，从形式上来看，只是在小学已学的正数前加一个“-”号，实际情况并非如此，从“正数”到“负数”是学生对数的认识上一个质的飞跃。教学中应从学生生活中大量熟悉的实例出发，如温度的“零上、零下”，货币的“收入、支出”，农作物产量的“增加、减少”等，大量具有相反意义的量，为负数的引入和理解打下初步的认知基础。

实践证明，以学生已有的经验为基础组织教学，有利于丰富学生的感性认识，加深学生对所学知识的理解，帮助学生掌握抽象概念的本质特征，同时有助于学生对抽象概念产生形象的认识，促进学生对所学知识的主动建构，初步形成结构良好的认知结构。

二、加强过程体验，优化认知结构

由于数学内容的高度抽象性，学生对所学新知识的理解不可能一步到位，学生对已有认知结构的重构和提升也会是一个循序渐进、螺旋上升的过程，所以教师要在如何加速学生认知结构的巩固提升上下功夫。

1.注重数学知识的形成过程，巩固认知结构。

例如，圆周角定理是圆中最为重要的定理之一，也蕴含了丰富的过程价值。而在实际教学中，学生对圆周角性质的认识和应用比较困难，是教学的一个难点。因此，在教学圆周角时就可以设计如下问题，通过对圆周角定理形成过程的探究，帮助学生完成对该知识的建构，强化对圆周角的认知。

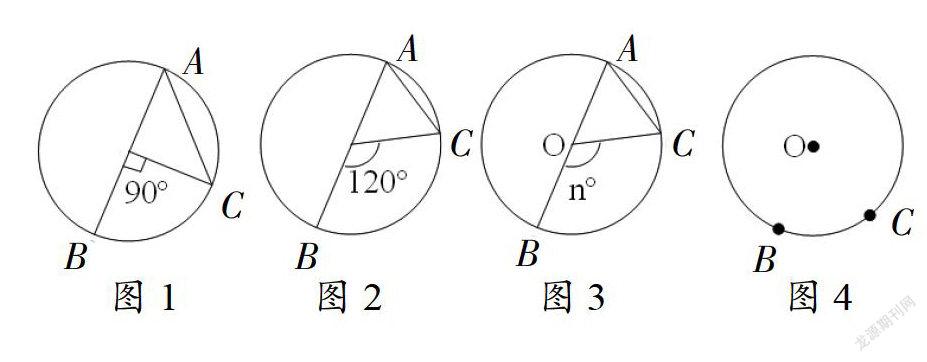
问题1：如图形所示，AB是⊙O的直径，分别求出图1、2、3中∠BAC的度数。

此问题设计的目的是通过特殊的圆周角，猜想同弧所对圆周角的度数是该弧所对圆心角度数的一半，为定理的一般情形的发现和证明提供借鉴和方法。

问题2：如图4所示， 所对的圆心角有多少个？所对的圆周角有多少个？请在图中画出 所对的圆心角和圆周角。

此问题的设计是让学生在动手操作的过程中发现，圆周角两边与圆心的三种位置关系，为定理的验证打下基础，同时也说明同弧所对的圆周角都相等。

问题3：设 所对的圆周角为∠BAC，除了圆心O在∠BAC的一边上外，圆心O和∠BAC的边还有哪些位置关系？对于这几种位置关系，前面特殊情形下猜想的∠BAC= ∠BOC还成立吗？

此问题设计层层深入，从特殊到一般来验证圆周角定理的正确性，让学生经历从操作——猜想——验证——应用的过程。

通过以上问题链的设计，学生经历了整个定理的探究过程，知道了知识的来龙去脉，对圆周角定理的知识结构的重新构建无疑是非常有益的。

2.注重知识的抽象和概括过程，提升认知品质。

数学教学中，不论定义、定理、法则、公式等知识的教学，都含有从具体到抽象和概括的过程。在抽象概括过程中认清数学对象的本质是数学学习的一般特征，从感性上升到理性，从具体到抽象，它应贯穿于数学学习与数学教学过程的始终。事实上，概念是对一类事物的属性的概括；数学技能是对一系列数学活动方式的概括；数学思想则是数学知识结构特征的概括。而只有概括了的一般概念和原理才具有较大的迁移力，故在数学教学中要注重抽象和概括的过程教学。

例如在对同类项概念进行教学时，可以提出类似“将代数式200a，5ab2，−9x2y3，100a，−13ab2，5x2y3，2a2b，−3a2b分类，并概括它们有什么共同特点”之类的问题来引入概念。对于这个问题，可以按系数正负来分，也可以按单项式的次数来分，还可以按字母和字母的指数来分。让学生经历同类项概念的探究过程，让学生概括同类项的特点，由具体上升到抽象，体现了数学教学的过程价值，提升了学生的认知品质。

三、注重网络拓展，完善认知结构

完善的认知结构不仅需要学生有良好的知识结构，还需要将所学知识连成线，织成面，编成网，实现知识结构的系统化、网络化、简约化，建立基于数学本质的、在理解基础上的广泛联系。在教学中要注意加强知识间横向和纵向的联系，帮助学生架构知识网络。

例如，在复习苏科版八年级数学下册“中心对称图形”这一部分的内容时，很多老师采用问答式的复习方法，即老师根据知识传授的顺序提出问题，学生回答；或者用做题替代对所学知识进行系统化的复习。笔者则作了如下的教学设计：

问题1：什么是平行四边形？利用平行四边形的中心对称性可得出平行四边形哪些性质？平行四边形的判定方法有哪些？

问题2：什么是矩形？矩形是如何由平行四边形特殊化得到的？矩形有哪些性质？矩形的判定方法有哪些？

问题3：什么是菱形？菱形是如何由平行四边形特殊化得到的？菱形有哪些性质？菱形的判定方法有哪些？

问题4：什么是正方形？正方形如何由菱形或矩形特殊化得到的？正方形有哪些性质？正方形的判定方法有哪些？

一组问题的设置让学生明白特殊四边形之间的逻辑关系。再通过比较相关图形的区别和联系，弄清逻辑顺序，生成学生自己的知识结构图。

数学知识蕴含着数学思想方法，数学思想方法又影响着数学知识的学习。因而，完善认知结构，不仅仅需要架构知识网络，还需要重视对数学思想方法的渗透。数学思想方法的渗透是需要教师全面深刻地认识和理解教材，深入挖掘数学知识与数学思想方法之间的关系，抓住知识形成的逻辑主线，使得教学既符合学生认知规律，也便于学生认知结构的拓展。

总之，在数学教学中，教师要充分关注学生“学”的规律，帮助学生形成结构良好的知识结构和体系，进而生成具有个性特点的认知结构。只有这样，学生才能对所学知识有更为深刻的理解和把握，才能灵活运用已有知识解决新问题。

【参考文献】

[1]吴增生.浅谈基础复习课中知识回顾与重组活动的有效开展[J].中国数学教育：初中版，2009（05）.

[2]卜以楼.意识唤醒：揭示数学本质的有效策略——以苏科版课标教材“合并同类项”教学为例[J].中学数学：初中版，2013（06）.