基于多任务委托代理的业主与承包商激励模型①

陈勇强， 傅永程， 华冬冬

(天津大学管理与经济学部， 天津 300072)



基于多任务委托代理的业主与承包商激励模型①

陈勇强， 傅永程， 华冬冬

(天津大学管理与经济学部， 天津 300072)

基于多任务委托代理并结合工程项目特点，以拓展型Cobb-Douglas生产函数反映工期、成本和质量多任务努力投入情况下工程项目的产出，构建了业主与承包商激励模型. 结果表明，承包商在工期、成本和质量任务上的最优努力水平与综合技术水平正相关，与各自任务的边际努力成本变化率负相关；业主对承包商的最优激励系数一方面受承包商自身因素影响，包括承包商的综合技术水平、绝对风险规避度以及边际努力成本变化率，另一方面取决于项目不同任务的重要性及所处环境的不确定性. 研究结果有助于业主选择适当的激励强度并实现合理的风险分担.

工程项目； 多任务； 委托代理理论； 激励模型

0　引　言

工程项目实施过程中，业主和承包商有着自身的利益诉求，存在着利益冲突[1-3]. 同时，由于双方之间的信息不对称，承包商容易产生道德风险[4]. 因此，如何激励承包商努力工作以提高项目绩效是摆在业主面前的一个重要问题[5]. 由于工程项目需要达到工期、成本和质量的多目标均衡[5-7]，本文将研究业主如何设计激励机制以实现工程项目整体绩效的优化. 围绕业主对承包商的激励问题，学者们主要在以下三个方面开展了研究：激励对项目绩效的影响，项目不同支付方式的激励机制分析，以及激励模型的建立.

激励机制的作用方面，Rose和Manley[8-9]发现合同激励条款的制定能够激发项目参与主体更加努力工作，并通过案例研究的方法识别出了影响激励机制有效性的因素. Love等[10]也发现收益共享的激励条款能够协调均衡不同利益主体的行为，并构建了针对项目成本目标的激励模型. Meng和Gallagher[5]收集了60个项目的实证数据，分析发现使用了激励机制的项目在工期、成本和质量绩效上明显高于未使用激励机制的项目.

项目的不同支付方式对应着不同的激励机制. 为克服传统总价合同、单价合同以及成本补偿合同下风险分担不均以及激励不足的问题，目标成本合同逐渐被应用在工程实践中，其支付方式可表示为F=TC+n(TC-AC). 业主和承包商事先确定目标成本TC和激励系数n，当实际成本低于目标成本时，双方根据激励系数共享成本节余；当实际成本高于目标成本时，双方共担成本超支部分. 这种支付方式均衡了业主与承包商之间的利益，有助于建立并维护双方之间良好的合作关系，实现项目成本的节约[11-12]. 然而，激励系数的确定一直是双方争论的焦点[13]，仅有少数学者通过实证研究的方法识别出了激励系数选择的影响因素[14-15]，但这些因素与激励系数的定量关系尚不明确，如何根据这些因素确定合理的激励系数仍有待解决. 此外，目标成本合同中的激励机制针对于项目的成本目标，忽视了对工期、质量目标的激励，难以实现项目工期、成本和质量的均衡优化.

激励模型的建立方面，学者们主要基于委托代理理论构建激励模型[16-19]. 然而，与传统委托代理理论研究对象相比，工程项目面临着更大的任务、自然和组织的不确定性，同时还具有多任务产出的特点，需要同时实现项目工期、成本和质量目标[20]，这些使得代理问题在工程项目中显得尤为突出[18]，需要激励承包商投入更多努力并且合理分配资源以实现项目多目标的均衡优化. 已有研究一般针对工期、成本或质量的某一目标构建单独的激励模型[21-23]，较少有文献将三者综合考虑构建整合激励模型. Hosseinian和Carmichael[18]建立了面对风险中性承包商的最优线性激励模型，并在模型中整合了针对成本和工期目标的激励. 王健等[24]在分别构造业主工期、成本和质量单属性效用函数并赋予一定权重的基础上采用线性加权的方法得到了业主的多属性效用函数，进而得到工期、成本和质量的综合均衡优化模型. 以上文献在整合项目不同任务产出时均采用线性加权的处理方式，这种简单化的处理方式虽然有助于多任务之间重要性的排序，却忽略了任务之间不可完全替代的现实，即线性模型允许某一产出的效用(如质量)为零时，业主的总效用仍不为零. 这种假定与实践中对项目绩效评价的“质量安全事故一票否决”原则并不相符. 因此，线性模型的合理性值得探讨.

要构建多任务产出情况下的激励模型，首先需要克服线性产出函数的缺陷，Cobb-Douglas生产函数由于能够反映具有不同重要性的生产要素与最终产出之间的关系在实践与研究中得到了广泛应用. 李军和刘树林[25]在考虑利润和赢得合同对供给者来说具有不同重要性的基础上，构建了基于Cobb-Douglas函数的多属性采购拍卖模型. Roels等[26]在考虑买卖双方双边道德风险问题时将双方的努力作为投入，以Cobb-Douglas生产函数反映产出，分析了不同支付类型合同的激励强弱及其对产出的影响. Sha[27]以承包商的一般性生产知识和专用知识作为投入，同样以Cobb-Douglas生产函数反映产出，求解得到合同的“弱激励区”. Cobb-Douglas生产函数的引入为本文研究多任务情况下的产出提供了很好的研究思路. 综合以上分析，本文将在遵循多任务委托代理研究逻辑的基础上构建激励模型，从而实现工程项目整体绩效的优化.

1　问题描述与模型假定

工程项目中承包商的工作任务包括三个方面：工期目标、成本目标和质量目标，用a=(a1,a2,a3)表示承包商的努力向量，其中a1是花在工期目标上的努力，a2是花在成本目标上的努力，a3是花在质量目标上的努力，ai>0 (i=1,2,3).

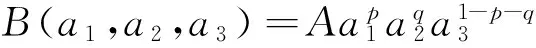
同时，由于工程项目需要同时实现工期、成本和质量目标，在某一目标上的努力投入不足将导致项目整体产出严重受损，B(a1,a2,a3)恰能反映出承包商在工期、成本或质量任一方面的投入ai趋近于零时，项目的总产出也趋于零，这在“质量安全事故一票否决”的规定下无疑是成立的. 当总产出一定时，可结合项目情况根据工期、成本和质量的相对重要性，适当调整在各方面所投入的努力以达到特定的产出，这点也可以从承包商为了赶工期而适当减少成本控制目标上的努力中得到验证.

假定3业主根据产出B(a1,a2,a3)对承包商进行激励，报酬函数取线性形式s=α+β[B(a1,a2,a3)-B0]，其中α为固定报酬，β为报酬激励系数，B0为事先约定的承包商需要达到的最低产出. 选取线性报酬函数一方面有助于提高激励机制的可操作性，业主可根据实际产出与约定的最低产出之间的差值对承包商进行奖惩，这与实践中业主在合约中规定的基于绩效的奖惩机制是相符的[11,17]；另一方面，由于一般委托代理模型中均采用线性报酬函数[16,30]，本文采用线性报酬函数有助于将分析结果与其他学者的研究结果相比较.

假定4遵循一般的委托代理分析框架，假定业主风险中性，承包商风险规避且具有不变绝对风险规避的效用函数，即u=-e-ρw，其中ρ为绝对风险规避系数，即Arrow-Pratt绝对风险规避度，w为实际货币收入.

2　模型建立

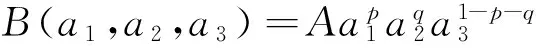
因此，承包商的确定性等价利润CE为

(1)

项目收益减去支付给承包商的报酬为

(2)

(3)

因此，在非对称信息下，业主对承包商的激励机制决策问题就是在满足承包商激励相容约束(IC)条件下选择β最大化总的确定性等价社会福利，即求解最优化问题(P)

(4)

3　模型求解

所有的ai严格为正，给定某一β值，式(4)中的激励相容约束(IC)是关于(a1,a2,a3)的极值问题，通过其一阶条件求得(IC)的驻点M(a1*,a2*,a3*)，满足

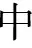
(6)

因为(IC)中的目标函数在驻点M(a1*,a2*,a3*)处连续可导，且二阶Hesse矩阵(H)如下所示

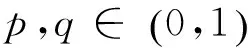
故H(M)是负定的，M(a1*,a2*,a3*)为(IC)的极大值点.

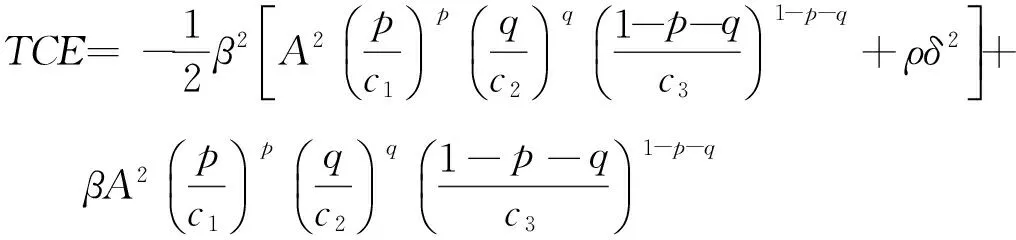
(7)

因为TCE是关于β的一元二次函数，且

ρδ2<0

所以β*即为优化问题(P)的最优激励系数.

将β*代入式(6)，得到承包商在工期、成本和质量上的最优努力水平分别为

(8)

满足

(9)

4　模型分析

4.1承包商多任务努力投入分析

命题1承包商在工期、成本和质量任务上的最优努力水平与综合技术水平正相关，与各自任务的边际努力成本变化率负相关.

证毕.

命题2承包商在工期、成本和质量任务上所投入的最优努力水平的比重由任务的相对重要性和相对边际成本变化率决定，任务越重要、相对边际努力成本变化率越低，投入的相对努力越大.

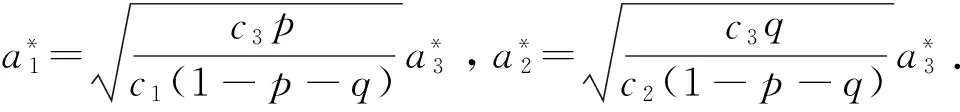
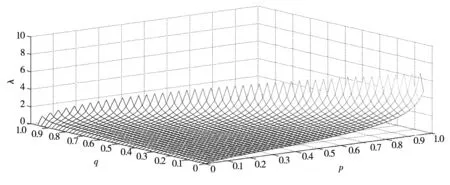
图1c1=c3时承包商相对于质量付出的最优工期努力水平

由图1可知，当p趋近于0时，λ也趋近于0，说明当工期任务的重要性较低时，承包商在工期任务上投入的努力也较低. 随着p的增加(q不变)或者q增加(p不变)时，λ的值越来越大，即随着工期任务相对于质量任务重要性的上升，承包商在工期任务上相对于质量任务所投入的努力将逐渐增加. 当p→1时，说明工期极为重要，这时λ→，承包商会将绝大部分的努力投入到工期任务上，这时可能出现为了赶工期而忽视成本和质量控制的情况，这在一些地方政府为了在考核期内迅速提升业绩而实施的项目中并不少见，由于一边倒地追求工期目标，这类项目往往容易出现成本超支严重或质量低下的问题.

同理，如图2所示，随着成本任务相对于质量任务重要性的上升，承包商在成本任务上相对于质量任务所投入的努力将逐渐增加. 当成本任务重要性极大，承包商会将绝大部分努力投入到成本任务上，这时可能出现为了尽量节约成本而忽视工期和质量控制的情况，这种情况常常反映为私人业主由于资金限制，为了节约投资而不得不适当降低工期和质量要求，承包商不得不在成本控制上将投入更多的努力.

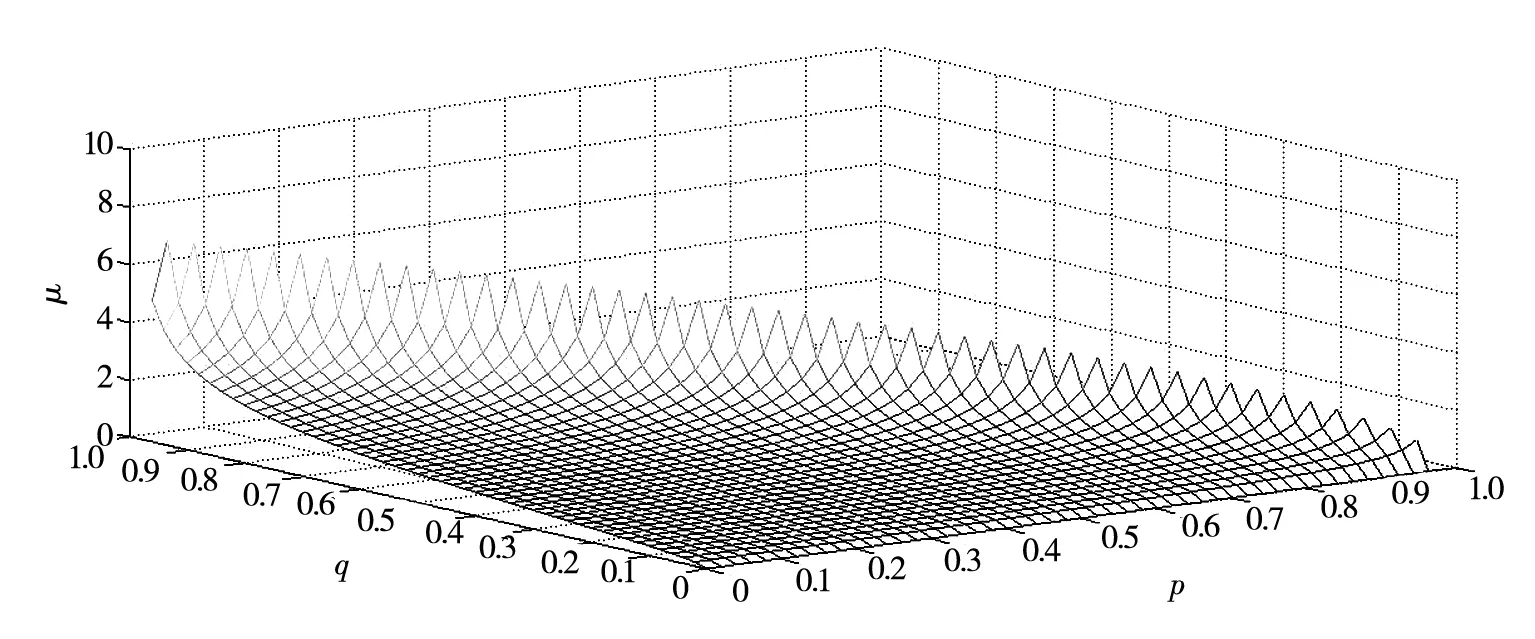
图2c2=c3时承包商相对于质量付出的最优成本努力水平

Fig. 2 The contractor’s optimal effort on cost compared to quality whenc2=c3

将图1和图2合并到一个坐标系当中，如图3所示，反映了承包商在工期、成本和质量任务上所投入努力随任务重要性的变化而变化. 在p=0附近区域内，这种情况对应于工期要求较低的项目，承包商只需在控制成本和保证一定质量上合理分配自己的努力. 在q=0附近区域内，这种情况对应于有充足资金来源的项目，在保证质量的前提下，为了满足一定的工期要求，业主对承包商的最优激励使得承包商通过投入更多的人、财、物来满足工期要求，尽管这样会使得成本增加，但资金问题并不是业主主要考虑的问题. 对于国家战略型项目而言，此类项目工期往往较为紧迫但资金充足，最优激励要求承包商将更多的努力投入到工期与质量任务上，以便在复杂多变的国际环境中抓住机遇，抢占有利时机.

图3c1=c2=c3时承包商相对于质量付出的最优工期、成本努力水平

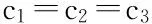
综上可知，承包商在工期、成本和质量任务上所投入努力的比重由任务的相对重要性和相对边际成本成本变化率决定，任务越重要、相对边际努力成本变化率越低，投入的相对努力越大.

证毕.

4.2最优激励系数比较静态分析

命题3最优激励系数是承包商绝对风险规避系数和外部环境不确定性的递减函数，是综合技术水平的递增函数.

所以，最优激励系数是承包商绝对风险规避系数ρ和外部环境不确定性δ2的递减函数，是综合技术水平A的递增函数.

证毕.

命题3说明，对于一定的激励强度β，ρ和δ2越大，承包商的风险成本越高，因此为了降低风险成本，最优的风险分担要求β越小. 同时，承包商的边际生产率越高，最优风险分担要求β越大.

最优激励系数是绝对风险规避系数的递减函数隐含着对于不同风险态度的承包商应采取不同的激励方案. 风险厌恶的承包商不喜欢收益水平的不确定性，如果承包商是风险厌恶的，则应减少对其产出的激励.Wang和Yuan[32]通过实证研究发现影响承包商风险态度的因素可以分为四类，即知识和经验、组织特质、个人感知以及经济环境，业主在制定激励机制时应考虑这些因素对承包商风险态度的影响. 对于从事过同类型或者在同一地区有过经验的承包商而言，由于其积累了一定的经验，能更好地预见与防范该地区该类型项目可能遇到的风险，因此有更高的风险承受能力，绝对风险规避度较低，因此对于此类承包商可以采取较强的激励. 对于资金实力较弱、组织文化偏向保守并处在不利的外部经济环境中的承包商，他们往往更偏向于风险规避，对于此类承包商应采用较弱的激励.

最优激励系数是外部环境不确定性的递减函数意味着若项目的外部环境越不确定，项目的产出难以归因为是承包商努力工作还是外界随机变量干扰所带来的，业主和承包商之间的信息不对称性增加. 项目绩效好可能是外部环境好，并不是承包商努力和能力的真实反映；反之，项目绩效不好也不一定是承包商没有努力工作，而可能是环境变动所导致的. 因此，在外部环境不确定性高的情况下，承包商的努力水平与项目的绩效相关度不高，因此提高激励强度并不能起到激励承包商努力工作的效果.

最优激励系数是综合技术水平的递增函数意味着承包商的综合技术水平越高，在相同的努力水平下能带来更大的收益，承包商越有积极性努力工作，对应的激励强度也应提高. 影响承包商风险态度的因素可能也会影响到承包商的综合技术水平，如拥有较强资金、技术实力或者有类似经验的承包商综合技术水平会更高，同时绝对风险规避度也会降低，从这两个角度出发对此类承包商都应采用较强的激励.

Badenfelt[14]通过文献浏览归纳出影响激励系数的因素包括双方感知到的风险水平、双方的风险态度，承包商对利润的追求等，并通过案例研究的方法识别出另外三个影响因素，包括双方对公平的感知、专业知识以及双方长期关系，命题3所揭示的关系则从定量化的角度支持了上述研究结论.

命题4在其他条件相同的情况下，在极值点处，较高的工期、成本和质量目标的边际努力成本变化率之和导致较低的最优激励强度，反之亦然.

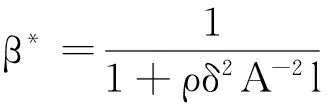
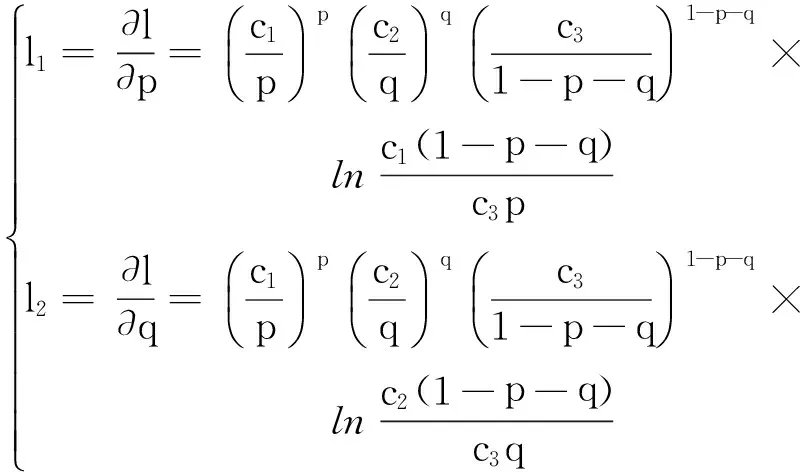
证毕.

命题4表明，在极值点处，若工程项目的边际努力成本变化率之和越大，应采取较低的激励强度. 如果边际成本变化率之和越大，则承包商额外的努力伴随着努力成本的大幅上升，根据命题4，此时应采取较弱的激励.

命题5给定ρ和δ2，当工期、成本和质量目标上的相对重要性与其边际努力成本变化率所占边际努力成本变化率之和的比重相接近时，最优的激励强度较弱.

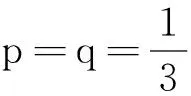
证毕.

图4l的曲面

Fig. 4Thecurvedsurfaceofl

命题5表明，当项目中某项任务的相对重要性及承包商完成此项任务付出一定努力所需花费的代价不相匹配，远离“弱激励区”时，即存在某项任务相对重要性高且承包商完成此项任务付出的努力成本较低时，业主所选择的最优激励系数会较高，此时较强的激励会鼓励承包商付出更多的努力以较小的代价去完成重要性较高的任务，从而带来更高的项目产出，这对于业主和承包商来说是一个双赢的局面.

综合命题3、命题4和命题5可知，业主对承包商的最优激励系数取决于两方面因素，其一是承包商自身因素，包括承包商的综合技术水平、绝对风险规避度和边际努力成本变化率；另一方面是项目及环境因素，包括项目不同任务的重要性及所处环境的不确定程度. 工程实践中，最优激励系数的确定不能只依据于承包商或项目其中一方的特点，需要综合考虑二者在相关参数上的关联性，从而选择既满足项目特点又针对特定承包商的最优激励系数.

5　结束语

本文基于多任务委托代理构建了工程业主与承包商激励模型，并结合工程项目特点，以拓展型Cobb-Douglas生产函数反映工期、成本和质量多任务努力投入情况下工程项目的产出. 研究结果表明，承包商在工期、成本和质量任务上的努力水平与综合技术水平正相关，与各自任务的边际努力成本变化率负相关；同时，在三个任务上投入的相对努力水平由任务的相对重要性和相对边际成本变化率决定，任务越重要、相对边际努力成本变化率越低，投入的相对努力越大. 研究结果有助于承包商为达到一定的总产出而合理分配自身资源，付出相应的努力水平.

此外，业主对承包商的最优激励系数受两方面因素的影响，一方面是承包商自身因素，包括承包商的综合技术水平、绝对风险规避度以及边际努力成本变化率，对于综合技术水平更高的承包商可采用较强的激励，而面对风险规避度更高的承包商则应采用较弱的激励，较大的边际成本变化率之和导致在极值点处取得的最优激励系数变得更低；另一方面是项目及环境因素，主要指项目不同任务的重要性及所处环境的不确定性，项目越复杂、所处环境不确定性越高，则越难判断承包商在工作中所付出的实际努力水平，因而该采用较弱的激励.

对于工程实践者而言，选择适当的激励强度并在业主与承包商之间进行合理的风险分担是项目成功的一个重要保证，在本文识别的最优激励系数的影响因素基础上，业主可根据项目、所处环境及承包商的特点选择合理的激励强度，从而激励承包商努力工作，实现双方共赢.

需要注意的是，工程项目的不同阶段工期、成本和质量任务的重要性是不同的，具有动态变化性，如项目建设后期工期控制变为首要目标，质量控制则随着时间推移而逐渐增强，因此未来研究可在本文所构建的静态模型的基础上考虑工程项目多任务之间重要性的动态变化性以进一步深化激励模型. 同时，本文为了模型的简洁性在承包商的努力成本假定上做了一定的妥协，假定多任务努力成本之间相互独立，然而更贴近实际的情况是，承包商在工期、成本和质量上的投入具有一定的替代性，如在工期上投入更多的努力，会使得质量上的边际努力成本上升，工期与成本、成本与质量之间也存在这种任务替代性. 因此，识别承包商在每项任务上的努力对努力成本的影响，并在任务之间相互替代的基础上构造承包商努力成本函数是未来研究需要解决的另一个问题.

[1]Zhang L, He J, Zhou S. Sharing tacit knowledge for integrated project team flexibility: Case study of integrated project delivery[J]. Journal of Construction Engineering and Management, 2013, 139(7): 795-804.

[2]谭志加, 杨海, 陈琼. 收费公路项目Pareto有效BOT合同与政府补贴[J]. 管理科学学报, 2013, 16(3): 10-20.

Tan Zhijia, Yang Hai, Chen Qiong. Pareto-efficient BOT contracts for road franchising with government subsidy[J]. Journal of Management Sciences in China, 2013, 16(3): 10-20. (in Chinese)

[3]高颖, 张水波, 冯卓. 不完全合约下PPP项目的运营期延长决策机制[J]. 管理科学学报, 2014, 17(2): 48-57, 94.

Gao Ying, Zhang Shuibo, Feng Zhuo. Analysis of decision-making mechanism for operation period extension of public-private partnership projects under incomplete contracts[J]. Journal of Management Sciences in China, 2014, 17(2): 48-57, 94. (in Chinese)

[4]Schieg M. Strategies for avoiding asymmetric information in construction project management[J]. Journal of Business Economics and Management, 2008, 9(1): 47-51.

[5]Meng X, Gallagher B. The impact of incentive mechanisms on project performance[J]. International Journal of Project Management, 2012, 30(3): 352-362.

[6]Ozcan-Deniz G, Zhu Y, Ceron V. Time, cost, and environmental impact analysis on construction operation optimization using genetic algorithms[J]. Journal of Management in Engineering, 2012, 28(3): 265-272.

[7]Mungle S, Benyoucef L, Son Y J, et al. A fuzzy clustering-based genetic algorithm approach for time-cost-quality trade-off problems: A case study of highway construction project[J]. Engineering Applications of Artificial Intelligence, 2013, 26(8): 1953-1966.

[8]Rose T M, Manley K. Client recommendations for financial incentives on construction projects[J]. Engineering, Construction and Architectural Management, 2010, 17(3): 252-267.

[9]Rose T M, Manley K. Financial incentives and advanced construction procurement systems[J]. Project Management Journal, 2010, 41(1): 40-50.

[10]Love P E, Davis P R, Chevis R, et al. Risk/reward compensation model for civil engineering infrastructure alliance projects[J]. Journal of Construction Engineering and Management, 2011, 137(2): 127-136.

[11]Chan D W M, Chan A P C, Lam P T I L, et al. An empirical survey of the motives and benefits of adopting guaranteed maximum price and target cost contracts in construction[J]. International Journal of Project Management, 2011, 29(5): 577-590.

[12]Zimina D, Ballard G, Pasquire C. Target value design: Using collaboration and a lean approach to reduce construction cost[J]. Construction Management and Economics, 2012, 30(5): 383-398.

[13]Boukendour S, Hughes W. Collaborative incentive contracts: Stimulating competitive behaviour without competition[J]. Construction Management and Economics, 2014, DOI: 10.1080/01446193.2013.875215.

[14]Badenfelt U. The selection of sharing ratios in target cost contracts[J]. Engineering, Construction and Architectural Management, 2008, 15(1): 54-65.

[15]Chan J H L, Chan D W M, Lam P T I L, et al. Preferred risk allocation in target cost contracts in construction[J]. Facilities, 2011, 29(13/14): 542-562.

[16]袁江天, 张维. 多任务委托代理模型下国企经理激励问题研究[J]. 管理科学学报, 2006, 9(3): 45-53.

Yuan Jiangtian, Zhang Wei. Multitask principal-agent model and study on SOE managers’ incentive issues[J]. Journal of Management Sciences in China, 2006, 9(3): 45-53. (in Chinese)

[17]Hosseinian S M, Carmichael D G. Optimal gainshare/painshare in alliance projects[J]. Journal of the Operational Research Society, 2013, 64(8): 1269-1278.

[18]Hosseinian S M, Carmichael D G. Optimal incentive contract with risk-neutral contractor[J]. Journal of Construction Engineering and Management, 2013, 139(8): 899-909.

[19]张宗明, 廖貅武, 刘树林. 需求不确定性下IT服务外包合同设计与分析[J]. 管理科学学报, 2013, 16(2): 46-59.

Zhang Zongming, Liao Xiuwu, Liu Shulin. Design and analysis of contracts for IT service outsourcing with uncertain requirements[J]. Journal of Management Sciences in China, 2013, 16(2): 46-59. (in Chinese)

[20]Yang L R, Chen J H, Huang C F. A comprehensive framework for evaluating key project requirements[J]. Journal of Civil Engineering and Management, 2013, 19(sup1): S91-S105.

[21]Bubshait A A. Incentive/disincentive contracts and its effects on industrial projects[J]. International Journal of Project Management, 2003, 21(1): 63-70.

[22]Motawa I, Kaka A. Modelling payment mechanisms for supply chain in construction[J]. Engineering, Construction and Architectural Management, 2009, 16(4): 325-336.

[23]何正文, 刘人境, 胡信布. 基于合同双方交互作用的项目调度优化[J]. 管理科学学报, 2014, 17(8): 48-59.

He Zhengwen, Liu Renjing, Hu Xinbu. Project scheduling optimization based on interaction between two parties of contracts[J]. Journal of Management Sciences in China, 2014, 17(8): 48-59. (in Chinese)

[24]王健， 刘尔烈， 骆刚. 工程项目工期―成本―质量综合均衡优化[J]. 系统工程学报, 2004, 19(2): 148-153.

Wang Jian, Liu Erlie, Luo Gang. Analysis of time-cost-quality tradeoff optimization in construction project management[J]. Journal of Systems Engineering, 2004, 19(2): 148-153. (in Chinese)

[25]李军, 刘树林. 基于Cobb-Douglas效用函数的多属性采购拍卖[J]. 管理科学学报, 2012, 15(3): 54-60.

Li Jun, Liu Shulin. Multi-attribute procurement auctions based on Cobb-Douglas utility function[J]. Journal of Management Sciences in China, 2012, 15(3): 54-60. (in Chinese)

[26]Roels G, Karmarkar U S, Carr S. Contracting for collaborative services[J]. Management Science, 2010, 56(5): 849-863.

[27]Sha K. Vertical governance of construction projects: An information cost perspective[J]. Construction Management and Economics, 2011, 29(11): 1137-1147.

[28]温新刚, 刘新民, 丁黎黎, 等. 动态多任务双边道德风险契约研究[J]. 运筹与管理, 2012, 21(3): 212-219.

Wen Xingang, Liu Xinmin, Ding Lili, et al. Study on multi-task dynamic incentive contract design based on double moral hazard prevention[J]. Operation Research and Management Science, 2012, 21(3): 212-219. (in Chinese)

[29]倪得兵, 戴春爱, 唐小我. 外生的隐性“关系”与显性激励[J]. 管理工程学报, 2011, 25(3): 139-147.

Ni Debing, Dai Chunai, Tang Xiaowo. Implicit “guanxi” and explicit incentive[J]. Journal of Industrial Engineering/Engineering Management, 2011, 25(3): 139-147. (in Chinese)

[30]何山, 徐光伟, 陈泽明. 代理人自利行为下的最优激励契约[J]. 管理工程学报, 2013, 27(3): 139-144, 155.

He Shan, Xu Guangwei, Chen Zeming. Optimal incentive contracts under agents’ self-interested behavior[J]. Journal of Industrial Engineering/Engineering Management, 2013, 27(3): 139-144, 155. (in Chinese)

[31]Laffont J, Martimort D. The Theory of Incentives: The Principal-Agent Model[M]. New Jersey: Princeton University Press, 2002: 230-232.

[32]Wang J, Yuan H. Factors affecting contractors’ risk attitudes in construction projects: Case study from China[J]. International Journal of Project Management, 2011, 29(2): 209-219.

A multi-task incentive model between the owner and contractor

CHENYong-qiang,FUYong-cheng,HUADong-dong

College of Management and Economics, Tianjin University, Tianjin 300072, China

Considering the characteristics of construction projects, a multi-task incentive model between the owner and contractor was established based on the principal-agent theory. An extended form of Cobb-Douglas production function was built to reflect the outcome of construction projects in the circumstances of multi-dimensional efforts invested in schedule, cost and quality. Results indicate that the optimal amount of effort devoted to each of the three tasks is positively associated with the total factor productivity, and negatively associated with the marginal changing rate of cost-of-effort. Besides, the optimal incentive coefficient is influenced by two kinds of factors: one is related to the contractor, including the total factor productivity, absolute risk-aversion coefficient, and the marginal changing rate of cost-of-effort; the other is related to the significance of each task and the uncertainty of the circumstances. Our research results could help the owner select appropriate incentive intensity and achieve reasonable risk sharings.

construction project; multi-task; principal-agent theory; incentive model

① 2014-03-19；

2014-11-20.

国家自然科学基金资助项目(71231006; 71072156).

陈勇强(1964—)， 男， 河北冀县人， 博士， 教授， 博士生导师. Email: symbolpmc@vip.sina.com

F284

A

1007-9807(2016)04-0045-11