基于DEA/AR博弈交叉效率方法的学术期刊评价研究①

李　琳， 黄海军， 汪寿阳

(1. 北京航空航天大学经济管理学院， 北京 100191； 2. 中国科学院数学与系统科学研究院， 北京 100190)



基于DEA/AR博弈交叉效率方法的学术期刊评价研究①

李琳1, 2， 黄海军1， 汪寿阳2

(1. 北京航空航天大学经济管理学院， 北京 100191； 2. 中国科学院数学与系统科学研究院， 北京 100190)

学术期刊的评价问题是期刊研究领域的重要课题之一. 传统数据包络分析方法在评价多维指标下的期刊绩效时都是基于“自评”模式. 由于未能考虑“他评”，造成评价结果容易被夸大等问题. 本文在非合作博弈框架下基于数据包络分析/保证域博弈交叉效率方法研究期刊的投入产出绩效评价问题，并选取17种中国科技核心期刊为例展开分析. 研究发现：1) 某些具有很高行业影响力的期刊，虽然具有较高的产出值，但是刊文量较多，导致实际评价结果不够理想；2) 指标权重的偏好变化会使得期刊评价值出现增加、不变和减少三种情况；3) 期刊在自引频次上存在着过度、适度和不足三种情形. 相关评价结果可为期刊工作者在提升期刊竞争力方面提供决策参考.

期刊评价； 数据包络分析； 效率评价； 非合作博弈； 保证域

0　引　言

当前我国共有9 800多种期刊，其中科技期刊有4 953种. 从期刊工作者的角度来看，由于同种类型的期刊之间通常会存在着不同程度的竞争关系，因此期刊工作者通常会较为关注同行期刊的办刊质量和竞争力排名变化，这将会为期刊未来的工作导向提供决策支持. 从学术水平对比的角度来看，大到一个国家，小到一所学校一个科研单位，其学术水平高低的横向对比常通过期刊论文的数量和质量得到体现. 因而，学术期刊的评价问题一直是期刊领域重要的研究课题之一，已引起相关学者的持续关注.

自文献计量学被Garfield[1]开创以来，已有大量的文献计量指标被提出，如总被引频次、影响因子、被引半衰期、来源文献量和引用期刊数等. 由于这些单一指标都是从一种参考视角出发，仅用一种指标进行期刊评价得到的评价结果将是片面的[2]. 因此，采用多维指标对期刊展开评价的多属性评价方法在学术期刊评价领域得到了越来越广泛的应用[3]，其中的代表性方法之一是数据包络分析(data envelopment analysis，DEA)方法[4].

DEA模型首次由运筹学家Charnes，Cooper和Rhodes于1978年正式提出，简称CCR DEA模型[4]. DEA作为一种著名的非参数数学规划方法，被广泛应用于评价具有多维评价指标结构的同质决策单元(decision making unit，DMU)相对效率. 由于在DEA方法下，多维评价指标的最优权重是根据观察到的数据计算得到，避免了因主观赋予多维指标权重而给评价结果带来不确定性的缺点，同时它还具有不需要假定生产函数等优点，因此自CCR DEA模型被正式提出以来，已有BCC DEA模型、超效率DEA模型、加性DEA模型等多种DEA模型被提出[5]，并在环境[6]、产业政策[7]、银行[8]等多种领域得到了广泛的应用.

本文在非合作博弈框架下基于交叉效率DEA方法[9-10]研究期刊的投入产出绩效评价问题，以避免传统DEA模型由于从“自评”视角出发而带来的容易产生夸大自身长处、回避自身缺陷、产生表面DEA有效等问题[11]. 具体来说，考虑到同类期刊之间的竞争关系，本文将非合作博弈理论引入到DEA交叉效率方法中，利用Liang等[12]提出的博弈DEA交叉效率方法对学术期刊开展评价工作，以便于评价结果能够容易被期刊工作者和相关学者接受. 此外，考虑到在期刊的评价实践中，期刊工作者对不同评价指标的重要性可能会存在着偏好认识. 为了保证评价结果更加符合实际，保证域(assurance region，AR)[13]也被考虑到博弈DEA交叉效率方法之中，通过构建的DEA/AR(data envelopment analysis /assurance region)评价期刊的投入产出绩效.

1　文献回顾

学术期刊的评价研究可以追溯到Garfield[1]系统地提出文献计量学. 早期的学术期刊评价方法采用的是单一文献计量指标，如总被引频次、影响因子、被引半衰期、来源文献量和引用期刊数等. 随着学术期刊评价研究的深入，包含更多信息量的复合评价指标被不断提出，如相对引用指标RI[14]、标准平均引用率NMCR[15]、学科论文平均被引用次数[16]、H指数[17]、特征因子Eigenfactor[18]、论文计数影响因子ACIF[19]等. 这里任一评价指标都是从某个特定视角去对学术期刊展开评价，具有计算直观简单、容易解释等优点，但是容易导致对同样一本期刊，从不同角度出发的评价结果可能会相差较大，无法给出统一的评价结果. 因此用单一指标评价学术期刊是片面的[2].

为了得到更加全面的期刊评价结果，针对多维指标的各种多属性评价方法得到了重视并被不断地引入到学术期刊评价领域的研究中，如DEA模型[20]、层次分析法[21]、结构方程模型[22-23]、灰色关联法[24]、主成分分析法[25]等. 在实践中，目前中国科技信息研究所开展的中国科技期刊综合评价指标体系研究得到了我国期刊界的认可. 该研究采用层次分析法，由专家打分确定重要指标的权重，并分学科对每种期刊进行综合评定. 综合评估法的目的是消除单一指标评估带来的局限性，从影响期刊发挥其作用的各个方面对期刊进行评价. 但是专家打分步骤易受专家个人因素影响而导致结果产生波动.

相关学者已经注意到这些多属性评价方法都或多或少地存在着自身的不足，如王小唯等[20]基于DEA方法展开期刊评价研究时，是基于传统的自评模式得到评价结果，未能将他评结果反映到最终的评价结果中，容易造成夸大自身效率等问题；层次分析法中专家评估过程受专家的知识水平、知识结构和偏好等因素影响较大等. 为了克服这些不足，相关研究主要从以下两个方向深入展开[3]：一种是不同评价方法进行组合及应用，另一种是对特定评价方法深入的优化与创新. 本文属于第二种研究方向，充分考虑了学术期刊之间在绩效评价过程中的博弈关系，将自评与他评充分相结合，在非合作博弈框架下展开博弈，且最终得到一组评价结果是纳什均衡解.

2　DEA/AR博弈交叉效率方法

2.1DEA博弈交叉效率方法

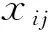
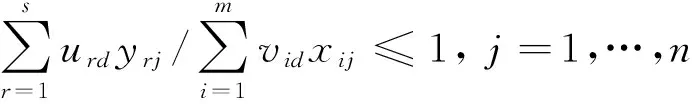
urd,vid≥0,i=1,…,m;r=1,…,s

(1)

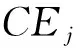
(2)

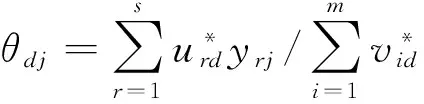
DEA博弈交叉效率方法是基于非合作博弈框架展开的研究. 它的大致思路是：当期刊d的评价值为αd时，则其他期刊以不损害期刊d的评价值(不降低αd)为前提，计算各自的最大评价值，记为αdj. 其计算表达式为

(3)

对于期刊j，可以通过下列模型得到其评价值αdj(d∈{1,…,n}，j=1,…,n)

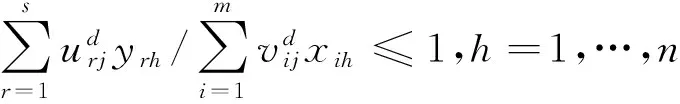
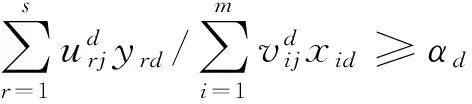
(4)

模型(4)通过C-C变换[26]，可以转换为下列等价的模型

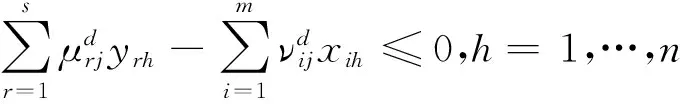
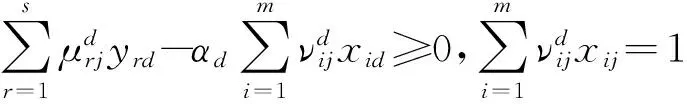
(5)

对于每个d∈{1,…,n}，DMUj(j=1,…,n)基于模型(5)各计算一次，则得到下列矩阵的各行. 由于d可以取n次，因此，可以得到下面的矩阵

(6)

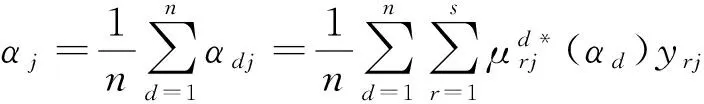
DEA博弈交叉效率算法如下[12]：

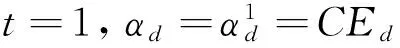
Liang等[12]已经证明了博弈DEA算法的收敛性，且其所得到的解是纳什均衡解. 此外，算法步骤1中任意的初始效率值αd都会得到唯一的博弈交叉效率值.

2.2存在保证域的DEA博弈交叉效率方法

在科技期刊的评价过程中，评价者对各评价指标的重要性可能会有自己的偏好认识. 因此需要根据实际情况，将相关权重偏好信息引入到DEA博弈交叉效率模型之中，构建存在保证域的DEA博弈交叉效率方法，以使得期刊评价结果更加容易被接受.

通常地，保证域有两种常见的形式，即“绝对范围”(absolute range)和“相对范围”(relative range). 他们的数学表达式分别如式(7)和式(8)所示

(7)

(8)

本文选取“相对范围”作为保证域. 这是由于DEA方法的结果与投入或产出数据的量纲无关，即投入或产出数据按某种比例变化时，DEA模型的最优值能够保持不变. “相对范围”可以满足DEA方法的这种单位不变性性质，且他无需像“绝对范围”那样考虑权重具体的范围，仅需要估计权重之间的重要性程度大小即可，这也有效地降低了操作的难度.

因此，将式(8)纳入到模型(5)之中，即可构成存在保证域的DEA模型. DEA博弈交叉效率算法步骤2中的模型(5)换成这种新构建的DEA/AR模型，即可得到DEA/AR博弈交叉效率算法.

定理1博弈DEA/AR算法是收敛的，且所得到的最优解是纳什均衡解.

3　实证应用

由于DEA方法是基于已经观察到的数据评价DMU的相对效率，因此选取何种评价指标会直接影响到评价结果. 另外，对于一定数量的样本，评价指标选取过多会降低DEA的判别能力[27-28]. 因此，需要根据评价目的选取关键性的评价指标并注意适度控制评价指标的数量. 通常地，指标数量尽量控制在样本数量的三分之一内[29].

根据这一思路，为了较为综合地衡量各期刊在行业中的相对地位，考虑到期刊的实际运作特点，本文选取期刊评价工作中常用的“来源文献量”(X)作为投入指标，“基金论文”(Y1)、“引用刊数”(Y2)、“被引半衰期”(Y3)、“他引频次”(Y4)或“总被引频次”(Y5)、和“影响因子”(Y6)作为产出指标. 将“他引频次”和“总被引频次”分别考虑的原因是通过对评价结果的比较，便于发现自引频次对各期刊的影响. 因此，本文构建的指标评价体系有两套，分别是(X,Y1,Y2,Y3,Y4,Y6)和(X,Y1,Y2,Y3,Y5,Y6)，选取的指标数量控制在样本数量的三分之一左右，对DEA的判别能力影响不大.

3.2指标数据搜集

本文从国家自然科学基金委管理科学部认定的30种管理科学重要学术期刊中，选取17种中国科技核心期刊作为样本展开分析. 根据上节所选取的评价指标，从《2014年版中国科技期刊引证报告(核心版)》中搜集相关数据(见表1).

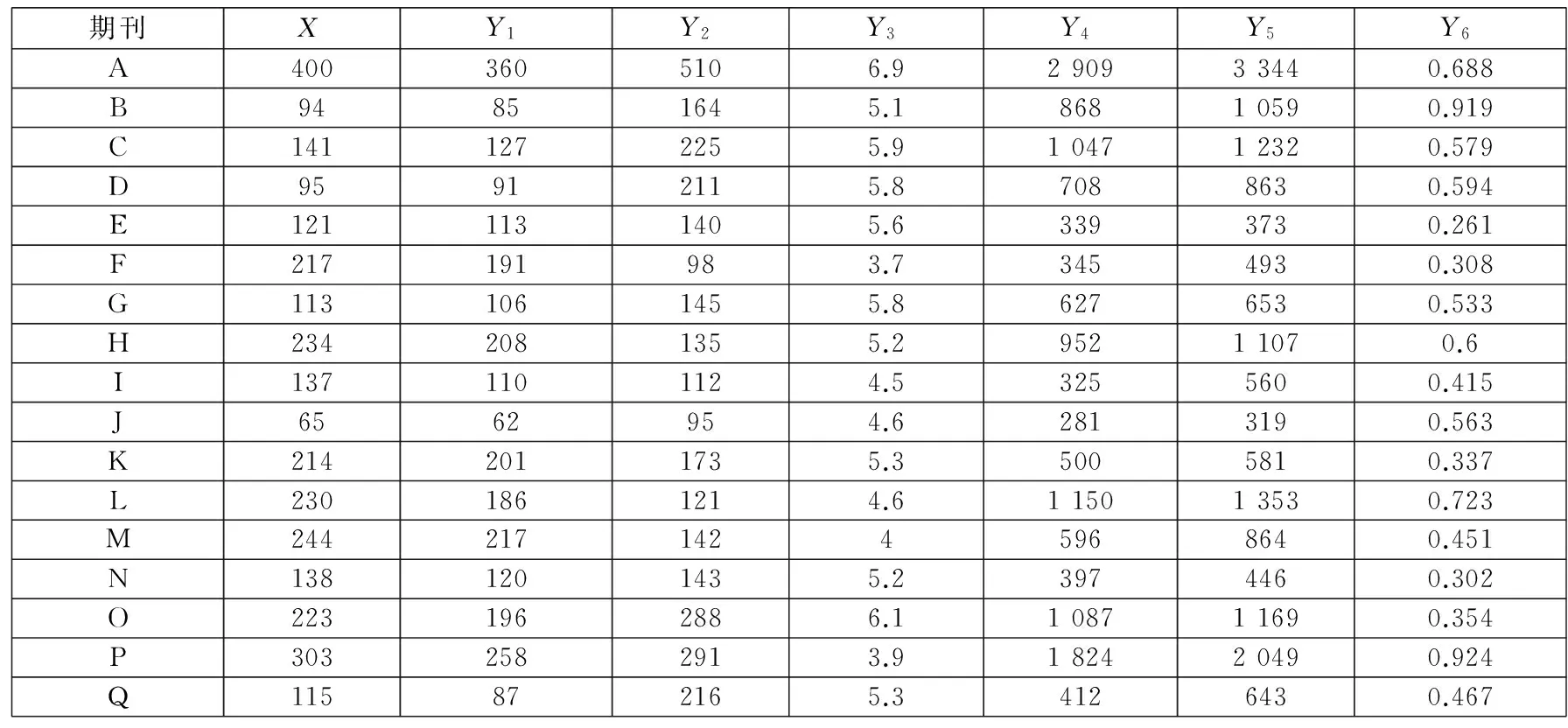
表1　2014年17种期刊的相关数据

3.3期刊评价结果

首先，考虑在两种指标集里，假设“影响因子”指标在期刊评价中相对来说更加容易被业内专家认可和重视，而“基金论文”指标则重视程度相对来说较低，其余产出指标的重视程度应该介于两者之间，没有明显区别. 根据这种决策偏好，构建下列DEA/AR模型

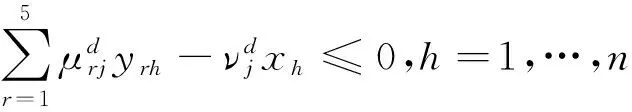
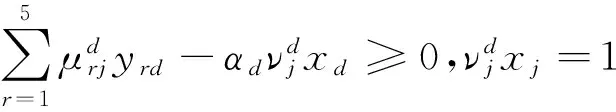
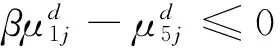
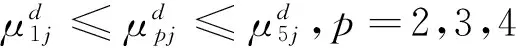
(9)

这里的β是常数，根据决策偏好设定. 本文分别选取β=1,2,3,4,5，分析在这5种情况下17种期刊的评价结果，进而总结出他们在2014年的总体状况.

其次，根据DEA/AR博弈交叉效率算法，设定计算精度ε=10-4，计算2014年17种样本期刊在两种指标集下的评价结果. 如图1所示，以期刊A在两种指标集下、偏好水平β=1为例，可以发现DEA/AR博弈交叉效率算法在不同指标集下都是收敛的. 实际上，不仅期刊A在这种情况下是收敛的，所有样本期刊在两种指标集下、不同的偏好水平内都是收敛的，这说明了算法的有效性.

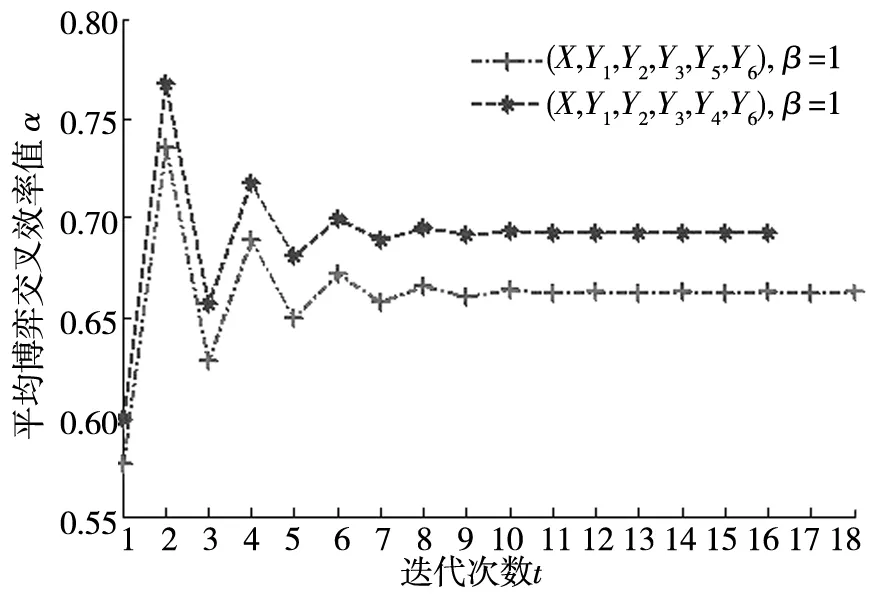
图1　期刊A在两种指标集下β=1时的博弈过程

如表2所示，在指标集(X,Y1,Y2,Y3,Y4,Y6)下，从纵向来看，为便于说明，本文按照评价值区间[0.8，1]和[0，0.8)将样本期刊划分出两个梯队，落入到两个区间的期刊数量分别为4个和13个. 第一梯队包含的期刊有B、C、D和J，其余的期刊都属于第二梯队. 值得注意的是，以期刊A为代表的一类期刊，在行业内具有很高的影响力，但是此次评价结果却不是很理想. 虽然期刊A每一项产出都比第一梯队的期刊C、D和J优秀的多，但是其评价值却远低于期刊C、D和J. 这主要是由于期刊A的刊文量(即投入项“来源文献量”)是所有样本期刊中最高的，大大拉低了其最终的评价值. 这种现象应当引起这类期刊管理者的重视. 在今后的期刊管理工作中，不仅需要关注提高各项产出水平，同时也要注意控制期刊的刊文量，争取能够用较小的刊文量取得较大的行业影响力，进而保证期刊的办刊质量.

从横向来看，随着对“影响因子”指标偏好程度的增加(β值由1逐渐增大到5)，各种期刊的评价值呈现降低(如期刊A和C)、不变(如期刊B和D)和增加(如期刊I和J)3种情况. 这表明指标权重的偏好信息会影响到期刊的评价结果，且在这种影响下所有可能的变化情况都会出现. 因此，在基于DEA/AR方法开展期刊评价工作时，在权重偏好的设定上需要慎重和符合实际.

如表3所示，在指标集(X,Y1,Y2,Y3,Y5,Y6)下，与指标集(X,Y1,Y2,Y3,Y4,Y6)相比，这里的期刊评价结果考虑到了自引频次的影响. 与表2结果相比，可以发现部分期刊在不同偏好水平下的评价值都相应地有所提高，如期刊I、M和Q，这说明了他们的自引频次相对其他期刊较高，需要注意适度控制自引频次. 反之，则自引频次相对较低，期刊的刊文质量能够得到读者的肯定，如期刊A、C和G. 此外，还存在少数期刊在两者情况下效率变化不大，说明他们的自引频次基本较为合理，如期刊D和E.

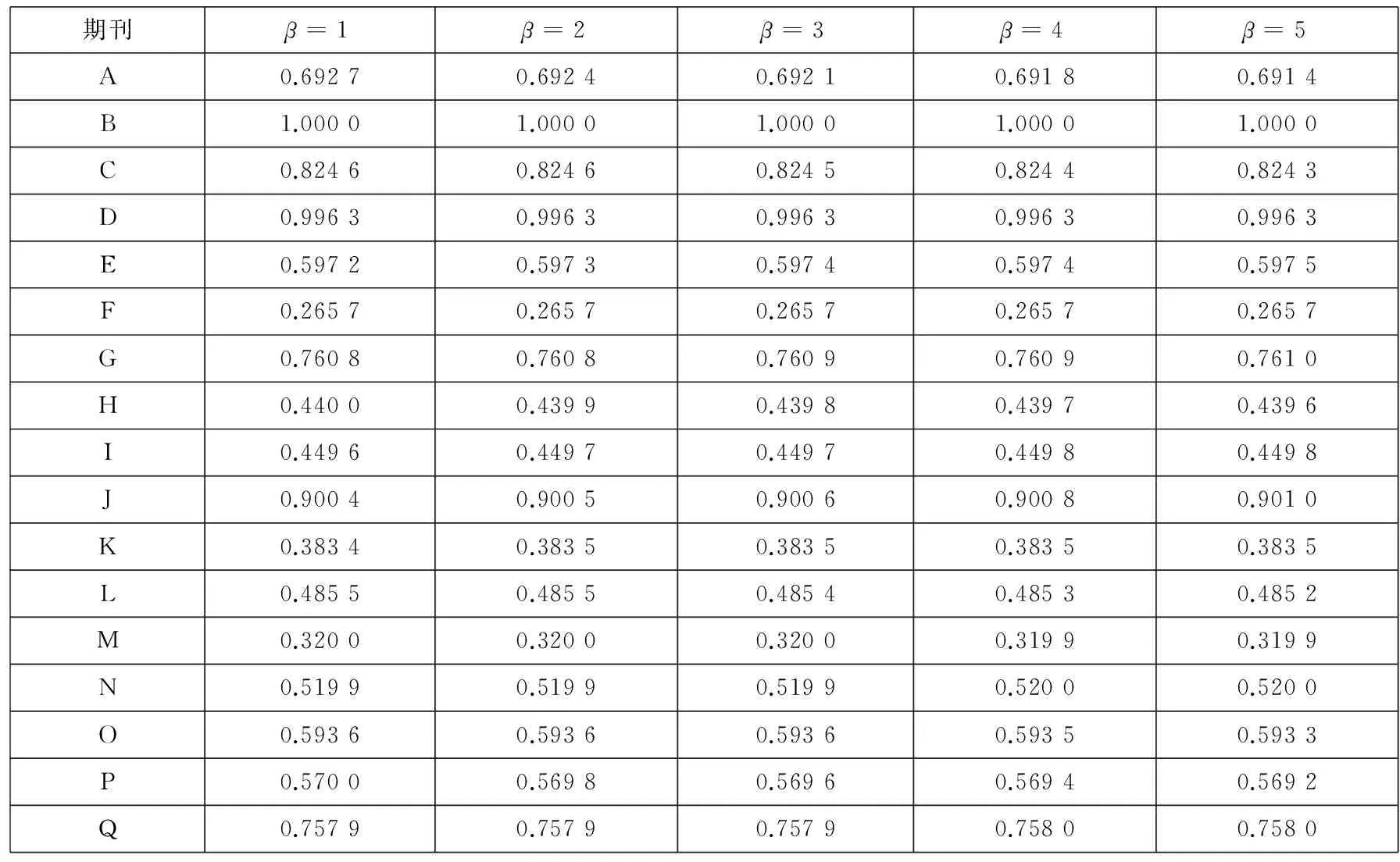
表2　(X,Y1,Y2,Y3,Y4,Y6)下期刊评价结果

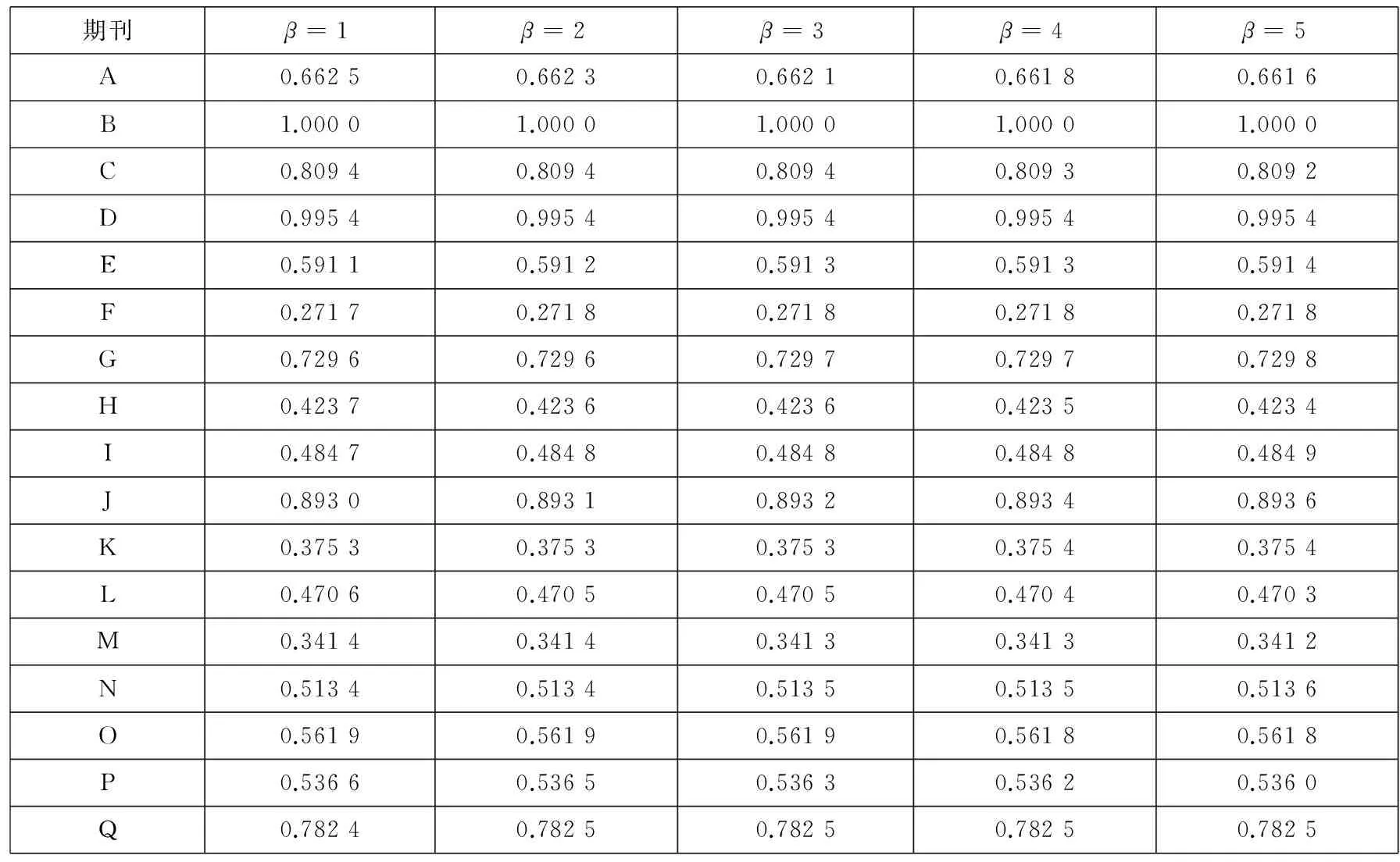
表3　(X,Y1,Y2,Y3,Y5,Y6)下期刊评价结果

4　结束语

考虑到传统期刊评价方法通常无法完全客观地评价具有多维指标的期刊投入产出绩效，因此本文将DEA方法引入到期刊评价工作中，通过将多维评价指标考虑到期刊评价过程中，根据期刊在多维指标下的实际表现，利用DEA方法为多维指标客观地赋予权重，最终得到一个更加全面和客观的评价结果.

具体来说，本文基于DEA/AR博弈交叉效率方法，从基金委管理科学部认定的30种管理科学重要学术期刊中，选取17种中国科技核心期刊作为样本展开分析，结果显示：

1)在行业内具有影响力的期刊未必一定能够获得较高的评价值. 这是由于DEA方法是从投入和产出两个角度共同考虑，研究DMU的相对效率. 部分有影响力的期刊，虽然有较高的产出水平，但是刊文量(投入)过高，导致相对评价值被拉低. 这要求期刊管理者应该综合考虑投入和产出两个方面，争取能够用较小的刊文量取得较大的行业影响力，以保证期刊的办刊质量.

2)指标权重的偏好信息会使得期刊的评价值出现增加、不变和减少三种情况. 因此，在基于DEA/AR方法开展期刊评价工作时，在权重偏好的设定上需要慎重和符合实际.

3)期刊在自引频次上存在着过度、适度和不足三种情况，需要期刊工作者在未来的工作中予以关注.

最后，本文的局限性和未来进一步的研究方向在：1)本文仅以2014年的数据计算说明，未能反映出期刊近年的变化趋势，难以体现出偶然因素的干扰；2)本文仅能对期刊作出评价，未能对期刊未来的绩效改进方向给出定量的建议.

[1]Garfield E. Citation indexes in sociological and historical research[J]. American Documentation, 1963, 14(4): 289-291.

[2]叶鹰. 一种学术排序新指数——f 指数探析[J]. 情报学报, 2009， (1): 142-149.

Ye Ying. F-index: A new indicator for academic ranking at all-round levels[J]. Journal of the China Society for Scientific and Technical Information, 2009， (1): 142-149. (in Chinese)

[3]俞立平, 姜春林. 学术期刊评价的视角、基本问题与发展展望[J]. 情报杂志, 2013, 32(5): 110-114.

Yu Liping, Jiang Chunlin. Visual angles, problems and trend in academic journal evaluation[J]. Journal of Intelligence, 2013, 32(5): 110-114. (in Chinese)

[4]Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units[J]. European Journal of Operational Research, 1978, 2(6): 429-444.

[5]Cook W D, Seiford L M. Data envelopment analysis (DEA)-Thirty years on[J]. European Journal of Operational Research, 2009, 192(1): 1-17.

[6]宋马林, 吴杰, 曹秀芬. 环境效率评价方法的统计属性分析及其实例[J]. 管理科学学报, 2013, 16(7): 45-54.

Song Malin, Wu Jie, Cao Xiufen. Analysis of statistical properties of environmental efficiency evaluation and its illustrations[J]. Journal of Management Sciences in China, 2013, 16(7): 45-54. (in Chinese)

[7]雷西洋, 王金年, 李勇军, 等. 基于集中式模型的我国各地区及三大产业的DEA效率评价[J]. 系统工程理论与实践, 2014, 34(12): 3167-3174.

Lei Xiyang, Wang Jinnian, Li Yongjun, et al. Measuring the DEA efficiencies of regions and their three major properties in China based on centralized model[J]. Systems Engineering: Theory & Practice, 2014, 34(12): 3167-3174. (in Chinese)

[8]李平, 曾勇, 朱晓琳. 中国银行业改革对中资银行效率变化的影响[J]. 管理科学学报, 2013, 16(8): 47-53.

Li Ping, Zeng Yong, Zhu Xiaolin. Impact of the reform of China’s banking sector on the changes in efficiency of Chinese banks[J]. Journal of Management Sciences in China, 2013, 16(8): 47-53. (in Chinese)

[9]Sexton T R, Silkman R H, Hogan A J. Data envelopment analysis: Critique and extensions[J]. New Directions for Program Evaluation, 1986, 1986(32): 73-105.

[10]Doyle J, Green R. Efficiency and cross-efficiency in DEA: Derivations, meanings and uses[J]. Journal of the Operations Research Society, 1994, (45): 567-578.

[11]吴杰. 数据包络分析(DEA)的交叉效率研究——基于博弈理论的效率评估方法[D]. 合肥: 中国科学技术大学出版社, 2008.

Wu Jie. Researches on cross efficiency of data envelopment analysis (DEA): The efficiency evaluation method based on game theory[D]. Hefei: Press of University of Science and Technology of China, 2008. (in Chinese)

[12]Liang L, Wu J, Cook W D, et al. The DEA game cross efficiency model and its Nash equilibrium[J]. Operations Research, 2008, 56(5): 1278-1288.

[13]Thompson R G, Singleton F D, Thrall R M, et al. Comparative site evaluations for locating a high energy physics lab in Texas[J]. Interfaces, 1986, 16: 35-49.

[14]Vinkler P. Evaluation of some methods for the relative assessment of scientific publications[J]. Scientometrics, 1986, 10(3): 157-177.

[15]Braun T, Glänzel W. A topographical approach to world publication output and performance in the sciences, 1981-1985[J]. Scientometrics, 1990, 19(3): 159-165.

[16]Moed H F, De Bruin R E, Van Leeuwen T N. New bibliometric tools for the assessment of national research performance: Database description, overview of indicators and first applications[J]. Scientometrics, 1995, 33(3): 381-422.

[17]Hirsch J E. An index to quantify an individual’s scientific research output[J]. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(46): 16569-16572.

[18]Bergstrom C T, West J D, Wiseman M A. The eigenfactor metrics[J]. The Journal of Neuroscience, 2008, 28(45): 11433-11434.

[19]Markpin T, Boonradsamee B, Ruksinsut K, et al. Article-count impact factor of materials science journals in SCI database[J]. Scientometrics, 2008, 75(2): 251-261.

[20]王小唯, 杨波, 潘启树. 科技期刊质量评估的二次相对评价方法[J]. 编辑学报, 2003, 15(3): 231-232.

Wang Xiaowei, Yang Bo, Pan Qishu. Secondary relative quality evaluation for sci-tech periodical publications[J]. Acta Editologica, 2003, 15(3): 231-232. (in Chinese)

[21]庞景安, 张玉华. 中国科技期刊综合评价指标体系的研究[J]. 中国科技期刊研究, 2000, 11(4): 217-219.

Pang Jingan, Zhang Yuhua. Study on the comprehensive evaluation index system of Chinese scientific and technical journals[J]. Chinese Journal of Scientific and Technical Periodicals, 2000, 11(4): 217-219. (in Chinese)

[22]俞立平, 潘云涛, 武夷山. 基于结构方程的学术期刊评价研究[J]. 情报学报, 2010, 29(1): 136-141.

Yu Liping, Pan Yuntao, Wu Yishan. Research on academic journal evaluation based on structural equation modeling[J]. Journal of the China Society for Scientific and Technical Information, 2010, 29(1): 136-141. (in Chinese)

[23]Yue W, Wilson C S. Measuring the citation impact of research journals in clinical neurology: A structural equation modelling analysis[J]. Scientometrics, 2004, 60(3): 317-332.

[24]邱均平, 张荣, 赵蓉英. 期刊评价指标体系及定量方法研究[J]. 现代图书情报技术, 2004, (7): 23-26.

Qiu Junping, Zhang Rong, Zhao Rongying. Study on the evaluation index system and methods for journal evaluation[J]. New Technology of Library and Information Service, 2004, (7): 23-26. (in Chinese)

[25]陈汉忠. 主成分分析在科技期刊评价中的应用[J]. 中国科技期刊研究, 2004, 15(6): 658-660.

Chen Hanzhong. An application of principal component analysis in the evaluation of scientific and technical journals[J]. Chinese Journal of Scientific and Technical Periodicals, 2004, 15(6): 658-660. (in Chinese)

[26]Charnes A, Cooper W W. Programming with linear fractional functions[J]. Naval Research Logistics Quarterly, 1962, (9): 181-185.

[27]Hughes A, Yaisawarng S. Sensitivity and dimensionality tests of DEA efficiency scores[J]. European Journal of Operational Research, 2004, 154(2): 410-422.

[28]Jenkins L, Anderson M. A multivariate statistical approach to reducing the number of variables in data envelopment analysis[J]. European Journal of Operation Research, 2003, 147: 51-61.

[29]Friedman L, Sinuany-Stern Z. Combining ranking scales and selecting variables in the DEA context: The case of industrial branches[J]. Computers & Operations Research, 1998, 25(9): 781-791.

Academic journal evaluation based on DEA/AR game cross efficiency method

LILin1,2,HUANGHai-jun1,WANGShou-yang2

1.School of Economics and Management, Beihang University, Beijing 100191, China;2.Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China

Academic journal evaluation is one of the important issues in journal research field. Traditional methods of data envelopment analysis are based on self-evaluation when evaluating the performance of academic journals. Without peer-evaluation, the evaluation result might be easily exaggerated. This paper studies the problem under the non-cooperative game framework by using data envelopment analysis/assurance region (DEA/AR) game cross efficiency method, and 17 Chinese sci-tech core journals are selected as an illustrative example. The results show that: 1) Some academic journals with high industry influence have non-ideal evaluation results: although their outputs are ideal, their published papers are non-ideal. 2) The evaluation values of academic journals could be increasing, unchanged, decreasing with the change of the preference of index weights. 3) The self-citeing of journals have three cases: excessive, moderate and insufficient. The evaluation result can provide a powerful decision reference for journal assistants to improve the competitiveness of journals.

journal evaluation; data envelopment analysis; performance evaluation; non-cooperative game; assurance region

① 2015-04-23；

2015-07-17.

国家自然科学基金资助项目(71224001).

李琳(1979—)， 女， 山东泰安人， 博士生. Email: lilin@iss.ac.cn

C934

A

1007-9807(2016)04-0118-09